用途
推しポイント
- 機械学習もtidyに行いたい人向け
- 色々なアルゴリズムを並列して実施できる
- パッケージごとに異なる変数を使っているのを統合可能
主なことはRユーザのためのtidymodels[実践]入門に書いてます。
ここでは使ってみたのを書いておきます。
コード
手法
みんな大好きirisで分類を実施
library(tidyverse)
library(tidymodels)
df_raw <- iris |> tibble()
実行
RFモデルで品種予測させてみる
バリデーション作成
10-foldのCVを行う strataで品種を指定してバリデーションの偏りをなくす
cv_data <- df_raw |> vfold_cv(strata = Species,v=10)
処理の確認
cv_data
## # 10-fold cross-validation using stratification
## # A tibble: 10 × 2
## splits id
## <list> <chr>
## 1 <split [135/15]> Fold01
## 2 <split [135/15]> Fold02
## 3 <split [135/15]> Fold03
## 4 <split [135/15]> Fold04
## 5 <split [135/15]> Fold05
## 6 <split [135/15]> Fold06
## 7 <split [135/15]> Fold07
## 8 <split [135/15]> Fold08
## 9 <split [135/15]> Fold09
## 10 <split [135/15]> Fold10
cv_data$splits[[1]] |> assessment()
## # A tibble: 15 × 5
## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## <dbl> <dbl> <dbl> <dbl> <fct>
## 1 5.1 3.5 1.4 0.2 setosa
## 2 5.4 3.7 1.5 0.2 setosa
## 3 4.8 3 1.4 0.1 setosa
## 4 5.4 3.4 1.5 0.4 setosa
## 5 5.3 3.7 1.5 0.2 setosa
## 6 6.9 3.1 4.9 1.5 versicolor
## 7 5.7 2.8 4.5 1.3 versicolor
## 8 5.6 2.5 3.9 1.1 versicolor
## 9 6.7 3 5 1.7 versicolor
## 10 6.3 2.3 4.4 1.3 versicolor
## 11 6.3 3.3 6 2.5 virginica
## 12 6.9 3.2 5.7 2.3 virginica
## 13 6.4 2.8 5.6 2.2 virginica
## 14 6.3 2.8 5.1 1.5 virginica
## 15 6 3 4.8 1.8 virginica
前処理
何を予測させるかの指示と、正規化などの前処理をrecipeに指定
rec_base <- recipe(Species ~ ., data=df_raw) |> # ここではデータ全体を使って正規化する
step_normalize(all_numeric(), -all_outcomes())
処理の確認
rec_base |> prep() |> bake(new_data = NULL)
## # A tibble: 150 × 5
## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## <dbl> <dbl> <dbl> <dbl> <fct>
## 1 -0.898 1.02 -1.34 -1.31 setosa
## 2 -1.14 -0.132 -1.34 -1.31 setosa
## 3 -1.38 0.327 -1.39 -1.31 setosa
## 4 -1.50 0.0979 -1.28 -1.31 setosa
## 5 -1.02 1.25 -1.34 -1.31 setosa
## 6 -0.535 1.93 -1.17 -1.05 setosa
## 7 -1.50 0.786 -1.34 -1.18 setosa
## 8 -1.02 0.786 -1.28 -1.31 setosa
## 9 -1.74 -0.361 -1.34 -1.31 setosa
## 10 -1.14 0.0979 -1.28 -1.44 setosa
## # ℹ 140 more rows
モデル指定
ここではrangerパッケージを使ってRFを行う
mtryとmin_nは後でハイパラ探索するのでtune()とする。
ml_rf <- rand_forest(
mtry = tune(),
trees = 500,
min_n = tune()
) |>
set_mode("classification") |> # 分類モデルを指定
set_engine("ranger",importance = "impurity") # importanceを出すように指定
ワークフロー
recipeをモデルの一連の解析を一度にできるようにワークフローを設定 無しでもできる。
wf_base <- workflow() |>
add_recipe(rec_base) |>
add_model(ml_rf)
ハイパラ探索
検証したいレンジを指定して実施
# レンジの指定。適時調整
param_rf <- list(min_n(range=c(1,5)),
mtry(range = c(1,4))
) |>
dials::parameters()
# グリッドサーチでの探索点を指定
set.seed(11)
grid_range <- param_rf |>
dials::grid_random(size=10) # 今回はパラメータ探索幅が少ないので10個も多分出ない
# 探索実施
res_grid <- wf_base |>
tune_grid(resamples = cv_data,
grid = grid_range,
# control = control_grid(save_pred = TRUE), # 予測値を残すか
metrics = yardstick::metric_set(accuracy,roc_auc)) # 判定したいスコアを指定
パラメータ探索の結果
res_grid |> show_best(metric = "accuracy")
## # A tibble: 5 × 8
## mtry min_n .metric .estimator mean n std_err .config
## <int> <int> <chr> <chr> <dbl> <int> <dbl> <chr>
## 1 2 5 accuracy multiclass 0.967 10 0.0111 Preprocessor1_Model05
## 2 3 4 accuracy multiclass 0.967 10 0.0111 Preprocessor1_Model07
## 3 4 5 accuracy multiclass 0.967 10 0.0111 Preprocessor1_Model08
## 4 3 5 accuracy multiclass 0.967 10 0.0111 Preprocessor1_Model09
## 5 3 3 accuracy multiclass 0.96 10 0.0147 Preprocessor1_Model10
res_grid |> autoplot()

説明変数は3つがよさそう
モデル設定と更新
# 結果確認
res_grid |> collect_metrics()
## # A tibble: 20 × 8
## mtry min_n .metric .estimator mean n std_err .config
## <int> <int> <chr> <chr> <dbl> <int> <dbl> <chr>
## 1 1 2 accuracy multiclass 0.947 10 0.0133 Preprocessor1_Model01
## 2 1 2 roc_auc hand_till 0.993 10 0.00358 Preprocessor1_Model01
## 3 3 2 accuracy multiclass 0.953 10 0.0174 Preprocessor1_Model02
## 4 3 2 roc_auc hand_till 0.996 10 0.00285 Preprocessor1_Model02
## 5 3 1 accuracy multiclass 0.953 10 0.0174 Preprocessor1_Model03
## 6 3 1 roc_auc hand_till 0.996 10 0.00285 Preprocessor1_Model03
## 7 1 1 accuracy multiclass 0.947 10 0.0133 Preprocessor1_Model04
## 8 1 1 roc_auc hand_till 0.993 10 0.00358 Preprocessor1_Model04
## 9 2 5 accuracy multiclass 0.967 10 0.0111 Preprocessor1_Model05
## 10 2 5 roc_auc hand_till 0.995 10 0.00295 Preprocessor1_Model05
## 11 1 4 accuracy multiclass 0.947 10 0.0133 Preprocessor1_Model06
## 12 1 4 roc_auc hand_till 0.993 10 0.00358 Preprocessor1_Model06
## 13 3 4 accuracy multiclass 0.967 10 0.0111 Preprocessor1_Model07
## 14 3 4 roc_auc hand_till 0.996 10 0.00285 Preprocessor1_Model07
## 15 4 5 accuracy multiclass 0.967 10 0.0111 Preprocessor1_Model08
## 16 4 5 roc_auc hand_till 0.996 10 0.00285 Preprocessor1_Model08
## 17 3 5 accuracy multiclass 0.967 10 0.0111 Preprocessor1_Model09
## 18 3 5 roc_auc hand_till 0.996 10 0.00285 Preprocessor1_Model09
## 19 3 3 accuracy multiclass 0.96 10 0.0147 Preprocessor1_Model10
## 20 3 3 roc_auc hand_till 0.996 10 0.00285 Preprocessor1_Model10
# accuracyが一番いいのを取ってくる
best_param <-
res_grid |>
select_best("accuracy")
# いいハイパラでワークフローの更新
wf_best <- wf_base |>
finalize_workflow(best_param)
適用
res_best <- wf_best |>
fit_resamples(resamples = cv_data, control = control_resamples(save_pred = TRUE))
collect_metrics(res_best)
## # A tibble: 2 × 6
## .metric .estimator mean n std_err .config
## <chr> <chr> <dbl> <int> <dbl> <chr>
## 1 accuracy multiclass 0.967 10 0.0111 Preprocessor1_Model1
## 2 roc_auc hand_till 0.995 10 0.00295 Preprocessor1_Model1
df_pred <- augment(res_best)
可視化
df_pred |>
ggplot(aes(x=Species, y=.pred_class)) +
geom_jitter(width = 0.2,height = 0.2)
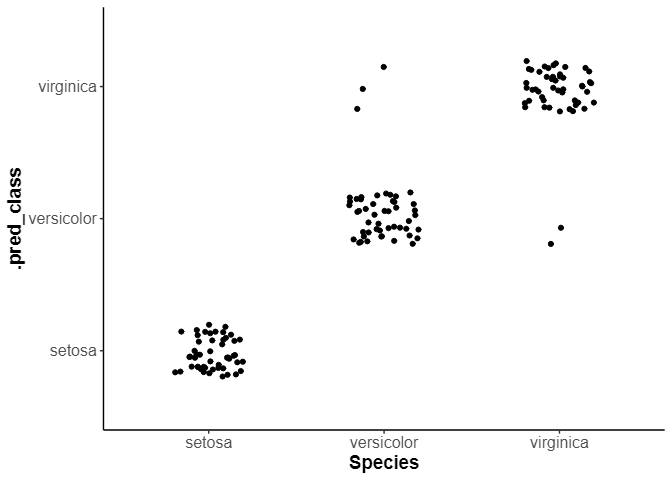
混同行列
res_best |> collect_predictions() |> conf_mat(Species,.pred_class) |> autoplot(type="heatmap")
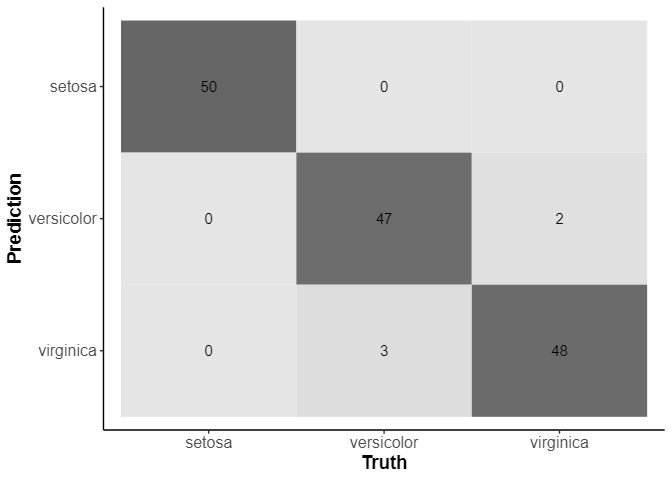
ROC_curve
res_best |> collect_predictions() |> roc_curve(Species, .pred_setosa:.pred_virginica) |> autoplot()
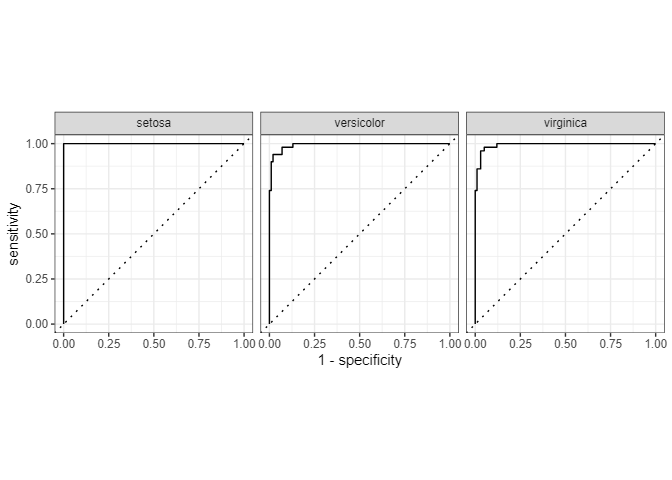
setosaは楽勝といういつもの流れ
重要度
各cvのモデルの重要度を取得
# CV
fit_eachcv <- function(split_data) {
wf_best |> fit(analysis(split_data)) |>
extract_fit_engine() |> importance() |> as.table()
}
cv_fit <- cv_data |> mutate(importance = map_dfr(splits, fit_eachcv)) |> pull(importance)
cv_fit |> as.matrix() |> t() |> as.data.frame() |>
rownames_to_column() |>
pivot_longer(cols = -rowname) |>
ggplot(aes(x=reorder(rowname,value,FUN = mean),y=value)) +
stat_summary(geom = "bar", fun=mean,position = "dodge") +
stat_summary(fun.min = function(x) mean(x) - sd(x), fun.max = function(x) mean(x) + sd(x),geom = "errorbar",position = "dodge", width = 0.3, size = 1) +
labs(x=NULL) +
coord_flip()
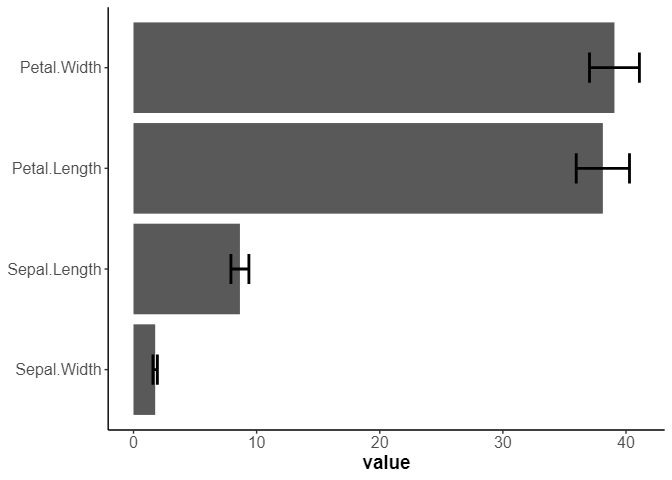
2強状態
三角図で確率を示す
(執筆時点ではggternがCRANから外れていたので、こちらを参考にした。戻っているのでggternを使った方が楽。)
色は正解ラベル
gg_tripred <- function(df_pred) {
axis_lab <- c("pred_setosa","pred_versicolor","pred_virginica")
# 軸目盛の位置を指定
axis_vals <- seq(from = 0, to = 1, by = 0.1)
# 枠線用の値を作成
ternary_axis_df <- tibble::tibble(
y_1_start = c(0.5, 0, 1), # 始点のx軸の値
y_2_start = c(0.5*sqrt(3), 0, 0), # 始点のy軸の値
y_1_end = c(0, 1, 0.5), # 終点のx軸の値
y_2_end = c(0, 0, 0.5*sqrt(3)), # 終点のy軸の値
axis = c("x_1", "x_2", "x_3") # 元の軸
)
# グリッド線用の値を作成
ternary_grid_df <- tibble::tibble(
y_1_start = c(
0.5 * axis_vals,
axis_vals,
0.5 * axis_vals + 0.5
), # 始点のx軸の値
y_2_start = c(
sqrt(3) * 0.5 * axis_vals,
rep(0, times = length(axis_vals)),
sqrt(3) * 0.5 * (1 - axis_vals)
), # 始点のy軸の値
y_1_end = c(
axis_vals,
0.5 * axis_vals + 0.5,
0.5 * rev(axis_vals)
), # 終点のx軸の値
y_2_end = c(
rep(0, times = length(axis_vals)),
sqrt(3) * 0.5 * (1 - axis_vals),
sqrt(3) * 0.5 * rev(axis_vals)
), # 終点のy軸の値
axis = c("x_1", "x_2", "x_3") |>
rep(each = length(axis_vals)) # 元の軸
)
# 軸ラベル用の値を作成
ternary_axislabel_df <- tibble::tibble(
y_1 = c(0.25, 0.5, 0.75), # x軸の値
y_2 = c(0.25*sqrt(3), 0, 0.25*sqrt(3)), # y軸の値
label = axis_lab, # 軸ラベル
h = c(1.5, 0.5, -0.5), # 水平方向の調整用の値
v = c(0.5, 2.5, 0.5), # 垂直方向の調整用の値
axis = c("x_1", "x_2", "x_3") # 元の軸
)
# 軸目盛ラベル用の値を作成
ternary_ticklabel_df <- tibble::tibble(
y_1 = c(
0.5 * axis_vals,
axis_vals,
0.5 * axis_vals + 0.5
), # x軸の値
y_2 = c(
sqrt(3) * 0.5 * axis_vals,
rep(0, times = length(axis_vals)),
sqrt(3) * 0.5 * (1 - axis_vals)
), # y軸の値
label = c(
rev(axis_vals),
axis_vals,
rev(axis_vals)
), # 軸目盛ラベル
h = c(
rep(1.5, times = length(axis_vals)),
rep(1.5, times = length(axis_vals)),
rep(-0.5, times = length(axis_vals))
), # 水平方向の調整用の値
v = c(
rep(0.5, times = length(axis_vals)),
rep(0.5, times = length(axis_vals)),
rep(0.5, times = length(axis_vals))
), # 垂直方向の調整用の値
angle = c(
rep(-60, times = length(axis_vals)),
rep(60, times = length(axis_vals)),
rep(0, times = length(axis_vals))
), # ラベルの表示角度
axis = c("x_1", "x_2", "x_3") |>
rep(each = length(axis_vals)) # 元の軸
)
# 三角座標に変換して格納
data_df <- df_pred |>
mutate(
x_1 = .pred_setosa, # 元のx軸の値
x_2 = .pred_versicolor, # 元のy軸の値
x_3 = .pred_virginica, # 元のz軸の値
y_1 = x_2 + 0.5 * x_3, # 変換後のx軸の値
y_2 = sqrt(3) * 0.5 * x_3, # 変換後のy軸の値
label = str_c("(", round(x_1, 2), ", ", round(x_2, 2), ", ", round(x_3, 2), ")")
)
# 三角図の各軸を可視化
ggplot() +
geom_segment(data = ternary_axis_df,
mapping = aes(x = y_1_start, y = y_2_start, xend = y_1_end, yend = y_2_end),
color = "gray50") + # 三角図の枠線
geom_segment(data = ternary_grid_df,
mapping = aes(x = y_1_start, y = y_2_start, xend = y_1_end, yend = y_2_end),
linetype = "dashed") + # 三角図のグリッド線
geom_text(data = ternary_ticklabel_df,
mapping = aes(x = y_1, y = y_2, label = label, hjust = h, vjust = v, angle = angle)) + # 三角図の軸目盛ラベル
geom_text(data = ternary_axislabel_df,
mapping = aes(x = y_1, y = y_2, label = label, hjust = h, vjust = v),
parse = TRUE, size = 6) + # 三角図の軸ラベル
geom_point(data = data_df,
mapping = aes(x = y_1, y = y_2, color=Species),
size = 3) + # 観測データ
scale_x_continuous(breaks = c(0, 0.5, 1), labels = NULL) + # x軸
scale_y_continuous(breaks = c(0, 0.25*sqrt(3), 0.5*sqrt(3)), labels = NULL) + # y軸
scale_color_brewer(palette = "Set2") +
coord_fixed(ratio = 1, clip = "off") + # アスペクト比
theme(
axis.ticks = element_blank(), # 目盛の指示線
panel.grid.minor = element_blank(), # 補助目盛のグリッド線
legend.position = c(0.8,0.8) # 凡例の位置
) + # 図の体裁
labs(x = "", y = "") +
theme(
axis.line = element_blank()
)
}
gg_tripred(df_pred = df_pred)
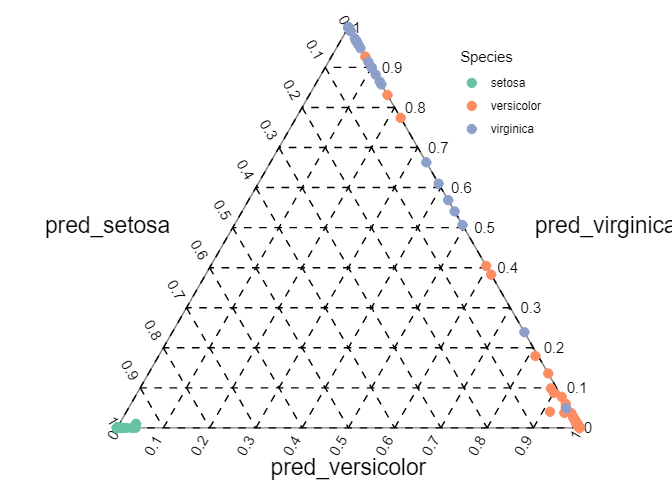
setosaは楽勝 自信もって間違えている点もあるので、かなり難しいか実データなら誤ラベルも考えられる
備考
最初に話した本が一番です。
またここで行っているCVはモデルの汎化性能を評価する交差検証であり、ハイパラ探索は一番当てられたものを釣ってきています。
つまり、ハイパラ探索をやらずに出しているものに比べたら予測がfitするので、モデルの信頼度が高くできる一方で、未知なものへの予測の保証はあまりありません。大切な特徴量を分析する目的で利用しています。