Stan Advent Boot Camp 第11日目 : stanで混合分布モデル(潜在クラス分析)をやってみる

stanアドカレ11日目の記事です。

昨日はdastatisの記事でした(本当はstan boot advent campは10日で終わる予定だったのですが、書きたかったので追加しました)

今日はstanで混合分布モデルを推定する方法についてです。

はじめに

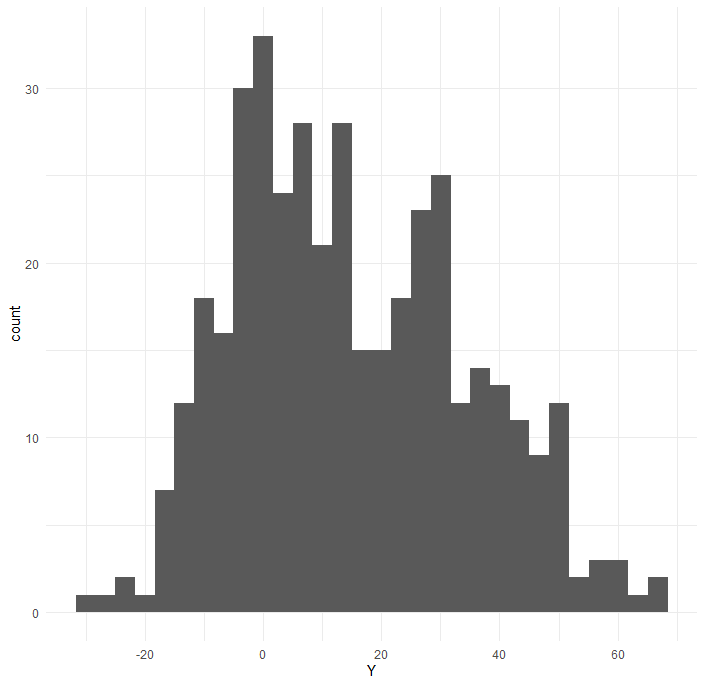
何かしらのデータを400個取得したらこんな、ヒストグラムになりました。

取得したデータの生成モデルを考えるとしましょう。

一見、正規分布っぽい様に見えるような、見えないような....

単峰ではなく多峰の様に見えます

どういう分布で近似するのが良いのでしょうか。

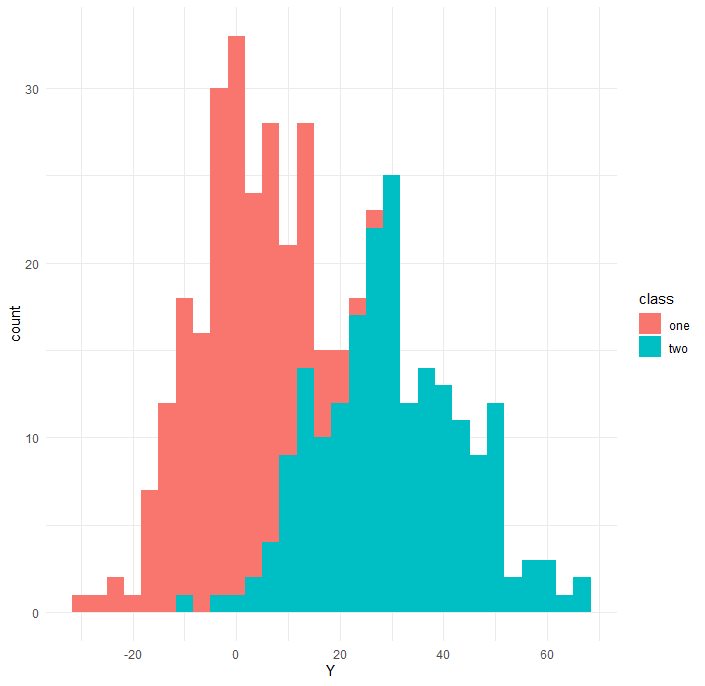
種明かしすると、このデータは二つの異なる分布から生成されています。

クラスがoneかtwoかで異なるパラメータを持つ正規分布から生成されています。

手元にクラス情報があれば、クラス別に階層化させればいいですが、今回はありません。

そうしたときに、混合分布モデルを使うことが出来ます。

混合分布モデル(潜在クラスモデル)とは

データの背後に潜在的な複数の確率分布を仮定し、それぞれの確率分布のに所属している確率を推定するモデルです

離散有限混合分布モデル(discrete finite mixture model)のことを潜在クラス分析(Latent Class Analysis:LCA)というらしい(引用)

教師無し学習のクラスタリングに似ており、K-meansなどのデータを顕在的にクラスに分けるクラスタリングをハードクラスタリング(Aはクラス1だ!!)、混合分布モデルの様に潜在的に各クラスに所属している確率を推定するクラスタリングをソフトクラスタリング(Aはクラス1に属している確率が80%!!)といいます。

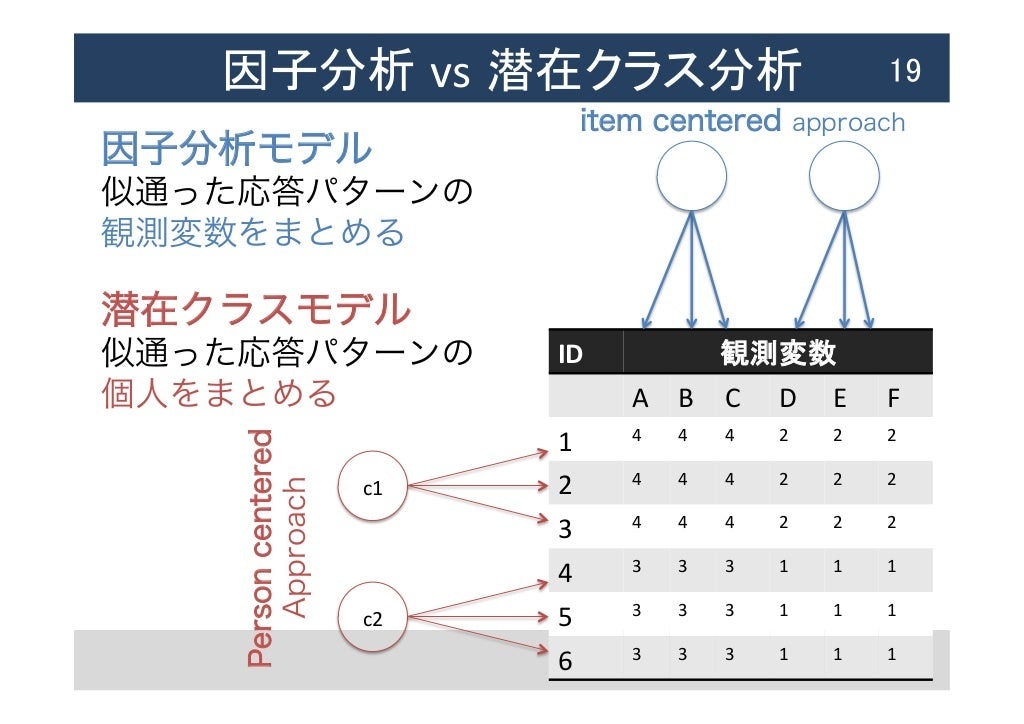
因子分析の対象(人)版みたいなもので、因子分析は類似の観測変数(尺度項目など)をまとめ上げる一方、

潜在クラスモデルは類似の対象(参加者など)をまとめるイメージです。

※人を対象にした因子分析のテクニックもあるらしいです

引用：https://www.slideshare.net/yoshitaket/ss-56356699

そういう意味で、潜在クラスモデルはセグメンテーションといった消費者の異質性を解釈する手法としても用いられたりします。

クラス数の決定に関しては、AICなどの情報量規準から決定することが一般的です。

stanのリファレンスマニュアルに沿って説明します

K個の正規分布があり、それぞれのパラメータを$\mu_k,\sigma_k$とします

K個の正規分布を割合$\theta_k$で混合させるとします。各成分割合は非負の値($\theta_k\geq0$)をとり、確率なので合計が1になります($\sum_{k=1}^K\theta_k=1$)。例えば二つの正規分布を仮定しており(K=2)、$\theta_1=0.2$なら$\theta_2=0.8$となります。

混合成分$z_n$はパラメータ$\theta$をもつカテゴリカル分布に従うとします
$$
z_n\sim {\rm Categorical}(\theta)
$$
変数$y_n$は混合成分$z_n$のパラメータに従って分布します
$$
y_n\sim{\rm Normal}(\mu_{z[n]},\sigma_{z[n]})
$$
しかし、離散パラメータ$z_n$をstanでは直接扱うことが出来ないため、総和によって離散パラメータをモデルから消去することで実装します。YがK個の正規分布の混合分布で、各成分$\theta_k$で混合される場合は次式で表現されます
$$
p_Y(y|\theta,\mu,\sigma)=\sum_{k=1}^K\theta_k {\rm Normal}(\mu_k,\sigma_k)
$$
変数$y$は成分$\theta_k$で重みづけられた正規乱数の総和によって生成されるというイメージですかね。

二つの正規分布(K=2)を仮定すると、以下のようになります
$$
p_Y(y|\theta,\mu,\sigma)=\sum_{k=1}^2\theta_k {\rm Normal}(\mu_k,\sigma_k)\
=(\theta_1 {\rm Normal}(\mu_1,\sigma_1)+\theta_2 {\rm Normal}(\mu_2,\sigma_2))
$$

Rとstanで推定

データ

#パッケージ
library(tidyverse)
library(rstan)
#おまじない
options(mc.cores = parallel::detectCores())
rstan_options(auto_write = TRUE)
#ggplotのテーマ指定
theme_set(theme_minimal()) 

#疑似データの生成
n <- 200
mu1 <- 0
sig1 <- 10
mu2 <- 30
sig2 <- 15

set.seed(42) #生命、宇宙、そして万物についての究極の疑問の答え
one <- rnorm(n,mu1,sig1)
two <- rnorm(n,mu2,sig2)
df <- data.frame(Y = c(one,two),
           class = rep(c("s1","s2"),each=n)) %>% 
  rowid_to_column("id") 

stanコード

ソフトクラスタリングの良さみを知るために、データごとに各分布の所属確率を推定します

data {
  int<lower=1> K;          // 混合成分の数
  int<lower=1> N;          // データ点の数
  real y[N];               // 観測値
}

parameters {
  simplex[K] theta[N];        // 混合確率(simplexによって合計が1になる)
  ordered[K] mu;              // 混合成分の位置(順序型にしておくと収束しやすい)
  real<lower=0> sigma[K];  // 混合成分のスケール
}

transformed parameters{
  vector[K] lp[N];              // 成分密度の対数の一時変数
  for (n in 1:N) {
    for (k in 1:K) {
      lp[n,k] = log(theta[n,k])+ normal_lpdf(y[n]|mu[k],sigma[k]);
    }
  }
}

model{
  for(n in 1:N){
    target+=log_sum_exp(lp[n]); //log_sum_expでアンダー/オーバーフローを防ぐ
  }
  sigma ~ cauchy(0,2.5);
  mu ~ normal(0,10);
}

generated quantities{
  real log_lik[N];
  vector[K] p[N];
  int<lower=1,upper=K> s[N];
  real pred_y[N];
  
  for(n in 1:N){
    log_lik[n] = log_sum_exp(lp[n]); //対数尤度の計算
    p[n] = softmax(lp[n]); //各観測地の成分割合をソフトマックス関数で0~1に戻す
    s[n] = categorical_rng(p[n]); //カテゴリカル分布からクラスを生成
    pred_y[n] = normal_rng(mu[s[n]],sigma[s[n]]); 
  }
}

基本的に最初の説明で書いてある通りです

• thetaはsimplex型(非負で総和が1)にします

log_sum_exp()

尤度の計算では、対数スケールに変換して計算することが多い(今回もそう)です。混合分布モデルでは、複数の分布に対するそれぞれの成分割合を算出する必要があり、対数をとった尤度を使って計算すると、アンダーフローする可能性があります。そこで対数確率を指数関数で一度戻して和をとり、もう一度対数変換するというテクニックを使うことで推定精度を保っているそうです。

ターゲット記法(target+=)で尤度を足し上げます

• 混合ガウス分布とlogsumexp - Qiita
• 対数で確率を扱う話 - HackMD

muはordered型がいい

stanにおけるordered型は、パラメータに順序関係を持たせています。stanを使って混合分布モデルを推定させようとすると、ラベルスイッチングや多峰性の問題で、うまく収束しないことがあります。1パラならorderedにしたほうがいいと思います。

推定

dataset <- list(K = 2, #潜在クラスの数
                y = df$Y,
                N = nrow(df))

# stanで推定
fit <- stan(file = "latent_class.stan",  #ここは自分で作ったコードにしてね♬
            data = dataset,
            seed = 42, #生命、宇宙、そして万物についての究極の疑問の答え
            iter = 5000,
            warmup = 2500,
            chain = 4)

推定結果

モデル評価(WAIC)

モデル
正規分布モデル	240006.6
混合分布モデル(2クラス)	3472.396
混合分布モデル(3クラス)	3481.733
混合分布モデル(4クラス)	3484.233

おぉーん...

答えは2なので、2クラスモデルについて結果を見ていきます

パラメータ

         mean se_mean   sd  2.5%   25%   50%   75% 97.5% n_eff Rhat
mu[1]     0.27    0.01 1.05 -1.70 -0.44  0.24  0.95  2.44  7536    1
mu[2]    28.87    0.02 1.58 25.73 27.84 28.90 29.95 31.87  6738    1
sigma[1] 10.28    0.01 0.78  8.87  9.74 10.24 10.77 11.99  8037    1
sigma[2] 15.28    0.02 1.17 13.20 14.47 15.20 16.02 17.79  6037    1

それぞれの真値について、mu1=0、mu2=30、sigma1=10、sigma2=15でした。

事後予測分布チェック

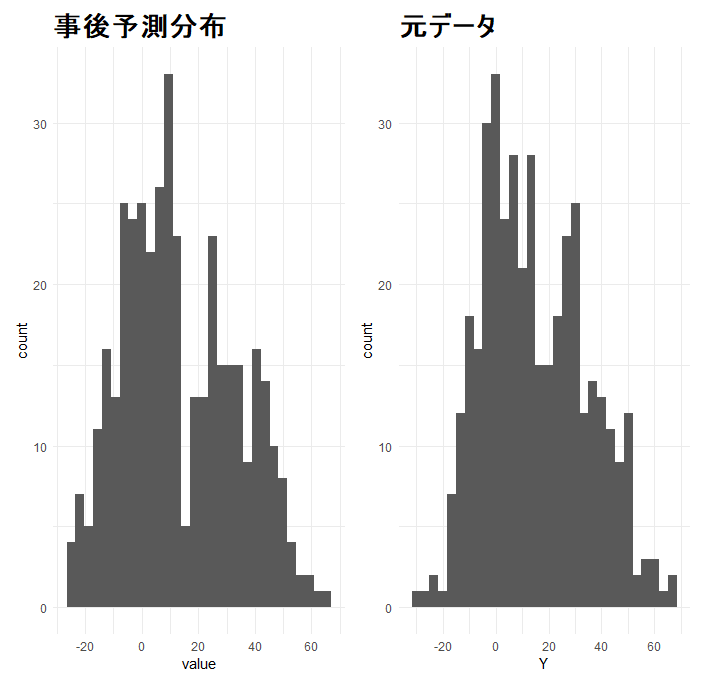
元データのヒストグラムとMCMCサンプルによる事後予測分布の確認

#元データの
hist <- df %>% 
  ggplot()+
  aes(x=Y)+
  geom_histogram()+
  scale_x_continuous(breaks = seq(-100,100,20))+
  ggtitle("元データ")+theme(plot.title = element_text(size = 20, face = "bold"))

# 事後予測分布
p_ph <- fit %>%
  rstan::extract() %$% pred_y  %>%
  data.frame() %>%
  as_tibble() %>%
  rowid_to_column("iter") %>%
  pivot_longer(-iter) %>%
  ランダムに400点だけ抜き出す
  sample_n(400) %>% 
  ggplot() +
  aes(x = value)+
  geom_histogram()+
  scale_x_continuous(breaks = seq(-100,100,20))+
  ggtitle("事後予測分布")+theme(plot.title = element_text(size = 20, face = "bold"))

library(patchwork)
p_ph+hist

左が事後予測分布、右が元データ

(???)「恐ろしく似たヒストグラム...俺でなきゃ(ry」

生成量による対象の所属クラス

折角、MCMCでソフトクラスタリングするなら、対象がクラスに所属している確率の分布を見たい

# 個人ごとの各クラス所属確率
lp <- fit %>%
  #generated quantitiesで算出した観測値ごとの各潜在クラスへの所属確率
  rstan::extract() %$% p %>%
  data.frame(p=.) %>% 
  as_tibble() %>% 
  rowid_to_column("iter") %>% 
  pivot_longer(-iter) %>% 
  mutate(id = str_split(name, pattern = "[.]", simplify = T)[, 2] %>% as.numeric(),
         class = str_c("s",str_split(name, pattern = "[.]", simplify = T)[, 3]))

疑似データから、適当にサンプルを抜き出し、クラス1(s1)に属する確率を算出

• id:18(答えはs1)は、値がとても小さいので、s1クラスに所属している確率が高いです
• id:240(答えはs2)は、二つの分布が比較的重なる部分にあるので、id:18よりも分布の幅が広くなっています
• id:342(答えはs2)は、全体のデータの中では比較的大きく、s1クラスの所属確率はとても小さいです

#id=18を例にコード
hist_18 <- 
  df %>% 
  ggplot()+
  aes(x=Y)+
  geom_histogram()+
  geom_vline(xintercept = filter(df,id==18)$Y,col="red",size=2)+
  scale_x_continuous(breaks = seq(-100,100,20))

# 18番目の人のデンシティプロット
dens_18 <- 
lp %>% 
  filter(id == 18) %>% 
  ggplot()+
  aes(x = prob,fill=class)+
  geom_density(aes())

library(patchwork)
hist_18+ggtitle("id:18,s1")+theme(plot.title = element_text(size = 20, face = "bold"))+dens_18

終わりに

stanをつかった混合分布モデルは推定がなかなか難しく、変分ベイズ法も視野に入れたほうがいいかもしれません(MCMCと結果が一致するか分からんので、それもあまりおすすめはしません)。あとは、潜在クラスを仮定するパラメータを増やすと収束しづらくなったりします(今年は、潜在クラスモデルをいじいじして半年溶けました)。この辺は、うまく推定するコツとかもっとあるかもしれないので、知ってる方いたら教えてください。

とはいえ、生成量を使うことでソフトクラスタリングを直感的にとらえることができて、僕は好きです

明日は、kameryon8さんの記事です。

参考文献

• HADで混合分布モデル・潜在クラス分析 | Sunny side up!
• 潜在クラス分析
• stanマニュアル
• 混合分布モデル・潜在クラス分析 - メモ