LoginSignup
3
4

More than 1 year has passed since last update.

@amutou

Arm CMSIS DSP_Lib FFT

Last updated at Posted at 2018-06-29

　STM32CubeMXで出力したときに一緒に出てくるDSPライブラリの中で、今回はFFTを試してみる。

環境

　STM32F405RG(Cortex-M4F) / 168MHz

基礎知識

　DSP_LibにはいくつかのFFTの種類があります。
　大きく分けて、実数のみを扱うRFFT(Real FFT)と、複素数を扱うCFFT(Complex FFT)の2種類です。さらに、各値をfloat32で計算するf32、各値を15bit固定小数点で扱うq15、各値を31bit固定小数点で扱うq31、の3種類で、計6種類のインターフェースになります。
　その他の関数もありますが、基本的に使わないので今回は無視します。

　CFFTの場合は16ポイントから4096ポイントまで、RFFTの場合は32ポイントから4096ポイントまでを処理できます。

その他

　q15/q31の使い方はf32とほぼ同様なので、今回は固定小数点は扱わないことにします。Cortex-M4FはFPUを内蔵しているので、固定小数点なら早い、floatは劇的に遅い、といったことはないはずです。

　処理時間のベンチマークのため、TIM2を使用しています。
　精度を要求しないのであればHAL_GetTickにより1msec単位での計測が可能ですが、今回はTIM2を使って1usec単位での計測を行いました(さらに精度を求めるなら11.9nsec単位まで計測できますが、今回はそこまでは求めないことにします)。

リンク/インクルード

　FFTの機能はバイナリで提供されているので、リンク時に追加する必要があります。
　MakefileのLIBSにDrivers/CMSIS/DSP/Lib/GCC/libarm_cortexM4lf_math.aを追加しておきます。

　CFFTを使う場合はDrivers/CMSIS/DSP/Include/arm_const_structs.hをインクルードします。
　RFFTを使う場合はDrivers/CMSIS/DSP/Include/arm_math.hをインクルードします。
　atm_math.hはarm_const_structs.hからインクルードされています。
　このインクルードを行う際にARMコアの種類を明示しておく必要があります。ということで#define ARM_MATH_CM4を定義した後にincludeを行います(使用するコアに合わせて修正してください)。

ソースコード

　とりあえずソースコードを貼り付けておきます。
　前半がCFFT、後半がRFFTの処理です。

static float32_t buff_C[4096 * 2]; // complex

uint16_t FFT_point = 0;
bool flag = true;

if (1 == sscanf(str, "CFFT %hu", &FFT_point))
{
    memset(buff_C, 0, sizeof(buff_C));

    const arm_cfft_instance_f32 *instance(0);

    if (flag)
    { // init instance
        switch (FFT_point)
        {
        case 16:
            instance = &arm_cfft_sR_f32_len16;
            break;
        case 32:
            instance = &arm_cfft_sR_f32_len32;
            break;
        case 64:
            instance = &arm_cfft_sR_f32_len64;
            break;
        case 128:
            instance = &arm_cfft_sR_f32_len128;
            break;
        case 256:
            instance = &arm_cfft_sR_f32_len256;
            break;
        case 512:
            instance = &arm_cfft_sR_f32_len512;
            break;
        case 1024:
            instance = &arm_cfft_sR_f32_len1024;
            break;
        case 2048:
            instance = &arm_cfft_sR_f32_len2048;
            break;
        case 4096:
            instance = &arm_cfft_sR_f32_len4096;
            break;
        default:
            flag = false;
            break;
        }

        if (!flag)
        {
            printf("length error\n");
        }
    }

    if (flag)
    { // load wave data

        bool loading = true;

        while (loading)
        {
            static char str_buff[100];
            scanf("%99[^\n]%*[^\n]", str_buff);
            getchar();

            uint16_t idx = 0;
            float32_t R = 0;
            float32_t I = 0;

            if (!strncmp(str_buff, "abort", 5))
            {
                flag = false;
                loading = false;
            }
            else if (!strncmp(str_buff, "end", 3))
            {
                loading = false;
            }
            else if (3 == sscanf(str_buff, "%hu %f %f", &idx, &R, &I))
            {
                if (idx < FFT_point)
                {
                    buff_C[idx * 2 + 0] = R;
                    buff_C[idx * 2 + 1] = I;
                }
            }
            else
            {
                // NOP
            }
        }

        if (!flag)
        {
            printf("wave load error\n");
        }
    }

    if (flag)
    { // execute FFT

        HAL_TIM_GenerateEvent(&htim2, TIM_EVENTSOURCE_UPDATE);
        HAL_TIM_Base_Start(&htim2);

        arm_cfft_f32(instance, buff_C, 0, 1);

        HAL_TIM_Base_Stop(&htim2);
    }

    if (flag)
    { // dump result

        printf("CFFT f32 %hu processing time %.6f sec\n", FFT_point, htim2.Instance->CNT * 1e-6f);

        for (int16_t i = -FFT_point / 2; i < FFT_point / 2; i++)
        {
            int16_t idx = i >= 0 ? i : i + FFT_point;

            printf("%d %f %f\n",
                    i,
                    buff_C[idx * 2 + 0],
                    buff_C[idx * 2 + 1]);
        }
    }
}

if (1 == sscanf(str, "RFFT %hu", &FFT_point))
{
    memset(buff_C, 0, sizeof(buff_C));

    arm_rfft_fast_instance_f32 instance = {};

    if (flag)
    { // init instance
        flag = flag && (ARM_MATH_SUCCESS == arm_rfft_fast_init_f32(&instance, FFT_point));

        if (!flag)
        {
            printf("instance init error (invalid length?)\n");
        }
    }

    float32_t *const buff_R = &buff_C[4096]; // real

    if (flag)
    { // load wave data

        bool loading = true;

        while (loading)
        {
            static char str_buff[100];
            scanf("%99[^\n]%*[^\n]", str_buff);
            getchar();

            uint16_t idx = 0;
            float32_t R = 0;

            if (!strncmp(str_buff, "abort", 5))
            {
                flag = false;
                loading = false;
            }
            else if (!strncmp(str_buff, "end", 3))
            {
                loading = false;
            }
            else if (2 == sscanf(str_buff, "%hu %f", &idx, &R))
            {
                if (idx < FFT_point)
                {
                    buff_R[idx] = R;
                }
            }
            else
            {
                // NOP
            }
        }

        if (!flag)
        {
            printf("wave load error\n");
        }
    }

    if (flag)
    { // execute FFT

        HAL_TIM_GenerateEvent(&htim2, TIM_EVENTSOURCE_UPDATE);
        HAL_TIM_Base_Start(&htim2);

        arm_rfft_fast_f32(&instance, buff_R, buff_C, 0);

        HAL_TIM_Base_Stop(&htim2);
    }

    if (flag)
    { // dump result

        printf("RFFT f32 %hu processing time %.6f sec\n", FFT_point, htim2.Instance->CNT * 1e-6f);

        for (int16_t i = 0; i < FFT_point / 2; i++)
        {
            int16_t idx = i;

            printf("%d %f %f\n",
                    i,
                    buff_C[idx * 2 + 0],
                    buff_C[idx * 2 + 1]);
        }
    }
}

結果

　複素数(CFFT)の場合は負の周波数も扱うことができます。実部のみ(RFFT)の場合は負の周波数は扱えません。
　以下に出てくるグラフの縦軸はCFFT/RFFTの値そのままです。横軸はグラフ化の際に補正しています。

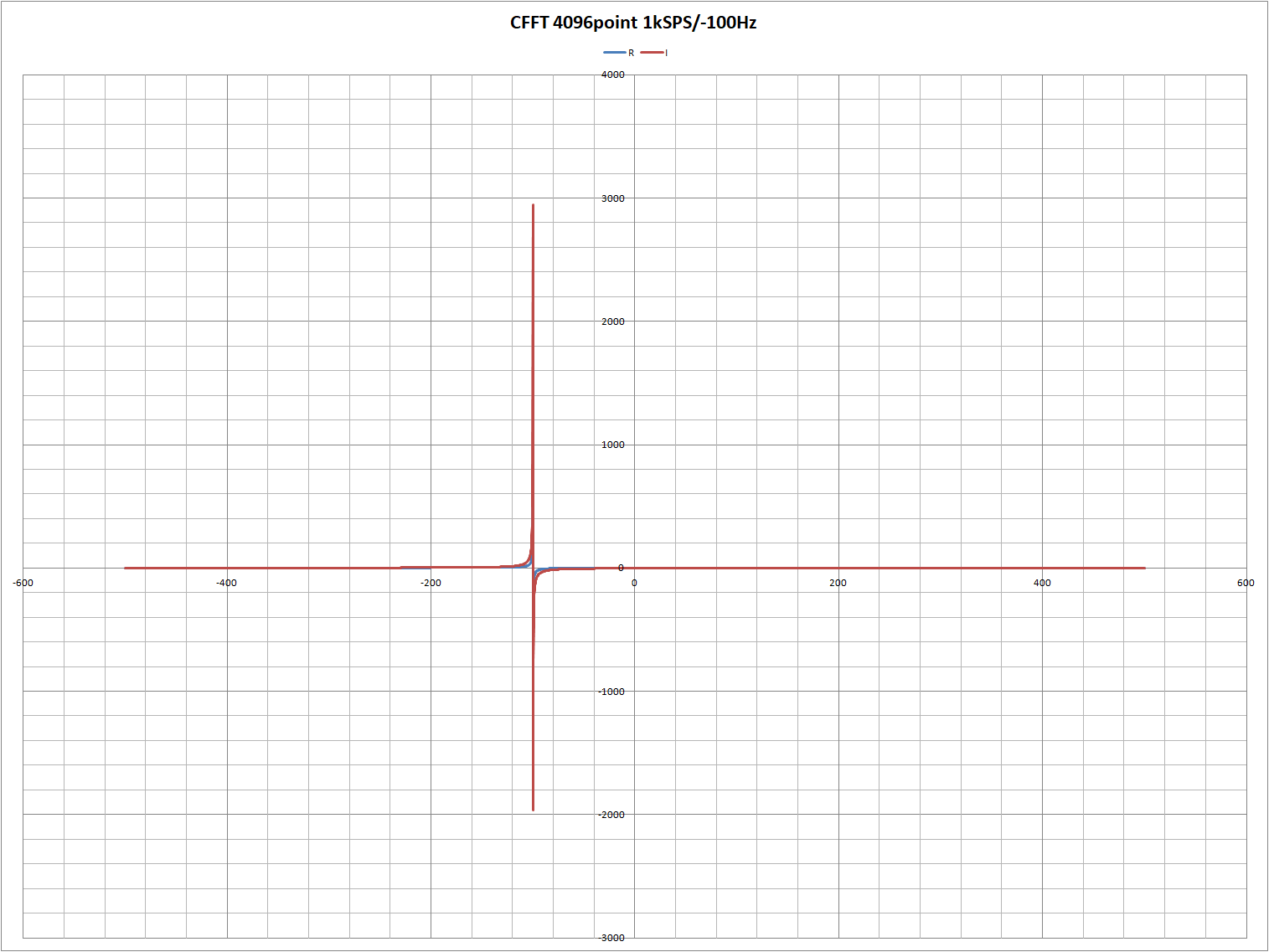
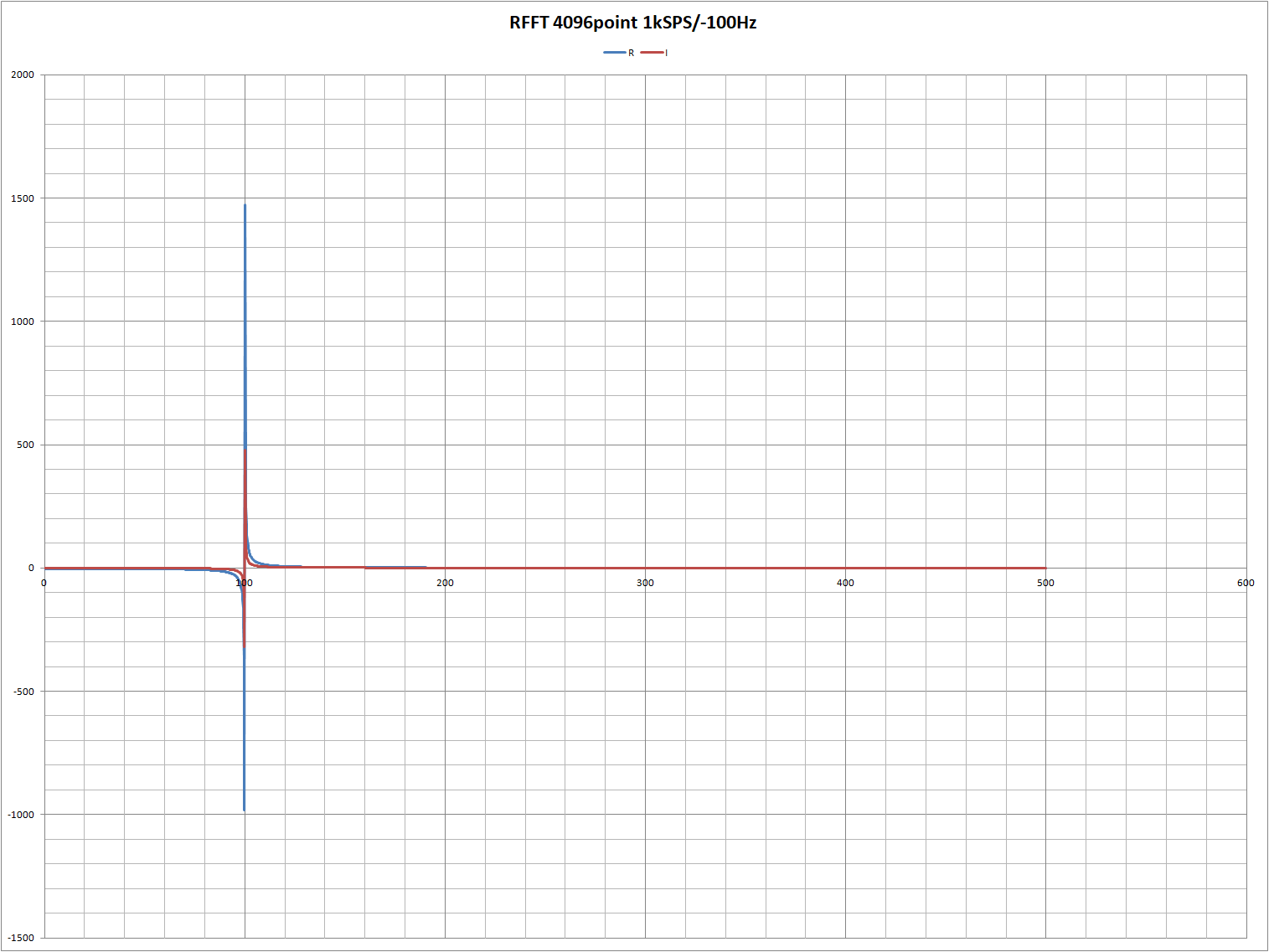
　試しに1kSPS/-100Hzの4096ポイントの波形を与えてみます。

2018-06-29_9-59.png

2018-06-29_10-01.png

　CFFTは正しく負の周波数も扱えています。RFFTは負の周波数を与えても正の周波数として処理してしまいます。
　RFFTの結果は0Hzを軸に対象となるので、負の周波数領域は出力されません。

　結果の実部/虚部にスペクトルが出ているのは、周波数がFFT的にちょうどいい周波数ではないためです。例えば1024SPS/100Hzなら綺麗なスペクトルが見られます。

　RFFTは入力バッファと出力バッファが別ですが、入力バッファも破壊的なので、破壊されると困る場合は別の領域にコピーした上で処理してください。
　CFFTは言わずもがな、入力バッファを上書きして出力します。

　値の入力例は以下のようになります。
　1024SPS/-128Hz 32ポイント

CFFT 32     
0   1.000   0.000 
1   0.707   -0.707 
2   0.000   -1.000 
3   -0.707  -0.707 
4   -1.000  0.000 
5   -0.707  0.707 
6   0.000   1.000 
7   0.707   0.707 
8   1.000   0.000 
9   0.707   -0.707 
10  0.000   -1.000 
11  -0.707  -0.707 
12  -1.000  0.000 
13  -0.707  0.707 
14  0.000   1.000 
15  0.707   0.707 
16  1.000   0.000 
17  0.707   -0.707 
18  0.000   -1.000 
19  -0.707  -0.707 
20  -1.000  0.000 
21  -0.707  0.707 
22  0.000   1.000 
23  0.707   0.707 
24  1.000   0.000 
25  0.707   -0.707 
26  0.000   -1.000 
27  -0.707  -0.707 
28  -1.000  0.000 
29  -0.707  0.707 
30  0.000   1.000 
31  0.707   0.707 
end

　結果は以下のようになります。

CFFT f32 32 processing time 0.000015 sec
-16 0.000000 0.000000
-15 0.000000 0.000000
-14 0.000000 0.000000
-13 0.000000 0.000000
-12 0.000000 0.000000
-11 0.000000 0.000000
-10 0.000000 0.000000
-9 0.000000 0.000000
-8 0.000000 0.000000
-7 0.000000 0.000000
-6 0.000000 0.000000
-5 0.000000 0.000000
-4 31.997585 0.000000
-3 0.000000 0.000000
-2 0.000000 0.000000
-1 0.000000 0.000000
0 0.000000 0.000000
1 0.000000 0.000000
2 0.000000 0.000000
3 0.000000 0.000000
4 0.000000 0.000000
5 0.000000 0.000000
6 0.000000 0.000000
7 0.000000 0.000000
8 0.000000 0.000000
9 0.000000 0.000000
10 0.000000 0.000000
11 0.000000 0.000000
12 0.002416 0.000000
13 0.000000 0.000000
14 0.000000 0.000000
15 0.000000 0.000000

　FFT result indexから周波数にするにはindex / FFTポイント数 * サンプリングレートで計算できます。この場合、1024Hzで32ポイントなので、-4は-4 / 32 * 1024 = -128となり、正しく-128Hzにピークが出ています。

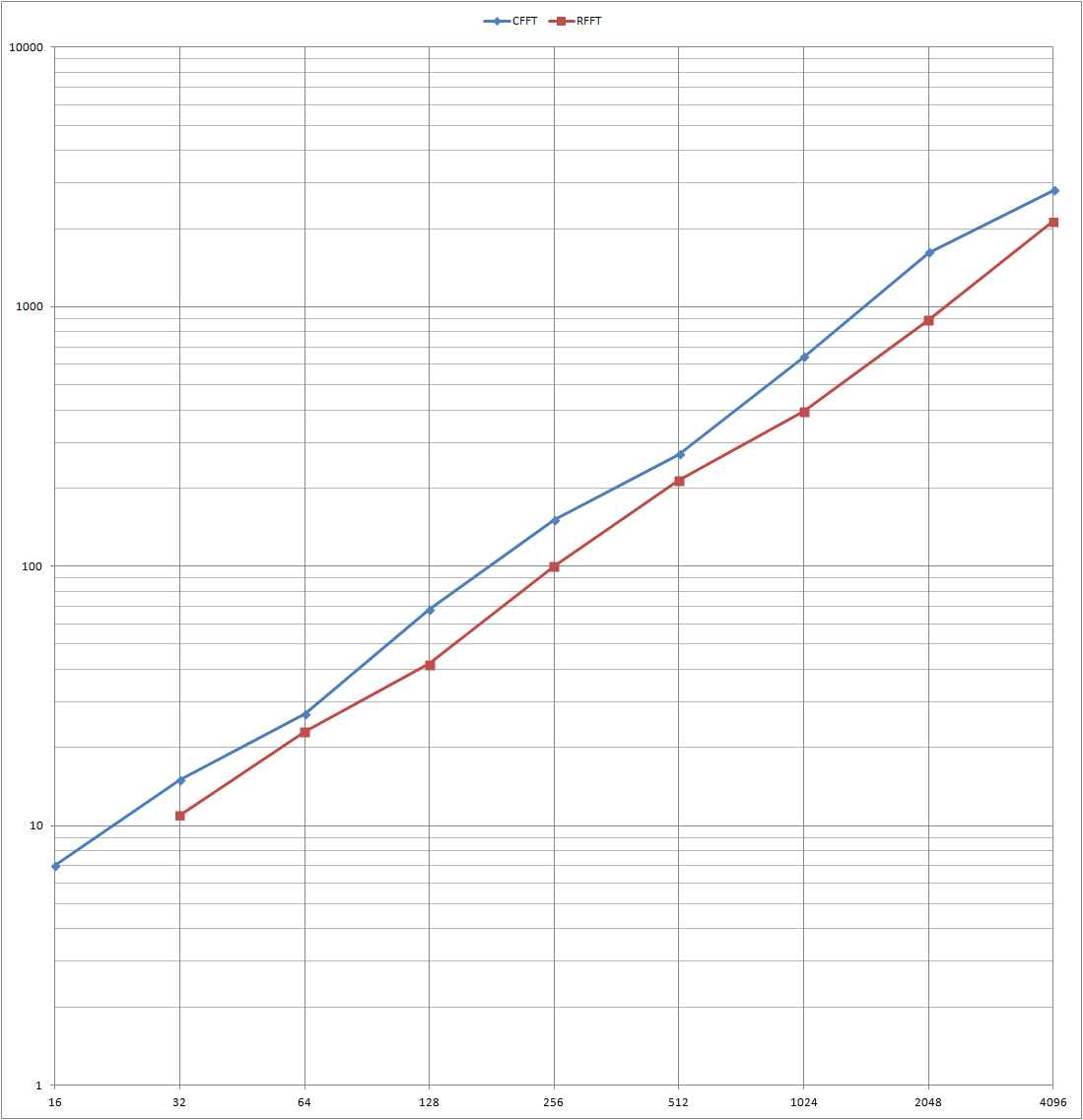
　FFT計算時間は以下のとおりです。

points CFFT RFFT
16 7usec -
32 15usec 11usec
64 27usec 23usec
128 68usec 42usec
256 151usec 100usec
512 270usec 214usec
1024 641usec 396usec
2048 1620usec 894usec
4096 2805usec 2130usec

image.png

　ほぼポイント数に比例して計算時間も伸びています。

3
4
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
3
4