人工衛星の軌道をざっくり計算する #C#

ライブラリ

　en.wikipediaの外部リンクからダウンロードする

Simplified perturbations models - Wikipedia

　en.wikipedia.org/wiki/SGP4にアクセスすればリダイレクトされるので、検索エンジンが使えない環境でどうしてもSGP4のソースコードが今すぐ必要、みたいなときはここを使うと便利(そんな状況あるのか?)。

　C++, FORTRAN, Pascal, and MATLABからZIPファイルをダウンロードし、その中のsgp4/cs/SGP4Lib/SGP4Lib/SGP4Lib.csを使用する。

　なお、今回は.NET Framework 4.7.2環境で動作確認を行った。使用するライブラリはかなり古いので、もっと前のバージョンでも動くはず。あとのバージョン(.NET 7とか)でも動くはず。C言語実装をC#に移植した感じなので、C#らしく使いたいとか、自分で手を加えようとするとちょっと面倒かも。ガッツリ使いたい場合は別のライブラリを使ったほうが良さそう。

修正

　デフォルトではSystem.Windows.Formsに依存するコードが含まれているので、コンソール環境等の場合は削除する。
　public class InputBoxを削除し、これを呼び出している部分も適当に処理する(実装を削除+例外を投げるとか)。
　それと、メソッドgstimeを使いたいので、privateをpublicへ変更しておく。
　あとは不要なusingを削除したりとか。

使用方法

　最初にusing SGP4Methods;を宣言しておく。

　基本的にはSGP4Libのインスタンスを経由して処理を行うので、まずvar sgp4 = new SGP4Lib();のようにインスタンスを確保しておく。

TLEの読み込み

　続いて、TLEを読み込む。今回は41896U 16080A ARASE(ERG)の軌道を使用した(後々の動作確認の際に、適当な離心率があったほうがわかりやすいため)。

sgp4.twoline2rv(
    "1 41896U 16080A   20001.67702290 +.00000307 +00000-0 +29667-3 0  9992",
    "2 41896 031.3057 216.9740 7041743 060.4973 351.2527 02.53786126028097",
    ' ', ' ', ' ',
    SGP4Lib.gravconsttype.wgs84,
    out _, out _, out _, out var satrec);

　ASCIIコードで指定するオプションはとりあえず空白を指定しておいた。それと、地球楕円体はWGS84を指定した。本来はWGS72を使うべきらしいのだが、ざっくりとした位置を知りたいだけならWGS84でも問題なさそう。

ケプアリアン→カルテシアン

　SGP4Lib.sgp4で指定した時間の位置と速度が求まる。時間は元期からの経過時間[分]を指定する。とりあえず経過時間0を指定し、TLEの元期でのカルテシアン6要素を求める。

var r = new double[3];
var v = new double[3];
sgp4.sgp4(ref satrec, 0, r, v);
Console.WriteLine(string.Join(", ", r));
Console.WriteLine(string.Join(", ", v));
Console.WriteLine(sgp4.mag(r) + " " + sgp4.mag(v));

-6769.71370635225, -5099.75020713959, -0.00685694873666178
6.98747569515968, -3.25085705053331, 4.13582300510747
8475.6401434488 8.74630894052031

　位置のZがほぼゼロで速度のZが正なので、昇交点から数ミリ秒の場所に元期があるとわかる。

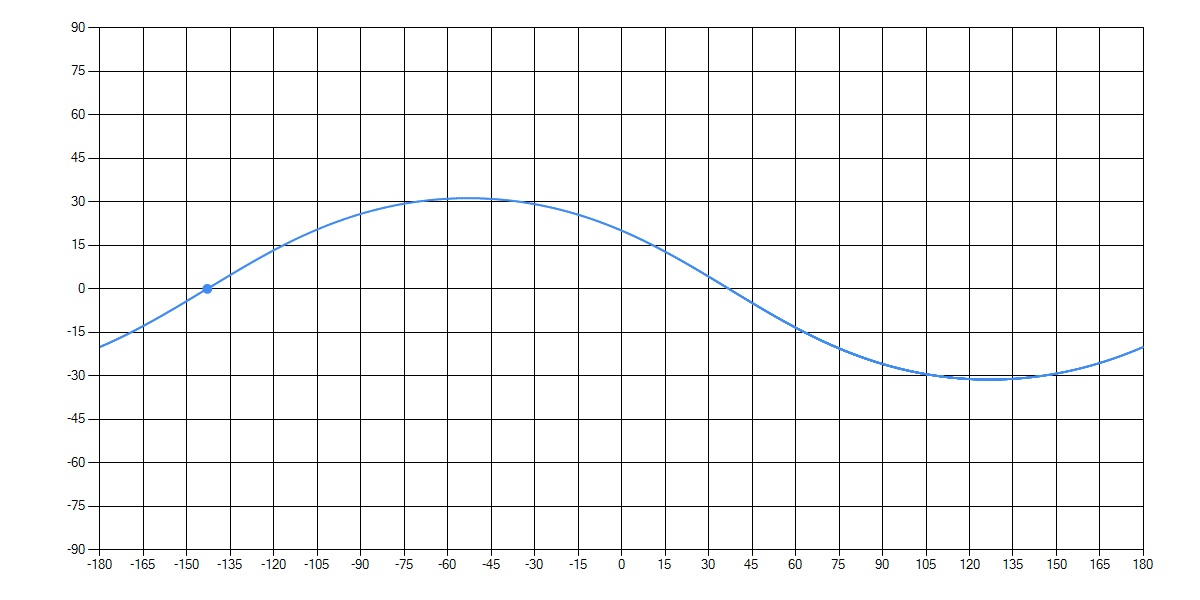
　適当な範囲(とりあえず1周回分)を極座標へ変換してグラフ化すると、以下のようになる。

　丸点が元期での位置を示している。
　sgp4で出力される座標は慣性空間で表現されたものであり、地図上に表示するためには座標変換が必要となる。

　地球の姿勢はグリニッジ恒星時で表現され、SGP4Lib.gstimeで求めることができる。例えばsgp4の引数に時間[分]を変数minで与える場合、satrecの元期にこれを加算してgstimeに与えると求めた位置・速度の時点での地球の姿勢が得られるから、これを使用して座標変換を行う。

var rad = -sgp4.gstime(satrec.jdsatepoch + satrec.jdsatepochF + min / 1440);
var cos = Math.Cos(rad);
var sin = Math.Sin(rad);

(r[0], r[1]) = (
    r[0] * cos - r[1] * sin,
    r[0] * sin + r[1] * cos);
(v[0], v[1]) = (
    v[0] * cos - v[1] * sin,
    v[0] * sin + v[1] * cos);

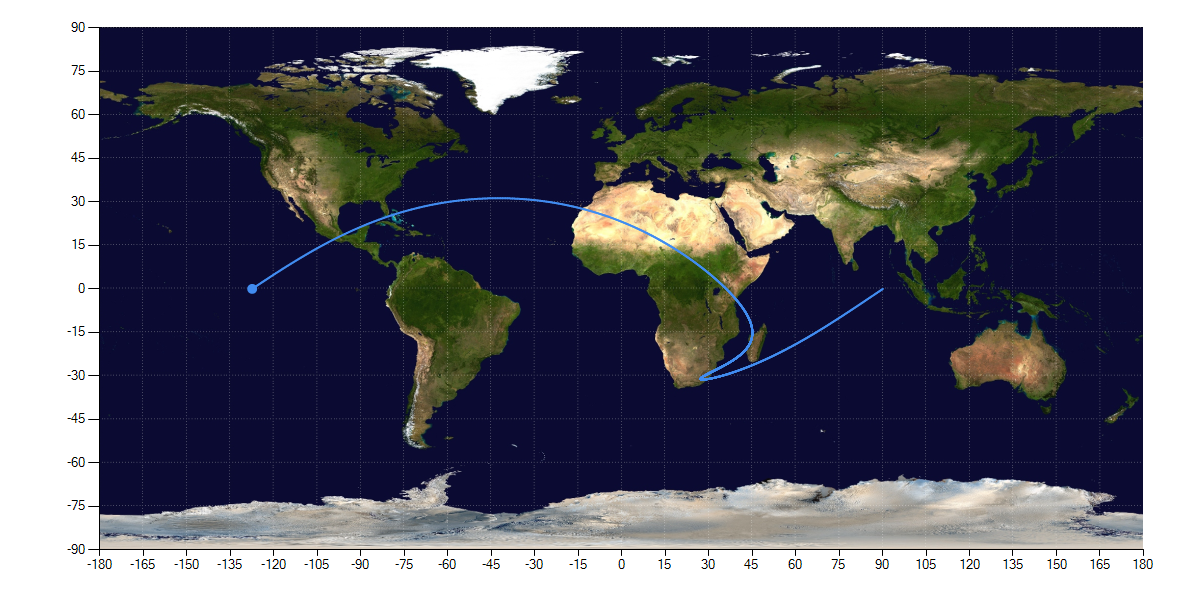
　この座標変換を行った上で極座標をグラフ化すると以下のようになる。

　他の軌道表示ソフトで表示される地図上の軌道と同じような形が表示される。

　なお、今回は雑にatan2(y, x), atan2(z, sqrt(x * x + y * y))のような形で座標変換を行っている。今回の例では緯度方向で0.2度程度の誤差が発生するが、1) このグラフの解像度ではほとんど識別できない 2) 真面目に計算すると実装が凄く面倒、というような理由によって球による近似を使用した。
　背景画像にはWikimedia経由で公開されているパブリックドメインの画像を使用した(File:Equirectangular-projection.jpg - Wikimedia Commons)

時刻を指定して位置を計算

var date = DateTimeOffset.Parse("2020-01-02T03:04:05.06+09:00").UtcDateTime;
sgp4.jday(date.Year, date.Month, date.Day,
    date.Hour, date.Minute, date.Second + date.Millisecond / 1e3, out var jd, out var jdF);
var min = ((jd - satrec.jdsatepoch) + (jdF - satrec.jdsatepochF)) * 1440;

var r = new double[3];
var v = new double[3];
sgp4.sgp4(ref satrec, min, r, v);

{
    var rad = -sgp4.gstime(jd + jdF);
    var cos = Math.Cos(rad);
    var sin = Math.Sin(rad);

    (r[0], r[1]) = (
        r[0] * cos - r[1] * sin,
        r[0] * sin + r[1] * cos);
    (v[0], v[1]) = (
        v[0] * cos - v[1] * sin,
        v[0] * sin + v[1] * cos);
}

Console.WriteLine(string.Join(", ", r));
Console.WriteLine(string.Join(", ", v));
Console.WriteLine(sgp4.mag(r) + " " + sgp4.mag(v));

17923.0909105361, 17504.6592312723, -5019.72833648759
0.0216240678136964, 3.23773149080859, -1.77754333925778
25550.8895180275 3.69364767267022

　SGP4Lib.jdayでjdを求め、satrecのjdとの差で経過時間を求める。

カルテシアン→ケプラリアン

　位置と速度のベクトルからケプラリアンを求めることができる。
　あまり使うことはないが、直交座標空間で質点の位置・速度を伝播させて遊んだりしているとこういう機能が欲しくなる。

var r = new double[3];
var v = new double[3];
sgp4.sgp4(ref satrec, 0, r, v);

sgp4.getgravconst(SGP4Lib.gravconsttype.wgs84,
    out _, out var mu, out var radiusearthkm,
    out _, out _, out _, out _, out _);
sgp4.rv2coe(r, v, mu,
    out _, out var a, out var ecc, out var incl, out var omega,
    out var argp, out var nu, out var m, out _, out _, out _);

Console.WriteLine(a);
Console.WriteLine(ecc);
Console.WriteLine(incl / Math.PI * 180);
Console.WriteLine(omega / Math.PI * 180);
Console.WriteLine(argp / Math.PI * 180);
Console.WriteLine(nu / Math.PI * 180);
Console.WriteLine(m / Math.PI * 180);

var revPerDay = Math.Sqrt(mu / Math.Pow(a, 3) / (4 * Math.Pow(Math.PI, 2))) * 86400;
Console.WriteLine(revPerDay);

Console.WriteLine(a - a * ecc - radiusearthkm);
Console.WriteLine(a + a * ecc - radiusearthkm);

　軌道長半径と離心率以外はラジアンで与えられるので、度に換算して表示する(TLEでは度で与えられるから、見比べたときに便利なため)。

22699.3578017824
0.704966321311411
31.3050710306861
216.991465245519
60.4955438237343
299.504366965702
351.236710754657
2.53853080476841
318.938036128379
32323.5035674364

　上から

軌道長半径
離心率
軌道傾斜角
昇交点赤経
近地点引数
真近点角
平均近点角
平均運動
近地点
遠地点

　が表示される。
　平均運動は出力されないので、軌道長半径から求める。近地点・遠地点は簡単な計算で求まるので、ついでに表示している。TLEに含まれる数字はある程度の精度で得られている。

　この際、離心率が小さい衛星の値を与えるとTLEの数値と大きく乖離した数値が出力される(仮に軌道が真円の場合、近点角を基準にした数字が拘束できない)。ケプラリアンへの変換の確認を行う際は注意すること。

その他

SGP4Lib.getgravconstで地球楕円体のパラメータを得られるが、ここには離心率の値が入っていない。J2項から扁平率fが得られる。

var f = 1.5 * (j2 + (Math.Pow(radiuskm, 3) * Math.Pow(7.292115e-5, 2)) / (3 * mu));

　ここで7.292115e-5は地球の角速度(rad/s)。ただし計算では定数に対してあまり精度のいい値は得られない。

　例えばgetgravconstでWGS84を指定した場合、GM=398600.5、RE=6378.137、J2=0.00108262998905が得られ、上記の計算によって離心率1/298.094519、短半径6356.740642が得られる(実際の値は1/298.257223563、6356.7523142)。地球の大きさに対して半径で12m程度は誤差みたいなものだが、最近では単独測位でもその程度の精度が得られるので、実際のアプリケーションでは無視できない量になる。