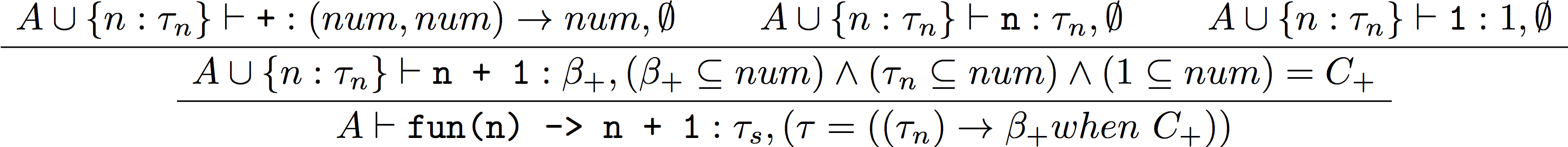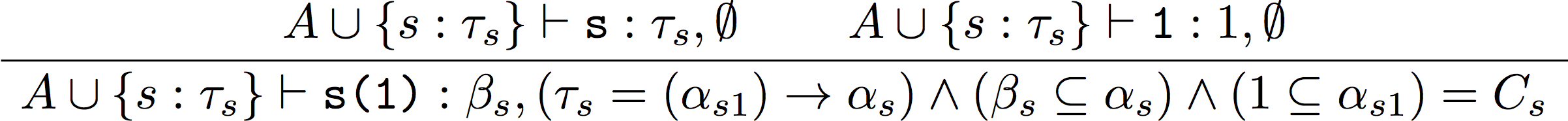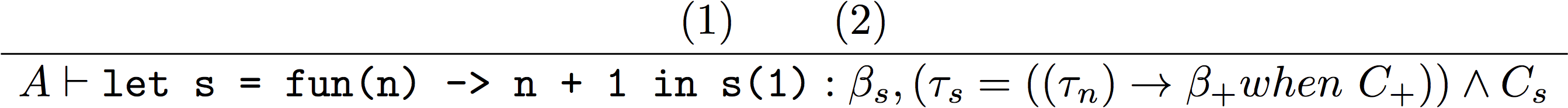Dialyzer の型推論アルゴリズムについて

この記事は 第2のドワンゴ Advent Calendar 22日目の記事として書かれました。

ドワンゴ新卒の @amutake です。仕事では Erlang を書いています。
今回は Erlang の静的型検査ツールである Dialyzer が採用している 成功型付け (success typings) という型付けの手法について調べたので簡単に紹介します。

(本当は Coq で回転寿司屋の店内を形式化して設計した回転寿司システムがお客さんを満足させることを証明した話が書きたかったのですが、証明が終わりませんでした)

Dialyzer の不満点

Erlang を書いている人はほぼ全員使っているであろう静的型検査ツールの Dialyzer ですが、いくつか不満点があります。

• メモリを食いまくる
• 時間がかかる
• ときどきよくわからない推論をする

メモリを食いまくることと時間がかかることについてはこの記事では触れず、推論部分に焦点を当てていきます。
(ちなみに Dialyzer は Erlang で実装されているのですが、実装言語を Erlang ではなく別の言語に変えるだけでメモリの問題と時間がかかる問題はだいぶよくなる気がします…。Erlang はこの手のツールの実装には向いていない気がします)

Dialyzer の推論

普通の (と言ってしまいます) 静的型付き言語に慣れていると、Dialyzer の型検査結果は少し変に思うことがあります。
いくつか例を挙げていきます。
(spec は型宣言、when はガード、変数は大文字始まり、アトム (シンボル) は小文字始まり、だけわかっていればなんとなく読めると思います)

-module(dialyzer_test).
-compile(export_all).

%% ============
%% 引数について
%% ============

%% 引数の型がまったく異なる場合
%% これはエラー (当たり前)
%% Invalid type specification for function dialyzer_test:f0/1. The success typing is (atom()) -> 0
-spec f0(integer()) -> integer().
f0(A) when is_atom(A) -> 0.

%% 引数の型が、型宣言のほうが小さい場合
%% エラーは起きない (変っちゃ変だが安全) が、
-spec f1(integer()) -> integer().
f1(A) when is_atom(A) -> 0;
f1(N) when is_integer(N) -> N.

-spec g1() -> any().
g1() -> f1(a). % ここでエラーになる (まあ当たり前) The call dialyzer_test:f1('a') breaks the contract (integer()) -> integer()

%% 引数の型が、型宣言のほうが大きい場合
%% エラーは起きない (なぜ？) が、
-spec f2(atom() | integer()) -> integer().
f2(N) when is_integer(N) -> N.

-spec g2() -> any().
g2() -> f2(a). % ここでエラーになる (関数宣言は通ったのに？) The call dialyzer_test:f2('a') will never return since it differs in the 1st argument from the success typing arguments: (integer())


%% ==============
%% 返り値について
%% ==============

%% 返り値の型がまったく異なる場合
%% これはエラー (当たり前)
%% Invalid type specification for function dialyzer_test:f3/1. The success typing is (integer()) -> integer()
-spec f3(integer()) -> atom().
f3(N) when is_integer(N) -> N.

%% 返り値の型が、型宣言のほうが大きい場合
%% エラーは起きない
-spec f4(integer()) -> atom() | integer().
f4(N) when is_integer(N) -> N.

%% これもエラーは起きない
-spec g4_1() -> integer().
g4_1() -> f4(0).

%% これはエラー
%% Invalid type specification for function dialyzer_test:g4_2/0. The success typing is () -> integer()
-spec g4_2() -> atom().
g4_2() -> f4(0).

%% 返り値の型が、型宣言の方が小さい場合
%% エラーは起きない
-spec f5(atom() | integer()) -> integer().
f5(A) when is_atom(A) -> A;
f5(N) when is_integer(N) -> N.

%% これもエラーは起きない
-spec g5_1() -> integer().
g5_1() -> f5(a).

%% これはエラー
%% Invalid type specification for function dialyzer_test:g5_2/0. The success typing is () -> integer()
-spec g5_2() -> atom().
g5_2() -> f5(a).

若干直感的ではないものがあると思うのですが、どういうアルゴリズムでこういう結果になるんでしょうか。

Dialyzer の推論アルゴリズムは、すごいE本 によると、「成功型付け」という手法がもとになっているらしいので調べてみます。

成功型付けのアルゴリズムを追う

ということで、成功型付けの論文を読んでいきます。
論文は Practical Type Inference Based on Success Typings (pdf) です。

以下の特徴があるようです。

• サブタイピングベース
• 実行時にはエラーがでない 嘘でしたすみません。健全性は満たしていません。
• 型宣言が書かれていなくても動作する

型推論は以下の2段階から成ります。

1. コードを解析して、導出ルールに沿って制約を生成する (constraint generation)
2. 制約を満たす解を見つける (constraint solving)

constraint generation

コードを解析して 制約 (constraint) を生成するフェーズです。導出ルールは論文の Figure 2 にあります。制約とは、型変数に対する条件です。

(この論文のなかでは、Erlang のサブセットである mini-erlang という言語が使われています)

型環境 $A$ (普通は $\Gamma$ だと思うのですが、論文にあわせて $A$ にします)、式 $e$、型 $\tau$、制約 $C$ を使って、型判断を $A \vdash e : \tau, C$ と書きます (型環境が $A$ だったとき、$C$ という制約のもとで式 $e$ は型 $\tau$ を持つ)。

この導出ルールを使って、制約 C を作っていきます。

では、例として let s = fun(n) -> n + 1 in s(1) という式について考えます。この程度でも導出木は大きくなるので、3つに分けます。なお、一行が小さくなるので、 number() 型は num と書きます。

型付け規則はちょうど構文木のルール毎になっているので、構文木について分解していき、それぞれの型付け規則を当てはめます。型変数は適当なものを導入していけばOKです。
そうやっていくと、以下のようになります。

↑(1)

↑(2)

↑全体

全体の制約は、$(\tau_s = ((\tau_n) \rightarrow\beta_+ when \ ((\beta_+ \subseteq num) \wedge (\tau_n \subseteq num) \wedge (1 \subseteq num)))) \wedge (\tau_s = (\alpha_{s1}) \rightarrow \alpha_s) \wedge (\beta_s \subseteq\alpha_s) \wedge (1 \subseteq \alpha_{s1})$ となります。

constraint solving

次に得られた制約から、型変数から具体型を得る 解 (solution) という関数を計算します。
$Sol \models C$ と書いて、$Sol$ が制約 $C$ の解になっているという意味になります。

解は以下のように帰納的に導出できます。

($Sol_1 \sqcup Sol_2$ は $Sol_1$ と $Sol_2$ の上限を取る操作)

この操作によって導かれた型シグネチャ $(\alpha_1, \alpha_2, \dots, \alpha_n) \rightarrow \beta$ に対して、
関数呼び出しの各パラメータ $p_i$ と返り値 $v$ に対して $p_1 \in \alpha_1 \wedge p_2 \in \alpha_2 \wedge \dots \wedge p_n \in \alpha_n \wedge v \in \beta$ を満たせば、安全な関数呼び出しになっている、ということになります。

じゃあどうするかですが、まずすべての型変数を any() 型としてやります。そこから制約を満たすように型を小さくしていく (any はすべての値の集合なので、そこから小さくしていく)、という流れになります。

let s = fun(n) -> n + 1 in s(1) の例だと、まずは以下のように得られた制約に現れる型変数すべてを any とします。

Sol = { τ_s: any, τ_n: any, β_+: any, β_s: any, α_s1: any, α_s: any }

制約を満たすように型を小さくしていくと

Sol = { τ_s: (num) -> num, τ_n: num, β_+: num, β_s: num, α_s1: num, α_s: num }

となります。これで、全体の型は number() とわかりました。

spec はどこに

推論アルゴリズムを見てわかるように、spec については全く出てきません。
実はこの論文が書かれたときは spec は使われていなかったようです。この論文のあとから Dialyzer が spec も見るようになったとのことです。
論文中でも、型宣言がなくても動くようにする、と書いていたりするので、spec はあくまでも補助的なもので、spec が明らかに間違っていなければまあOKという感じなのだと思います (要出典)。

では最初の例について spec なしで考えると、明らかに間違っている関数はエラーになり、問題なさそうな関数は通るので、この例については問題はありません。

ただ、以下のコードは integer() を受け取る関数に number() 型の値を渡しているのでエラーになって欲しいのにも関わらず、通ります。これは成功型付けの欠点です。

% -spec f(integer()) -> 'ok'.
f(N) when is_integer(N) -> ok.

% -spec g(number()) -> number().
g(N) when is_number(N) -> N + 1.

h() -> f(g(1.1)). % これが通る。実行時にエラーになる。

なぜこれが起こるかですが、App 規則をよく見てみるとわかります。自分で型推論してみてください。
(最後の宣伝の本では詳しく解説しています。)

まとめ

以上のような型推論アルゴリズムになっていることがわかりました。

spec に書かれた型シグネチャをどのように扱っているのかはまだきちんと調べられていないですが、 spec はドキュメントとしての意味もあるので、あまり適当に扱われると厳しいです。
また、この論文が書かれた当時はわかりませんが、どちらにしろ spec は必ず書くようにしている人/チームが多いと思うので、もっと spec の情報を使えばより正確な型検査ができるようになるのではないかなと思ったりしました。

宣伝

というような話をより詳しく・かつ発展的な内容も書いたものを 技術書典2 に出しますので、よろしくお願いします！ サークル名 進捗大陸 う-17