はじめに
データ分析では結果を二値(0,1)で出力するようなタスクが扱われることが多くあります。
ここでは、その結果を分析する時に使える基本的な評価指標を紹介します。
混同行列(confusion matrix)
これから紹介する評価指標を理解する上で押さえておく必要があるのが混同行列(confusion matrix)というものです。
これは各サンプルを「実際の分類」と「予測結果による分類」により4つに分けたものになっていて、以下のような行列です。
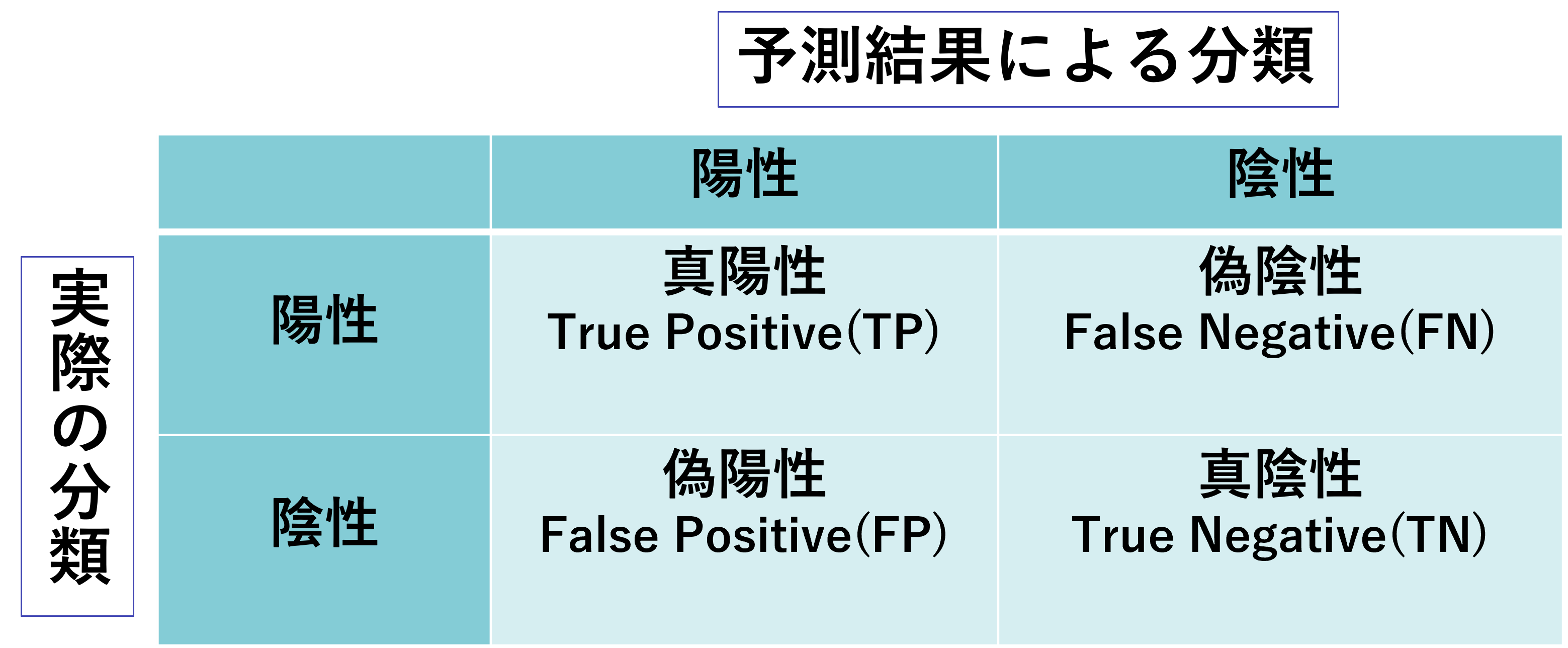
二値分類のタスクが用いられる例としては、病気の有無や作物の病害の有無、機械の傷の有無などの診断が考えられ、このようなタスクでは主に「異常を検出すること」が目的となります。ここでは、「異常がある」=「陽性」= 1、「異常がない」= 「陰性」= 0として機械の傷を検知するタスクを行うことを考えます。
すると混同行列の各要素は以下のように解釈できます。
| 要素名 | 説明 |
|---|---|
| 真陽性(TP) | 「傷があると予測」して「実際に傷がある」(正解) |
| 偽陰性(FN) | 「傷がないと予測」して「実際は傷がある」(不正解) |
| 偽陽性(FP) | 「傷があると予測」して「実際は傷がない」(不正解) |
| 真陰性 (TN) | 「傷がないと予測」して「実際に傷がない」(正解) |
このように単に予測が正解、不正解かだけでなく、「陽性と陰性のどちらを予測したうえでその結果になったか」を考えることでより詳細な評価が可能になります。
正確性(accuracy)
全ての予測の内、正解の割合を表したシンプルな指標です。
混同行列の値で表すと、正確性 a は以下の計算で求められます。
a = \frac{TP+TN}{TP+TN+FP+FN}
わかりやすい指標ではありますが、この指標があまり有用とならない場合があります。
それは予測が片方のラベルに偏っている場合です。これは解析するデータでラベルがどちらかに偏るときによく起こります。
例として、手元に1000サンプルのデータがあり、そのうち900個が陰性、100個が陽性であるデータを用いて機械学習モデルに学習させた結果、すべて陰性と判断した場合を考えてみましょう。
すると900サンプルについて正確な予測ができているので正確性 a は以下のように計算されます。
a = \frac{900}{1000} = 0.9
陽性のサンプルを全く予測できていないのにも関わらず、良さそうなスコアが出てしまいました。
これでは正しく評価できているとは言えません。実際の解析でも陽性のデータが少ない場合は多くあり、病気の診断などでも陽性を正しく予測することが重要となることを考えると、もっと有用な指標を考える必要があります。
正確性は単純でわかりやすいが参考にならない指標であると言えます。
適合率(Precision)
陽性と予測したサンプルの内、実際に陽性だったサンプルの割合です。
混同行列の値で表すと、適合率 p は以下の計算で求められます。
p = \frac{TP}{TP+FP}
先程と同様に、1000サンプルのデータがあり、そのうち900個が陰性、100個が陽性であるデータを用いて機械学習モデルに学習させた結果、すべて陰性と判断した場合を考えてみましょう。
p = \frac{0}{0+0} = 0
なんと0になってしまいました。陽性を一切予測できていないという結果が反映されていますね。
極端な例であったため、次の例として、1000サンプルのデータがあり、そのうち900個が陰性、100個が陽性であるデータを用いて機械学習モデルに学習させた結果、100個のデータを陽性と判断し、そのうち50個が実際に陽性、50個は陰性であった場合を考えてみましょう。
p = \frac{50}{50+50} = 0.5
この指標にも、有用とならない場合が考えられます。それは陽性サンプルの分布と、予測が陽性に偏る場合です。
ここでは最初の例とは反対に、1000サンプルのデータがあり、そのうち900個が陽性、100個が陰性であるデータを機械学習モデルに学習させた結果、すべて陽性と判断した場合を考えてみましょう。
p = \frac{900}{900+100} = 0.9
今度は陰性を一切予測できていないのに、良さそうなスコアが出てしまいました。
この指標は陰性と予測されたデータの数を一切考慮せず、陽性と予測されたデータを全体として、その中の正しい予測の割合を表しています。そのため陰性の予測精度については軽視されてしまうことに注意が必要です。
また、900個が陽性、100個が陰性で1サンプルのみを陽性と判断し、実際にそれが陽性だった場合についても考えると
p = \frac{1}{0+1} = 1.0
となり、残り899個の予測を誤っているのに高いスコアが出てしまいます。
これらのことから適合率は陽性を間違いなく予測できるかを判断するには適した指標であると言えます。
再現率(Recall)
実際に陽性であるサンプルの内、陽性と予測されたサンプルの割合です。
混同行列の値で表すと、正確性 a は以下の計算で求められます。
r = \frac{TP}{TP+FN}
まずこれまで用いた例で、再現性 r を求めてみましょう。
例1 : 1000サンプルのデータがあり、そのうち900個が陰性、100個が陽性であるデータを用いて機械学習モデルに学習させた結果、すべて陰性と判断した場合
r = \frac{0}{0+100} = 0
例2 : 1000サンプルのデータがあり、そのうち900個が陰性、100個が陽性であるデータを用いて機械学習モデルに学習させた結果、100個のデータを陽性と判断し、そのうち50個が実際に陽性、50個は陰性であった場合
r = \frac{50}{50+50} = 0.5
例3 : 1000サンプルのデータがあり、そのうち900個が陽性、100個が陰性であるデータを機械学習モデルに学習させた結果、すべて陽性と判断した場合
r = \frac{900}{900+0} = 1.0
**例4 :900個が陽性、100個が陰性で1サンプルのみを陽性と判断し、実際にそれが陽性だった場合
r = \frac{1}{1+899} ≒ 0.001
例1、例2では適合率と同様の値ですが、例3、例4で異なる値を取っています。例4に関しては適合率より直感的な値となっていますが、例3に関しては完全な予測ではないのに1.0という値を取ってしまっており直感に反します。極端な例を考えてみましょう。
**例5:1000サンプル中10個が陽性、990個が陰性で全てを陽性と予測した場合
r = \frac{10}{10+0} ≒ 1.0
予測が陽性に偏っている場合は再現率は高くなってしまうことがわかりました。
これらのことから適合率は陽性を取りこぼしなく予測できるかを判断するには適した指標であると言えます。
F1-score
適合率と再現率の調和平均をとったものなります。
混同行列の値で表すと、F1-score F は以下の計算で求められます。
F = \frac{2TP}{2TP+FP+FN}
調和平均とは2つの値の逆数の和で個数を割った値であり、導出過程は以下のようになっています。
F = \frac{2}{1/P+1/R} = \frac{2}{(TP+FP)/TP+(TP+FN)/TP} = \frac{2TP}{2TP+FP+FN}
この指標は定義からもわかるように適合率と再現率の両方を反映させているため、双方の弱点を補うことができている指標となっています。例を見ていきましょう。
例1 : 1000サンプルのデータがあり、そのうち900個が陰性、100個が陽性であるデータを用いて機械学習モデルに学習させた結果、すべて陰性と判断した場合
F = \frac{0}{0+0+100} = 0
例2 : 1000サンプルのデータがあり、そのうち900個が陰性、100個が陽性であるデータを用いて機械学習モデルに学習させた結果、100個のデータを陽性と判断し、そのうち50個が実際に陽性、50個は陰性であった場合
F = \frac{100}{100+50+50} = 0.5
例3 : 1000サンプルのデータがあり、そのうち900個が陽性、100個が陰性であるデータを機械学習モデルに学習させた結果、すべて陽性と判断した場合
r = \frac{1800}{1800+100+0} = 0.9
**例4 :900個が陽性、100個が陰性で1サンプルのみを陽性と判断し、実際にそれが陽性だった場合
r = \frac{2}{2+0+899} ≒ 0.001
**例5:1000サンプル中10個が陽性、990個が陰性である時、全てを陽性と予測した場合
r = \frac{20}{20+990+0} ≒ 0.02
陰性の予測ができていない例3以外は小さな値を取るようになりました。両方の弱点を補い合うことができていますね。
ただ、陰性の予測にも注目したい場合は適さないのは、適合率と再現率と同様です。
これらのことからF1_scoreは適合率と再現率をバランスよく評価する指標であると言えます。
まとめ
今回は代表的な二値分類の尺度について解説しました。ここで紹介したものの他に、同様に混同行列を用いて算出する値として「Matthews係数」や「G-mean」、陽性と陰性を決定する閾値を変化させて算出するROC系の評価指標などもあるため、自分で評価指標を考える際は、十分に調べた上でデータ分析・モデル作成の目的に沿った評価指標の設定してみてください。時間ができたら、これらの評価指標についてもまとめたいと思います!お疲れ様です。