完全独習 統計学入門

読書記録

読者プロフィール

組込み系エンジニア。
統計学は大学の授業で受けたような受けなかったような。忘れてしまった。

仕事ではセンサの性能評価でデータをとったり平均や標準偏差を求めることはあった。ただセンサの性能測定だとスペック表に答えが書かれているので統計って感じではない。統計・・・エンジニアを名乗るなら知っておいたほうが良いんだろうなぁ。でも全然知らないなぁ。

雑感

表紙の「使うのは中学数学だけ！」に偽りはない。数学記号としては不等式とルートくらいしか登場しない。データ数を常に有限（5個くらい）として例示してくれるのでΣも出てこない。

確率について、どうやら著者は確率の専門家のようだが本書では確率については「コインの裏が出る確率は1/2」「サイコロの各目は1/6」くらいしか出てこない。筆者曰く統計学で推測を使うには確率理論が必要らしいのですが、本書ではばっさり切っているとのこと。細かいことは素人には分からないが、統計学を道具として使う上での理解・イメージを得たい私としてはとても助かる。

ほとんど数学を使わず最終的に 「[未知のデータ（母集団）]の集まりから、いくつかデータを取り出して、そのデータを分析することで［未知のデータ］の特徴を推測する」 について納得感を得られるように説明されている。統計学の他の本は読んだことがないが、恐らくかなり分かり易くイメージを掴める良書なのだと思う。

あらすじ

かなり丁寧に（ゆっくりと少しずつ）説明してくれているため21章という多めな章立てになっているが、その実は以下の２つで、これらをとにかく丁寧に噛み砕き積み上げている構成となっている。
①標準偏差と推定
②測定可能なサンプル（標本集団）から、無限である母集団の母平均と母標準偏差を推定する（本書のゴール）

私自身の記録のために「丁寧な記載」はカットしてキーワードや要点のみ記載するが、実際はものすごく丁寧に書かれているので誤解なきよう。

95%予言的中区間

この言葉は本書では頻繁に出てくるが、著者オリジナルの造語。本書は無限の母集団について特徴量を推定していくのだが、ざっくりいうと95%予言(推定)が当たる区間。可能な母数の入るべき区間とのこと。区間推定と呼ぶ。

標準偏差

正規分布するデータにおけるばらつきの度合いを示す値を標準偏差と呼ぶ。
標本数n、各データXn、標本平均X-(エックスバー)において
標準偏差は以下となる。

標準偏差=\sqrt{\frac{Σ(x_n-\bar{x})^2}{n}}

※簡単のためにΣを記載しているが本書では出てこない。

標準正規分布

分布表で各値は求まるもの。
平均値は0となり、標準偏差は1となる。以下のような分布のこと。

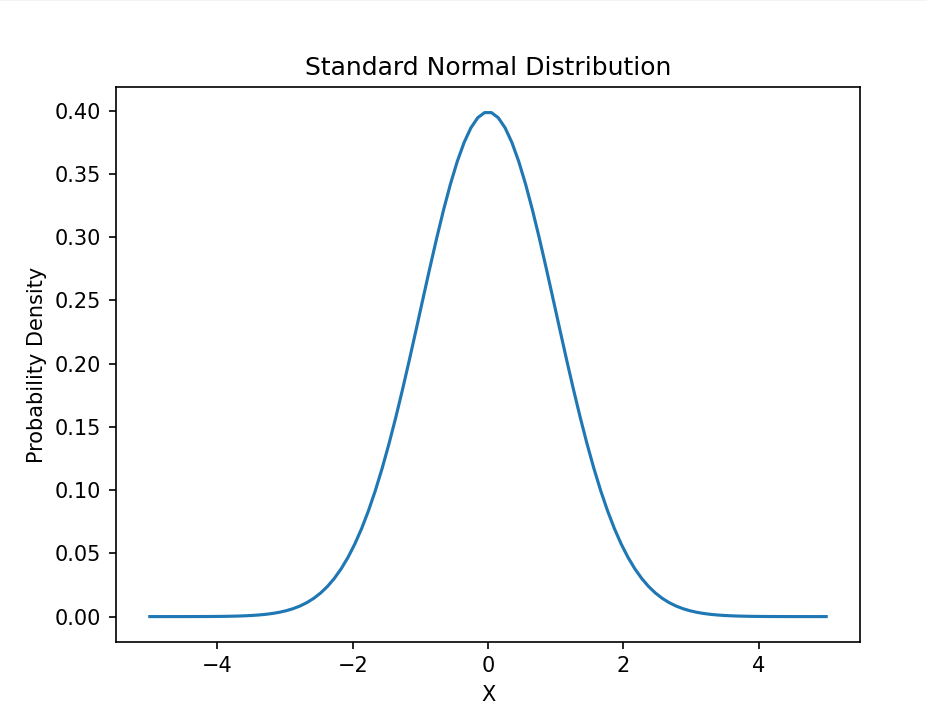
一般正規分布

世の中にみられる様々な正規分布のかたち。標準正規分布を以下のように計算したもの

一般正規分布データ＝σ×標準正規分布データ＋μ

平均値をμ、
標準偏差をσとしたとき、95%予言的中区間は以下のようになる

-1.96 ≦ \frac{x-μ}{σ} ≦ 1.96

母集団からサンプリングした標本集団の特徴

母平均をμ
母標準偏差をσにおいて

標本数nの標本平均X-(エックスバー)は正規分布であり
X-の平均値はμ
X-の標準偏差は以下のように縮む

\frac{σ}{\sqrt{n}}

X-の95%予言的中区間

-1.96 ≦ \frac{x-μ}{\frac{σ}{\sqrt{n}}} ≦ 1.96

母平均と母標準偏差の推定

本書のゴールはこの２つの推定。それぞれ推定にあたりカイ二乗分布とt分布について知る必要がある。これらの概要は本書に記載されている。いずれの分布も分布表があり数値を決定できるため、統計量がカイ二乗分布かt分布か分かれば数値で推定できる。

カイ二乗分布を用いた母分散の推定

標本数をn、標本分散をs2(2乗)する。これらは何れもデータから算出できる。
求めたい母分散σ2(2乗)とする。これは現時点ではわからない。
統計量Wを以下とする。このWはカイ二乗分布する。

W=\frac{s^2n}{σ^2} 

カイ二乗分布の各自由度(n)の分布表は値が決まっているため、95%予言的中区間の定数をピックアップすることでWの範囲は数値で示すことができ、結果的に母分散s2の区間を推定できる。

カイ二乗分布の自由度1~5は以下のようになる。

t分布を用いた母平均の推定

標本数をn、標本平均X-(エックスバー)、標本標準偏差sとする。これらは何れもデータから算出できる。
求めたい母平均をμとする。これは現時点ではわからない。
統計量Tを以下とする。このTはt分布する。

T=\frac{(\bar{x}-μ)\sqrt{n-1}}{s} 

カイ二乗分布同様にt分布の各自由度(n)の分布表は値が決まっているため、95%予言的中区間の定数をピックアップすることでTの範囲は数値で示すことができ、結果的に母平均μの区間を推定できる。

ｔ分布の自由度1~5は以下のようになる。