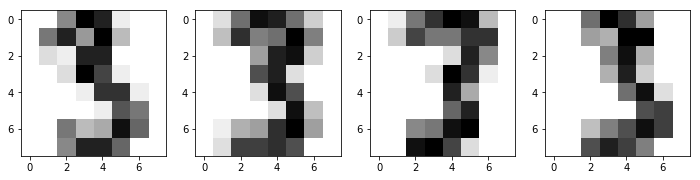この記事では、PRMLの第12章で述べられている、確率的主成分分析をPythonで実装します。
対応するjupyter notebookは筆者のgithubリポジトリにあります。連載全体の方針や、PRMLの他のアルゴリズムの実装については、連載のまとめページをご覧いただければと思います。
9, 10章と同様に、今回も教師なし学習のお話です。導出は、ガウス分布の一般公式をそのまま応用するだけなので、今回も数式は軽めです。最尤法とベイズ的アプローチ、両方を実装して比較を行います。
1 理論のおさらい
1.1 設定
- $N \in \mathbb{N}$ : 観測データ点の個数
- $d \in \mathbb{N}$ : 各観測データ点の次元
- $x_0, x_1, \dots , x_{N-1} \in \mathbb{R}^d$ : 観測データ点
- データ点をまとめて行列$X$で表します。ただし、$X_{n,i}$は$x_n$の第$i$成分とします。
主成分分析では、$d$次元のデータをより低い次元の点を用いて表現することにより、「圧縮」を行います。
1.2 モデル
- $m \in \mathbb{N}$ : 潜在空間の次元
- $z_0, \dots, z_{N-1} \in \mathbb{R}^{m}$ : 観測データ点に対応する潜在変数
- 潜在変数をまとめて行列$Z$と表します。ただし、$Z_{n,i}$は$z_n$の第$i$成分とします。
潜在変数に対して、実際に観測できる変数$x_n$を観測変数と呼ぶことにします。
1.2.1 最尤法
最尤法による確率的主成分分析では、以下のモデルを用います。
$$
\begin{align}
&{} p\left(X,Z \middle| W, \mu, \sigma^2 \right) = \prod_{n=0}^{N-1} p\left(x_n \middle| z_n, W, \mu, \sigma^2 \right)p(z_n) \
&{} p\left(z \right) := \mathcal{N}\left(z \middle| 0, I_m \right) \
&{} p\left(x \middle|z, W, \mu, \sigma^2 \right) := \mathcal{N}\left(x \middle| W z + \mu, \sigma^2 I_d \right),
\end{align}
$$
ただし、
- $\mathcal{N}\left(\cdot \middle| \mu , \Sigma \right)$は平均$\mu$、共分散行列$\Sigma$のガウス分布の確率密度を表します。
- $\mu \in \mathbb{R}^d$であり, $W$は$d \times m$行列、$\sigma > 0$です。これらがモデルのパラメーターです。
1.2.2 ベイズ的アプローチ
ベイズ的アプローチ1では、$W$に事前分布を仮定し、次のモデルを用います。
$$
\begin{align}
&{} p\left(X, Z, W \middle| \alpha, \mu, \sigma^2 \right) := p\left(X,Z \middle| W, \mu, \sigma^2 \right) p(W| \alpha) \
&{} p\left(W \middle| \alpha \right) = \prod_{i=0}^{m-1} \left[ \left( \frac{\alpha_i}{2\pi}\right)^{d/2} \exp\left( - \frac{1}{2} \alpha_i w_{i}^{T} w_i \right) \right]
\end{align}
$$
ただし、
- $p\left(X,Z \middle| W, \mu, \sigma^2 \right)$は先ほどのモデルと同一です。
- $W = (w_0, w_1, \dots, w_{M-1})$と表し、$w_{i} \in \mathbb{R}^d$は列ベクトルとします。
1.3 推論
1.3.1 最尤法(解析解)
最尤法では、下記の尤度関数(具体形はPRML(12.43)参照)を最大化するパラメーター$\mu, W, \sigma^2$を求めます:
$$
\begin{align}
p\left(X \middle| \mu, W, \sigma^2 \right) := \int p\left(X,Z \middle| \mu, W, \sigma^2 \right) dZ,
\end{align}
$$
この最大化問題に対する解析解は以下で与えられます2:
$$
\begin{align}
\mu &= \bar{x} := \frac{1}{N} \sum_{n=0}^{N-1} x_n \
W &= U_m \left(L_m - \sigma^2 I \right)^{1/2} \
\sigma^2 &= \frac{1}{d-m} \sum_{i=m}^{d-1} \lambda_i,
\end{align}
$$
ただし、
- $U_m$は$d \times m$行列で、その各列はデータ共分散行列$S$(定義はすぐ下で与えます)の固有ベクトルであり、対応する固有値が最も大きい$m$個を選んできます。
- $\lambda_i$は$S$の固有値を表します。
- $L_m$は$m \times m$対角行列で、その対角要素は$U_m$の列である固有ベクトルに対応する固有値$\lambda_i$です。
なお、$S$は次で定義されます:
$$
\begin{align}
S := \frac{1}{N} \sum_{n=0}^{N-1} (x_n - \bar{x}) (x_n - \bar{x})^T,
\end{align}
$$
1.3.2 最尤法(EMアルゴリズム)
先ほど述べたように、最尤法を用いる場合は解析解を得ることができますが、代わりにEMアルゴリズムを用いて反復的に解を得ることもできます。
こちらのアプローチの利点についてはPRMLの12.2.2にもありますが、簡潔に述べると:解析解を得るためには$S$の固有値分解を行う必要があり、この計算に$\mathcal{O}(d^3)$かかります。従って、$d$が大きいときはEMアルゴリズムを用いると計算を高速化できるかもしれません3。
まず、$\mu$についての最大化は容易に行えます:
$$
\begin{align}
\mu = \bar{x} := \frac{1}{N} \sum_{n=0}^{N-1}x_n.
\end{align}
$$
この節では以下、$\mu$はこの値に固定します。
確率的主成分分析に対するEMアルゴリズムでは、パラメーター$W$と$\sigma^2$を次のように更新していきます。
$$
\begin{align}
& W_{new} = \left[ \sum_{n=0}^{N-1} (x_n - \bar{x}) \mathbb{E}_{old}[z_n]^T \right]
\left[ \sum_{n=0}^{N-1} \mathbb{E}_{old}[z_n z_{n}^{T}] \right]^{-1} \
& \sigma^{2}_{new} = \frac{1}{ND}\sum_{n=0}^{N-1}
\left[ | x_n - \bar{x} |^2 - 2 \mathbb{E}_{old}\left[ z_n\right]^T W_{new}^{T} (x_n-\bar{x})
{} + \mathrm{Tr}\left( \mathbb{E}_{old}\left[ z_n z_{n}^{T} \right] W_{new}^{T} W_{new} \right) \right] \
& \mathbb{E}_{old}\left[ z_n \right] := M_{old}^{-1} W_{old}^{T} \left( x_n - \bar{x} \right) \
& \mathbb{E}_{old}\left[ z_n z_{n}^{T} \right] := \sigma_{old}^{2} M_{old}^{-1} +
\mathbb{E}_{old}\left[ z_n \right] \mathbb{E}_{old}\left[ z_n \right]^T \
& M_{old} := W_{old}^{T} W_{old} + \sigma_{old}^{2} I_m
\end{align}
$$
1.3.3 ベイズ的アプローチ
ベイズ的アプローチでは、以下の周辺尤度関数を最大化する$\mu, \alpha, \sigma^2$を求めます:
$$
\begin{align}
p\left(X \middle| \alpha, \mu, \sigma^2 \right) &:= \int p\left(X,Z \middle| W, \mu, \sigma^2 \right) p\left(W \middle| \alpha \right) dW dZ \
&= \int p\left(X \middle| W, \mu, \sigma^2 \right) p\left(W \middle| \alpha \right) dW
\end{align}
$$
再び、$\mu$についての最大化は容易に行えます:
$$
\begin{align}
\mu = \bar{x} := \frac{1}{N} \sum_{n=0}^{N-1}x_n.
\end{align}
$$
この節では、$\mu$の値はこの値で与えられるとします。
さて、この積分は解析的に解くことができません。そこで、近似を行うことにします。ここでは$W$についての積分にLaplace近似を用います。Hessianに由来する係数を無視する4ことにより、周辺尤度の最大化は、以下の関数を最大化する$W, \sigma^2, \alpha$を求めることに帰着されます:
$$
\begin{align}
& \frac{d}{2} \sum_{i=0}^{m-1} \log \alpha_i + \log p\left( X \middle| W, \mu, \sigma^2 \right)
{} - \frac{1}{2} \sum_{i=0}^{m-1} \alpha_i | w_i |^2
\end{align}
$$
この最大化を、反復法を用いて行います。具体的には、以下のようにパラメーターの更新を行います5:
$$
\begin{align}
& W_{new} = \left[ \sum_{n=0}^{N-1} (x_n - \bar{x}) \mathbb{E}_{old}[z_n]^T \right]
\left[ \sum_{n=0}^{N-1} \mathbb{E}_{old}[z_n z_{n}^{T}] + \sigma_{old}^{2} A \right]^{-1} \
& A = \mathrm{diag}\left( \alpha_{i, old} \right) \
& \sigma^{2}_{new} = \frac{1}{ND}\sum_{n=0}^{N-1}
\left[ | x_n - \bar{x} |^2 - 2 \mathbb{E}_{old}\left[ z_n\right]^T W_{new}^{T} (x_n-\bar{x})
{} + \mathrm{Tr}\left( \mathbb{E}_{old}\left[ z_n z_{n}^{T} \right] W_{new}^{T} W_{new} \right) \right] \
& \mathbb{E}_{old}\left[ z_n \right] := M_{old}^{-1} W_{old}^{T} \left( x_n - \bar{x} \right) \
& \mathbb{E}_{old}\left[ z_n z_{n}^{T} \right] := \sigma_{old}^{2} M_{old}^{-1} +
\mathbb{E}_{old}\left[ z_n \right] \mathbb{E}_{old}\left[ z_n \right]^T \
& M_{old} := W_{old}^{T} W_{old} + \sigma_{old}^{2} I_m \
& \alpha_{i,new} = \frac{d}{\|w_{i,new}\|^2}
\end{align}
$$
1.4 変換と逆変換
新しい観測データ点を$\xi$、対応する潜在変数を$\zeta$と表します。
学習が終わったモデルを用いて次の操作を行うことができます:
- 観測変数$\xi$が与えられたときに、これを潜在変数$\zeta$に変換する。
- 潜在変数$\zeta$が与えられたときに、これを観測変数$\xi$に逆変換する。
前者は観測データを圧縮するために用いられるかと思います。
後者は圧縮したデータを元に戻すためにも用いることができますし、また、観測データのサンプルを生成するために用いることもできます。
この記事では確率モデルを考えているので、変換/逆変換の出力も確率分布となります:
$$
\begin{align}
&{} p\left( \zeta \middle| \xi, X, W, \mu, \sigma^2 \right) = \mathcal{N}\left( \zeta \middle| M^{-1} W^T (\xi - \mu), \sigma^2 M^{-1} \right) \
&{} p\left( \xi \middle| z, W, \mu, \sigma^2 \right) = \mathcal{N}\left( \xi \middle| W\zeta + \mu, \sigma^2 I_d \right) ,
\end{align}
$$
ただし、$M:= W^T W + \sigma^2 I_m$です6。
なお、ベイズ的アプローチの場合は正確には$W$について積分する必要がありますが、この積分は解析的には実行できません。そこで、$W$についての事後分布を単純に(Laplace近似で得られた$W$にピークを持つ)デルタ関数で置き換えました。この(だいぶ粗い)近似の下では、上記の変換/逆変換の式は、ベイズ的アプローチについても成り立ちます。
2 数式からコードへ
では、ここまで数式で書いてきたものをコードに変換していきましょう。
この記事では最尤推定による主成分分析を行うMLPCAクラスと、ベイズ推論による主成分分析を行うBPCAクラスを実装します。
まず2.1節でMLPCAクラスを実装し、これを継承して2.2節でBPCAクラスを実装します。
2.1 MLPCAクラス
2.1.1 概要:データ属性とメソッド
データ属性
-
m: $m$, i.e., 潜在空間の次元 -
d: $d$, i.e., 観測変数の次元 -
W: $W$, (d, m) numpy array -
mu: $\mu$, (d, ) numpy array -
variance: $\sigma^2$
メソッド
-
_fit_analytical: 解析解を求めて学習を行うメソッド。 -
_init_params: EMアルゴリズムのためにパラメーターW,varianceを初期化するメソッド。初期化の仕方は入力X(観測変数)に依存するとする。 -
_estep: EMアルゴリズムのE-stepを行うメソッド。具体的には、$\mathbb{E}_{old}\left[ z_n \right]$と$\sum_{n=0}^{N-1} \mathbb{E}_{old}\left[ z_n z_{n}^{T} \right]$を計算して返す。 -
_mstep: EMアルゴリズムのM-stepを行うメソッド。具体的には、$W$を$\sigma^2$更新する。$\mathbb{E}_{old}\left[ z_n \right]$と$\sum_{n=0}^{N-1} \mathbb{E}_{old}\left[ z_n z_{n}^{T} \right]$を入力として受け付ける。 -
_fit_em: EMアルゴリズムを用いて学習を行うメソッド。 -
fit: 学習を行うメソッド。method引数の値によって、解析解かEMアルゴリズムかを選択できるようにしておく。 -
transform: 観測変数のデータを入力として受け取り、潜在変数に変換する。 -
inverse_transform: 潜在変数を入力として受け取り、観測変数に変換する。
2.1.2 解析解 _fit_analytical
_fit_analyticalでは、解析的にパラメーターを求めます。
繰り返しになりますが、解析解では、パラメーターを次のように定めます:
$$
\begin{align}
\mu &= \bar{x} := \frac{1}{N} \sum_{n=0}^{N-1} x_n \
W &= U_m \left(L_m - \sigma^2 I \right)^{1/2} \
\sigma^2 &= \frac{1}{d-m} \sum_{i=m}^{d-1} \lambda_i,
\end{align}
$$
- $U_m$は$d \times m$行列。その各列はデータ共分散行列$S$の固有ベクトルで、対応する固有値が最も大きい$m$個
- $\lambda_i$は$S$の固有値
- $L_m$は$m \times m$対角行列で、その対角要素は$U_m$の列である固有ベクトルに対応する固有値$\lambda_i$
ただし、
$$
\begin{align}
S := \frac{1}{N} \sum_{n=0}^{N-1} (x_n - \bar{x}) (x_n - \bar{x})^T,
\end{align}
$$
これをコードに翻訳するのはstraightforwardですね。対応するコードは次のようになります。
なお、$S$を求める際にnp.covを利用しますが、上の式の通りのものを出すためには、ddof=0にしておく必要があります。
def _fit_analytical(self, X):
self.d = len(X[0])
self.mu = np.mean(X, axis=0)
S = np.cov(X, rowvar=False, ddof=0)
eigenvals, eigenvecs = eigh(S)
ind = np.argsort(eigenvals)[::-1][0:self.m] # sort the eigenvalues in decreasing order, and choose the largest m
eigenvals_largest = eigenvals[ind]
eigenvecs_largest = eigenvecs[:, ind]
if self.d != self.m:
self.variance = 1/(self.d - self.m) * np.sum(np.sort(eigenvals)[::-1][self.m:])
else:
self.variance = 0.0
self.W = eigenvecs_largest @ np.diag( np.sqrt(eigenvals_largest - self.variance) )
2.1.3 パラメーター初期化 _init_params
解析解は片付いたので、次にEMアルゴリズムを考えていきます。まずはパラメーターの初期化です。
外から初期値を指定できるようにしておきましょう。デフォルト値としては、データの典型的なスケールはだいたい1だろうという仮定を暗において、適当に初期値を与えます(コード部分参照)。
また、
- 観測変数の空間の次元
dは、ここで入力Xに応じて決めることにします。 -
muはXの平均として固定されるので、ここで求めておきます。
def _init_params(self, X, W=None, variance=None):
'''
Method for initializing model parameterse based on the size and variance of the input data array.
Parameters
----------
X : 2D numpy array
2D numpy array representing input data, where X[n, i] represents the i-th element of n-th point in X.
W : 2D numpy array, default None
2D numpy array representing the initial value of parameter W
variance : positive float, default is None
positive float representing the initial value of parameter variance
'''
self.d = len(X[0])
self.mu = np.mean(X, axis=0)
self.W = np.eye(self.d)[:,:self.m] if (W is None) else W # probably there are better initializations
self.variance = 1.0 if (variance is None) else variance
2.1.4 _estep
準備が整ったら、いよいよEMアルゴリズムの本体を走らせるためのメソッドを実装していきます。
E-stepでは、次の2つの期待値を求めます。
$$
\begin{align}
& \mathbb{E}_{old}\left[ z_n \right] := M_{old}^{-1} W_{old}^{T} \left( x_n - \bar{x} \right) \
& \mathbb{E}_{old}\left[ z_n z_{n}^{T} \right] := \sigma_{old}^{2} M_{old}^{-1} +
\mathbb{E}_{old}\left[ z_n \right] \mathbb{E}_{old}\left[ z_n \right]^T \
& M_{old} := W_{old}^{T} W_{old} + \sigma_{old}^{2} I_m
\end{align}
$$
ただし、$\mathbb{E}_{old}\left[ z_n z_{n}^{T} \right]$は次のM-stepでは$\sum_{n=0}^{N-1} \mathbb{E}_{old}\left[ z_n z_{n}^{T} \right]$の形でしか効いてこないので、$n$について和をとった後のものを返すことにします。
def _estep(self, X):
'''
Method for performing E-step, returning
$\mathbb{E}_{old}\left[ z_n \right]$ and $\sum_{n=0}^{N-1} \mathbb{E}_{old}\left[ z_n z_{n}^{T} \right]$
Parameters
----------
X : 2D numpy array
2D numpy array representing input data, where X[n, i] represents the i-th element of n-th point in X.
Returns
----------
Ez : 2D numpy array
(len(X), self.m) array, where Ez[n, i] = $\mathbb{E}_{old}[z_n]_i$
sumEzz : 2D numpy array
(self.m, self.m) array, where sumEzz[i,j] = $\sum_{n=0}^{N-1} \mathbb{E}_{old}\left[z_n z_{n}^{T} \right]_{i,j}$
'''
Minv = np.linalg.inv( (self.W).T @ self.W + self.variance*np.eye(self.m) ) # we only use inverse of the matrix M
dX = X - self.mu
Ez = dX @ self.W @ (Minv.T)
sumEzz = len(X) * self.variance * Minv + (Ez.T) @ Ez
return Ez, sumEzz
2.1.5 _mstep
次に、$W$と$\sigma^2$を更新します。
$$
\begin{align}
& W_{new} = \left[ \sum_{n=0}^{N-1} (x_n - \bar{x}) \mathbb{E}_{old}[z_n]^T \right]
\left[ \sum_{n=0}^{N-1} \mathbb{E}_{old}[z_n z_{n}^{T}] \right]^{-1} \
& \sigma^{2}_{new} = \frac{1}{ND}\sum_{n=0}^{N-1}
\left[ | x_n - \bar{x} |^2 - 2 \mathbb{E}_{old}\left[ z_n\right]^T W_{new}^{T} (x_n-\bar{x})
{} + \mathrm{Tr}\left( \mathbb{E}_{old}\left[ z_n z_{n}^{T} \right] W_{new}^{T} W_{new} \right) \right]
\end{align}
$$
def _mstep(self, X, Ez, sumEzz):
'''
Method for performing M-step, and updating model parameters
Parameters
----------
X : 2D numpy array
2D numpy array representing input data, where X[n, i] represents the i-th element of n-th point in X.
Ez : 2D numpy array
(len(X), self.m) array, where Ez[n, i] = $\mathbb{E}_{old}[z_n]_i$
sumEzz : 2D numpy array
(self.m, self.m) array, where sumEzz[i,j] = $\sum_{n=0}^{N-1} \mathbb{E}_{old}\left[z_n z_{n}^{T} \right]_{i,j}$
'''
dX = X - self.mu
self.W = ((dX.T) @ Ez) @ np.linalg.inv(sumEzz)
self.variance = ( np.linalg.norm(dX)**2 - 2*np.trace(Ez @ (self.W.T) @ (dX.T) ) + np.trace( sumEzz @ self.W.T @ self.W ) ) /(len(X)*self.d)
2.1.6 _fit_em
ここまでの_init_params, _estep, _mstepをまとめてEMアルゴリズムを走らせるメソッドを実装しておきます。
収束判定は、$W$と$\sigma^2$の変化が十分小さいか否かで行うことにします。
def _fit_em(self, X, max_iter=100, tol=1e-4, disp_message=False, W0=None, variance0=None):
'''
Method for performing fitting by EM algorithm
Parameters
----------
X : 2D numpy array
2D numpy array representing input data, where X[n, i] represents the i-th element of n-th point in X.
max_iter : positive int
The maximum number of iteration allowed
tol : positive float
Threshold for termination of iteration.
Concretely, the iteration is stopped when the change of W and variance is smaller than tol.
disp_message : Boolean, default False
If True, the number of iteration and convergence will displayed.
W0 : 2D numpy array, default None
2D numpy array representing the initial value of parameter W
variance0 : positive float, default is None
positive float representing the initial value of parameter variance
'''
self._init_params(X, W=W0, variance=variance0)
for i in range(max_iter):
Wold = self.W
varianceold = self.variance
Ez, sumEzz = self._estep(X)
self._mstep(X, Ez, sumEzz)
err = np.sqrt(np.linalg.norm(self.W - Wold)**2 + (self.variance - varianceold)**2)
if err < tol:
break
if disp_message:
print(f"n_iter : {i}")
print(f"converged : {i < max_iter - 1}")
2.1.7 fit
_fit_analyticalと_fit_emをまとめておきます。
def fit(self, X, method='analytical', **kwargs):
'''
Method for performing fitting
Parameters
----------
X : 2D numpy array
2D numpy array representing input data, where X[n, i] represents the i-th element of n-th point in X.
method : str, either 'analytical' or 'em'
If method == 'analytical', _fit_analytical is invoked, while if method == 'em', _fit_em is invoked.
'''
if method == 'analytical':
self._fit_analytical(X)
elif method == 'em':
self._fit_em(X, **kwargs)
else:
"Method should be either `analytical` or `em`."
2.1.8 transform
PCAによる順方向の変換では、与えられた観測変数$\xi$に対して、潜在変数$\zeta$の分布を返します:
$$
\begin{align}
&{} p\left( \zeta \middle| \xi, X, W, \mu, \sigma^2 \right) = \mathcal{N}\left( \zeta \middle| M^{-1} W^T (\xi - \mu), \sigma^2 M^{-1} \right)
\end{align}
$$
ガウス分布であることは分かっているので、期待値と共分散行列を返すことにします。
以下のコードでは、Xが複数の$\xi$、Zが複数の$\zeta$に対応するものとし、いずれも、$i$番目の行が$i$番目のサンプルに対応するとします。
def transform(self, X, return_cov=False):
'''
Method for performing transformation, transforming observables to latent variables
Parameters
----------
X : 2D numpy array
(len(X), self.d) numpy array representing input data, where X[n, i] represents the i-th element of n-th point in X.
return_cov : Boolean, default False
If True, the covariance matrix of the predictive distribution is also returned
Returns
----------
Z : 2D numpy array
(len(X), self.m) array representing the expectation values of the latent variables
corresponding to the input observable X
cov : 2D numpy array, returned only if return_cov is True
(self.m, self.m) array representing the covariance matrix for the predictive distribution
Concretely, it corresponds to $\sigma^2 M^{-1}$
'''
Minv = np.linalg.inv( (self.W).T @ self.W + self.variance*np.eye(self.m) ) # we only use inverse of the matrix M
dX = X - self.mu
Z = dX @ self.W @ (Minv.T)
if return_cov:
cov = self.variance * Minv
return Z, cov
else:
return Z
2.1.9 inverse_transform
今度は逆に、潜在変数$\zeta$が与えられたときの観測変数$\xi$の分布です:
$$
\begin{align}
&{} p\left( \xi \middle| z, W, \mu, \sigma^2 \right) = \mathcal{N}\left( \xi \middle| W\zeta + \mu, \sigma^2 I_d \right) ,
\end{align}
$$
これも先ほど同様の方針で実装します。
def inverse_transform(self, Z, return_cov=False):
'''
Method for performing inverse transformation, transforming latent variables to observables
Parameters
----------
Z : 2D numpy array
(len(Z), self.m) numpy array representing latent variables
return_cov : Boolean, default False
If True, the covariance matrix of the predictive distribution is also returned
Returns
----------
X : 2D numpy array
(len(Z), self.d) numpy array representing input data, where X[n, i] represents the i-th element of n-th point in X.
cov : 2D numpy array, returned only if return_cov is True
(self.d, self.d) array representing the covariance matrix for the predictive distribution
Concretely, it corresponds to $\sigma^2 I_d$
'''
X = Z @ (self.W.T) + self.mu
if return_cov:
cov = self.variance * np.eye(self.d)
return X, cov
else:
return X
2.1.10 MLPCAクラス全体のコード
以上のコードをまとめて、次のようにMLPCAクラスを定義します。
class MLPCA:
def __init__(self, m):
self.m = m
self.d = None
self.W = None
self.mu = None
self.variance = None
def _fit_analytical(self, X):
self.d = len(X[0])
self.mu = np.mean(X, axis=0)
S = np.cov(X, rowvar=False, ddof=0)
eigenvals, eigenvecs = eigh(S)
ind = np.argsort(eigenvals)[::-1][0:self.m] # sort the eigenvalues in decreasing order, and choose the largest m
eigenvals_largest = eigenvals[ind]
eigenvecs_largest = eigenvecs[:, ind]
if self.d != self.m:
self.variance = 1/(self.d - self.m) * np.sum(np.sort(eigenvals)[::-1][self.m:])
else:
self.variance = 0.0
self.W = eigenvecs_largest @ np.diag( np.sqrt(eigenvals_largest - self.variance) )
def _init_params(self, X, W=None, variance=None):
'''
Method for initializing model parameterse based on the size and variance of the input data array.
Parameters
----------
X : 2D numpy array
2D numpy array representing input data, where X[n, i] represents the i-th element of n-th point in X.
W : 2D numpy array, default None
2D numpy array representing the initial value of parameter W
variance : positive float, default is None
positive float representing the initial value of parameter variance
'''
self.d = len(X[0])
self.mu = np.mean(X, axis=0)
self.W = np.eye(self.d)[:,:self.m] if (W is None) else W # probably there are better initializations
self.variance = 1.0 if (variance is None) else variance
def _estep(self, X):
'''
Method for performing E-step, returning
$\mathbb{E}_{old}\left[ z_n \right]$ and $\sum_{n=0}^{N-1} \mathbb{E}_{old}\left[ z_n z_{n}^{T} \right]$
Parameters
----------
X : 2D numpy array
2D numpy array representing input data, where X[n, i] represents the i-th element of n-th point in X.
Returns
----------
Ez : 2D numpy array
(len(X), self.m) array, where Ez[n, i] = $\mathbb{E}_{old}[z_n]_i$
sumEzz : 2D numpy array
(self.m, self.m) array, where sumEzz[i,j] = $\sum_{n=0}^{N-1} \mathbb{E}_{old}\left[z_n z_{n}^{T} \right]_{i,j}$
'''
Minv = np.linalg.inv( (self.W).T @ self.W + self.variance*np.eye(self.m) ) # we only use inverse of the matrix M
dX = X - self.mu
Ez = dX @ self.W @ (Minv.T)
sumEzz = len(X) * self.variance * Minv + (Ez.T) @ Ez
return Ez, sumEzz
def _mstep(self, X, Ez, sumEzz):
'''
Method for performing M-step, and updating model parameters
Parameters
----------
X : 2D numpy array
2D numpy array representing input data, where X[n, i] represents the i-th element of n-th point in X.
Ez : 2D numpy array
(len(X), self.m) array, where Ez[n, i] = $\mathbb{E}_{old}[z_n]_i$
sumEzz : 2D numpy array
(self.m, self.m) array, where sumEzz[i,j] = $\sum_{n=0}^{N-1} \mathbb{E}_{old}\left[z_n z_{n}^{T} \right]_{i,j}$
'''
dX = X - self.mu
self.W = ((dX.T) @ Ez) @ np.linalg.inv(sumEzz)
self.variance = ( np.linalg.norm(dX)**2 - 2*np.trace(Ez @ (self.W.T) @ (dX.T) ) + np.trace( sumEzz @ self.W.T @ self.W ) ) /(len(X)*self.d)
def _fit_em(self, X, max_iter=100, tol=1e-4, disp_message=False, W0=None, variance0=None):
'''
Method for performing fitting by EM algorithm
Parameters
----------
X : 2D numpy array
2D numpy array representing input data, where X[n, i] represents the i-th element of n-th point in X.
max_iter : positive int
The maximum number of iteration allowed
tol : positive float
Threshold for termination of iteration.
Concretely, the iteration is stopped when the change of W and variance is smaller than tol.
disp_message : Boolean, default False
If True, the number of iteration and convergence will displayed.
W0 : 2D numpy array, default None
2D numpy array representing the initial value of parameter W
variance0 : positive float, default is None
positive float representing the initial value of parameter variance
'''
self._init_params(X, W=W0, variance=variance0)
for i in range(max_iter):
Wold = self.W
varianceold = self.variance
Ez, sumEzz = self._estep(X)
self._mstep(X, Ez, sumEzz)
err = np.sqrt(np.linalg.norm(self.W - Wold)**2 + (self.variance - varianceold)**2)
if err < tol:
break
if disp_message:
print(f"n_iter : {i}")
print(f"converged : {i < max_iter - 1}")
def fit(self, X, method='analytical', **kwargs):
'''
Method for performing fitting
Parameters
----------
X : 2D numpy array
2D numpy array representing input data, where X[n, i] represents the i-th element of n-th point in X.
method : str, either 'analytical' or 'em'
If method == 'analytical', _fit_analytical is invoked, while if method == 'em', _fit_em is invoked.
'''
if method == 'analytical':
self._fit_analytical(X)
elif method == 'em':
self._fit_em(X, **kwargs)
else:
"Method should be either `analytical` or `em`."
def transform(self, X, return_cov=False):
'''
Method for performing transformation, transforming observables to latent variables
Parameters
----------
X : 2D numpy array
(len(X), self.d) numpy array representing input data, where X[n, i] represents the i-th element of n-th point in X.
return_cov : Boolean, default False
If True, the covariance matrix of the predictive distribution is also returned
Returns
----------
Z : 2D numpy array
(len(X), self.m) array representing the expectation values of the latent variables
corresponding to the input observable X
cov : 2D numpy array, returned only if return_cov is True
(self.m, self.m) array representing the covariance matrix for the predictive distribution
Concretely, it corresponds to $\sigma^2 M^{-1}$
'''
Minv = np.linalg.inv( (self.W).T @ self.W + self.variance*np.eye(self.m) ) # we only use inverse of the matrix M
dX = X - self.mu
Z = dX @ self.W @ (Minv.T)
if return_cov:
cov = self.variance * Minv
return Z, cov
else:
return Z
def inverse_transform(self, Z, return_cov=False):
'''
Method for performing inverse transformation, transforming latent variables to observables
Parameters
----------
Z : 2D numpy array
(len(Z), self.m) numpy array representing latent variables
return_cov : Boolean, default False
If True, the covariance matrix of the predictive distribution is also returned
Returns
----------
X : 2D numpy array
(len(Z), self.d) numpy array representing input data, where X[n, i] represents the i-th element of n-th point in X.
cov : 2D numpy array, returned only if return_cov is True
(self.d, self.d) array representing the covariance matrix for the predictive distribution
Concretely, it corresponds to $\sigma^2 I_d$
'''
X = Z @ (self.W.T) + self.mu
if return_cov:
cov = self.variance * np.eye(self.d)
return X, cov
else:
return X
2.2 BPCAクラス
次に、ベイズ的アプローチによる確率主成分分析を行う、BPCAクラスを実装します。先述したように、MLPCAクラスを継承することで定義します。
2.2.1 概要:データ属性とメソッド
MLPCAクラスの持つデータ属性とメソッドに加え、以下のデータ属性とメソッドを持たせます。
データ属性
-
alpha: $\alpha$
メソッド
-
_calc_alpha: $\alpha$の更新を行うメソッド。
また、_init_params, _m_step, fitメソッドをオーバーライドします7。
2.2.2 _init_params
MLPCAで用いたパラメーターに加えて、alphaの初期化も行う必要があるので、オーバーライドしておきます。デフォルトのalphaの初期値は要素が全て1の配列としておきます。また、alpha以外はMLPCAクラスと同様の初期化を行えばよいので、super()を用いることにします。
def _init_params(self, X, W=None, variance=None, alpha=None):
'''
Method for initializing model parameterse based on the size and variance of the input data array.
Parameters
----------
X : 2D numpy array
2D numpy array representing input data, where X[n, i] represents the i-th element of n-th point in X.
W : 2D numpy array, default None
2D numpy array representing the initial value of parameter W
variance : positive float, default is None
positive float representing the initial value of parameter variance
alpha : positive float, default is None
positive float representing the initial value of alpha
'''
super()._init_params(X, W, variance)
self.alpha = np.ones(self.m) if (alpha is None) else alpha
2.2.3 _mstep
ベイズ的アプローチでのM-stepでは、次のように$W$と$\sigma^2$を更新します。
$$
\begin{align}
& W_{new} = \left[ \sum_{n=0}^{N-1} (x_n - \bar{x}) \mathbb{E}_{old}[z_n]^T \right]
\left[ \sum_{n=0}^{N-1} \mathbb{E}_{old}[z_n z_{n}^{T}] + \sigma_{old}^{2} A \right]^{-1} \
& A = \mathrm{diag}\left( \alpha_{i, old} \right) \
& \sigma^{2}_{new} = \frac{1}{ND}\sum_{n=0}^{N-1}
\left[ \| x_n - \bar{x} \|^2 - 2 \mathbb{E}_{old}\left[ z_n\right]^T W_{new}^{T} (x_n-\bar{x})
{} + \mathrm{Tr}\left( \mathbb{E}_{old}\left[ z_n z_{n}^{T} \right] W_{new}^{T} W_{new} \right) \right]
\end{align}
$$
これをコードに翻訳すると以下の通りです
def _mstep(self, X, Ez, sumEzz):
'''
Method for performing M-step, and updating model parameters
Parameters
----------
X : 2D numpy array
2D numpy array representing input data, where X[n, i] represents the i-th element of n-th point in X.
Ez : 2D numpy array
(len(X), self.m) array, where Ez[n, i] = $\mathbb{E}_{old}[z_n]_i$
sumEzz : 2D numpy array
(self.m, self.m) array, where sumEzz[i,j] = $\sum_{n=0}^{N-1} \mathbb{E}_{old}\left[z_n z_{n}^{T} \right]_{i,j}$
'''
dX = X - self.mu
self.W = ((dX.T) @ Ez) @ np.linalg.inv(sumEzz + self.variance * np.diag(self.alpha))
self.variance = ( np.linalg.norm(dX)**2 - 2*np.trace(Ez @ (self.W.T) @ (dX.T) ) + np.trace( sumEzz @ self.W.T @ self.W ) ) /(len(X)*self.d)
2.2.4 _calc_alpha
次に、alphaの更新を行うメソッドを実装します。alphaの更新式は、
$$
\begin{align}
& \alpha_{i,new} = \frac{d}{\|w_{i,new}\|^2}
\end{align}
$$
でした。$\|w_i \|$が0になったときの処理をどうするかやや悩むところではありすが、ここでは対応する$\alpha_i$を単純にnp.infで置き換えることにします。
def _calc_alpha(self):
'''
Method for updating the value of alpha for Bayesian approach
'''
wnorms = np.linalg.norm(self.W, axis=0)**2
for i in range(self.m):
self.alpha[i] = self.d/wnorms[i] if (wnorms[i] != 0) else np.inf
2.2.5 fit
最後に、学習を行うためのメソッドを定義します。
最尤法のEMアルゴリズムの場合と同様に、$W$と$\sigma^2$の変化が十分小さくなったら停止することにします。$\alpha$は一部が無限大になることが期待されるので、収束判定には含めません8。
def fit(self, X, max_iter=100, tol=1e-4, disp_message=False, W0=None, variance0=None, alpha0=None):
'''
Method for performing fitting
Parameters
----------
X : 2D numpy array
2D numpy array representing input data, where X[n, i] represents the i-th element of n-th point in X.
max_iter : positive int
The maximum number of iteration allowed
tol : positive float
Threshold for termination of iteration.
Concretely, the iteration is stopped when the change of W and variance is smaller than tol.
disp_message : Boolean, default False
If True, the number of iteration and convergence will displayed.
W0 : 2D numpy array, default None
2D numpy array representing the initial value of parameter W
variance0 : positive float, default is None
positive float representing the initial value of parameter variance
alpha0 : positive float, default is None
positive float representing the initial value of alpha
'''
self._init_params(X, W=W0, variance=variance0, alpha=alpha0)
for i in range(max_iter):
Wold = self.W
varianceold = self.variance
Ez, sumEzz = self._estep(X)
self._mstep(X, Ez, sumEzz)
self._calc_alpha()
# convergence check. because we expect some components of alpha to be infinite, alpha is excluded from the convergence criterion
err = np.sqrt(np.linalg.norm(self.W - Wold)**2 + (self.variance - varianceold)**2)
if err < tol:
break
if disp_message:
print(f"n_iter : {i}")
print(f"converged : {i < max_iter - 1}")
2.2.6 BPCAクラス全体のコード
以上をまとめると、BPCAクラスは次のように定義できます
class BPCA(MLPCA):
def __init__(self, m):
super().__init__(m)
self.alpha = None
def _init_params(self, X, W=None, variance=None, alpha=None):
'''
Method for initializing model parameterse based on the size and variance of the input data array.
Parameters
----------
X : 2D numpy array
2D numpy array representing input data, where X[n, i] represents the i-th element of n-th point in X.
W : 2D numpy array, default None
2D numpy array representing the initial value of parameter W
variance : positive float, default is None
positive float representing the initial value of parameter variance
alpha : positive float, default is None
positive float representing the initial value of alpha
'''
super()._init_params(X, W, variance)
self.alpha = np.ones(self.m) if (alpha is None) else alpha
def _mstep(self, X, Ez, sumEzz):
'''
Method for performing M-step, and updating model parameters
Parameters
----------
X : 2D numpy array
2D numpy array representing input data, where X[n, i] represents the i-th element of n-th point in X.
Ez : 2D numpy array
(len(X), self.m) array, where Ez[n, i] = $\mathbb{E}_{old}[z_n]_i$
sumEzz : 2D numpy array
(self.m, self.m) array, where sumEzz[i,j] = $\sum_{n=0}^{N-1} \mathbb{E}_{old}\left[z_n z_{n}^{T} \right]_{i,j}$
'''
dX = X - self.mu
self.W = ((dX.T) @ Ez) @ np.linalg.inv(sumEzz + self.variance * np.diag(self.alpha))
self.variance = ( np.linalg.norm(dX)**2 - 2*np.trace(Ez @ (self.W.T) @ (dX.T) ) + np.trace( sumEzz @ self.W.T @ self.W ) ) /(len(X)*self.d)
def _calc_alpha(self):
'''
Method for updating the value of alpha for Bayesian approach
'''
wnorms = np.linalg.norm(self.W, axis=0)**2
for i in range(self.m):
self.alpha[i] = self.d/wnorms[i] if (wnorms[i] != 0) else np.inf
def fit(self, X, max_iter=100, tol=1e-4, disp_message=False, W0=None, variance0=None, alpha0=None):
'''
Method for performing fitting
Parameters
----------
X : 2D numpy array
2D numpy array representing input data, where X[n, i] represents the i-th element of n-th point in X.
max_iter : positive int
The maximum number of iteration allowed
tol : positive float
Threshold for termination of iteration.
Concretely, the iteration is stopped when the change of W and variance is smaller than tol.
disp_message : Boolean, default False
If True, the number of iteration and convergence will displayed.
W0 : 2D numpy array, default None
2D numpy array representing the initial value of parameter W
variance0 : positive float, default is None
positive float representing the initial value of parameter variance
alpha0 : positive float, default is None
positive float representing the initial value of alpha
'''
self._init_params(X, W=W0, variance=variance0, alpha=alpha0)
for i in range(max_iter):
Wold = self.W
varianceold = self.variance
Ez, sumEzz = self._estep(X)
self._mstep(X, Ez, sumEzz)
self._calc_alpha()
# convergence check. because we expect some components of alpha to be infinite, alpha is excluded from the convergence criterion
err = np.sqrt(np.linalg.norm(self.W - Wold)**2 + (self.variance - varianceold)**2)
if err < tol:
break
if disp_message:
print(f"n_iter : {i}")
print(f"converged : {i < max_iter - 1}")
3 実験
では、実装したMLPCA, BPCAクラスを動かしてみましょう。
ここでは、3つのデータを使います。
- 2次元ガウス分布:簡単なトイデータです。$d=2$なので、必然的に$m=1$となります。最尤法の解析解とEMアルゴリズムが一致するのかと、最尤法とベイズ的アプローチにどの程度の差が出るのかを見ます。
- 高次元ガウス分布:次に10次元のガウス分布から生成されたデータを扱います。3つの方向に分散1.0, 残りの方向に分散0.1を持つとします。ベイズ的アプローチにより、適切な$m$の値を自動で選べるかどうかを見ます。
- 手書き数字:最後に、より実際的なデータを扱います。さきほどの高次元ガウス分布の場合と同様に、ベイズ的アプローチが実効的な次元を下げるかを見ます。
3.1 2次元Gauss分布
rnd = np.random.RandomState(0)
X = rnd.multivariate_normal(np.zeros(2), cov = np.array([[2,1],[1,2]]), size=200)
$d=2$なので、先述したように、$m$の値は必然的に1となります。この設定で、
- 最尤法の解析解
- 最尤法のEMアルゴリズムによる解
- ベイズ的アプローチによる解
を比較してみましょう。
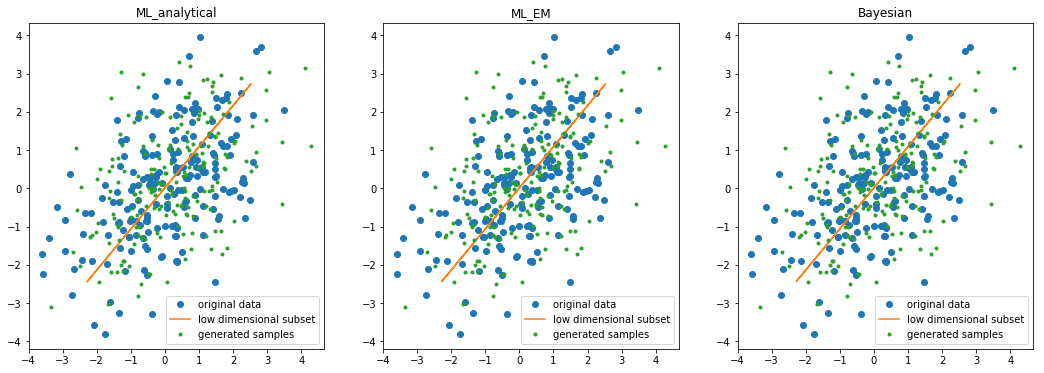
具体的には、次の2つの比較を行います。
- $C=W W^T + \sigma^2 I_d$の値。なお、$W$を直接比べても意味がない9ことに注意。
- 生成されるデータをプロットする。
まず、 $C$の比較です:
The difference between C_analytical and C_em : 2.6651931942223766e-06
The difference between C_analytical and C_b : 0.04384689691566826
期待されたとおり、EMアルゴリズムと解析解の間にはほぼ差がないようです。また、ベイズ的アプローチの結果ともさは大きくないようです。
次に、inverse_transformを使ってデータを生成し、プロットしてみましょう10。
元のデータ、PCAによって抽出される低次元の部分集合、生成されるデータをプロットしてみました。いずれの観点からも、これら3つのPCAの間に目で見て分かるほどの違いはないようです。
3.2 高次元データ
次に、より高次元のデータを扱ってみましょう。最尤法については解析解のみを考えることにし、ベイズ的アプローチとどのような違いが現れるかを比較することにします。
データは$d=10$とし、3方向には分散1.0, 残り7方向には分散0.1とします。
具体的には以下のXを用います11。
N = 300
d = 10
var = np.array([1.0, 0.1, 1.0, 0.1, 0.1, 0.1, 0.1, 0.1, 1.0, 0.1])
rnd = np.random.RandomState(0)
X = rnd.multivariate_normal(np.zeros(d), cov=np.diag(var), size=N)
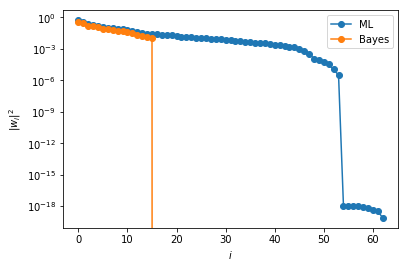
$m=9$とおいたMLPCAクラスとBPCAクラスをこのデータで学習させ、得られた$W$に対する$\|w_i\|^2$をsortしてプロットしたものが次の図です:
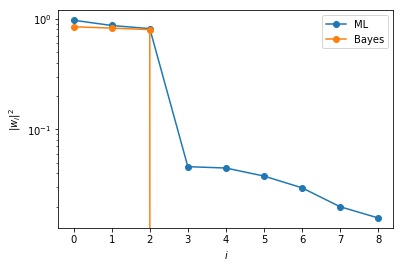
図からも明らかに分かるように、ベイズ的アプローチの場合には、余分な自由度が自動的に抑えられています。
3.3 手書き数字
最後に、手書き数字のデータを用いて、同様の性質が見られるかを試してみましょう。
手書き数字の「3」のデータを用います。
from sklearn import datasets
digits = datasets.load_digits()
threes = digits.data[np.where(digits.target==3)]/16.0 # extracting the data corresponding threes, and perform scaling
print(f"The number of data points : {len(threes)}")
print(f"The dimension of the observables : {len(threes[0])}")
$N=183, d=64$です。
The number of data points : 183
The dimension of the observables : 64
具体的にいくつかの例をプロットしたものが、以下の図です:
$m=63$とおいたMLPCAクラスとBPCAクラスをこのデータで学習させ、得られた$W$に対する$\|w_i\|^2$をsortしてプロットしたものが次の図です:
このデータに対しても、ベイズ的アプローチでは、余分な自由度が大きく削ぎ落とされていることが見て取れます。
4 まとめ
この章では、最尤法とベイズ的アプローチの、2種類の確率的主成分分析を実装しました。実験から、ベイズ的アプローチは余計な自由度を削ぎ落とすという振る舞いが見られました。これにより、「$m$の値を事前に人手で選ぶのではなく、($m=d-1$と置いてから学習を行うことにより)自動で適切な$m$の値を選ぶことができる」というのが、ベイズ的アプローチの大きな利点だと(PRMLや原論文で)述べられています。
ただ、この点については筆者はあまり理解できていません。
というのも、有効次元数12が$m$に依存してしまう振る舞いが実験で見られたからです。たとえば手書き数字の例では、m=63では有効次元数は15程度でしたが、m=30では有効次元数10以下になります。これは上記の直感的な説明とはどうも符合しないように感じられます13。
この問題の理解は、ひとまず今後の課題としたいと思います。
-
$\mu, \sigma^2$には事前分布をおいていないので完全にベイズ的ではないのですが、ここでは以下のモデルを用いた確率的主成分分析を、ベイズ的アプローチよるものと呼ぶことにします。 ↩
-
潜在空間での回転の任意性を表す$R$は、ここでは外します(なくても結果は等価なので。)。 ↩
-
$M$の値や、反復回数にも依存するので、「必ず計算が速くなります」とは言い切れないかと思います。 ↩
-
どのような条件下でこの近似が正当化されるか、筆者はきちんとは理解していません。。。 ↩
-
この更新式はEMアルゴリズムそのものではありません。というのも、$\alpha$に対する更新も同時に行うからです。この更新式の妥当性や収束性などについては、筆者は理解できていません。。。 ↩
-
正確には、$M$は常に正則とは限りません(たとえば、$N=2, d=3, m=2, x_0 = (1, 0, 0)^T, x_1 = (-1, 0, 0)$とし、このデータに対して最尤推定を行うと、得られる$M$は非正則になります。)。このとき、順方向の変換を行うとエラーが発生します。ただし、逆変換は問題なく行えます。確率的モデルを考えないconventionalなPCAでは、この問題は起きません。 ↩
-
_estepの数式は、最尤推定のときと同一であることに注意。 ↩ -
逆数をとって考えれば、収束判定に入れても良いかもしれません。ただ、
alphaの更新式を見れば分かるように、$\alpha_i$の逆数は$\|w_i\|^2/d$です。既に$W$の変化は収束判定に使われているので、冗長かと思い省きました。 ↩ -
モデルの定義よりすぐ分かるように、潜在空間での回転の分の任意性があります。 ↩
-
random stateは3つの場合に対して共通のものをとっています。 ↩
-
独立なGauss分布だとあまりにも綺麗なので、適当に回転させたほうがよいかもしれません。 ↩
-
ここでは、$\|w_i\|^2 \neq 0$となる$i$の個数、とします(より正しくは、数値誤差を考慮して、ある閾値を用意してそれ以下のものを0と判定する、とすべきですが)。 ↩
-
実装のバグによるもの、という可能性も否定できないのですが、私には見つけられませんでした。。。もしバグがあれば、指摘を歓迎いたします。 ↩