この記事では、PRML第6章で述べられている、ガウス過程回帰を実装します。
対応するjupyter notebookは筆者のgithubリポジトリにあります。連載全体の方針や、PRMLの他のアルゴリズムの実装については、連載のまとめページをご覧いただければと思います。
1 理論のおさらい
まず、PRMLで述べられている記号や式をざっくり復習しましょう。ちょっと記号をPRMLから変えてありますが、PRMLの中身を理解している方は、ここを飛ばして2節に進んでしまって大丈夫です。
途中計算1がややいかつい章ですが、ガウス過程回帰は本質的には「ベイジアン線型回帰の一種で、priorとしてガウス過程を用いたもの」と捉えると分かりやすいかと思います。
1.1 設定
- $N \in \mathbb{N}$ : 訓練データの個数
- $d \in \mathbb{N}$ : 入力の次元
- 訓練データのうち、入力の部分を$x_0, x_1, \dots , x_{N-1} \in \mathbb{R}^d$、ラベル(出力、目的値)を$t_0, t_1, \dots, t_{N-1} \in \mathbb{R}$とします。今回は回帰問題を考えるので、$t_i$は実数値ですね。また、ラベルをまとめて$t := (t_0, \dots, t_{N-1})^T \in \mathbb{R}^N$と表すことにします。
1.2 ガウス過程
先ほども述べたように、ガウス過程回帰では、ガウス過程をベイジアン線型回帰の事前分布として用います。そこで、回帰問題を考える前に、まずガウス過程そのものについてざっと見ておきましょう。
1.2.1 定義
ガウス過程とは、ある集合$X$上の実数値函数上に値をとる確率変数で、次の条件を満たすものをさします2:
ある$\mu : X \rightarrow \mathbb{R}$と$k : X \times X \rightarrow \mathbb{R}$が存在し、任意の$N \in \mathbb{N}$と任意の$x_0, \dots, x_{N-1} \in X$に対し、ガウス過程で得られる函数$y : X \rightarrow \mathbb{R}$の$x_0, \dots, x_{N-1}$における値$y(x_0), \dots, y(x_{N-1})$が確率密度
$$
\begin{align}
p\left(y(x_0), y(x_1), \dots, y(x_{N-1}) \middle| \mu,k \right)
= \mathcal{N}\left((y(x_0), y(x_1), \dots, y(x_{N-1}) )^T \middle| M, K \right),
\end{align}
$$
に従う。ただし、
$$
\begin{align}
\mathcal{N} &: \mbox{ ガウス分布の確率密度} \
M &:= \left(\mu(x_0), \mu(x_1), \dots, \mu(x_{N-1}) \right)^T \ \ \in \mathbb{R}^N \
K &:= \left( K_{i,j} \right)_{i,j = 0, \dots, N-1}, \ \ K_{i,j} = k(x_i, x_j),
\mbox{ $K$は正定値 }
\end{align}
$$
ここで出てきた函数$k$をカーネル函数、行列$K$をカーネル行列(またはグラム行列)と呼びます。
1.2.2 平均と分散
上記の確率密度函数より、
$$
\begin{align}
& \mathbb{E}[y(x_n)] = M_n \
& \mathbb{E}\left[\left(y(x_n)-M_n \right) \left( y(x_m) - M_m\right) \right] = K_{n,m}
\end{align}
$$
が従います。つまり、$\mu$は平均、$k$は共分散を与えるわけです。応用上は、$M = 0$とすることが多いとのことですので、この記事でも以後は$\mu$は常に0を与える函数と仮定します。
この定義は全くもって数学的に厳密なものではありません。ただ、実用上は有限個の点しか考えないので、上記の定義で問題なくガウス過程を利用できるかと思います3。
1.3 ガウス過程回帰
いよいよ、ガウス過程回帰です。既に聞き飽きたかと思いますが、ガウス過程回帰は本質的には、「ガウス過程を事前分布に用いたベイジアン線型回帰」です。ガウス過程の確率密度関数は与えてあるので、この節では尤度を与え、これらから予測分布を導出します。また、3章のベイジアン線型回帰でエビデンス近似を行ったように、エビデンス(周辺尤度)を最大化するハイパーパラメーターを自動で決める方法も述べます。
1.3.1 尤度
入力$x_n$とガウス過程で決まる函数$y$が与えられたとき、出力(ラベル)$t_n$は次の確率密度に従うとします。
$$
\begin{align}
p\left(t_n \middle| y(x_n) \right) = \mathcal{N}\left(t_n \middle| y(x_n), \beta^{-1} \right),
\end{align}
$$
つまり、$t_n$は$y(x_n)$にガウスノイズが加わったものとなります。
ノイズが独立と仮定すると、次のモデルが得られます。
$$
\begin{align}
p \left( t\middle| y \right) = \mathcal{N} \left( t \middle| y, \beta^{-1} I_N \right) ,
\end{align}
$$
ただし、記法を簡単にするために、$y := (y(x_0), y(x_1), \dots, y(x_{N-1}))^T$としました4。また、$I_N$は$N$次元単位行列です。
1.3.2 予測分布
事前分布と尤度を与えたので、ここから予測分布を求めることができます。
正確には:$N$点の訓練データ$(x_0, t_0), (x_1, t_1), \dots, (x_{N-1},t_{N-1})$が与えられたとき、新しい入力$\xi$に対する出力$\tau$の値の分布を求めます5。
$$
\begin{align}
t &:= (t_0, t_1, \dots, t_{N-1})^T \
t' &:= (t_0, t_1, \dots, t_{N-1}, \tau)^T
\end{align}
$$
と表すと、今求めたい確率(密度)は、$p(\tau| t )$と表せます(入力$x_0, x_1, \dots, x_{N-1}, \xi$はいったん固定されているとするので、ここでは省略します。)。
この確率を求めるために、まず同時分布$p(t')$を求めます。次に、$t$について条件づけを行い、$p(\tau| t )$を求めます。
まず同時分布は以下の通りです(PRML (6.61), (6.64)。これらの式はPRML(2.115)から導出できます。):
$$
\begin{align}
p(t') &= \mathcal{N}(t'| 0, C'), \
C_{N+1} &=
\begin{pmatrix}
C & \kappa \
\kappa^T & k(\xi, \xi) + \beta^{-1}
\end{pmatrix}, \
\kappa &\in \mathbb{R}^{N}, \ \ \kappa_n = k(\xi, x_n) \
C &:= K + \beta^{-1} I_{N}
\end{align}
$$
これより、条件つき確率は次のようになります(PRML (6.67), (6.68)。これは、PRML(2.81), (2.82)から導出できます。):
$$
\begin{align}
p(\tau | t ) &= \mathcal{N} (\tau | m(\xi), \sigma^2(\xi)), \
m(\xi) &:= \kappa^T C^{-1} t, \
\sigma^2(\xi) &:= k(\xi, \xi) + \beta^{-1} - \kappa^T C^{-1} \kappa
\end{align}
$$
1.4 ハイパーパラメーター最適化
ここまでは、カーネル函数と$\beta$は与えられたものと仮定してきました。
しかし、実際の応用では、適切な$\beta$とカーネル函数を上手く選ぶ必要があります。これを手で行うのは困難ですが、この節ではこれをデータから自動で行う手法について述べます。具体的には、周辺尤度を最大化するハイパーパラメーターを選ぶことにします。なお、ここでは「ハイパーパラメーター」は、カーネルに含まれるパラメーターと$\beta$を併せたものを指すとします。PRMLの本の方には明確には述べられていませんが、ここでは$\beta$も同時に最適化します。
1.4.1 周辺尤度
カーネルのパラメーターを$\theta$と表すことにします。
周辺尤度$p(t|\beta, \theta)$は
$$
\begin{align}
& p(\boldsymbol{t}|\beta, \theta) = \mathcal{N}(\boldsymbol{t} | 0, C) \
& C = K + \beta^{-1} I_N
\end{align}
$$
と表せます(PRML(6.61), (6.62)式)。
従って、対数尤度函数は
$$
\begin{align}
\log p(t|\beta, \theta) = -\frac{1}{2} \log ({\rm det} C)
-\frac{1}{2} t^T C^{-1} t -\frac{N}{2} \log (2\pi)
\end{align}
$$
と表せます。
これを$\beta$と$\theta$の函数とみなし、最大化します。
1.4.2 勾配
対数尤度の最大化にあたって、その勾配の情報も利用することにします。
カーネルパラメーターについての勾配は、
$$
\begin{align}
\frac{\partial}{\partial \theta_i} \log p(t|\beta, \theta)
= -\frac{1}{2} \mathrm{Tr} \left(C^{-1} \frac{\partial C}{\partial \theta_i} \right) + \frac{1}{2} t^T C^{-1} \frac{\partial C}{\partial \theta_i} C^{-1} t
\end{align}
$$
で与えられます。$\beta$についての勾配も全く同様です。
$C$の定義より
$$
\begin{align}
\frac{\partial C}{\partial \theta_i} &= \frac{\partial K}{\partial \theta_i} \
\frac{\partial C}{\partial \beta} &= - \frac{1}{\beta^2} I_N
\end{align}
$$
となります。後のコードでは、この表式を用います。
2 数式からコードへ
ここまで述べてきた数式を、コードに翻訳していきます。
まず、カーネル函数を表すクラスを定義します。これを利用して、ガウス過程回帰を行うクラスを定義します。
これらを別々に定義することにより、様々なカーネル函数を用いたガウス過程回帰を容易に行うことができます6。
2.1 カーネル函数
2.1.1 概要
scikit-learnでのkernelの書き方(こちらの公式ドキュメントを参照)に倣い、ここではMyKernelクラスを、以下のデータ属性とメソッドを持つクラスとして定義します(正確には、後で定義するGPRegressionクラスがカーネル函数として利用できるクラスは、以下のデータ属性とメソッドを持つと仮定します。):
- データ属性
-
theta: 1次元numpy配列で、カーネル函数のパラメーターを表します。 -
bounds: リスト(2次元リスト)。 パラメーターの下限と上限を表します。具体的には、次のような形とします:boundsの第i要素はbounds[i] = [a_i, b_i]と書け、a_iとb_iはどちらも実数で、それぞれi番目のパラメーターの下限と上限を表すとします。
-
- メソッド
-
__call__: カーネル行列を計算するメソッドとします。具体的には、(n_x, d) numpy配列Xと(n_y, d)numpy配列Yが与えられたとき、MyKernel(X,Y)は(n_x, n_y) numpy配列を返し、MyKernel(X,Y)[i_x, i_y]= $k($X[i_x],Y[i_y]$)$となるとします。また、__call__メソッドは引数として、eval_gradientを受け取るとします。eval_gradient = Trueのとき、カーネル行列に加えて、その勾配も返すとします。 -
diag: カーネル行列の対角成分を返します。カーネル行列全体を計算してからその対角成分を抜き出すこともできますが、はじめから対角成分のみを計算するほうが効率が良いため、__call__とは別にこのメソッドを定めることにします7。
-
2.1.2 カーネル函数の具体形
ここでは、カーネル函数の具体的な形としては、PRML(6.63)式のものを用います:
$$
\begin{align}
k_{\theta}(x, y) = \theta_0 \exp\left( -\frac{\theta_1}{2} \| x - y \|^2 \right) + \theta_2 + \theta_3 x^T y
\end{align}
$$
ただし、カーネルのパラメーター$\theta_0, \theta_1, \theta_2, \theta_3$は非負とします8。
このカーネル函数に対して、その勾配は以下のようになります:
$$
\begin{align}
\frac{\partial}{\partial \theta_0} k_{\theta}(x,y) &= \exp\left( -\frac{\theta_1}{2} \| x - y \|^2 \right) \
\frac{\partial}{\partial \theta_1} k_{\theta}(x,y) &= -\frac{\theta_0}{2} \| x - y \|^2 \exp\left( -\frac{\theta_1}{2} \| x - y \|^2\right) \
\frac{\partial}{\partial \theta_2} k_{\theta}(x,y) &= 1 \
\frac{\partial}{\partial \theta_3} k_{\theta}(x,y) &= x^T y
\end{align}
$$
2.1.3 コード
以上の設計と数式を元に、以下にMyKernelクラスを定義します:
class MyKernel:
def __init__(self, theta, bounds=None):
self.theta = theta
self.bounds = bounds
def __call__(self, X, Y, eval_gradient=False):
'''
This method calcualtes the kernel matrix for input points.
Parameters
----------
X, Y : 2-D numpy array
numpy array representing input points. X[n, i] (resp. Y[n, i]) represents the i-th element of n-th point in X (resp Y).
eval_gradientt : bool
If True, the gradient of the kernel matrix w.r.t. to parameters are also returned.
Returns
----------
K : 2-D numpy array, shape = (len(X), len(Y))
numpy array representing the kernel matrix. K[i, j] stands for k(X[i], Y[j])
gradK : 3-D numpy array, shape = (len(self.theta), len(X), len(Y)), optional
numpy array representing the gradient of kernel matrix. gradK[l, m, n] = derivative of K[m, n] w.r.t. self.theta[l]
Returned only if return_std is True.
'''
tmp = np.reshape(np.sum(X**2,axis=1), (len(X), 1)) + np.sum(Y**2, axis=1) -2 * (X @ Y.T)
K = self.theta[0]*np.exp(-self.theta[1]/2*tmp) + self.theta[2] + self.theta[3]*(X @ Y.T)
if not(eval_gradient):
return K
else:
gradK = np.zeros((len(self.theta), len(X), len(Y)))
gradK[0] = np.exp(-self.theta[1]/2*tmp)
gradK[1] = -self.theta[0]/2*tmp*np.exp(-self.theta[1]/2*tmp)
gradK[2] = np.ones((len(X), len(Y)))
gradK[3] = X @ Y.T
return K, gradK
def diag(self, X):
'''
This method calculates the diagonal elements of the kernel matrix.
Parameters
----------
X : 2-D numpy array
numpy array representing input points. X[n, i] represents the i-th element of n-th point in X.
Returns
----------
diagK : 1-D numpy array
numpy array representing the diagonal elements of the kernel matrix. diagK[n] = K[n, n]
'''
diagK = self.theta[0] + self.theta[2] + self.theta[3]*np.sum(X**2, axis=1)
return diagK
2.2 ガウス過程回帰
この節では、ガウス過程回帰を行うGPRegressionクラスを実装します。
2.2.1 概要
GPRegressionには、以下のデータ属性を持たせることにします:
-
kernel: カーネル函数を表すオブジェクト。theta,bounds属性と、__call__、diagメソッドを持つものとします。 -
beta: ノイズの精度パラメーター。 -
X_train: 訓練データの入力部分。予測を行う際に使用します。 -
t_train: 訓練データのラベル部分。予測を行う際に使用します。 -
Cinv: $C^{-1}$. 予測の際に用いるので、学習の際に計算して、保持するようにしておきます。
また、次のメソッドを持つものとします:
-
fit: 学習を行うメソッド。Cinvを訓練データから計算し、保持します。引数のoptimize_hparamsがTrueのときは、まずハイパーパラメーターの最適化を行い、その後Cinvを計算します。 -
predict: 予測を行うメソッド。引数のreturn_stdがTrueのとき、予測標準偏差も返します。
また、ハイパーパラメーター最適化のために、コスト函数(と勾配)を返す函数cost_and_gradをGPRegressionとは別に定義しておきます。
2.2.2 学習(ハイパーパラメーター固定)
ハイパーパラメーターが固定のとき、学習で行うのは$C^{-1}$(Cinv)の計算だけです。
具体的には、
$$
\begin{align}
& C = K + \beta^{-1} I_N \
& K := \left( K_{i,j} \right)_{i,j = 0, \dots, N-1}, \ \ K_{i,j} = k(x_i, x_j),
\end{align}
$$
を実装するだけなので、これはそのまんまですね。
2.2.3 予測
入力$\xi$に対するラベル$\tau$の予測分布は、
$$
\begin{align}
p(\tau | t ) &= \mathcal{N} (\tau | m(\xi), \sigma^2(\xi)), \
m(\xi) &:= \kappa^T C^{-1} t, \
\sigma^2(\xi) &:= k(\xi, \xi) + \beta^{-1} - \kappa^T C^{-1} \kappa \
\kappa &\in \mathbb{R}^N, \ \ \kappa_n := k(\xi, x_n)
\end{align}
$$
で与えられました。
これは1つの入力$\xi$に対する分布の表式ですが、実用上は複数の点$\xi_i$ ($i=0, \dots, N_{test}-1$)に対して、$m(\xi_i), \sigma(\xi_i)$を一括で計算することが多いかと思います9。そこで、ここではpredictをそのようなメソッドとして実装する準備をします。
まず、以下の配列を定義します。
-
mean: ($N_{test}$, ) numpy配列。mean[i]= $m(\xi_i)$ -
std: ($N_{test}$, ) numpy配列。std[i]= $\sigma(\xi_i)$ -
kappa: ($N_{test}, N$) numpy配列。kappa[i, j]= $k(\xi_i, x_j)$
すると、
-
mean[i] = $\sum_{j, k}$kappa[i, j]$\left( C^{-1} \right)_{j, k} t_k$ - (
std[i])**2 = $k(\xi_i, \xi_i) + \beta^{-1} - \sum_{j, k}$kappa[i, j]$\left(C^{-1} \right)_{j,k} $kappa[i, k]
となります。predictメソッドの実装には、この表式を用います。
2.2.4 ハイパーパラメーター最適化
対数尤度とその勾配は
$$
\begin{align}
\log p(t|\beta, \theta) &= -\frac{1}{2} \log ({\rm det} C)
-\frac{1}{2} t^T C^{-1} t -\frac{N}{2} \log (2\pi) \
\frac{\partial}{\partial \theta_i} \log p(t|\beta, \theta)
&= -\frac{1}{2} \mathrm{Tr} \left(C^{-1} \frac{\partial C}{\partial \theta_i} \right) + \frac{1}{2} t^T C^{-1} \frac{\partial C}{\partial \theta_i} C^{-1} t \
C &= K + \beta^{-1} I_N
\end{align}
$$
で与えられます。
この節では、コスト函数(対数尤度の負符号を取ったもの)とその勾配を求める関数を定義しておきます。最適化の実行には、後でscipy.optimize.minimizeを用いるので、負符号をつけておきます。
なお、$\log(\mathrm{det}C)$の計算では、underflowを防ぐために一工夫を加えます。直接determinantを計算するのではなく、$C$の固有値を用います。具体的には、$\lambda_i$ $(i= 0, \dots, N-1)$を固有値として、
$$
\begin{align}
\log(\mathrm{det}C)
= \log \left( \prod_{i=0}^{N-1} \lambda_i \right)
= \sum_{i=0}^{N-1} \log \lambda_i
\end{align}
$$
のように計算します。固有値を求めるにあたっては、scipy.linalg.eighを用いました。
非常に小さい値のdetを計算してからlogを取るのではなく、logを取ってから和を取ることによって、underflowを防ぎます。
なお、この一工夫を行わずにnp.linalg.detを使って計算したときは、最適化が失敗するケースが多々ありました。)。
def cost_and_grad(beta, theta, kernel, X, t, return_grad=False):
'''
The method calculates cost function (negative of log marginal likelihood) and its gradient
Parameters
----------
beta : float
noise parameter (precision)
theta : 1-D numpy array
1-D numpy array representing kernel parameteres
kernel : kernel object
An object representing kernel function
X : 2-D numpy array
Array representing input data, with X[n, i] being the i-th element of n-th point in X.
t : 1-D numpy array
Array representing label data.
return_grad : bool
If True, the function also returns the gradient of the cost function.
Returns
----------
val : float
The value of the cost function
grad : 1-D numpy array, optional
Array representing the gradient of the cost function. Returned only if return_grad is True.
'''
kernel.theta = theta
K, gradK = kernel(X, X, eval_gradient=True)
C = K + 1.0/beta*np.identity(len(K))
Cinv = np.linalg.inv(C)
val = np.sum(np.log(eigh(C)[0])) + 0.5 * t @ Cinv @ t + 0.5*len(X)*np.log(2*np.pi)
if not(return_grad):
return val
else:
grad = np.zeros(len(theta)+1)
grad[0] = -0.5*np.trace(Cinv)/(beta**2) + 0.5/(beta**2) * (t @ Cinv @ Cinv @ t)
for cnt in range(len(theta)):
grad[cnt+1] = 0.5 * np.trace(Cinv @ gradK[cnt]) - 0.5 * t @ Cinv @ gradK[cnt] @ Cinv @ t
return val, grad
2.2.5 コード
ここまでのもろもろを組み合わせて、GPRegressionクラスを以下のように定義します。
class GPRegression:
def __init__(self, kernel, beta):
self.kernel = kernel
self.beta = beta
def fit(self, X, t, optimize_hparams=False):
'''
Parameters
----------
X : 2-D numpy array
Array representing training input data, with X[n, i] being the i-th element of n-th point in X.
t : 1-D numpy array
Array representing training label data.
optimize_hparams : bool
If True, optimization of hyperparameters (noise parameter and kernel parameters) is performed.
'''
self.X_train = X
self.t_train = t
if optimize_hparams:
theta_old = np.copy(self.kernel.theta)
bounds_full = np.concatenate(( [[0, None]], self.kernel.bounds ), axis=0)
result = minimize(x0=np.append([self.beta], [self.kernel.theta]),
fun=lambda x : cost_and_grad(beta=x[0], theta=x[1:], kernel=self.kernel, X=self.X_train, t=self.t_train, return_grad=True),
jac=True,
bounds=bounds_full)
if not(result.success):
print(result.message)
self.kernel.theta = theta_old
else:
print(result.message)
self.beta = result.x[0]
self.kernel.theta = result.x[1:]
self.Cinv = np.linalg.inv( self.kernel(self.X_train, self.X_train) + 1.0/self.beta*np.identity(len(self.X_train)) )
def predict(self, X, return_std=False):
'''
Parameters
----------
X : 2-D numpy array
Array representing test input data, with X[n, i] being the i-th element of n-th point in X.
return_std : bool
If True, predictive standard deviation is also returned.
Returns
----------
mean : 1-D numpy array
Array representing predictive mean.
std : 1-D numpy array, optional
Array reprensenting predictive standard deviation, returned only if return_std is True.
'''
kappa = self.kernel(X, self.X_train)
mean = kappa @ (self.Cinv @ self.t_train)
if not(return_std):
return mean
else:
std = np.sqrt( self.kernel.diag(X) + 1.0/self.beta - np.diag( kappa @ self.Cinv @ (kappa.T) ) )
return mean, std
3 実験
では、ここまで書いてきたコードを動かします!
この記事では、$d=1$の例を扱います。
3.1 ガウス過程とカーネル函数
回帰を行う前にまず、ガウス過程でどのような函数が得られるか、特に、カーネル函数のパラメーターを変えたときにどのような影響が出るかを見てみましょう。
カーネル函数の形を再掲しておきます。
$$
\begin{align}
k_{\theta}(x, y) = \theta_0 \exp\left( -\frac{\theta_1}{2} \| x - y \|^2 \right) + \theta_2 + \theta_3 x^T y
\end{align}
$$
各パラメーターの組に対して、5つのサンプル10を生成してプロットしたものが、以下の図になります。
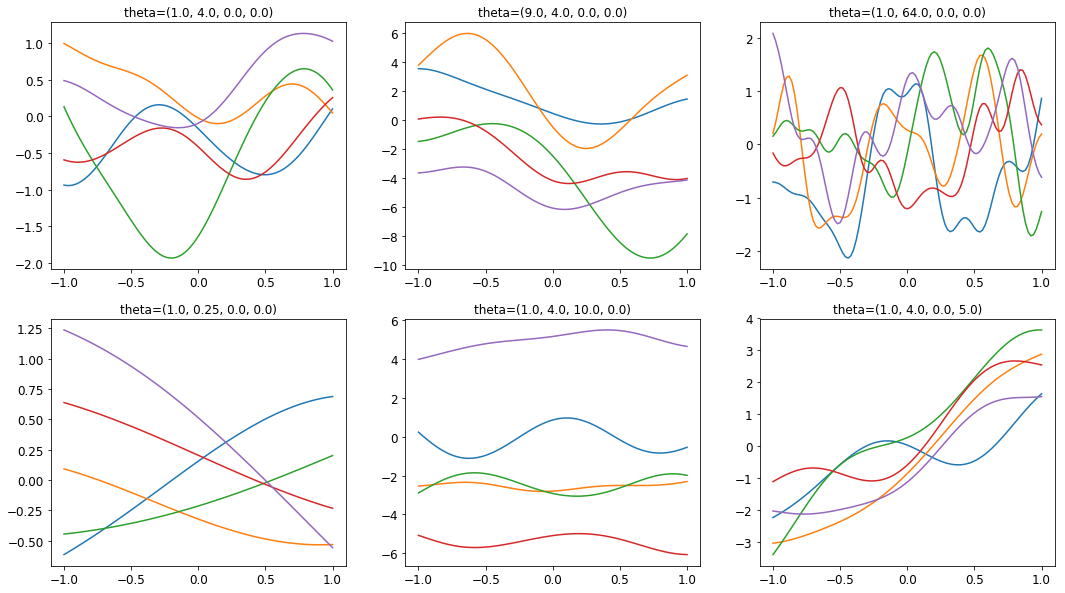
直感的にも分かるように、$\theta_0$は振幅を、$\theta_1$は長さスケールを決めていることが見て取れます11。
3.2 データ
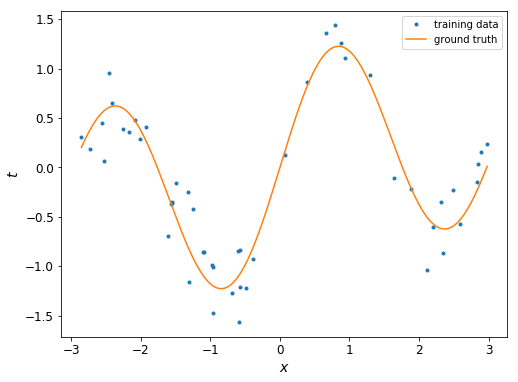
では、いよいよ回帰を行っていきましょう。使うのは、次のトイデータです。
$$
\begin{align}
t &= f(x) + \varepsilon \
f(x) &= \sin(2x) + 0.2 \sin x + 0.1x \
\varepsilon &\sim \mathcal{N}(0.0, 0.09)
\end{align}
$$
データ点の個数は50です。
3.3 回帰(ハイパーパラメーター固定)
まず、ハイパーパラメーターを固定してガウス過程回帰を行ってみましょう。
Thts = np.array([[1.0, 4.0, 0.0, 0.0],
[9.0, 4.0, 0.0, 0.0],
[1.0, 64.0, 0.0,0.0],
[1.0,0.25, 0.0, 0.0],
[1.0, 4.0, 10.0, 0.0],
[1.0, 4.0, 0.0, 5.0]
])
beta = 3.0
kernel = MyKernel(theta = np.array([0.0, 0.0, 0.0, 0.0]), bounds=[[0.0, None],[0.0, None],[0.0, None],[0.0, None]])
gpr = GPRegression(kernel=kernel, beta=beta)
fig = plt.figure(figsize=(18,10))
cnt = 0
while cnt < len(Thts):
theta = Thts[cnt]
kernel.theta = theta
gpr.fit(X, t)
mean, std = gpr.predict(Xtest, return_std=True)
ax = fig.add_subplot(2, 3, cnt+1)
plot_result(mean, std, ax)
ax.set_title(f"beta={gpr.beta}, theta = ({theta[0]}, {theta[1]}, {theta[2]}, {theta[3]}) \n log_likelihod : {-cost_and_grad(beta=gpr.beta, theta=gpr.kernel.theta, kernel=gpr.kernel, X=X, t=t, return_grad=False)}")
cnt += 1
plt.show()
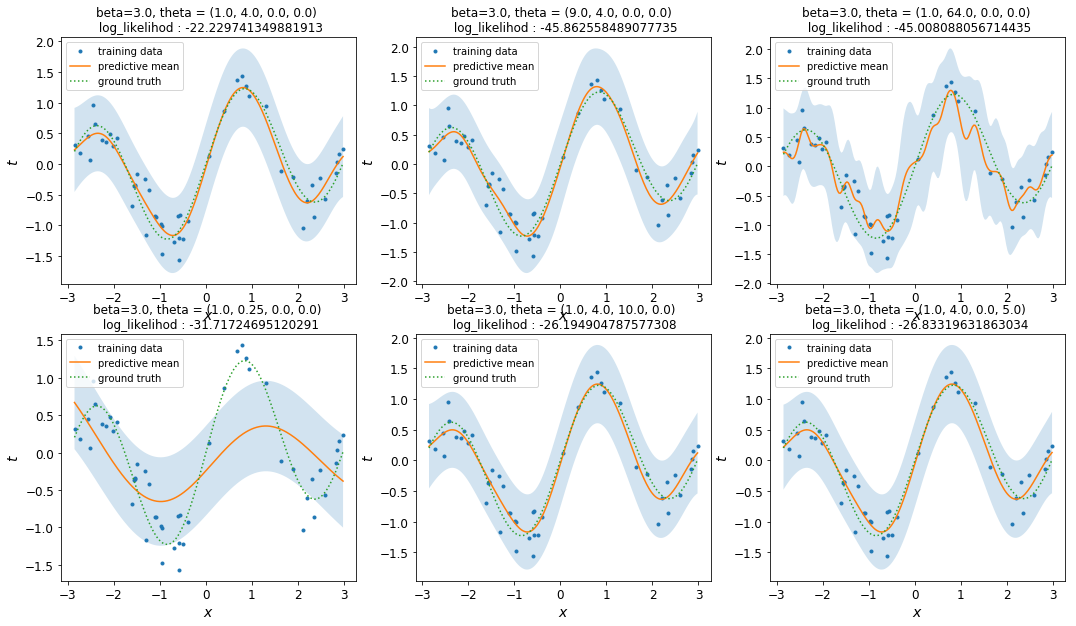
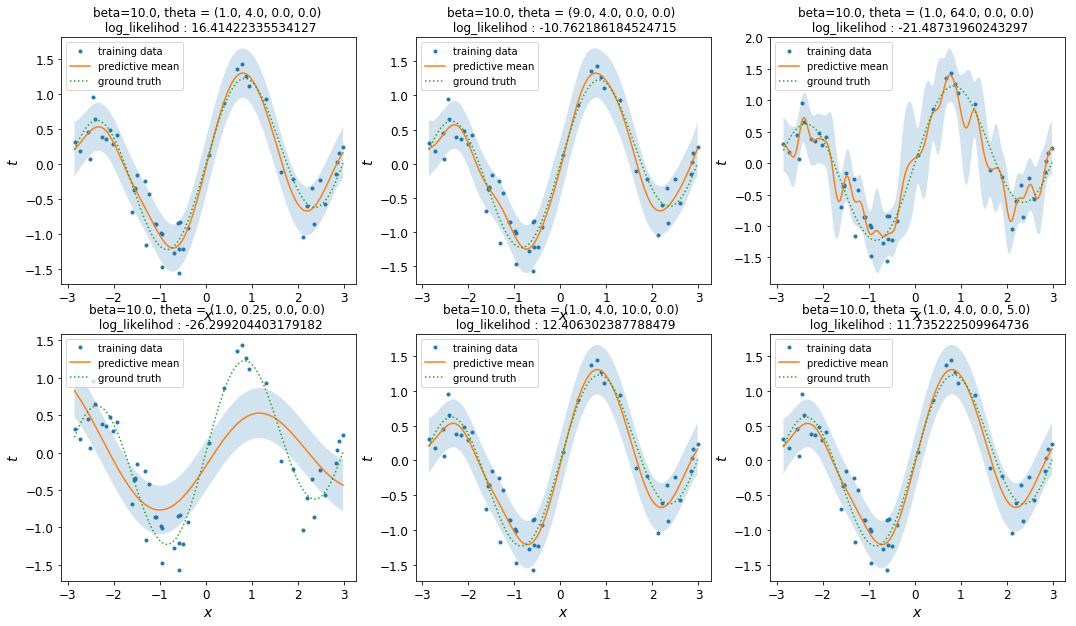
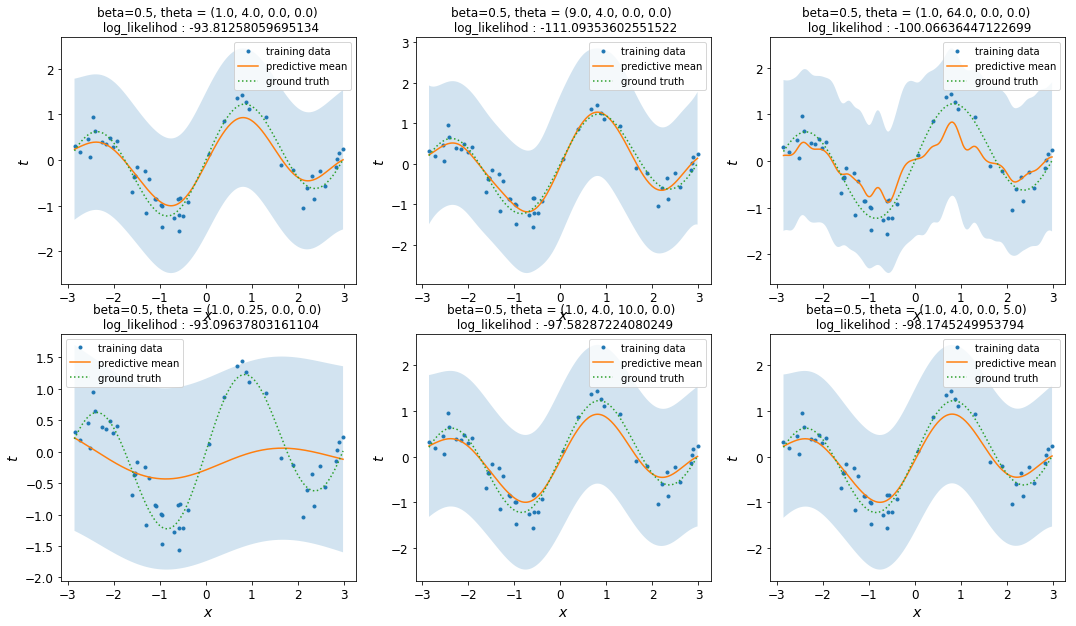
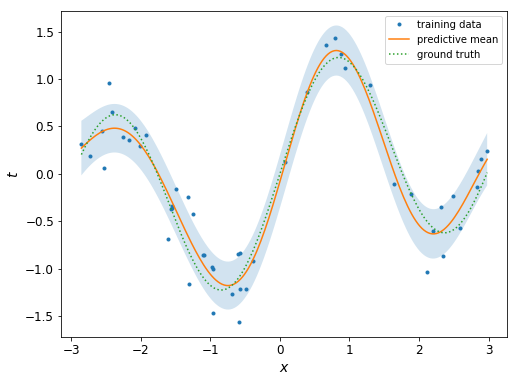
先ほどの節のハイパーパラメーターの組を用いて回帰を行った結果が以下の図です。$\beta=3.0$としてあります。
- 実線が予測平均、水色で彩色された領域が予測平均$\pm$予測標準偏差を表します。
- 点線が真の函数、点が訓練データを表します。
-
log_likelihoodとして書かれている数字は、対数周辺尤度の値を指します。
$\theta_1$の値が結果に大きな影響を与えていることが見て取れます。具体的には、$\theta_1$が大きい(長さスケールが小さい)と予測平均は細かく振動し、$\theta_1$が小さい(長さスケールが大きい)と予測平均はのっぺりしたものになります。これは直感的にも納得いく結果ですね。
対して、$\theta_0, \theta_2, \theta_3$が結果にどう影響しているかは、なんとも言いがたいというのが正直なところです。
また、$\beta$を大きくすると全体的に水色の領域が小さくなり、$\beta$を小さくすると水色の領域が大きくなります。これは、$\beta$の逆数がノイズの強さを表すことから納得できるかと思います。
3.4 ハイパーパラメーター最適化
先ほどは、ハイパーパラメーターを帰るとガウス過程回帰の結果が大幅に変わることを見てきました。この節では、それらのハイパーパラメーターを、「周辺尤度を最大化する」という基準で決めます。
kernel = MyKernel(theta = np.array([2.0, 1.0, 0.01, 0.02]), bounds=[[0.0, None],[0.0, None],[0.0, None],[0.0, None]])
gpr = GPRegression(kernel=kernel, beta=1.0)
gpr.fit(X, t, optimize_hparams=True)
mean, std = gpr.predict(Xtest, return_std=True)
print(f"beta = {gpr.beta}")
print(f"theta={kernel.theta}")
print(f"log_likelihod : {-cost_and_grad(beta=gpr.beta, theta=gpr.kernel.theta, kernel=gpr.kernel, X=X, t=t, return_grad=False)}")
plot_result(mean, std)
結果はこちら
beta = 17.201507415481835
theta=[0.55294478 1.6059704 0. 0. ]
log_likelihod : 40.25398887950302
さきほどより綺麗な結果になってますね! 具体的には:予測平均は真の値に近く、周辺尤度もさきほどの例(適当なハイパーパラメーターで計算したもの)に比べて大きくなっていることが分かります。
4 まとめ
この記事では、PRML第6章のガウス過程回帰を実装しました。
具体的には、カーネル函数を表すクラスMyKernelと、ガウス過程回帰を行うクラスGPRegressionを実装しました。後者には、周辺尤度最大化を基準に、ハイパーパラメーターを自動で選ぶ機能も持たせました。
また、トイデータを使って、ハイパーパラメーターの値を変えると回帰の結果がどのように変化するかを観察しました。ついで、周辺尤度最大化を用いることによって、より適切なハイパーパラメーターを自動で決めることができることを見ました。
PRML3章では特徴量の次元(基底関数の本数)$M$を、入力の次元$d$に対して指数的に大きくする必要がありましたが、ガウス過程回帰ではこのような問題は起きません。実際、カーネル函数の形によっては、$M= \infty$を扱うことができるのは、ガウス過程回帰の利点の1つと言えるでしょう。
一方、ガウス過程回帰では$C^{-1}$を計算するために$\mathcal{O}(N^3)$の計算量が必要になります。そのため、データ数が大きくなるとガウス過程回帰を直接適用するのは困難になります。
この問題に対処するために様々な近似手法が提案されているとのことです。機会があれば、これらの手法についても調査/理解/実装をしてみたいと考えています。
-
PRMLの内容をなぞるだけになってしまうので、この記事ではほぼ全て省略します。 ↩
-
この記事で与えるガウス過程の定義は、数学的には全く厳密ではありません。数学的に厳密な取り扱いについては、こちらのマスタケさんの記事が参考になるかと思います。 ↩
-
そもそもそんな確率過程が存在するのか、といった話については私はきちんとは理解できていません。気になる方は上記の記事をご覧いただければと思います。 ↩
-
上では$y$を函数の意味で用いていたので、これはabuse of notationですね。。。この後、函数としての$y$は登場しないので、文脈で区別はつくかと思います。 ↩
-
正確には、ここでノイズがi.i.d.という仮定を課しています。 ↩
-
この記事では一種類のカーネル函数しか用いませんが、同じ振る舞いをするクラスを自分で書けば、いろいろなカーネル函数を付け替えることができます。 ↩
-
カーネル行列全体を求めるためには$\mathcal{O}(N^2)$かかりますが、対角成分だけなら$\mathcal{O}(N)$で済みます。 ↩
-
加えて、$K$が正定値であるためには、$\theta_0, \theta_2, \theta_3$のうち少なくとも1つが正である必要があります。 ↩
-
ここで、$\tau_0, \dots, \tau_{N_{test}-1}$の同時分布については何も言ってないことに注意。 ↩
-
ここではデータ点ではなく、ガウス過程によって得られる1つの函数が1つのサンプルとなります。 ↩
-
残りのパラメーターの直感的な意味については、自信がありません。。。 ↩