LoginSignup
4
3

More than 5 years have passed since last update.

@amber_kshz

PRML第4章のロジスティック回帰をPythonで実装

Last updated at Posted at 2018-09-29

2018/10/6追記 : この記事の内容に対応するJupyter notebookを更新しました( https://github.com/amber-kshz/PRML )。Qiitaで対応する記事も書く予定です。

この記事では、PRML第4章で述べられている、(多クラス)ロジスティック回帰を実装します。

対応するjupyter notebookは筆者のgithubリポジトリ( https://github.com/amber-kshz/PRML/blob/a98c769229b75515fefa6fe0d7d01817493f1b5a/notebooks/LogisticClassification.ipynb )にあります。連載の方針や、PRMLの他のアルゴリズムについては、まとめページ( https://qiita.com/amber_kshz/items/e912a59ffc1365cb6adf )をご覧ください。

前回と同様、PRMLの本に載っている理論のおさらいをし、数式をコードに翻訳して、最後に実際に動かした結果を見ることにします。

1 理論のおさらい

まず、PRMLの4章(正確には4.3.4節)に書かれていることのおさらいです。すこーしだけ本と記号の定義が異なります1が、それ以外は同じなので、内容を知っている方は軽く読み飛ばしていただいて大丈夫です。

1.1 設定

  • $N \in \mathbb{N}$を訓練データの個数、
  • $d \in \mathbb{N}$を入力(特徴量)の次元、
  • $\mathcal{C} = \left\{ 0, 1, \dots, C-1 \right\}$をクラスラベルの集合、
  • $x_0, x_1, \dots , x_{N-1} \in \mathbb{R}^d$を訓練データの入力(特徴量)、$y_0, y_1, \dots, y_{N-1} \in \mathcal{C}$を訓練データのラベル、$y := {}^t (y_0, \dots, y_{N-1}) \in \mathcal{C}^N$、
  • $t_n \in \left\{ 0,1\right\}^{C}$ を$y_n$の1-of-$C$符号化、($y_n = c$なる$n$に対して、$t_n$は第$c$成分だけが1で他は0のベクトルとします。

1.2 モデル

多クラスロジスティック回帰では、次のモデルを仮定します(PRMLの(4.104)式参照。)。
$$
\begin{align}
p(y|x,\theta) = \frac{\exp\left[{\theta^{(y)}}^T \phi(x)\right] }{ \sum_{y'=0}^{C-1} \exp\left[{\theta^{(y')}}^T \phi(x)\right] }
\end{align}
$$
ただし、

  • $\phi : \mathbb{R}^d \rightarrow \mathbb{R}^M $, $\phi(x) = (\phi_0(x), \dots, \phi_{M-1}(x))^T$は基底関数、$M$は基底関数の本数、
  • $\theta^{(y)} \in \mathbb{R}^M$は重みを表すパラメーター(学習時にはこのパラメーターを調整します。)、
  • $\theta = \left( {\theta^{(0)}}^T, \dots, {\theta^{(C-1)}}^T \right)^T \in \mathbb{R}^{CM}$　です。

後の実装の際には、以下の"線型"基底関数を用います：
$$
\begin{align}
\phi_j(x) = \begin{cases}
1 & (j=0)\\
x^{(j-1)} & (j = 1.\dots, d)
\end{cases}
\end{align}
$$
ただし、$x^{(j)}$は$x \in \mathbb{R}^d$の第$j$成分を表します。

また、$\Phi$を以下で定められる$N \times M$行列とします:
$$
\begin{align}
\Phi = (\Phi_{i,j}), \ \ \Phi_{i,j} = \phi_j(x_i)
\end{align}
$$

1.3 学習

1.3.1 損失函数

ロジスティック回帰の学習では、次の損失函数を最小化するような$\theta$を選びます(PRMLの(4.107), (4.108)参照。)。第1項は尤度の対数に$-1$をかけたもの、第2項は$l^2$正則化項です。
$$
\begin{align}
J(\theta) := - \frac{1}{N} \sum_{n=0}^{N-1} \sum_{c=0}^{C-1} t_{n,c} \log p_{n,c} + \frac{\lambda}{2N} | \theta |^2,
\end{align}
$$
ただし、
$$
\begin{align}
p_{n,c} &:= p(c|x_n,\theta) \\
t_{n,c} &:= \delta_{y_n, c}
\end{align}
$$
です。

1.3.2 勾配

最小化を行うためには、損失函数の$\theta$に関する微分(勾配)が必要になります。
上記の損失函数を$\theta^{(c)}_{j}$で微分することにより、次の勾配が得られます(PRMLの(4.109)参照。)。
$$
\begin{align}
\frac{\partial J}{\partial \theta^{(c)}_{j}} = \frac{1}{N} \sum_{n=0}^{N-1} ( p_{n,c} - t_{n,c}) \phi_j(x_n) +\frac{\lambda}{N} \theta^{(c)}_{j}
\end{align}
$$

2 数式からコードへ

では、ここまでの数式をコードに翻訳していきましょう。

  • まず、ここまで出てきた変数を行列(2-D array)で表すための函数を書きます。
  • Logistic回帰分類器を書きます。損失函数や勾配もこの中に含めておきます。

2.1 行列表記

まず、ここまで出てきた$p$や$t$などの2つの添え字を伴う変数を行列(正確には2-D numpy array)で表しておきます。こうしておくと、後の計算が行列の積などで書け、いろいろと便利になります。
具体的には、arrayを以下のように定義します。

  • Phi : (N, M) array, Phi[n, m] := $\phi_m(x_n)$
  • Theta : (C, M) array, Theta[c, j] := $\theta^{(c)}_{j}$
  • T : (N,C) array,　T[n, c] := $t_{n, c}$
  • P : (N, C) array, P[n, c] := $p_{n, c}$

それぞれのarrayを生成する函数を定義しておきましょう。

まず、Phiから。これは(今の設定では)1を含む列を加えるだけなので容易です。


def genPhimat(X):
    '''
    This function generates the design matrix Phi from X, the input data

    Parameters
    ----------
    X : 2-D numpy array
        (N,d) numpy array, with X[n, i] = i-th element of x_n

    Returns
    ----------
    Phi : 2-D numpy array
        The design matrix
    '''
    N = len(X)
    if len(np.shape(X)) == 1:
        d = 1
    else:
        d = np.shape(X)[1]
    Phi = np.zeros((N,d+1))
    Phi[:,0] = np.ones(N)
    Phi[:,1:] = np.reshape(X, (N,d))
    return Phi

次に、Tを生成する函数。「bool型をfloat型のarrayに代入するとTrueが1に、Falseが0に変換される」ことを利用します。


def genTmat(y, C):
    '''
    This function generates the matrix T from the training label y and the number of classes C

    Parameters
    ----------
    y : 1-D numpy array
        The elements of y should be integers in [0, C-1]
    C : int
        The number of classes

    Returns
    ----------
    T : (len(y), C) numpy array
        T[n, c] = 1 if y[n] == c else 0
    '''
    N = len(y)
    T = np.zeros((N, C))
    for c in range(C):
        T[:, c] = (y == c)
    return T

最後に、Pです。
Pを$P$、Phiを$\Phi$、Thetaを$\Theta$と行列で表すと、
$$
\begin{align}
P_{n,c} &= \frac{\exp\left[\sum_{j=0}^{M-1} \theta^{(c)}_{j} \phi_{j}(x_n)\right] }{ \sum_{c'=0}^{C-1} \exp\left[ \sum_{j=0}^{M-1} \theta^{(c')}_{j} \phi_{j}(x_n) \right]} \\
&= \frac{ \exp \left[ \left( \Phi \Theta^T \right)_{n, c'} \right] }{ \sum_{c'=0}^{C-1} \exp\left[ \left( \Phi \Theta^T \right)_{n, c'} \right] }
\end{align}
$$
となります。このように行列の積を利用すると、対応するコードは以下のように書けます。


def genPmat(Theta, Phi):
    '''
    This function generates the matrix P from the weight Theta and the design matrix Phi

    Parameters
    ----------
    Theta : 2-D numpy array
        Matrix representing the weight parameter
    Phi : 2-D numpy array
        The design matrix

    Returns
    ----------
    P : 2-D numpy array
    '''
    P = np.exp( Phi @ (Theta.T) )
    P = P/np.reshape( np.sum(P, axis= 1), (len(Phi),1)  ) 
    return P

2.2 ロジスティック回帰分類器

次に、ロジスティック回帰を行うためのクラスLogisticClfを作ります。
次の属性を持たせることにします:

  • 分類するラベルの種類の個数$C$ (self.C)
  • 正則化パラメーター$\lambda$ (self.lam)

また、次のメソッドを持たせます。

  • コンストラクタ (__init__)
  • 損失函数と勾配(JandGradJ)。ただし、scipy.optimize.minimizeの仕様上、入力となる重みパラメーターと、出力の片方の勾配は、ベクトル(1-D array)で扱うことにします。
  • 学習を行うメソッド(fit)
  • 入力に対して、各ラベルの確率を返すメソッド(predict_proba)
  • 入力に対して、予測されるラベルを返すメソッド(predict)

2.2.1 損失函数と勾配

上記の行列表記を用いると、
$$
\begin{align}
J(\Theta)
&= - \frac{1}{N} \sum_{n=0}^{N-1} \sum_{c=0}^{C-1} t_{n,c} \log p_{n,c} + \frac{\lambda}{2N} | \theta |^2 \\
&= -\frac{1}{N} sum(T \ast \log P) + \frac{\lambda}{2N} | \Theta |_{2}^{2}
\end{align}
$$
となります。ただし、$\ast$は行列の要素ごとの積、$\log$は行列の要素ごとに対数をとることを表し、$sum$は行列の全要素の和を取ることを表します。

また、$\frac{\partial J(\Theta)}{\partial \Theta}$を(C,M)行列とみなすと、
$$
\begin{align}
\frac{\partial J(\Theta)}{\partial \Theta}
&= \left( \frac{1}{N} \sum_{n=0}^{N-1} ( p_{n,c} - t_{n,c}) \phi_j(x_n) + \frac{\lambda}{N} \theta^{(c)}_{j} \right)_{c,j} \\
&= \frac{1}{N} (P-T)^T \Phi + \frac{\lambda}{N} \Theta
\end{align}
$$
と書けます。対応するメソッドは以下の通りとなります：


    def JandGradJ(self, thtvec, Phi, T):
        '''
        This method calculate the loss function and its gradient

        Parameters
        ----------
        thtvec : 1-D numpy array 
            (M*C,) array, which represents the weight parameter Theta, in flattened form
        Phi : 2-D numpy array
            (N, M) array, design matrix
        T : 2-D numpy array
            (N, C) array, where T[n, c] = 1 if y[n] == c else 0

        Returns
        ----------
        J : float
            The value of loss function
        gradJvec : 1-D numpy array
            The gradient of the loss function with respect to the weight parameter Theta, in flattened form

        '''
        N, M = np.shape(Phi)
        Theta = np.reshape(thtvec, (self.C, M))
        P = genPmat(Theta, Phi)
        J = -1.0/N*np.sum(T*np.log(P)) + self.lam/(2.0*N)*np.linalg.norm(thtvec)**2
        gradJmat = 1.0/N*((P - T).T) @ Phi + self.lam/N*Theta
        gradJvec = np.reshape(gradJmat, len(thtvec))
        return J, gradJvec

2.2.3 fitメソッド

さきほどの損失函数と勾配を用いて、fittingを行います。

損失函数の最小化には、やや手抜きですが、scipy.optimize.minimizeを用いることにします(あらかじめminimizeとしてimportしておきます。)。

また、minimizeのためのx0(変数の初期値)は、ここでは全てが1の配列にしておきます(凸最適化なので、初期値はあまり気にする必要はないかと思います。)


    def fit(self, X, y):
        '''
        Parameters
        ----------
        X : 1-D or 2-D numpy array
            (N,) or (N, d) array, representing the training input data
        y : 1-D numpy arra
            (N,) array, representing training labels
        '''
        Phi = genPhimat(X)
        T = genTmat(y, self.C)
        N, M = np.shape(Phi)

        tht0 = np.ones(M*self.C)
        result = minimize(lambda x : self.JandGradJ(x, Phi, T), x0=tht0, jac=True)
        self.Theta = np.reshape(result['x'], (self.C, M))

2.2.2 LogisticClf全体のコード

これに他のメソッド(__init__やpredictなど)を付け加えると、以下の通りです。


from scipy.optimize import minimize

class LogisticClf:
    def __init__(self, C, lam):
        self.C = C  # the number of labels
        self.lam = lam #regularization parameter
        self.Theta = None

    def JandGradJ(self, thtvec, Phi, T):
        '''
        This method calculate the loss function and its gradient

        Parameters
        ----------
        thtvec : 1-D numpy array 
            (M*C,) array, which represents the weight parameter Theta, in flattened form
        Phi : 2-D numpy array
            (N, M) array, design matrix
        T : 2-D numpy array
            (N, C) array, where T[n, c] = 1 if y[n] == c else 0

        Returns
        ----------
        J : float
            The value of loss function
        gradJvec : 1-D numpy array
            The gradient of the loss function with respect to the weight parameter Theta, in flattened form

        '''
        N, M = np.shape(Phi)
        Theta = np.reshape(thtvec, (self.C, M))
        P = genPmat(Theta, Phi)
        J = -1.0/N*np.sum(T*np.log(P)) + self.lam/(2.0*N)*np.linalg.norm(thtvec)**2
        gradJmat = 1.0/N*((P - T).T) @ Phi + self.lam/N*Theta
        gradJvec = np.reshape(gradJmat, len(thtvec))
        return J, gradJvec

    def fit(self, X, y):
        '''
        Parameters
        ----------
        X : 1-D or 2-D numpy array
            (N,) or (N, d) array, representing the training input data
        y : 1-D numpy arra
            (N,) array, representing training labels
        '''
        Phi = genPhimat(X)
        T = genTmat(y, self.C)
        N, M = np.shape(Phi)

        tht0 = np.ones(M*self.C)
        result = minimize(lambda x : self.JandGradJ(x, Phi, T), x0=tht0, jac=True)
        self.Theta = np.reshape(result['x'], (self.C, M))

    def predict_proba(self, X):
        '''
        Parameters
        ----------
        X : 1-D or 2-D numpy array
            (N,) or (N, d) array, representing the training input data
        Returns
        ----------
        proba : 2-D numpy arra
            (len(X), self.C) array, where proba[n, c] represents the probability that the n-th instance belongs to c-th class
        '''
        return genPmat(self.Theta, genPhimat(X))

    def predict(self, X):
        '''
        Parameters
        ----------
        X : 1-D or 2-D numpy array
            (N,) or (N, d) array, representing the training input data
        Returns
        ----------
        classes : 1-D numpy arra
            (len(X), ) array, where classes[n] represents the predicted class to which the n-th instance belongs
        '''
        tmp = self.predict_proba(X)
        return np.argmax(tmp, axis=1 )

3 実験

ということで、いよいよ実験です。
今回は簡単な2次元のデータと、MNISTの手書き文字データを用います。

3.1 Toy data

まずは、簡単な2次元のデータを用います。


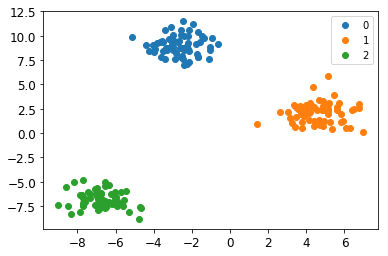
X, y = datasets.make_blobs(n_samples=200, n_features=2, centers=3)

image.png

このデータで先ほどのLogisticClfを学習させ、予測結果をプロットしたのが以下の図です(カラーバーの数字の0, 1, 2が予測されたラベルを表します。)。
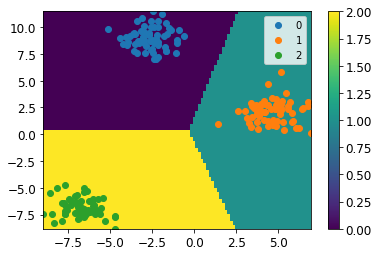
image.png
綺麗に分類できているのが見て取れるかと思います。なお、この図では決定境界が直線になっていますが、これは我々が基底関数$\phi$として、"線型"なものを用いたことに由来します。非線形な基底函数を用いた場合、一般に境界は直線になるとは限りません。

3.2 手書き文字データ

さて、ここまででひとまずコードが意図したとおりに動いているようだということは分かりました。
ただ、データが単純すぎるので、もうちょっと複雑なデータでも試してみましょう。ここでは、MNISTの手書き文字データを用います。


digits = datasets.load_digits()
dat_train, dat_test, label_train, label_test = train_test_split(digits.data, digits.target, test_size=0.25)

せっかくなので、正則化パラメーター$\lambda$の値も変えて試してみましょう。結果は以下の通りでした。

lambda = 0.1
train accuracy score: 1.0
test accuracy score: 0.9533333333333334

lambda = 1.0
train accuracy score: 1.0
test accuracy score: 0.9577777777777777

lambda = 10.0
train accuracy score: 0.9992576095025983
test accuracy score: 0.9666666666666667

だいたい正しく分類できていることに加え、$\lambda$が大きくなるにつれて汎化誤差が下がっていることも見て取れます。正則化パラメーターを大きくすることは、biasを上げる代わりにvarianceを下げることに対応するので、この振る舞いは直感的にも納得のいくものかと思います。

4 まとめ

今回は、分類問題に対するロジスティック回帰を実装しました。また、数値実験を通じて、正則化パラメーターが結果に与える影響についても観察しました。

ただ、この実装は実行速度に難があります2。今回は数式を安直にコードに翻訳して実装することに主眼を置いたため実行速度は真面目に考えませんでしたが、実際に使えるものを書こうとする場合は、きちんと頭を使って実装する必要があるかと思います3。

  1. 本の$K$を$C$、$k$を$c$、$y_{n,k}$を$p_{n,c}$, $w_k$を$\theta^{(c)}$と表しています。 ↩

  2. きちんと測ってはいませんが、上述のMNISTのデータを一回学習するのに数秒-10秒程度かかりました。対して、scikit-learnのLogisticRegressionを用いた際は1秒程度で終了しました。 ↩

  3. 恐らく、最適化で用いたminimizeの具体的なアルゴリズム選択をさぼったせいかと思います。Hessianの情報を与えてこれを活用すれば反復の回数が減ると思うので、おいおいやってみたいと思います。 ↩

4
3
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
4
3