この記事は個人的なお勉強用のメモです。
講義
主成分分析とは
- 教師なし学習
- 変量(特徴量)の個数を減らす=次元を減らす。
- 次元を減らす際はなるべく情報量を落とさない。
- 2次元・3次元まで落とすと可視化できる。
求め方
- すべてのデータで成分ごとに平均をとる(1つの平均的なベクトルを作る)
- すべてのデータで平均との差をとる。(成分が差になっている行列を作る。)
- この行列の分散を求める。(分散共分散行列)
- 線形変換後のベクトルを求める。
分散共分散行列
分散共分散行列とは、データごとに共分散を求め、それを行列にしたもの。
対称行列。
対角成分は同じデータ同士の共分散なので、単なる分散になる。
実装上のキーワード
- 共分散行列の作成 np.cov
- 固有値分解 np.linalg.eig
戻り値はタプル、1つ目は固有値、2つ目は固有ベクトル - ソートしてインデックスを取得 np.argsort
引数に -1 を指定すると降順になる。
この関数はあくまでもソート後のインデックスを返すのみ。
用語
- 次元の呪い
Bellman「空間の次元が増えるのに対応して、問題の複雑さが指数関数的に大きくなる」 - 球面集中現象
高次元空間の場合、データが超球面上に分布しやすくなる。
高次元になると、点がほとんど同じ距離になる。 - 特徴選択
特徴量の組み合わせを最適化する。 - 寄与率
ある固有値が全体のどの程度の割合で情報を含むか。
寄与率が高い固有値を成分として採用する(削減せずに残す)。
実装演習
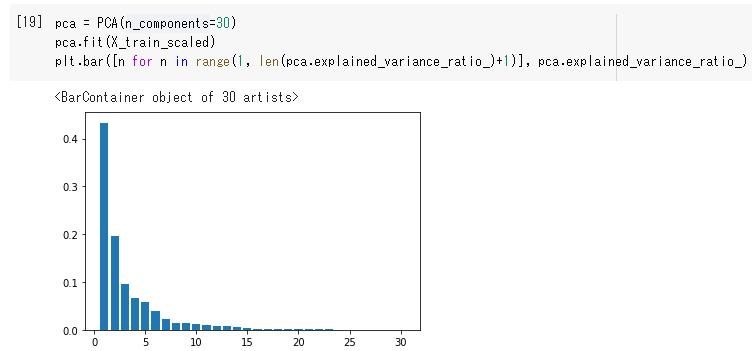
pca.explained_variance_ratio_変数に、成分ごとの割合が降順で格納される。
それを棒グラフに表示している。
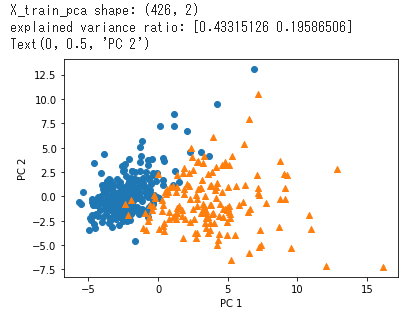
第1成分が45%くらい、第2成分が20%くらいなので、この2つの成分だけでも65%くらいの
情報を表現できているという意味。
いくつかの他方の領域に含まれており、正しく分類できていない個所が多く存在する。
元は97%だったのでそれに比べると累積の寄与率が65%程度では正解率がかなり落ちる。
修了テスト~練習問題~
問題76(主成分分析)
Wikipediaより
主成分分析は、相関のある多数の変数から相関のない少数で全体のばらつきを
最もよく表す主成分と呼ばれる変数を合成する多変量解析の一手法。
変量を削除するのではない。
問題77(主成分分析)
主成分分析の計算の過程で分散を計算する。
分散がもっとも大きい成分を求めるため。
問題78(主成分分析)
a_1=
\begin{pmatrix}
a_{1x}\\
a_{1y}
\end{pmatrix}
,
a_2=
\begin{pmatrix}
a_{2x}\\
a_{2y}
\end{pmatrix}
,
a_3=
\begin{pmatrix}
a_{3x}\\
a_{3y}
\end{pmatrix}\\
e=
\begin{pmatrix}
e_{x}\\
e_{y}
\end{pmatrix}\\
分散 V=
\frac{(a_1e)^2+(a_2e)^2+(a_3e)^2}{3}
式変形すると
分散 V=e^TXe
行列 $X$ を共分散行列という。
演習問題
公式の演習問題が見当たらない。
代わりに某問題集を使って勉強。
def pca(X, n_components):
X = X - X.mean(axis=0)
cov = np.cov(X, rowvar=False)
l, v = np.linalg.eig(cov)
l_index = np.argsort(l)[::-1]
v_ = v[:,l_index]
components = v_[:,:n_components]
T = np.dot(X, components)
return T
- 平均をとる
- 分散共分散行列を求める
- 固有値と固有ベクトルを求める
- 固有値を降順でソートするためのインデックスを求める
- 固有ベクトルを降順でソートする
- n_componentsの個数だけ、固有ベクトルを切り出す
- データを低次元空間に射影する
scikit-learnを使わなくても、Pythonだけでこれほど短いコードで
PCAを実装できる。