正方行列
例1.
\begin{pmatrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{pmatrix}
例2.
\begin{pmatrix}
1 & 2 & 3 & 4 \\
4 & 3 & 2 & 1 \\
4 & -4 & 4 & 4 \\
1 & 1 & 1 & -1 \\
\end{pmatrix}
例3.
\begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn} \\
\end{pmatrix}
零行列
例1.
\begin{pmatrix}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
\end{pmatrix}
例2.
\begin{pmatrix}
0 & 0 & 0 & \cdots & 0 \\
0 & 0 & 0 & \cdots & 0 \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
0 & 0 & 0 & \cdots & 0 \\
\end{pmatrix}
対角行列
例1.
\begin{pmatrix}
1 & 0 & 0 \\
0 & 2 & 0 \\
0 & 0 & 3 \\
\end{pmatrix}
例2.
\begin{pmatrix}
0 & 0 & 0 & 0 & 0 \\
0 & 3 & 0 & 0 & 0 \\
0 & 0 & -2 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & -1 \\
\end{pmatrix}
例3.
\begin{pmatrix}
c_{1} & 0 & 0 & 0 \\
0 & c_{2} & 0 & 0 \\
0 & 0 & \ddots & 0 \\
0 & 0 & 0 & c_{n} \\
\end{pmatrix}
誤っている例1.
{\color{red}{
\begin{pmatrix}
0 & 0 & 1 \\
0 & 2 & 0 \\
3 & 0 & 0 \\
\end{pmatrix}
}}
誤っている例2.
{\color{red}{
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 2 & 0 & 0 \\
0 & 0 & 3 & 0 \\
\end{pmatrix}
}}
三角行列
下三角行列の例1.
\begin{pmatrix}
4 & 0 & 0 \\
2 & 3 & 0 \\
1 & 3 & 4 \\
\end{pmatrix}
下三角行列の例2.
\begin{pmatrix}
a_{11} & 0 & 0 & 0 & 0 \\
a_{21} & a_{22} & 0 & 0 & 0 \\
a_{31} & a_{32} & \ddots & 0 & 0 \\
\vdots & \vdots & \ddots & \ddots & 0 \\
a_{n1} & a_{n2} & \dots & \cdots & a_{nn} \\
\end{pmatrix}
下三角行列の例3.
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 4 & 0 & 0 \\
0 & 3 & 2 & 0 \\
1 & 3 & 0 & 5 \\
\end{pmatrix}
上三角行列の例1.
\begin{pmatrix}
a_{11} & a_{12} & a_{13} & \cdots & a_{1n} \\
0 & a_{22} & a_{23} & \cdots & a_{2n} \\
0 & 0 & \ddots & \ddots & \vdots \\
0 & 0 & 0 & \ddots & \vdots \\
0 & 0 & 0 & 0 & a_{nn} \\
\end{pmatrix}
ハンケル行列
例1.
\begin{pmatrix}
1 & 3 & 4 & 5 \\
3 & 4 & 5 & 7 \\
4 & 5 & 7 & 8 \\
5 & 7 & 8 & 6 \\
\end{pmatrix}
例2.
\begin{pmatrix}
a & b & c & d & e \\
b & c & d & e & h \\
c & d & e & h & g \\
d & e & h & g & h \\
e & h & g & h & i \\
\end{pmatrix}
誤った例1.
\color{red}{
\begin{pmatrix}
e & d & c & b & a \\
f & e & d & c & b \\
g & f & e & d & c \\
h & g & f & e & d \\
i & h & g & f & e \\
\end{pmatrix}
}
転置行列
例1.
A = \begin{pmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9 \\
\end{pmatrix}
→
A^{\mathrm{T}} = \begin{pmatrix}
1 & 4 & 7 \\
2 & 5 & 8 \\
3 & 6 & 9 \\
\end{pmatrix}
例2.
A = \begin{pmatrix}
a & b & c \\
d & e & f \\
\end{pmatrix}
→
A^{\mathrm{T}} = \begin{pmatrix}
a & d \\
b & e \\
c & f \\
\end{pmatrix}
参考画像.
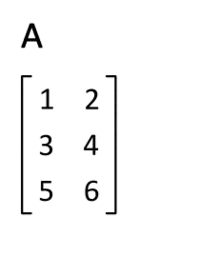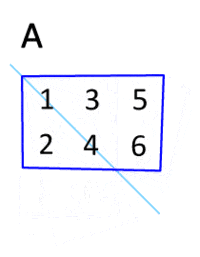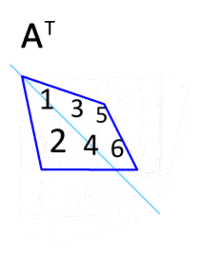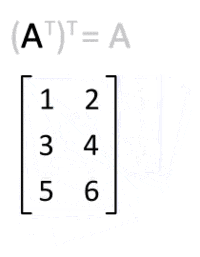 |
|---|
複素共役行列
例1.
A = \begin{pmatrix}
1 & -1 - \mathrm{i} & \\
1 + \mathrm{i} & \mathrm{i} & \\
\end{pmatrix}
→
\overline{A} = \begin{pmatrix}
1 & -1 + \mathrm{i} & \\
1 - \mathrm{i} & -\mathrm{i} & \\
\end{pmatrix}
例2.
A = \begin{pmatrix}
a_{11} + b_{11}\mathrm{i} & a_{12} + b_{12}\mathrm{i} \\
a_{21} + b_{21}\mathrm{i} & a_{22} + b_{22}\mathrm{i} \\
a_{31} + b_{31}\mathrm{i} & a_{32} + b_{32}\mathrm{i} \\
\end{pmatrix}
→
\overline{A} = \begin{pmatrix}
a_{11} - b_{11}\mathrm{i} & a_{12} - b_{12}\mathrm{i} \\
a_{21} - b_{21}\mathrm{i} & a_{22} - b_{22}\mathrm{i} \\
a_{31} - b_{31}\mathrm{i} & a_{32} - b_{32}\mathrm{i} \\
\end{pmatrix}
随伴行列
例1.
A = \begin{pmatrix}
1 & -1 - \mathrm{i} & \\
1 + \mathrm{i} & \mathrm{i} & \\
\end{pmatrix}
→
A^{\dagger} = \overline{A}^{\mathrm{T}} = \begin{pmatrix}
1 & 1 - \mathrm{i} & \\
-1 + \mathrm{i} & -\mathrm{i} & \\
\end{pmatrix}
例2.
A = \begin{pmatrix}
a_{11} + b_{11}\mathrm{i} & \cdots & a_{1n} + b_{1n}\mathrm{i} & \\
a_{21} + b_{21}\mathrm{i} & \cdots & a_{2n} + b_{2n}\mathrm{i} & \\
a_{31} + b_{31}\mathrm{i} & \cdots & a_{3n} + b_{3n}\mathrm{i} & \\
\end{pmatrix}
→
A^{\dagger} = \overline{A}^{\mathrm{T}} = \begin{pmatrix}
a_{11} - b_{11}\mathrm{i} & a_{21} - b_{21}\mathrm{i} & a_{31} - b_{31}\mathrm{i} \\
\vdots & \vdots & \vdots \\
a_{1n} - b_{1n}\mathrm{i} & a_{2n} - b_{2n}\mathrm{i} & a_{3n} - b_{3n}\mathrm{i} \\
\end{pmatrix}
対称行列
例1.
A = A^{\mathrm{T}}
例2.
A = \begin{pmatrix}
1 & 7 & 3 \\
7 & 4 & -5 \\
3 & -5 & 6 \\
\end{pmatrix}
誤った例1.
\color{red}{
\begin{pmatrix}
6 & 7 & 3 \\
7 & 4 & -5 \\
1 & -5 & 6 \\
\end{pmatrix}
}
エルミート行列
例1.
A = A^{\mathrm{\dagger}}
例2.
A = \begin{pmatrix}
3 & -3\mathrm{i} & 1 + \mathrm{i} & 2 - 4\mathrm{i} \\
3\mathrm{i} & -3 & -5 + \mathrm{i} & 4\mathrm{i} \\
1 - \mathrm{i} & -5 - \mathrm{i} & 0 & 1 + \mathrm{i} \\
2 + 4\mathrm{i} & -4\mathrm{i} & 1 - \mathrm{i} & 4 \\
\end{pmatrix}
正規行列
例1.
A^{\mathrm{\dagger}}A = AA^{\mathrm{\dagger}}
例2.
A = \begin{pmatrix}
1 & 2 \\
2 & 1 \\
\end{pmatrix}
例3.
A = \begin{pmatrix}
0 & 2 & 0 \\
0 & 0 & 2 \\
2 & 0 & 0 \\
\end{pmatrix}
単位行列
例1.
\begin{pmatrix}
1 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 \\
0 & 0 & 0 & 0 & 1 \\
\end{pmatrix}
例2.
\begin{pmatrix}
1 & 0 & \cdots & 0 \\
0 & 1 & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & 1 \\
\end{pmatrix}
誤った例1.
\color{red}{
\begin{pmatrix}
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
1 & 0 & 0 & 0 \\
\end{pmatrix}
}
正則行列、逆行列
例1.
AB = I = BA
- $I$は単位行列
- $A$は$B$の正則行列、$B$は$A$の逆行列
- $B$は$A$の正則行列、$A$は$B$の逆行列
例2.
AA^{-1} = I = A^{-1}A
- $A^{-1}$は$A$の逆行列
例3.
A = \begin{pmatrix}
1 & 0 & 0 \\
0 & 2 & 0 \\
0 & 0 & -\frac{1}{5} \\
\end{pmatrix}
B = \begin{pmatrix}
1 & 0 & 0 \\
0 & \frac{1}{2} & 0 \\
0 & 0 & -5 \\
\end{pmatrix}
\\
AB = \begin{pmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{pmatrix}
直交行列
例1.
M^\mathrm{T}M = MM^\mathrm{T} = I
- Iは単位行列
- Mが直行行列
例2.
\begin{pmatrix}
0 & 0 & 1 & 0 \\
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
\end{pmatrix}
例3.
\begin{pmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta \\
\end{pmatrix}
ユニタリ行列
例1.
U^\mathrm{\dagger}U = UU^\mathrm{\dagger} = I
- $I$は単位行列
- $U$がユニタリ行列
例2.
\begin{pmatrix}
\frac{1}{\sqrt{2}} & \frac{i}{\sqrt{2}} \\
\frac{i}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\end{pmatrix}
射影行列
例1.
H = X(X^TX)^{–1}X^T