任意時間の要素列挙可能な部分永続UnionFindの実装例

はじめに

はじめましての人ははじめまして。alumiと申します。
この記事では、一般的な部分永続UnionFindに、「要素列挙」機能を追加した実装について紹介します。
一応前回記事「要素列挙可能Union Findの実装例」の続きなので、そっちを読んでからこっちを読むと理解しやすいかもです。

部分永続UnionFindとは

まず永続データ構造 - Wikipediaを簡単に説明しましょう。ざっくり、

• 部分永続（Partially Persistent）：過去状態の参照のみ可能、最新状態だけ更新が可能
• 完全永続（fully Persistent）：任意の状態の参照・更新が可能

という感じです。

今回扱う部分永続UnionFindは、通常のUnionFindの機能に加えて、以下の追加機能を提供します。

• uniteごとに時間$t$が進む
• ある時間$t$において、要素$x,y$が同じ集合に属するかを判定できる
• ある時間$t$において、要素$x$が含まれる集合の要素数を求めることができる
• 要素$x,y$がいつ併合されたかを求めることができる

普通のUnionFindに時間の概念が追加されたような感じですね。
これらの機能により、UnionFindの履歴を保持しつつ、過去の状態を効率的に参照できるようになります。

本記事ではまずこれらの機能を有する部分永続UnionFind（以下「一般的な部分永続UnionFind」と呼びます）の実装を紹介した後に、本題の要素列挙可能な部分永続UnionFindの実装を紹介します。
一般的な実装に関する説明は以下の参考記事と多分に重複しているので、わかりにくかったら参考記事をご参照ください。

• 参考記事
  • pythonで永続UnionFind実装 - Qiita
  • やぶについて書きます
  • Partial Persistent Union Find My Algorithm : kopricky アルゴリズムライブラリ

一般的な実装は知ってる・持ってるという人は「要素列挙機能の追加」までジャンプしてくださいな。

実装

class PartiallyPersistentDisjointSet:
    INF = 1 << 60

    def __init__(self, N: int) -> None:
        self.cur_time = 0
        self.par = [-1] * N
        self.merge_times = [self.INF] * N
        self.size_history = [[(0, 1)] for _ in range(N)]

    def _find_root(self, t: int, x: int) -> int:
        while self.merge_times[x] <= t:
            x = self.par[x]
        return x

    def unite(self, x: int, y: int) -> bool:
        rx = self._find_root(self.cur_time, x)
        ry = self._find_root(self.cur_time, y)
        self.cur_time += 1
        if rx == ry:
            return False
        if self.par[rx] > self.par[ry]:
            rx, ry = ry, rx
        self.par[rx] += self.par[ry]
        self.par[ry] = rx
        self.merge_times[ry] = self.cur_time
        self.size_history[rx].append((self.cur_time, -self.par[rx]))
        return True

    def is_same(self, t: int, x: int, y: int) -> bool:
        return self._find_root(t, x) == self._find_root(t, y)

    @staticmethod
    def _binary_search(ok, ng, is_valid):
        while abs(ok - ng) > 1:
            mid = (ok + ng) >> 1
            if is_valid(mid):
                ok = mid
            else:
                ng = mid
        return ok

    def get_size(self, t: int, x: int) -> int:
        rx = self._find_root(t, x)
        is_valid = lambda x: self.size_history[rx][x][0] <= t
        idx = self._binary_search(0, len(self.size_history[rx]), is_valid)
        return self.size_history[rx][idx][1]

    def get_merge_time(self, x: int, y: int) -> int:
        if not self.is_same(self.cur_time, x, y):
            return -1
        is_valid = lambda t: self.is_same(t, x, y)
        return self._binary_search(self.cur_time, -1, is_valid)

インスタンス変数

• cur_time = 0
  • 最新時間を管理する変数
• par = [-1] * N
  • 要素の関係を木として見たときの、各要素の親に当たる要素を管理する配列
  • 親自身は自分が担当する集合の要素数を負で持つ
• merge_times = [self.INF] * N
  • 併合された時間を管理する配列
  • ある集合$Y$が、併合によって別の集合$X$の子になるとき、$Y$の根をryとしてmerge_times[ry]に併合された時刻を記録する（後述）
• size_history = [[(0, 1)] for _ in range(N)]
  • 併合ごとの要素数を管理する配列
  • 親側に、併合が行われた時刻とその時の要素数がtupleで保存されている
  • 空間：$O(N+M)$

メソッド

• $N$：集合の要素数
• $M$：操作回数
• _find_root(t: int, x: int) -> int:
  • 任意時刻tにおけるxの根を探す
  • 時間：$O(\log{N})$
• unite(x: int, y: int) -> bool:
  • 最新時刻においてx, yそれぞれが属する集合を併合
  • 時間：$O(\log{N})$
    • _find_rootがボトルネック
• is_same(t: int, x: int, y: int) -> bool:
  • 時刻tにおいてx, yが同じ集合に属するか判定する
  • 時間：$O(\log{N})$
• _binary_search(ok, ng, is_valid):
  • 内部メソッド。二分探索を行う
  • 時間：$O(\alpha \log{|ok-ng|})$
    • $O(\alpha)$はis_validの評価にかかる時間
• get_size(t: int, x: int) -> int:
  • 時刻tにおいてxが属する集合の要素数を返す
  • 時間：$O(\log{N}+\log{M})$
• get_merge_time(x: int, y: int) -> int:
  • x, yが併合された時刻tを返す
  • 時間：$O(\log{N}*\log{M})$

実装の詳細

各メソッドの実装詳細について、コードと共に解説していきます。

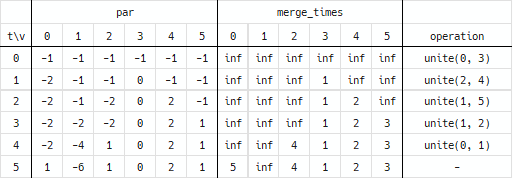
操作時の配列の遷移

• parは各時間において普通のUnionFindと同じように振る舞う
  • 要素が負の場合はその集合の根を意味し、絶対値がその集合の要素数を表す
• merge_timesは自分が親の状態から誰かの子になった時間を記録する
  • 最後まで親である要素はずっとinfとなる（根であり続けた1が典型例）
• 最終的にデータとして持つのは最新の状態（一番下）のみ。なのでメモリは余裕（$O(N)$）

_find_rootの仕組み

merge_timesには、各要素が誰かの子になった時間が格納されています（infで初期化。親ならinfのまま）。
ある時間tにおいてmerge_times[x]を確認し、tより大きい場合、その時点ではxは親であったことがわかるため、xがその時刻における集合の根となります。
一方で、merge_times[x]がt以下の場合、xはその時点で子であり、親が存在するのでpar[x]を参照して再帰的に親を探します。
根を辿る過程で経路圧縮などのparを書き換える操作は行いません（関係が破綻するので）。そのため計算量は$O(\log{N})$となります。

• 例：_find_root(t = 3, x = 4)
  • merge_times[x = 4] = 2なので、x = 4はt = 2時点で誰かの子になっている。なのでx = par[x = 4] = 2に移動する
  • _find_root(t = 3, x = 2)を呼ぶ
    • merge_times[x = 2] = 4なので、x = 2はt = 2時点ではまだ親（t = 4で初めて誰かの子になる）なのでreturn x = 2を返す

再帰実装

    def _find_root(self, t: int, x: int) -> int:
        if self.merge_times[x] > t:
            return x
        return self._find_root(t, self.par[x])

非再帰実装

    def _find_root(self, t: int, x: int) -> int:
        while self.merge_times[x] <= t:
            x = self.par[x]
        return x

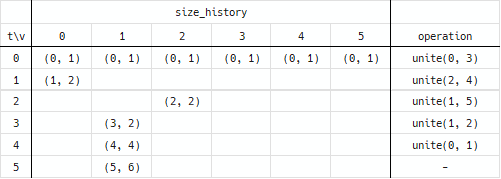
size_historyの遷移

• get_size関数を実装するために必要
• unite(x, y)の際に親の根rx側にuniteした時間とその時のsizeを保存していきます
  • 例：要素数5の集合rxと、要素数3の集合ryとを併合
    • →size_history[rx].append((cur_time, -par[rx]))
    • -par[rx]は8（5+3）

• [[(0, 1)], [(0, 1)], [(0, 1)], [(0, 1)], [(0, 1)], [(0, 1)]]
  • 初期状態ではすべての要素がサイズ1の自分自身を根として持っている
• [[(0, 1), *(1, 2)*], [(0, 1)], [(0, 1)], [(0, 1)], [(0, 1)], [(0, 1)]]
  • unite(0, 3)→根である0側に時間とsize(1, 2)が保存
• [[(0, 1), (1, 2)], [(0, 1)], [(0, 1), *(2, 2)*], [(0, 1)], [(0, 1)], [(0, 1)]]
  • unite(2, 4)→根である2側に時間とsize(2, 2)が保存
• [[(0, 1), (1, 2)], [(0, 1), *(3, 2)*], [(0, 1), (2, 2)], [(0, 1)], [(0, 1)], [(0, 1)]]
  • unite(1, 5)→根である1側に時間とsize(3, 2)が保存
• [[(0, 1), (1, 2)], [(0, 1), (3, 2), *(4, 4)*], [(0, 1), (2, 2)], [(0, 1)], [(0, 1)], [(0, 1)]]
  • unite(1, 2)→根である1側に時間とsize(4, 4)が保存
• [[(0, 1), (1, 2)], [(0, 1), (3, 2), (4, 4), *(5, 6)*], [(0, 1), (2, 2)], [(0, 1)], [(0, 1)], [(0, 1)]]
  • unite(0, 1)→根である1側に時間とsize(5, 6)が保存
  • これですべての要素が併合された

get_sizeの仕組み

• ある時刻tにおいて要素xが属する集合のサイズを求めるために呼び出します
• size_historyには自分が親だったときの、各併合が行われた(時刻, 要素数)が保存されています
• よって時刻tにおけるxの親rxが特定できれば、size_history[rx]の情報からget_size(t, x)を求めることができます
  • 具体的には時刻t以前で最近行われた併合がわかれば、その時の要素数が求めたい答え
  • size_historyの各値は併合の時刻について昇順に並んでいるので、時刻tの境界を二分探索で高速に探索できます
    • 二分探索部分はbisectに置き換えられます。ちょっとコードが短くなります

    def get_size(self, t: int, x: int) -> int:
        # 1. 時刻tにおける親rxを求める
        rx = self._find_root(t, x)
        
        # 2. size_history[rx]内で、時刻t以前に行われた併合に関する情報の場所を探索
        is_valid = lambda x: self.size_history[rx][x][0] <= t
        idx = self._binary_search(0, len(self.size_history[rx]), is_valid)
        
        # 3. 探索した併合情報におけるsizeを返す
        return self.size_history[rx][idx][1]

get_merge_timeの仕組み

• 2要素x, yが、どの時刻で併合されたのか調べたい場合に呼び出します
• 最新の時刻において併合されていないのであれば、それ以前においても当然併合されていないのでget_merge_timeは定義できませんので、便宜上-1を返します
  • これはis_same(cur_time, x, y)により判定可能
• そうでない場合は、現在時刻以前に併合されています
  • 併合時間はt = 0を大きくしながらis_same(t, x, y)を調べれば、どこかのタイミングでTrueとなるのでその時刻を返せばいいです（線分探索）
  • is_same(t, x, y)は併合時刻以前はFalse、以後はTrueとなるので、二分探索が使えます

    def get_merge_time(self, x: int, y: int) -> int:
        # 最新の時刻で併合されていなければ -1 を返す
        if not self.is_same(self.cur_time, x, y):
            return -1

        # 併合された時刻を二分探索で見つける
        is_valid = lambda t: self.is_same(t, x, y)
        return self._binary_search(self.cur_time, -1, is_valid)

要素列挙機能の追加

やっと本題です。
ここでの追加点は、時間$t$における、要素$x$が含まれる集合の要素列挙機能です。具体的には、新しいインスタンス変数next_vと追加メソッド_find_next、get_set_membersを追加実装します。
まずは全体を見てみましょう。違いはハイライト部分だけです。

class PartiallyPersistentDisjointSet:
    INF = 1 << 60

    def __init__(self, N: int) -> None:
        self.cur_time = 0
        self.par = [-1] * N
        self.merge_times = [self.INF] * N
        self.size_history = [[(0, 1)] for _ in range(N)]
+       self.next_v = [[(0, i)] for i in range(N)]

    def _find_root(self, t: int, x: int) -> int:
        while self.merge_times[x] <= t:
            x = self.par[x]
        return x

    def unite(self, x: int, y: int) -> bool:
        rx = self._find_root(self.cur_time, x)
        ry = self._find_root(self.cur_time, y)
        self.cur_time += 1
        if rx == ry:
            return False
        if self.par[rx] > self.par[ry]:
            rx, ry = ry, rx
        self.par[rx] += self.par[ry]
        self.par[ry] = rx
        self.merge_times[ry] = self.cur_time
        self.size_history[rx].append((self.cur_time, -self.par[rx]))

+       # next_vの更新
+       next_rx = self.next_v[rx][-1][1]
+       next_ry = self.next_v[ry][-1][1]
+       self.next_v[rx].append((self.cur_time, next_ry))
+       self.next_v[ry].append((self.cur_time, next_rx))

        return True

    def is_same(self, t: int, x: int, y: int) -> bool:
        return self._find_root(t, x) == self._find_root(t, y)

    @staticmethod
    def _binary_search(ok, ng, is_valid):
        while abs(ok - ng) > 1:
            mid = (ok + ng) >> 1
            if is_valid(mid):
                ok = mid
            else:
                ng = mid
        return ok

    def get_size(self, t: int, x: int) -> int:
        rx = self._find_root(t, x)
        is_valid = lambda x: self.size_history[rx][x][0] <= t
        idx = self._binary_search(0, len(self.size_history[rx]), is_valid)
        return self.size_history[rx][idx][1]

    def get_merge_time(self, x: int, y: int) -> int:
        if not self.is_same(self.cur_time, x, y):
            return -1
        is_valid = lambda z: self.is_same(z, x, y)
        return self._binary_search(self.cur_time, -1, is_valid)

+   def _find_next(self, t: int, x: int) -> int:
+       is_valid = lambda i: self.next_v[x][i][0] <= t
+       idx = self._binary_search(0, len(self.next_v[x]), is_valid)
+       return self.next_v[x][idx][1]

+   def get_set_members(self, t: int, x: int) -> list[int]:
+       rx = self._find_root(t, x)
+       members = [rx]
+       cv = self._find_next(t, rx)
+       while cv != rx:
+           members.append(cv)
+           cv = self._find_next(t, cv)
+       return members

追加インスタンス変数

• next_v = [[(0, i)] for i in range(N)]
  • 循環リストの「次の要素」を管理する配列
  • ある集合$X,Y$を併合するとき、それらの根をrx, ryとして、それらの根の「次の要素」を入れ替える
  • 空間：$O(N+M)$（後述）

追加メソッド

• $N$：集合の要素数
• $M$：操作回数
• _find_next(t: int, x: int) -> int:
  • 時刻$t$における要素$x$の「次の要素」を探索する
  • 時間：$O(\log{M})$
• get_set_members(t: int, x: int) -> list[int]:
  • 時刻$t$における要素$x$と同じ素集合に属する全ての要素を返す
  • 時間：$O(k\log{M})$（Output-sensitive）
    • $k$：返される集合の要素数（最悪$N$）

next_vの遷移

• unite(x, y)時にnext_vへappendする
  • これは$O(1)$で可能なのでuniteの計算量は変わらない

• [[(0, 0)], [(0, 1)], [(0, 2)], [(0, 3)], [(0, 4)], [(0, 5)]]
  • 初期状態では全ての要素が自分を次の要素とする循環リストになっている
• [[(0, 0), (1, 3)], [(0, 1)], [(0, 2)], [(0, 3), (1, 0)], [(0, 4)], [(0, 5)]]
  • unite(0, 3)→next_v[0]に(1, 3)、next_v[3]に(1, 0)を格納。時刻t = 1における循環リスト情報を記録
  • これで時刻1において0→3→0という循環リストが構成された
• [[(0, 0), (1, 3)], [(0, 1)], [(0, 2), (2, 4)], [(0, 3), (1, 0)], [(0, 4), (2, 2)], [(0, 5)]]
  • unite(2, 4)→next_v[2]に(2, 4)、next_v[4]に(2, 2)を格納。
  • これで時刻2において2→4→2という循環リストが構成された
• [[(0, 0), (1, 3)], [(0, 1), (3, 5)], [(0, 2), (2, 4)], [(0, 3), (1, 0)], [(0, 4), (2, 2)], [(0, 5), (3, 1)]]
  • unite(1, 5)→next_v[1]に(3, 5)、next_v[5]に(3, 1)を格納。
  • これで時刻3において1→5→1という循環リストが構成された
• [[(0, 0), (1, 3)], [(0, 1), (3, 5), (4, 4)], [(0, 2), (2, 4), (4, 5)], [(0, 3), (1, 0)], [(0, 4), (2, 2)], [(0, 5), (3, 1)]]
  • unite(1, 2)→next_v[1]に(4, 4)、next_v[2]に(4, 5)を格納。
  • これで時刻4において1→4→2→5→1という循環リストが構成された
• [[(0, 0), (1, 3), (5, 4)], [(0, 1), (3, 5), (4, 4), (5, 3)], [(0, 2), (2, 4), (4, 5)], [(0, 3), (1, 0)], [(0, 4), (2, 2)], [(0, 5), (3, 1)]]
  • unite(0, 1)→next_v[0]に(5, 4)、next_v[1]に(5, 3)を格納。
  • これで時刻5において1→3→0→4→2→5→1という循環リストが構成された

next_vの空間計算量

• 初期状態ではnext_vは要素数$N$で初期化される
• unite1回につき2要素増えるので、unite$M$回で$2M$増える→よって空間計算量は$O(N+M)$
  • 上の例だと要素数$N=6$、uniteが5回で$M=5$なので、最終的な要素数は$N+2M=6+2 \times 5 = 16$となっている

_find_nextの仕組み

• next_v[x]からある時刻tにおける循環リストの「次の要素」を探索する
• これはnext_v[x]を二分探索すればいいだけです。上の図をあるxの列で見たときのtupleの最初の要素が時刻tの境界になるところを探しています

    def _find_next(self, t: int, x: int) -> int:
        is_valid = lambda i: self.next_v[x][i][0] <= t
        idx = self._binary_search(0, len(self.next_v[x]), is_valid)
        return self.next_v[x][idx][1]

get_set_membersの仕組み

• 時刻tにおける要素xが含まれる素集合の要素を列挙する
• 基本的には前回記事「要素列挙可能Union Findの実装例」のグループを陰に持つ実装と同じです
• 要素xの時刻tにおける「次の要素」をfind_next(t, x)によって見つけることを、「次の要素」が要素tと一致するまで繰り返せば、時刻tにおける循環リストの要素を列挙できます
  • 例：get_set_members(t=4, x=5)
    • rx = self._find_root(4, 5) = 1
    • members = [1]
    • cv = self._find_next(4, 1) = 4
    • ループ1: members = [1, 4], cv = self._find_next(4, 4) = 2
    • ループ2: members = [1, 4, 2], cv = self._find_next(4, 2) = 5
    • ループ3: members = [1, 4, 2, 5], cv = self._find_next(4, 5) = 1
    • ループ終了（cv == rx）
    • 返り値: [1, 4, 2, 5]

    def get_set_members(self, t: int, x: int) -> list[int]:
        rx = self._find_root(t, x)
        members = [rx]
        cv = self._find_next(t, rx)
        while cv != rx:
            members.append(cv)
            cv = self._find_next(t, cv)
        return members

動作チェック用unit test

varifyできる問題がなかったので動作確認のためにunit testを作成しました。
多分これでチェックできているはず...

import unittest
import random


class TestPartiallyPersistentDisjointSet(unittest.TestCase):
    def setUp(self):
        self.N = 5
        self.ppds = PartiallyPersistentDisjointSet(self.N)

    # get_set_memberのテスト
    def test_initial_state(self):
        for i in range(5):
            self.assertEqual(self.ppds.get_set_members(0, i), [i])

    def test_single_union(self):
        self.ppds.unite(0, 1)
        self.assertSetEqual(set(self.ppds.get_set_members(0, 0)), {0})
        self.assertSetEqual(set(self.ppds.get_set_members(1, 0)), {0, 1})
        self.assertSetEqual(set(self.ppds.get_set_members(1, 1)), {0, 1})

    def test_multiple_unions(self):
        self.ppds.unite(0, 1)
        self.ppds.unite(2, 3)
        self.ppds.unite(0, 2)

        self.assertSetEqual(set(self.ppds.get_set_members(3, 0)), {0, 1, 2, 3})
        self.assertSetEqual(set(self.ppds.get_set_members(3, 1)), {0, 1, 2, 3})
        self.assertSetEqual(set(self.ppds.get_set_members(3, 2)), {0, 1, 2, 3})
        self.assertSetEqual(set(self.ppds.get_set_members(3, 3)), {0, 1, 2, 3})
        self.assertEqual(self.ppds.get_set_members(3, 4), [4])

    def test_historical_queries(self):
        self.ppds.unite(0, 1)  # time 1
        self.ppds.unite(2, 3)  # time 2
        self.ppds.unite(0, 2)  # time 3

        self.assertSetEqual(set(self.ppds.get_set_members(1, 0)), {0, 1})
        self.assertSetEqual(set(self.ppds.get_set_members(2, 2)), {2, 3})
        self.assertSetEqual(set(self.ppds.get_set_members(2, 0)), {0, 1})
        self.assertSetEqual(set(self.ppds.get_set_members(3, 0)), {0, 1, 2, 3})

    def test_all_elements_united(self):
        self.ppds.unite(0, 1)
        self.ppds.unite(1, 2)
        self.ppds.unite(2, 3)
        self.ppds.unite(3, 4)

        expected_set = set(range(5))
        for i in range(5):
            self.assertSetEqual(set(self.ppds.get_set_members(4, i)), expected_set)

    def test_get_set_members_random(self):
        N = 1000  # 頂点数
        M = 1000  # 操作回数
        ds = PartiallyPersistentDisjointSet(N)
        naive_groups = [[[i] for i in range(N)] for _ in range(M + 1)]
        roots = [[*range(N)] for _ in range(M + 1)]

        for _ in range(M):
            x = random.randint(0, N - 1)
            y = random.randint(0, N - 1)
            ds.unite(x, y)

            # naive計算part
            # 各時間でグループを陽に持つ計算をする
            t = ds.cur_time
            rx = ds._find_root(t - 1, x)
            ry = ds._find_root(t - 1, y)
            if rx == ry:
                continue
            if len(naive_groups[t][rx]) < len(naive_groups[t][ry]):
                rx, ry = ry, rx
            naive_groups[t][rx].extend(naive_groups[t][ry])
            for i in naive_groups[t][ry]:
                roots[t][i] = rx
            naive_groups[t][ry].clear()
            # print(f"{naive_groups[t] = }")
            naive_groups[t + 1] = [s[:] for s in naive_groups[t]]
            roots[t + 1] = roots[t][:]

        # ランダムな要素でget_set_memberをテスト
        for _ in range(1000):
            x = random.randint(0, N - 1)
            t = random.randint(0, ds.cur_time)
            expected_member = set(naive_groups[t][roots[t][x]])
            actual_member = set(ds.get_set_members(t, x))

            self.assertEqual(
                actual_member,
                expected_member,
                f"Failed for x={x}, t={t}. Expected {expected_member}, got {actual_member}",
            )


if __name__ == "__main__":
    unittest.main()

結び

というわけで一般的な部分永続UnionFindに任意時間の要素列挙機能を追加した実装を紹介しました。
ちょっと調べたけど類似の実装例が見つからないので新規性はあると思います。そうだったらいいな（そもそも需要が無いのかもしれないけど）。
さらなる最適化や応用の可能性も考えられるので、興味のある方はぜひ実装を試してみてください。
記事が有益と感じたら「いいね」押してね。記事作成の励みになりますので。

Verification

• H - Union Sets
  • get_merge_timeの動作確認用
• D - Stamp Rally
  • get_sizeの動作確認用
  • かなり時間がギリギリ
• O - 可変全域木
  • get_merge_timeの動作確認用
• Partially Persistent DSU

References

• 部分永続UnionFindについて
  • pythonで永続UnionFind実装 - Qiita
  • やぶについて書きます
  • Partial Persistent Union Find My Algorithm : kopricky アルゴリズムライブラリ
• 循環リストについて
  • 解説 - 第10回 アルゴリズム実技検定 過去問
  • 素集合の要素の列挙と併合 (単方向循環リスト) - noshi91のメモ
  • 要素列挙可能Union Findの実装例