k-means++とMMSK-meansのパフォーマンス比較

ZOZOテクノロジーズその２ Advent Calendar 2018 の1日目の記事になります。
今回は、k-meansアルゴリズムを考える上で重要なクラスターセンターの初期値について調べたことを述べたいと思います。

はじめに

k-menas法はデータのクラスタリングをする際に用いられる定番のアルゴリズムです。意味の近いデータ点をまとめたり、データを分類することでデータの構造を把握するといった用途に用いることがあります。

最近読んだ論文 "Tag clustering algorithm LMMSK: Improved K-means algorithm based on latent semantic analysis" の中でデータの類似度行列を使ったk-meansの初期値決定アルゴリズム（Min Max Similarity K-Means:MMSK-means）が提案されていました。一方で、k-meansの初期値を決める方法としてk-means++という定番のものがあります。論文中ではMMSK-meansとk-means++のパフォーマンスの比較がなかったため、その良さがわかりませんでした。そこで今回の記事では、MMSK-meansのアルゴリズムを実装し、k-means++のパフォーマンスと比較します。パフォーマンスを測る観点として、収束に至るまでのイテレーション回数と、クラスター内の二乗誤差（Error Sum of Squares:SSE）を見ることにします。

アルゴリズム

MMSK-meansのアルゴリズムについて説明します。k-means++ の説明は他の記事に譲ります。

MMSK-means

MMSK-meansはデータの類似度を利用したクラスターセンターの初期値の決定方法です。
具体的には以下のステップで初期値が決定されます。

step1. 各データ点をノルムにより正規化する
step2. 全データ点のペアの類似度が要素になる、類似度行列を計算する
step3. 類似度行列の中でもっとも類似度の低い2点をクラスター中心点とする
step4. 各データ点とクラスター中心点のペアのうち、もっとも類似度が大きくなるようなクラスター中心点との類似度を計算する
step5. step4で得られた類似度のうちもっとも類似度が低い点を新しいクラスター中心点とする
step6. step4とstep5を必要なクラスター中心点が揃うまで繰り返す

通常のk-meansやk-means++のように乱数を使わないため、MMSK-meansはデータセットに対して必ず同じ初期値が選ばれることになります。論文ではノルムによって正規化したデータの類似度行列を使って初期値を選んでいました。しかし、問題設定によってはユークリッド距離行列による選び方の方が適切である場合が多いと感じたので、step1を省略し、MMSK-meansと同じ発想でユークリッド距離行列を利用し初期値を選ぶアルゴリズムを実装し、使っています。

MMSK-means (Euclid distance matrix version)

import numpy as np
from sklearn.metrics.pairwise import euclidean_distances

# MMSK-means (euclid distance matrix)
def initial_centroid_via_euclidean_distance_matrix(data, n_clusters):
    # 距離行列を計算
    dist_mat = euclidean_distances(data, data)

    # 最初の２つのクラスタセンターを探す
    centroid_index = np.where(dist_mat == dist_mat.max())[0]

    # クラスタセンターと各データ点の距離行列を取得
    temp = dist_mat[centroid_index]

    # クラスタセンターの候補から外す
    temp[np.where(temp == temp.max())] = 0

    # 必要なクラスタセンターが集まるまで繰り返す
    while n_clusters > len(centroid_index):
        # 新しいクラスタセンターを追加
        centroid_index = np.append(centroid_index,
                                   temp.min(axis=0).argmax())
        temp = np.append(temp,
                         [dist_mat[temp.min(axis=0).argmax()]],
                         axis=0)
        temp[:, centroid_index] = 0
    cluster_centers = data[centroid_index]

    return cluster_centers

実際に選ばれる初期値

以下の９つの島の中心が格子状に分布している以下のようなデータで、各アルゴリズムが選ぶ初期値を見てみます。

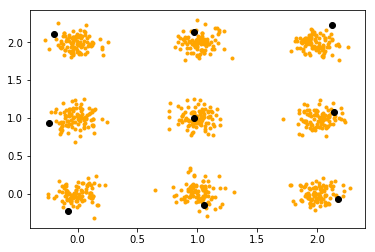
k-means (random)

ランダムに選んだ初期値を黒点で示しています。ランダムに初期値を選ぶと偏りが生じてしまい、想定する島を捉えることができていません。

k-means++

k-means++はすでに選ばれた初期値とデータ点の距離を重み付けして選ぶ方法ですが、それぞれの島に初期値が選ばれていることがわかります。k-meansよりも収束が早く、精度が高いと言われている理由はこのような観察からも理解できます。

MMSK-means

MMSK-meansも、k-means++と同様に初期値の時点で９つの島を捉えることができています。これも単純なランダムよりも収束が早く、精度が高くなることが期待できそうです。

実装

評価のために新たにKMeansクラスを実装しました。クラスタセンターの初期化関数を3つ用意し選べるようにしています。

import numpy as np
import random
from sklearn.metrics.pairwise import euclidean_distances


class KMeans(object):

    def __init__(self, n_clusters, max_iter, init):
        self.n_clusters = n_clusters
        self.max_iter = max_iter
        self.cluster_centers = None
        self.init = init

    def _init_cluster_centers_mms(self, data):
        dist_mat = euclidean_distances(data, data)
        centroid_index = np.where(dist_mat == dist_mat.max())[0]
        temp = dist_mat[centroid_index]
        temp[np.where(temp == temp.max())] = 0
        while self.n_clusters > len(centroid_index):
            centroid_index = np.append(centroid_index, temp.min(axis=0).argmax())
            temp = np.append(temp, [dist_mat[temp.min(axis=0).argmax()]], axis=0)
            temp[:, centroid_index] = 0
        self.cluster_centers = data[centroid_index]

    def _init_cluster_centers_random(self, data):
        random_index = random.sample(range(len(data)), self.n_clusters)
        self.cluster_centers = data[np.array(random_index)]

    def _init_cluster_centers_pp(self, data):
        centroid_index = np.array([random.randint(0, len(data) - 1)])
        dist_mat = euclidean_distances(data, data[centroid_index])
        centroid_index = np.append(
            centroid_index,
            np.random.choice(
                len(data),
                1,
                p=np.reshape(
                    (dist_mat**2 / sum(dist_mat**2)),
                    (len(data),))))

        while self.n_clusters > len(centroid_index):
            dist_mat = euclidean_distances(data, data[centroid_index])
            dist_mat_pooling = dist_mat.min(axis=1)
            centroid_index = np.append(
                centroid_index,
                np.random.choice(
                    len(data),
                    1,
                    p=np.reshape(
                        (dist_mat_pooling**2 / sum(dist_mat_pooling**2)),
                        (len(data),))))
        self.cluster_centers = data[centroid_index]

    def _one_iter(self, data):

        self.pred = np.array([
            np.array([
                self._euclidean_distance(p, centroid)
                for centroid in self.cluster_centers
            ]).argmin()
            for p in data
        ])
        self.cluster_centers = np.array([data[self.pred == i].mean(axis=0)
                                         for i in range(self.n_clusters)])

    def fit_predict(self, data):
        tmp_pred = np.random.randint(0, self.n_clusters, len(data))

        if self.init == 'mms':
            self._init_cluster_centers_mms(data)
        elif self.init == 'pp':
            self._init_cluster_centers_pp(data)
        elif self.init == 'random':
            self._init_cluster_centers_random(data)

        for i, _ in enumerate(range(self.max_iter)):
            self._one_iter(data)
            if (tmp_pred == self.pred).all():
                break
            tmp_pred = self.pred
        return i

    def _euclidean_distance(self, p0, p1):
        return np.sum((p0 - p1) ** 2)

評価

収束するまでにかかるイテレーション数と、クラスター内二乗誤差の総和の観点からk-means, k-means++, MMSK-meansのパフォーマンスを評価しました。それぞれ50回アルゴリズムを実行し、平均値を取っています。この表からどちらの基準でもMMSK-meansが良い成果を出していることがわかります。単に精度が高いだけでなく、収束も早くなるとしたらとても使えるアルゴリズムである可能性があります。今回は時間の都合上、様々なデータセットで評価することができていないので、一概にMMSK-meansが優れているとは言えませんので注意が必要です。

初期化アルゴリズム	平均クラスタ内二乗誤差	収束までの平均イテレーション数
k-means(random)	236.1320	23.44
k-means++	235.7725	21.62
MMSK-means	232.4732	18.48

まとめ

k-meansの初期値決定アルゴリズムであるMMSK-meansのパフォーマンスを簡単にですが検証しました。今回調査したデータセットでは、収束速度とクラスター内二乗誤差の観点から、MMSK-meansが良さそうだということがわかりました。安易にMMSK-meansを利用することはお勧めできませんが、選択肢の一つにはなるのかもしれません。検証の手間など考えると、実際にはすでに高い実績を誇るk-means++を利用した方が良い場面が多いと思います。