量子コンピュータ Advent Calendar 2021 の1日目の記事を担当することになった algas です。
誤り耐性万能量子コンピュータに関わる量子計算の基礎知識を入門者向けに解説する内容になっています。
先日 Nature で発表された量子誤り耐性の論文 Egan, L. et al. Fault-tolerant control of an error-corrected qubit. (2021) を読もうとしたけど初見では理解できませんでした。勉強して理解できるようになったので、その学習過程で得た知識を共有したいと思います。
想定読者
次のような読者を想定しています。
- 量子誤り耐性や万能量子計算に興味がある
- 量子ビットや量子ゲートがどんなものか知っている
- 簡単なブラケット記法が読める
これから量子コンピュータを勉強される方で本記事の記述が理解できない場合には、量子コンピュータ超入門やその他の量子コンピュータの入門書などを一読してから本記事を読み直すと理解できるはずです。
量子コンピュータのハードウェアや具体的なソフトウェアによる実装は本記事では取り扱いません。
背景
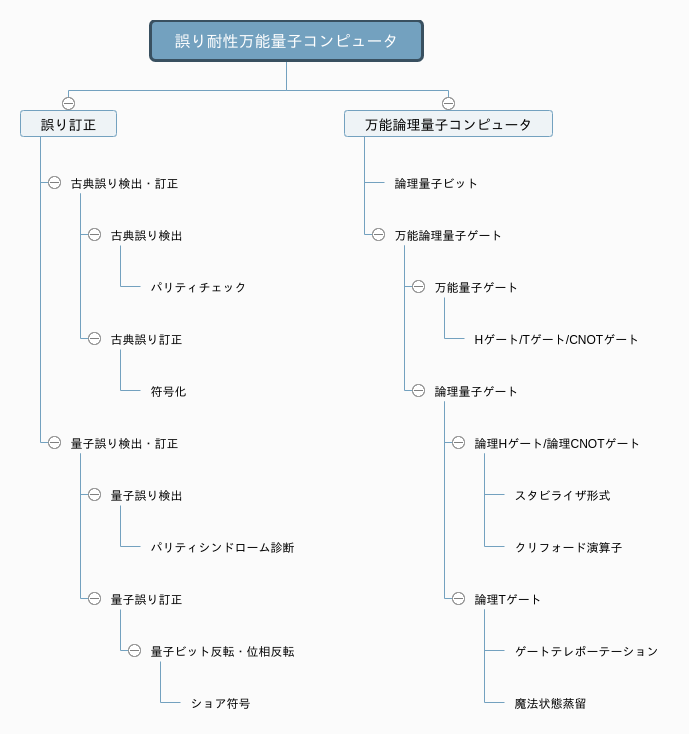
量子コンピュータの世界の理想の1つに誤り耐性万能量子コンピュータの実現があります。
ノイズの多い現実世界の量子コンピュータの信頼性を高めるためには量子ビットに誤り訂正を施す必要があります。量子誤り訂正を行うために複数の量子ビットを冗長符号化して1つの論理量子ビットを作ります。一部の量子ビットがエラーで反転しても誤り訂正を施すことで誤り耐性をもたせることができます。物理量子ビットに対応する物理量子ゲートがあるように、論理量子ビットに対応するのが論理量子ゲートです。この論理量子ゲートを任意の量子ゲート操作に対応させたものが万能論理量子ゲートです。
本記事では誤り耐性万能量子コンピュータを実現するために必要な技術要素を解説します。
要素の関係をわかりやすくするために図にしてみました。
各要素の詳細については記事内で説明します。
誤り訂正
量子誤り訂正の前にまずは古典ビットに対する誤り検出・誤り訂正を紹介します。それから量子誤り訂正の要素としてパリティシンドローム診断による量子誤り検出、ビット反転と位相反転、ショア符号を解説します。
古典誤り検出
古典コンピュータのデータにおける誤り検出の1つの方法としてパリティチェックがあります。
パリティとはビットの「0」もしくは「1」の数が偶数か奇数かを判断することをいいます。
たとえば7ビットのデータを送るときに「1」の数が偶数になるように末尾に1ビットを加えて8ビットとして送るとします。
「1100101」(7 bits) → 「11001010」(8 bits)
「1101110」(7 bits) → 「11011101」(8 bits)
もし8ビットの「1」の数の合計が奇数になっていたらノイズが入ってデータが間違っているとわかります。
ただし、この方法では奇数個のビットにノイズが含まれているときだけ正しく検出されます。
古典誤り訂正
同じビットを繰り返し符号を用いて冗長度を上げる誤り訂正の手法があります。
たとえば
「0」の信号を送るときは「000」
「1」の信号を送るときは「111」
のように繰り返します。
このとき「000」「111」などを符号語といいます。
「010」「101」のような信号が一致していないデータになっているときはノイズが入っているとみなします。
多数決ルールによって復号化訂正を行います。
「100」「010」→「0」
「110」「101」→「1」
この場合、高々1つのビットにノイズが入っているときしか訂正できません。
符号語「000」と「111」を相互に変換するには3回のビット反転が必要です。
符号語の変換に必要な操作回数を符号距離といいます。
つまり符号距離 d=3 となります。
一般に符号距離の半分未満までしか誤り訂正できません。
量子ビット反転と位相反転
古典ビットではエラーによって「0」か「1」かのビットの反転が起こります。量子ビットではビットだけではなくて位相の反転も発生します。
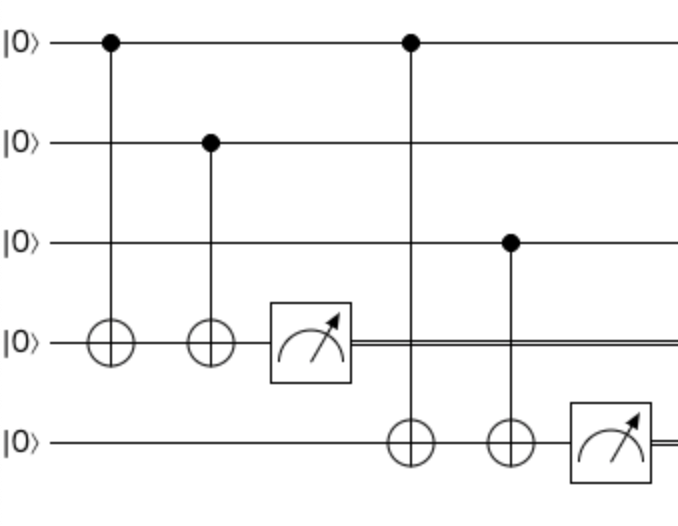
量子ビットのパリティシンドローム診断
古典コンピュータではパリティは簡単に判定できますが、量子コンピュータの場合には観測すると量子状態が壊れてしまうので観測せずに判定する工夫が必要です。
量子3ビットが $ \vert000\rangle $ か $ \vert111\rangle $ の状態であるときいずれかのビット1つがエラーによってビット反転してしまうことを想定します。
このとき上の3つの量子ビットを観測することなく、そのパリティを下の2つの量子補助ビットで診断します。
コントロール量子ビット(黒丸)とターゲット量子ビット(白丸十字)をつなぐ線がCNOTゲートを表します。
コントロール量子ビットが $ \vert1\rangle $ のときだけターゲット量子ビットの値をビット反転します。
回路図の記号で指示針の図が測定を表します。
- 量子補助ビットが $ \vert00\rangle $ のときは反転なし
\vert000\rangle\vert00\rangle \rightarrow \vert000\rangle\vert00\rangle \\
\vert111\rangle\vert00\rangle \rightarrow \vert111\rangle\vert00\rangle
- 量子補助ビットが $ \vert01\rangle $ のときは上から3番目のビットが反転してる
\vert001\rangle\vert00\rangle \rightarrow \vert001\rangle\vert01\rangle \\
\vert110\rangle\vert00\rangle \rightarrow \vert110\rangle\vert01\rangle
- 量子補助ビットが $ \vert10\rangle $ のときは上から2番目のビットが反転してる
\vert010\rangle\vert00\rangle \rightarrow \vert010\rangle\vert10\rangle \\
\vert101\rangle\vert00\rangle \rightarrow \vert101\rangle\vert10\rangle
- 量子補助ビットが $ \vert11\rangle $ のときは上から1番目のビットが反転してる
\vert100\rangle\vert00\rangle \rightarrow \vert100\rangle\vert11\rangle \\
\vert011\rangle\vert00\rangle \rightarrow \vert011\rangle\vert11\rangle
量子ビットの誤り訂正
量子ビットを冗長符号化してパリティシンドローム診断の結果と組み合わせて復号化をすることで量子ビットに誤り訂正を施すことができます。
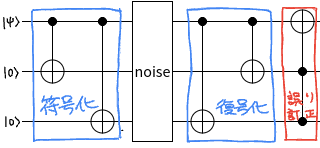
ビット反転の量子誤り訂正ゲート
量子1ビットから量子3ビットに符号化した量子ビットに高々1ビットのビット反転ノイズが乗るものとします。復号化してビット反転誤り訂正を行う回路を示します。
まずCNOTゲートを使って量子ビットの情報を量子3ビットへ符号化します。
(\alpha\vert0\rangle + \beta\vert1\rangle)\vert00\rangle \rightarrow \alpha\vert000\rangle + \beta\vert111\rangle
この符号化した量子ビットにビット反転ノイズが乗ります。
その後で復号化してビット反転誤り訂正をします。
回路図の一番右のゲートがトフォリゲートです。2つのコントロール量子ビット(黒丸)の両方とも $ \vert1\rangle $ のときだけターゲット量子ビット(白丸十字)の値をビット反転します。
\alpha\vert000\rangle+\beta\vert111\rangle \rightarrow (\alpha\vert0\rangle+\beta\vert1\rangle)\alpha\vert00\rangle \\
\alpha\vert001\rangle+\beta\vert110\rangle \rightarrow
(\alpha\vert0\rangle+\beta\vert1\rangle)\alpha\vert01\rangle \\
\alpha\vert010\rangle+\beta\vert101\rangle \rightarrow (\alpha\vert0\rangle+\beta\vert1\rangle)\alpha\vert10\rangle \\
\alpha\vert100\rangle+\beta\vert011\rangle \rightarrow (\alpha\vert0\rangle+\beta\vert1\rangle)\alpha\vert11\rangle
各ビットが1つ反転している場合においてもすべて $ \alpha\vert0\rangle+\beta\vert1\rangle $ の形に訂正されていることがわかります。
位相反転の量子誤り訂正ゲート
基本的にはビット反転の量子誤り訂正と同じ形をしています。
符号化の後および復号化の前にアダマールゲート(H)を施すことでビット反転と位相反転を相互変換しています。
H\vert0\rangle = \vert+\rangle, H\vert1\rangle = \vert-\rangle
- 符号化の後
\alpha\vert000\rangle+\beta\vert111\rangle \rightarrow \alpha\vert+++\rangle+\beta\vert---\rangle
- 復号化の前
\alpha\vert+++\rangle+\beta\vert---\rangle \rightarrow
\alpha\vert000\rangle+\beta\vert111\rangle
位相反転エラーによって「+」と「-」が逆になっても、量子誤り訂正ゲートによって元に戻されます。
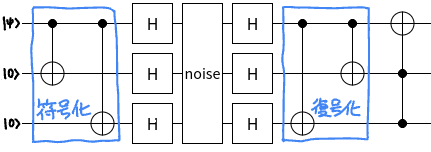
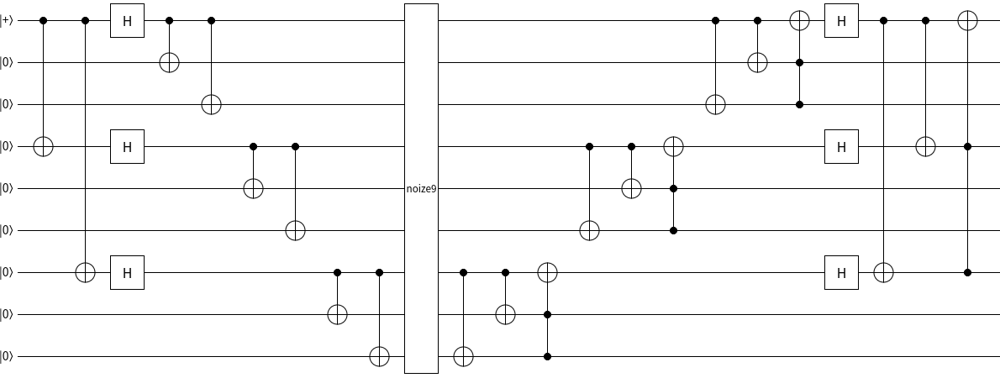
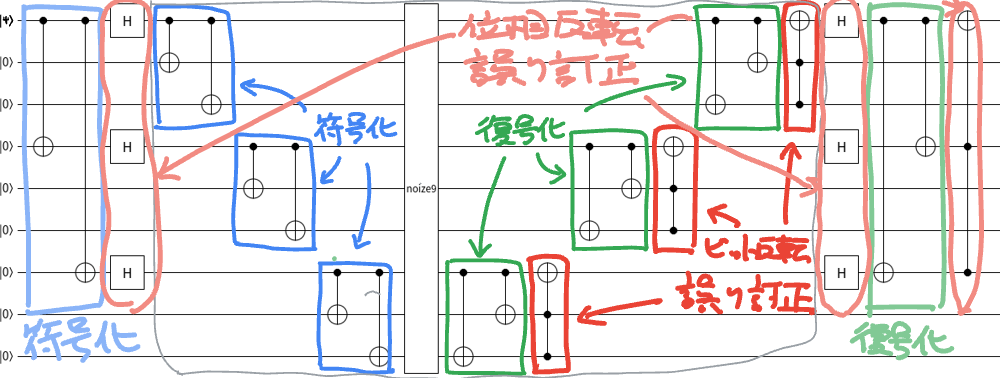
ショア符号
量子9ビットを使ってビット反転と位相反転の量子誤り訂正をする回路がショア符号(shor code)です。一見複雑そうに見えますが、上記で説明したビット反転と位相反転を組み合わせたものになっています。
下が解説つきの図です。
アダマールゲートより内側の回路がビット反転量子誤り訂正をしていて、アダマールゲートとその外側の回路で位相反転の量子誤り訂正を行います。
万能論理量子ゲート
万能論理量子ゲートは論理量子ビットに施す万能量子ゲートのことです。万能ゲートは任意のゲートを実現するための要素となるゲートであり、万能古典ゲートとしてNANDゲートが知られています。つまり、NANDゲートだけの組み合わせで任意の古典ゲートが実現できます。同様に万能量子ゲートとしてCNOTゲートとH,Tゲートがあります。CNOTゲートとH,Tゲートの組み合わせによって(理論的には)任意の量子ゲートが実現できます。
万能論理量子ゲートのためにクリフォード演算子と魔法状態蒸留を解説します。クリフォード演算子から論理CNOTゲートとHゲートを示し、魔法状態蒸留によって論理Tゲートを実現します。
万能量子ゲート
万能古典ゲートはNANDゲート1つで十分ですが、万能量子ゲートは複数のゲートの組み合わせが必要です。
1ビット量子ゲートとしてアダマール(H)ゲートとTゲート、2ビット量子ゲートとしてCNOTゲートの組み合わせで任意の量子ゲートの機能を理論的には再現できます。
論理量子ビット
論理量子ビットとは冗長符号化のために複数の物理量子ビットで構成されます。
一般的には誤り訂正によって量子ビットに生じる誤りを検出して訂正するために符号化します。
論理量子ゲートへの導入としてスタビライザ形式を解説します。
論理量子ゲート
論理量子ゲートは論理量子ビットに作用させるゲートです。論理量子ビットが複数の物理量子ビットを使うのと同様に複数の物理量子ゲートを組み合わせて論理量子ビットに対して演算を行えるようにします。
スタビライザ形式
論理量子ビットに対する演算、すなわち論理量子ゲートを記述しやすくするためにスタビライザ形式を導入します。
n量子ビット状態を表す1つ方法としてスタビライザ形式があります。
まずパウリ群を定義します。パウリ群はパウリ演算子(X,Y,Zゲート)と $ I $ の積に $ \pm $ か $ \pm i $ の符号をつけたものです。
X = \left[\begin{matrix} 0&1 \\ 1&0 \end{matrix}\right], Y = \left[\begin{matrix} 0&-i \\ i&0 \end{matrix}\right], Z = \left[\begin{matrix} 1&0 \\ 0&-1 \end{matrix}\right] \\
P(n) = \lbrace\pm 1,\pm i\rbrace \times \lbrace I,X,Y,Z \rbrace \times \cdots \times \lbrace I,X,Y,Z \rbrace
次にスタビライザ群はパウリ群の部分群で $ -I $ を含まない可換なものとします。
スタビライザ形式は、あるスタビライザ群の要素となる演算子の固有値が+1である状態として状態を指定する方法です。
つまりスタビライザ $ S_i $ に対してスタビライザ状態 $ \vert S\rangle $ は $ S_i\vert S\rangle = \vert S\rangle $ となります。
具体例を見てみましょう。
スタビライザ群の例として $ S(2) = \lbrace I,X_1X_2,Z_1Z_2,-Y_1Y_2 \rbrace $ を考えます。
生成元は $ \lbrace X_1X_2,Z_1Z_2 \rbrace $ です。 $ S(2) $ の残りの要素である $ I, -Y_1Y_2 $ は生成元の積から作れます。
(X_1X_2)(X_1X_2) = I \\
(X_1X_2)(Z_1Z_2) = -Y_1Y_2
生成元は次のように可換であることを確認します。
X_iZ_i = -Z_iX_i \\
(X_1X_2)(Z_1Z_2) = X_1Z_1X_2Z_2 = (-Z_1X_1)(-Z_2X_2) = (Z_1Z_2)(X_1X_2)
スタビライザである生成元を作用させてもスタビライザ状態は変化しません。
X_1X_2(\vert00\rangle+\vert11\rangle)/\sqrt{2} = (\vert00\rangle+\vert11\rangle)/\sqrt{2} \\
Z_1Z_2(\vert00\rangle+\vert11\rangle)/\sqrt{2} = (\vert00\rangle+\vert11\rangle)/\sqrt{2}
クリフォード演算子
論理量子ゲートとしても使えるクリフォード演算子を導入します。HゲートとCNOTゲートがクリフォード演算子であることを確認します。Tゲートがクリフォード演算子でないことも示します。
クリフォード演算子はあるスタビライザ状態を別のスタビライザ状態に移す操作のことです。
クリフォード演算子 $ U $ をスタビライザ $ S_i $ で書けるスタビライザ状態 $ \vert S\rangle $ に作用させます。
S_i\vert S\rangle = \vert S\rangle \\
\rightarrow US_iU^{\dagger}(U\vert S\rangle) = U\vert S\rangle
$ S_i \rightarrow US_iU^{\dagger} $ の変換操作であるとみなせます。
アダマール(H)ゲートがクリフォード演算子であることを確認します。
次の関係が成り立つので $ H $ は $ X \rightarrow Z $ のスタビライザ演算子の変換であるといえます。
X\vert+\rangle = \vert+\rangle \\
\rightarrow HXH^{\dagger}(H\vert+\rangle) = Z(H\vert+\rangle) = Z\vert0\rangle = \vert0\rangle
上の計算では $ H\vert+\rangle = \vert0\rangle $ を使っています。
つまり $ X \rightarrow HXH^{\dagger} = Z $ となっています。
同様にCNOTゲートがクリフォード演算子であることを確認します。
$ XI \rightarrow XX, IZ \rightarrow ZZ $ のスタビライザ演算子の変換になっています。
XI\vert+\rangle\vert0\rangle = \vert+\rangle\vert0\rangle \\
\rightarrow (CNOT)XI(CNOT)^{\dagger}(CNOT\vert+\rangle\vert0\rangle) \\ = XX(CNOT\vert+\rangle\vert0\rangle) \\
= XX\left(\frac{1}{\sqrt{2}}(\vert00\rangle+\vert11\rangle)\right) = \frac{1}{\sqrt{2}}(\vert00\rangle+\vert11\rangle)
IZ\vert+\rangle\vert0\rangle = \vert+\rangle\vert0\rangle \\
\rightarrow (CNOT)IZ(CNOT)^{\dagger}(CNOT\vert+\rangle\vert0\rangle) \\ = ZZ(CNOT\vert+\rangle\vert0\rangle) \\
= ZZ\left(\frac{1}{\sqrt{2}}(\vert00\rangle+\vert11\rangle)\right) = \frac{1}{\sqrt{2}}(\vert00\rangle+\vert11\rangle)
上の計算では $ CNOT\vert+\rangle\vert0\rangle = \frac{1}{\sqrt{2}}(\vert00\rangle+\vert11\rangle) $ を使っています。
つまり次の関係が成り立っています。
XI \rightarrow (CNOT)XI(CNOT)^{\dagger} = XX \\
IZ \rightarrow (CNOT)IZ(CNOT)^{\dagger} = ZZ
Sゲートも同じくクリフォード演算子ですが、確認する過程は省略します。
Tゲートがクリフォード演算子でないことを示します。
T = \left[\begin{matrix} 0&0 \\ 0&e^{i\pi/4} \end{matrix}\right]
Tを使ってスタビライザ演算子Xを変換して、変換後もスタビライザ演算子になるかを調べます。
TXT^{\dagger} = \left[\begin{matrix} 0&0 \\ 0&e^{i\pi/4} \end{matrix}\right] \left[\begin{matrix} 0&1 \\ 1&0 \end{matrix}\right] \left[\begin{matrix} 0&0 \\ 0&e^{-i\pi/4} \end{matrix}\right] = \frac{1}{\sqrt{2}}(X+Y)
変換後はスタビライザ演算子にならないことがわかります。
したがってTゲートはクリフォード演算子ではありません。
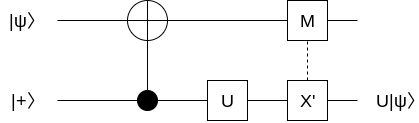
ゲートテレポーテーション
ゲートテレポーテーションは、ある量子ビットに作用させたゲート操作を別の量子ビットに作用させたように転送することです。ここでは次の回路で下側の量子ビットにかけたゲートを上側の量子ビットにかけたように操作できることを示します。
\lvert\psi\rangle := \alpha\lvert0\rangle + \beta\lvert1\rangle \\
\lvert+\rangle := \frac{\lvert0\rangle + \lvert1\rangle}{\sqrt{2}}
下をコントロール量子ビット、上をターゲット量子ビットとしてCNOTゲートを作用させます。
さらに下の量子ビットにユニタリゲートUを作用させると、この量子ビットの状態は次のようにかけます。
\frac{\lvert0\rangle U \left( \alpha\lvert0\rangle + \beta\lvert1\rangle \right) + \lvert1\rangle U \left( \beta\lvert0\rangle + \alpha\lvert1\rangle \right)}{\sqrt{2}}
上の量子ビットを測定したときに下の量子ビットの状態は次のようになります。
- 測定結果=0: $ U (\alpha\lvert0\rangle + \beta\lvert1\rangle) = U\lvert\psi\rangle $
- 測定結果=1: $ U (\beta\lvert0\rangle + \alpha\lvert1\rangle) = UX\lvert\psi\rangle $
上の量子ビットの測定結果が1のときだけ、さらに $ X' := UXU^{\dagger} $ を下の量子ビットに作用させると $ U\lvert\psi\rangle $ を得られます。
X'UX\lvert\psi\rangle = (UXU^{\dagger})UX\lvert\psi\rangle = U\lvert\psi\rangle
これで上の量子ビットの測定結果に関わらず、下の量子ビットに $ U\lvert\psi\rangle $ を得ることができました。実際には下の量子ビットに対してUゲートを作用させたにも関わらず、上の量子ビットに対してUゲートを作用させた結果を(下の量子ビットで)得ることができています。これがゲートテレポーテーションです。
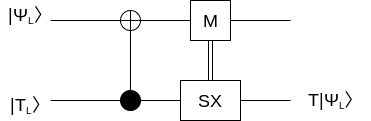
魔法状態蒸留
万能量子ゲートにはHゲート/Tゲート/CNOTゲートが必要です。しかし、Tゲートはクリフォード演算子に対応していないのでした。この問題を解決するために魔法状態蒸留を使います。この操作を施すことでTゲートと同様の操作を論理ビットに対して演算することができるようになります。
魔法状態 $ \vert T_L\rangle $ を用意してゲートテレポーテーションにかけると論理Tゲートを $ \vert\psi_L\rangle $ に作用させられます。
T = \left[\begin{matrix} 1&0 \\ 0&e^{i\pi/4} \end{matrix}\right], S = \left[\begin{matrix} 1&0 \\ 0&i \end{matrix}\right], X = \left[\begin{matrix} 0&1 \\ 1&0 \end{matrix}\right] \\
TXT^{\dagger} = e^{-i\pi/4} \left[\begin{matrix} 0&1 \\ i&0 \end{matrix}\right] = e^{-i\pi/4}SX
$ e^{-i\pi/4} $ がかかっていることを無視すれば SX ゲートと同じになります。
つまり実際に論理Tゲートを作用させなくとも、クリフォード演算子である論理S,Xゲートを使うことで論理Tゲートと同様の演算ができます。
ただし、魔法状態 $ \vert T_L\rangle $ をクリフォード演算子だけで用意することはできないので、これを作るのが魔法状態蒸留と呼ばれるゲートです。
魔法状態蒸留の実装は複数あります。これらの実装の詳細の説明は割愛しますが、多くの物理量子ビットとゲート操作を必要とするコストの高い演算になっています。
量子コンピュータを使って問題を解く際にはなるべくTゲートを使わないように実装を進める必要があります。
まとめ
本記事では誤り耐性万能量子コンピュータに関わる量子計算の基礎要素として量子誤り訂正、論理量子ビット、万能論理量子ゲートの概要を解説しました。
もし本記事には不足している知識を得たい意欲的な読者は参考文献やその他の資料を併せてご参照ください。
謝辞
私の知識や理解の不足によって間違っている箇所や誤解を招く表現を使っている場所があるかもしれません。
気づいたことがあればコメントをいただけるとうれしいです。
本記事が読者のみなさんの何かの役に立てば幸いです。