概要
私が開発を進めている終盤問題ジェネレーター(仮、以下ジェネレーターと略)の開発に関する記事です。
後述の通り、特にジェネレーターのPoCに焦点を当てています。
リバーシ検討図メーカーの話も入っているかもしれませんが、便宜上ジェネレーターの話として紹介いたします。
ITを本職とされている方々からすると気になる部分などあるかもしれませんが、素人の戯言でございますのでご容赦ください。
開発の目的
リバーシの終盤問題は既に複数の方が提供されています。
そういった問題集は良問が多い印象ですが、問題数に限りがあります。
無限に遊べる終盤問題集があればいいなと思い、開発を始めました。
環境選択
開発するときにまず、どの環境を対象にするかを考えました。
候補として主に下の3つがありました(表は私の知っている限りの話です)。
| 環境 | iOS | Android | Web |
|---|---|---|---|
| 言語 | Swift or Objective-C |
Java or Kotlin |
HTML5+CSS +JavaScript |
| iOS対応 | O | X | O |
| Android対応 | X | O | O |
| PC対応 | X | X | O |
| バイナリ実行 | O | O | X |
これに通信機能を付けると、バックエンドのコードも書く必要があります。
私は「PCでも遊べるようにしたい」「バックエンドでNode.jsを使いたい」といったことを考え、Webで開発することにしました。
PoC
準備段階
ジェネレーターで最も重要なのは生成エンジンの部分です。
本稿では「本当にそういったエンジンが作れるのか?」の検証(PoC)部分を中心に説明いたします。
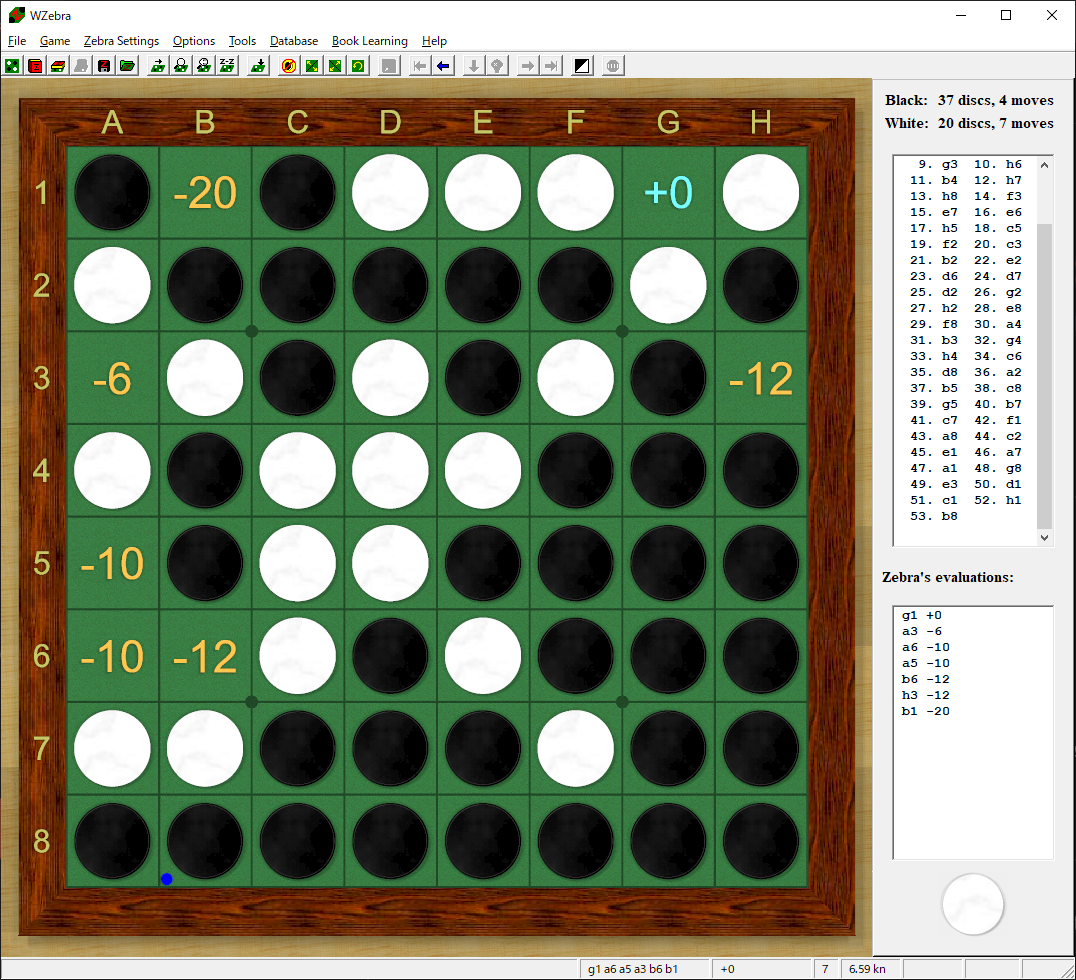
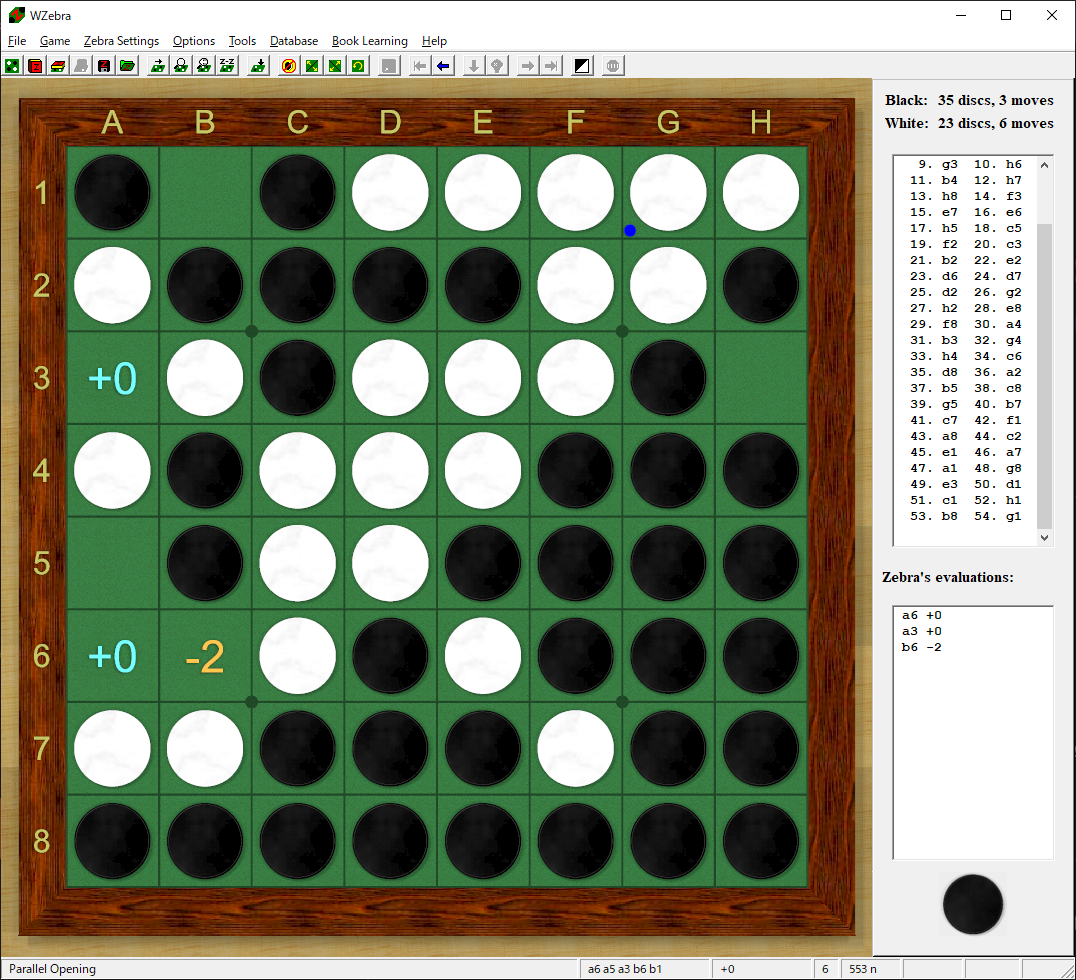
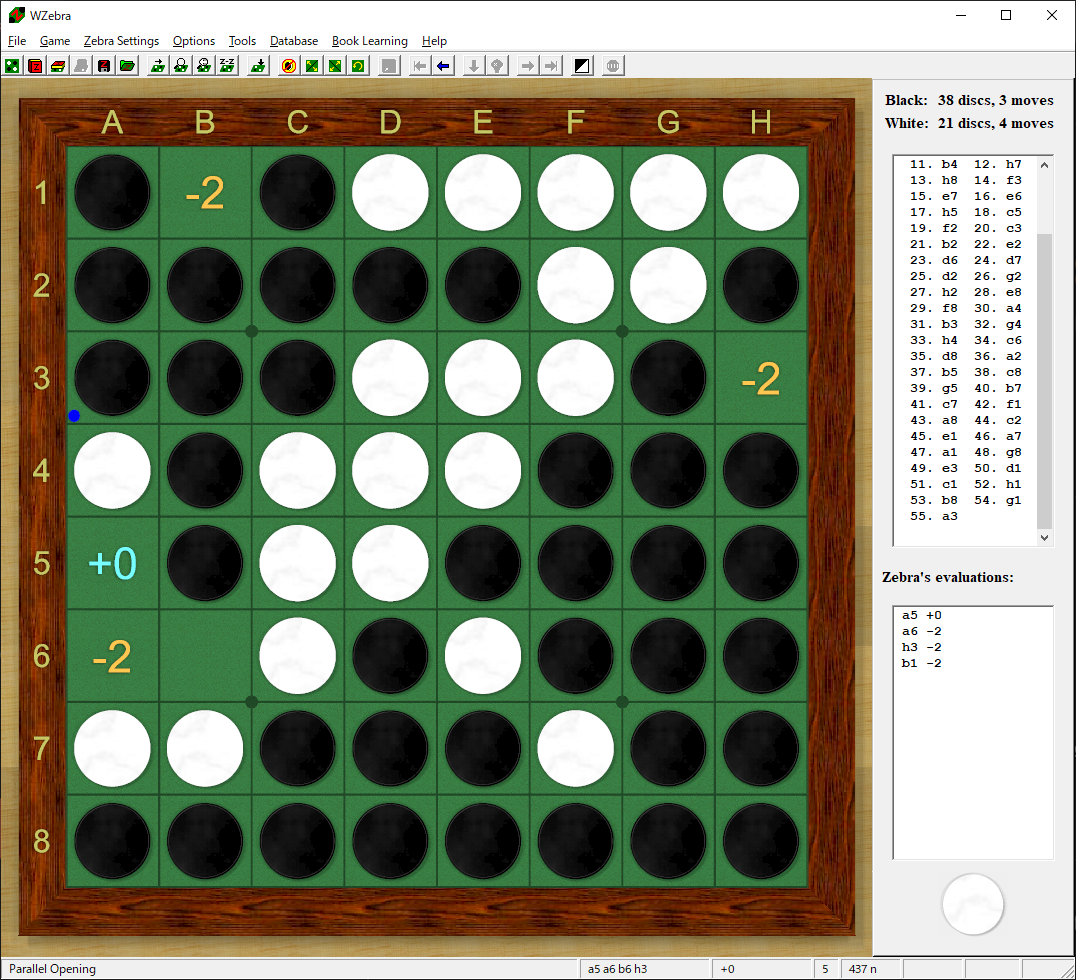
開発初期は棋譜を出力し、作成された問題をWZebraでチェックしていました。
(参考図)
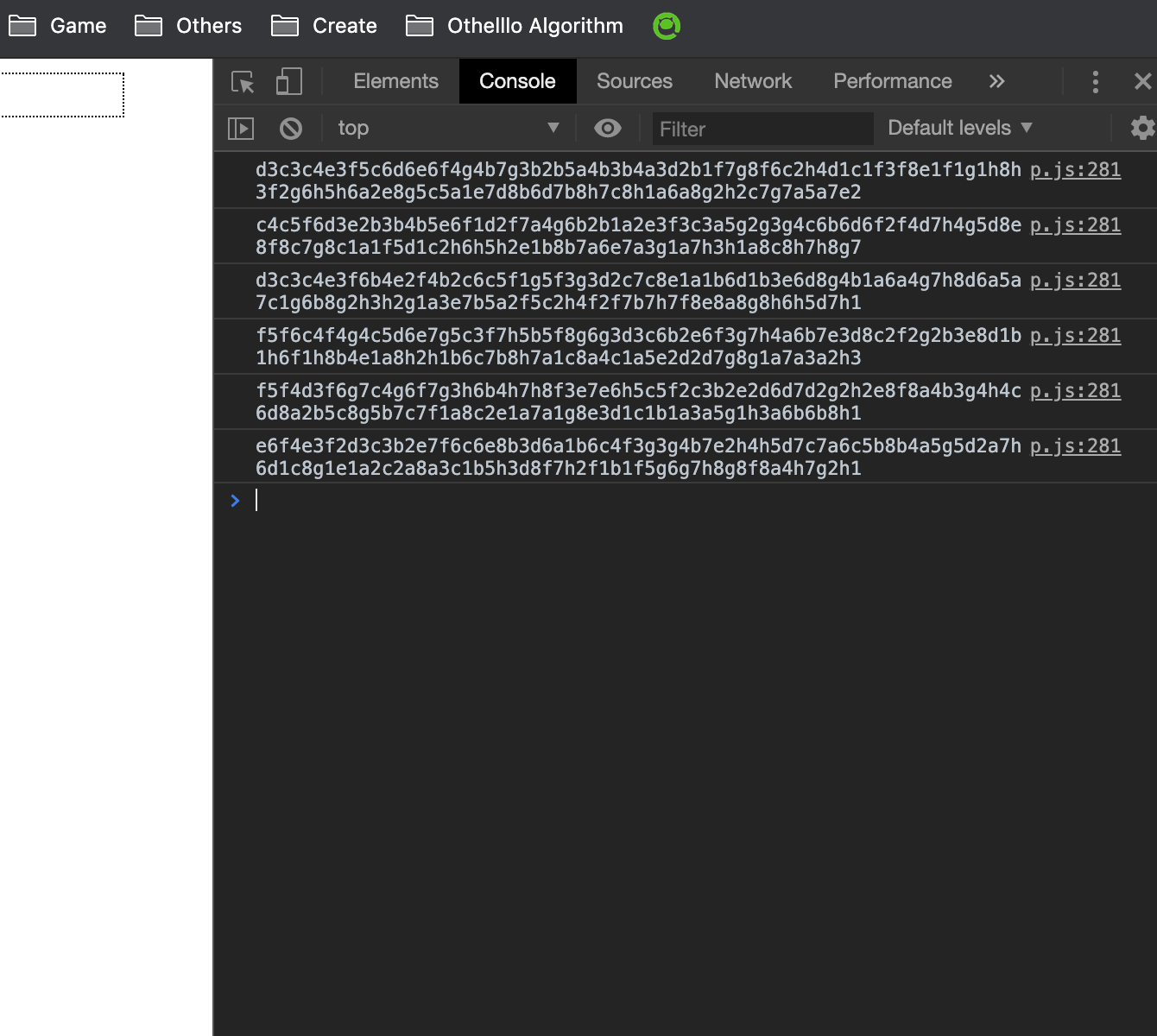
その後簡単な盤面表示関数を実装して、こちらでチェックするようにしました。
(X=黒石、O=白石)
PoC:Gen.1
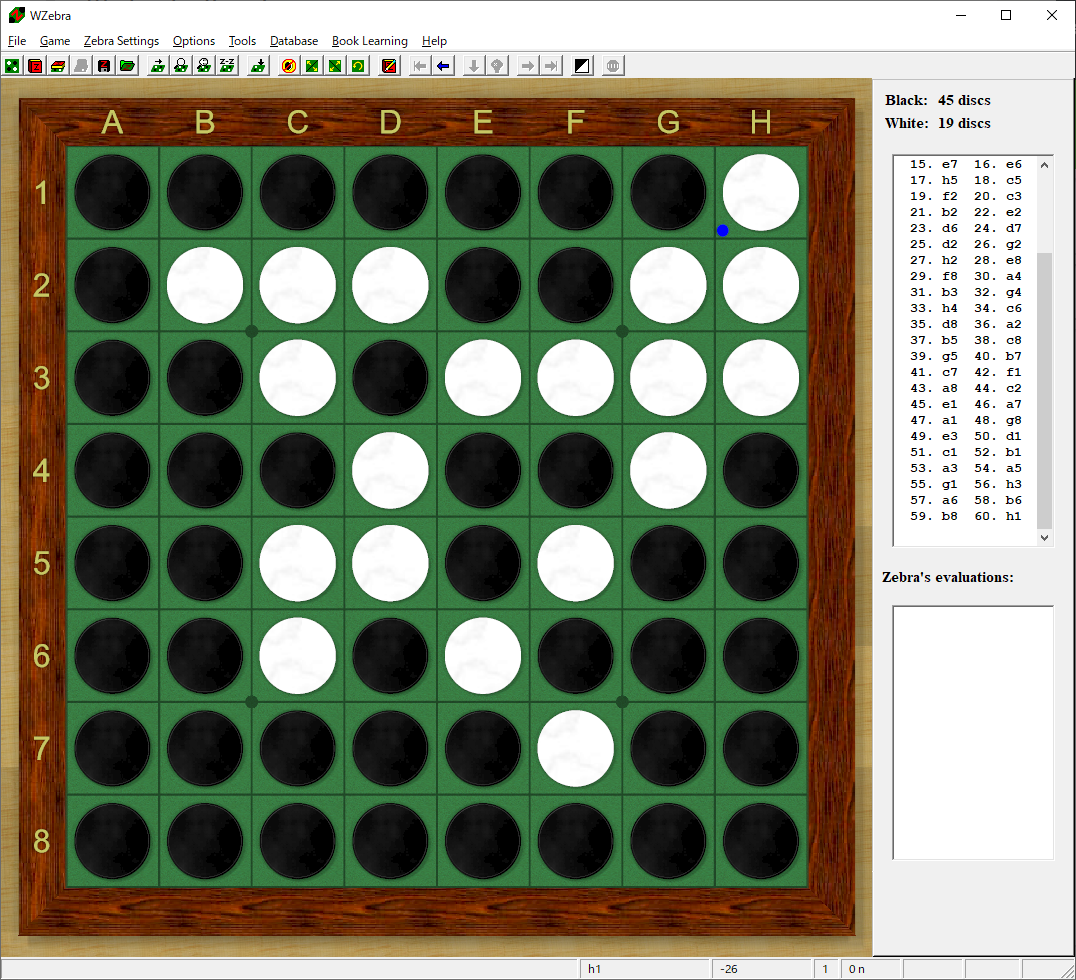
Gen.1(第一世代、以下同様)として、ランダムに着手するだけのエンジンを作りました。
(ただし全体を通して、ジェネレーター関数はdeterministicとなるようケアしました。)
f5f4d3f6g7c4g6f7g3h6b4h7h8f3e7e6h5c5f2c3b2e2d6d7d2g2h2e8f8a4b3g4h4c6d8a2b5c8g5b7c7f1a8c2e1a7a1g8e3d1c1b1a3a5g1h3a6b6b8h1
当然これでは、問題として通用する盤面は生成されません。
(下記解析例参照)
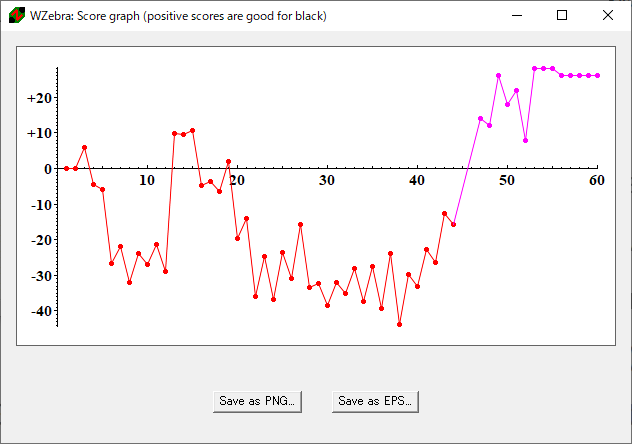
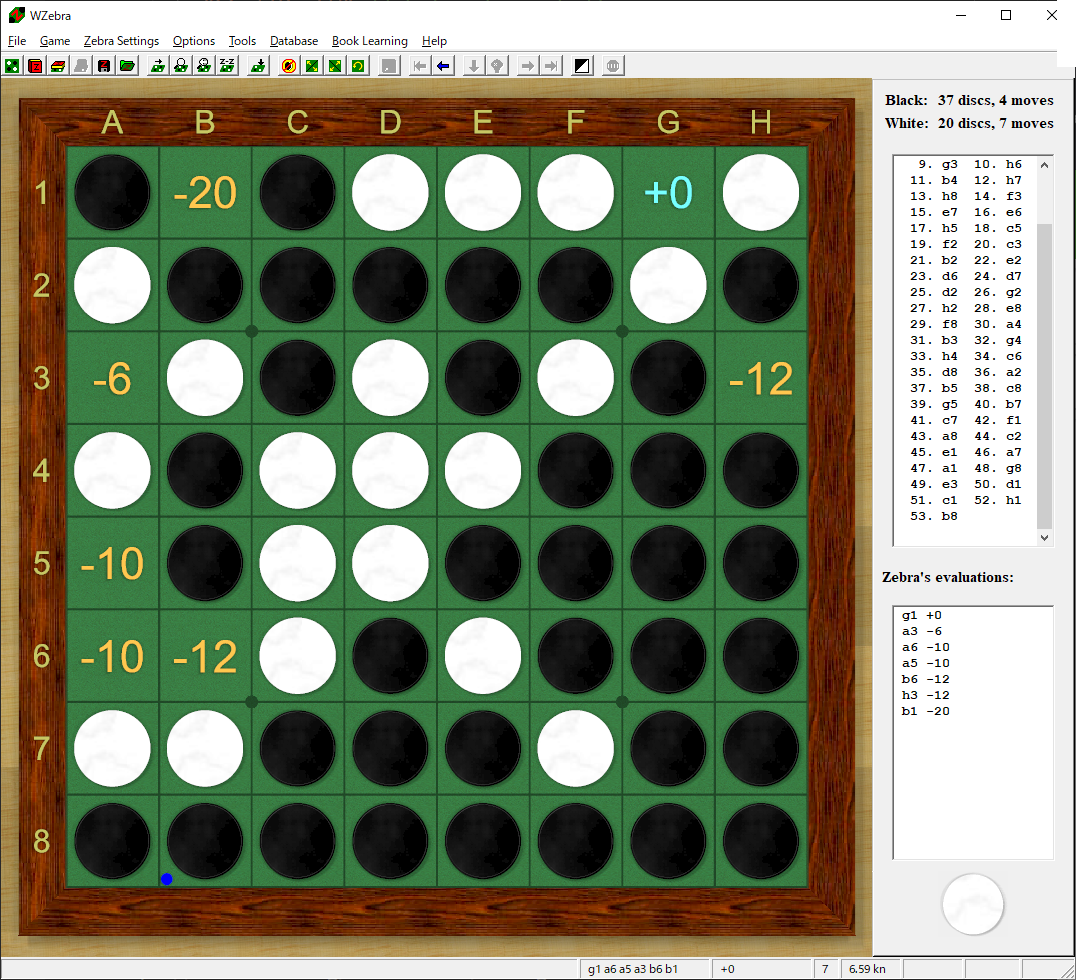
ただしこの、ランダムに着手するエンジンが全く使えないわけではありません。
様々試す中で、「ランダムな着手の一部を変更することで、互角に近い局面を生成すること」が可能であることが分かりました。
例えば棋譜例1ならば、52.h1 53.b8とすることでドロー局面が生じます。
PoC:Gen.2
Gen.1における試行の結果から、以下のような条件でエンジンを動作させることが有効と予想されます。
- ランダムな着手を途中で打ち切る
- 打ち切った局面から完全解析を実行
- 特定の評価値範囲内(例えば、黒+1~+10など)にある局面を抽出する
実際にこの条件で実行すると、以下の課題が見つかりました。
- 既に終局している局面が生成される。
- 最善進行の途中の局面が生成される。
- 不要なノードの探索に計算リソースが消費される
PoC:Gen.3
Gen.2の欠点を解消するため、追加で以下の制約を入れました。
- 連続して評価値Xの局面が生じる場合、評価値Xとなる空きマス数最多の局面のみを抽出する(課題1, 2対策)。
- 最低空きマス数を設定(課題3対策)
1について、例えば以下の3局面が検出された場合、1枚目の局面のみを抽出し、残りの局面は破棄することを意味します。
以上の対策の結果、以下のような棋譜を生成するエンジンが出来上がりました。
c4c5f6d3e2b3b4b5e6f1d2f7a4g6b2b1a2e3f3c3a5g2g3g4c6b6d6f2f4d7h4g5d8e8f8c7g8c1a1f5d1c2h6h5h2e1b8b7a6e7g1h1a7
c4c5f6d3e2b3b4b5e6f1d2f7a4g6b2b1a2e3f3c3a5g2g3g4c6b6d6f2f4d7h4g5d8e8f8c7g8c1a1f5d1c2h6h5h2e1b8b7a6e7g1g7c8
c4c5f6d3e2b3b4b5e6f1d2f7a4g6b2b1a2e3f3c3a5g2g3g4c6b6d6f2f4d7h4g5d8e8f8c7g8c1a1f5d1c2h6h5h2e1b8b7a6e7a3h3a7
ただし、生成された局面が「不自然」という課題がありました。
PoC:Gen.4
ジェネレーターをより実戦向きにするため、抽出される局面がより「自然」となるよう改良を実施しました。
解決に当たり、まず以下のような仮説を立てました。
- 人間から見て「不自然」な局面は、局面の見た目で判断されている。
- 局面の見た目は石の配置に依存する。
- 石の配置の「自然さ」を評価する静的評価関数を導入し、より評価値の高い局面を抽出することで、より「自然」な局面のみを生成するエンジンとなる
これを確認するため、まず以下の対策を行いました。
- 「自然さ」の評価関数導入
- 「自然さ」評価値上位の問題の抽出
評価方法の一例として、「空きマス同士が隣り合っているか?」を紹介いたします。
/*e0 and e1 : empty squares of upper/lower half.*/
function LFCountConnectedEmptySquares(e0,e1) {
var a = e0 << 8 & e0;
var b = e1 << 8 & e1 | e0 >>> 24 & e1;
var c = LFCountNumberOfDisks(a, b);
a = e0 << 7 & (e0 & 0x7f7f7f7f);
b = e1 << 7 & (e1 & 0x7f7f7f7f) | e0 >>> 25 & e1;
c += LFCountNumberOfDisks(a, b);
a = e0 << 9 & (e0 & 0xfefefefe);
b = e1 << 9 & (e1 & 0xfefefefe) | e0 >>> 23 & 0x000000fe & e1
c += LFCountNumberOfDisks(a, b);
a = e0 << 1 & (e0 & 0xfefefefe);
b = e1 << 1 & (e1 & 0xfefefefe);
return c + LFCountNumberOfDisks(a, b);
}
これはマスクしたbitboardをビットシフトしてAND演算することで、縦横斜めのいずれかの方向に空きマスがつながっているかを評価するものです。
あるマスから見て隣接マスは8か所ありますが、そのうち4か所と隣接しているかどうかを評価しています。
例えばa1マスから見てa2マスは下方向で隣接していますが、a2マスから見るとa1マスは上方向に隣接しています。
これらを重複してカウントする必要はありませんので、このうち「a1から見たa2の位置関係」のみをカウントしています。
このアルゴリズムは、bitboardでの着手アルゴリズムに着想を得て実装しています。
なおJavaScriptでは64bit整数が利用できないため、bitboardは32bit整数 x 2で表しています。
そのため空きマスビットはe0とe1の2つで表現しています。
この点についてはこちらの記事( https://qiita.com/rimol/items/9ed84a4fd4cbfdb83d71 )を参考にしました。
ある程度評価関数の実装とパラメーター設定ができたところで、一度アンケートを実施しました。
あなたはこの盤面が...
— AL4TH/あるふぉーす (@al4_th) December 15, 2019
あなたはこの盤面が...
— AL4TH/あるふぉーす (@al4_th) December 15, 2019
この時、同じ評価関数から得られた2つの局面について同時にアンケートをとりました。
結果、片方は「不自然」が多数、もう片方は「自然」が多数といったアンケート結果になりました。
このアンケート結果から、以下のように考えました。
- 同じアルゴリズムから「不自然」「自然」両方の局面を生成しうる。
- 評価関数の改良で「不自然」な局面を排除できるようになるのではないか?
PoC:Gen.5
Gen.4の考察から、色々と評価関数の調整を実施しました。
詳細は割愛しますが、以下のような局面(黒番)をコンスタントに生成するエンジンができました。
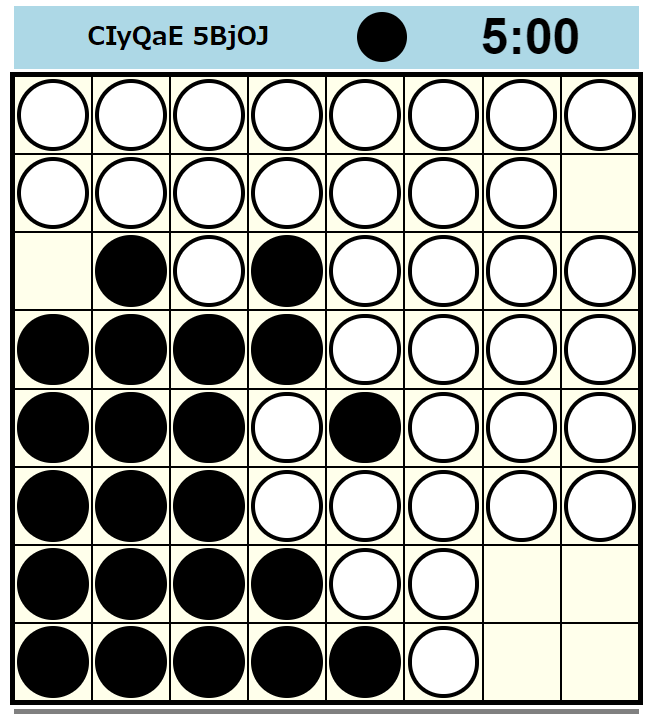
参考動画 : https://youtu.be/kfDp3Uc4LRI
まとめ
Gen.5である程度「自然」な局面を選択的に生成できるようになりましたので、PoCの目的を達しました。
エンジンは32bit整数 x 2をseedとして入力可能ですので、最大で64bit unsigned intの最大値=4294967295パターンの問題を生成可能です。
(必要な時はさらに追加可能。)
これからは、作成したエンジンを使って終盤問題アプリを作っていきたいと考えています。
最後に、オセロ Advent Calendarにお誘い頂いた@sensuikan1973さんに感謝申し上げます。
長らく駄文にお付き合いいただきありがとうございました。