こんにちは。akoamayと申します。butchi_yさんからのご紹介で寄稿させていただきます。
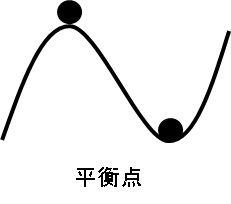
平衡点
今回はMathematicaを使って、n次元力学系
\dot{\bf x}={\bf f(\bf x)}, ({\bf x \in R^n})
の平衡点を鑑賞してみます。平衡点というのは
0={\bf f(\bf x)}
を満たすような x のことです。曲面上を転がるボールに例えると、ちょうどボールが静止する山の頂上と、底の位置に該当します。
ちなみに山頂にある点を「不安定」な、そして谷底にある平衡点を「安定」な平衡点といいます。この平衡点を観るために、まずは線形化という作業を行います。
線形化
力学系の、とある平衡点の位置を a とします。つまり、
0={\bf f(\bf a)}
を満たす a があるとします。
このとき、その力学系の x が a にとても近い時、テイラー展開を使って
\dot{\bf x}\fallingdotseq{\bf f(\bf a)}+{\bf f'(\bf a)(\bf x - \bf a)} + \cdot\cdot\cdot
と書いて、高次項を無視することができます。ここで、
{\bf J}={\bf f'(\bf a)=\frac{\partial {\bf f}}{\partial x} } |_{x=a}
{\bf x`=x-a}
とおくと、f(a)=0 であることから結局
\dot{\bf x’}={\bf J}{\bf x'}
となります。これは定数係数の線形微分方程式です。つまり、平衡点近傍の微小なズレ(x-a)に関する方程式は、元の式を線形化したものとなります。ちなみに J は元の力学系のヤコビ行列に平衡点の値を代入したものです。
固有値
もったいぶっていますがもうしばらくおつきあいを。
先ほど求めた式
\dot{\bf x}={\bf J}{\bf x} ,( {\bf x \in R^n})
は、もはや線形ですので、その一般解は基底関数
e^{\lambda_1t},e^{\lambda_2t},e^{\lambda_3t},\cdot\cdot\cdot,e^{\lambda_nt}
の重ねあわせで表現できます。で、
\lambda_1,\lambda_2,\lambda_3,\cdot\cdot\cdot,\lambda_n
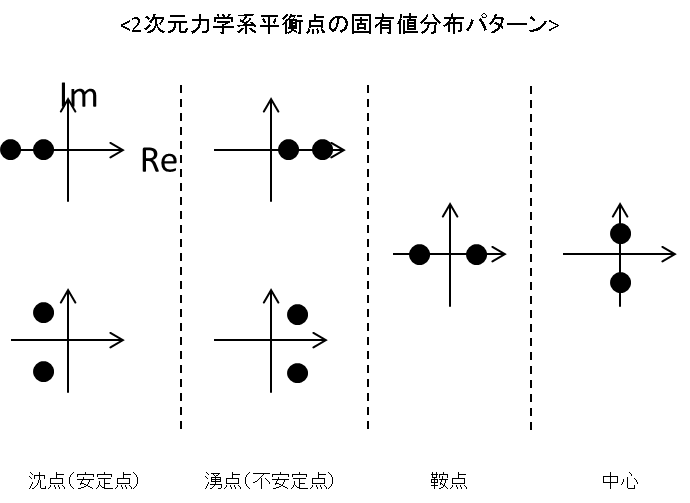
λ は J の固有値なので、これらの符号を見れば解のおおまかな挙動がわかります。例えば2次元系の場合はその符号の取りうるパターンは
- 2つとも負
- 2つとも正
- 正、負1つずつ
- 2つともゼロ
の4パターンになります。これらの平衡点には下のように名前がついています。
今回は、これらの位相的な性質の異なる4つの平衡点について、さらに固有値の実数、虚数の分布にも着目して分けた合計6つの平衡点を可視化してみます。
モデルの作成
上の6つの平衡点を観るために、それぞれの平衡点を持つような力学系を作ります。
行列Jの決定
今回は平衡点の位置を原点に置きます。そうすると、元の系を線形化した行列に原点の座標を代入した行列 J の固有値が上の分類のような配置になればいいわけです。少し手計算して、次のような6つの行列候補を求めてみました。
J_1=
\left(
\begin{array}{cc}
3 & 1 \\
-5 & -1 \\
\end{array}
\right),
J_2=
\left(
\begin{array}{cc}
-3 & 1 \\
-5 & 1 \\
\end{array}
\right),
J_3=
\left(
\begin{array}{cc}
1 & 0 \\
0 & 2 \\
\end{array}
\right),
J_4=
\left(
\begin{array}{cc}
-1 & 0 \\
0 & -2 \\
\end{array}
\right),
J_5=
\left(
\begin{array}{cc}
1 & 0 \\
0 & -1 \\
\end{array}
\right),
J_6=
\left(
\begin{array}{cc}
0 & -1 \\
1 & 0 \\
\end{array}
\right),
念のため、これらの行列の固有値分布が上の分類の通りになっているか確認してみましょう。ここでようやくMathematicaの登場です。
行列の固有値は
Eigenvalus[{{3,1},{-5,-1}}]
によって求めることができます。6つの行列全てを確認すると、
固有値の符号と実部、虚部の分布がちゃんと上の表の通りになっていますね。これで6つの行列Jが求まりました。
微分方程式をもとめる
行列Jが求まったので、ここから元の力学系の微分方程式をつくります。これは簡単です。Jはもとの式を微分して原点の値を代入したものですので、単純に積分すればOKです。
それぞれ下の通りになります。
A_1=
\left(
\begin{array}{cc}
3x & y \\
-5x & -y \\
\end{array}
\right),
A_2=
\left(
\begin{array}{cc}
-3x & y \\
-5x & y \\
\end{array}
\right),
A_3=
\left(
\begin{array}{cc}
x & 0 \\
0 & 2y \\
\end{array}
\right),
A_4=
\left(
\begin{array}{cc}
-1x & 0 \\
0 & -2y \\
\end{array}
\right),
A_5=
\left(
\begin{array}{cc}
x & 0 \\
0 & -y \\
\end{array}
\right),
A_6=
\left(
\begin{array}{cc}
0 & -y \\
x & 0 \\
\end{array}
\right),
これを用いて求めたい力学系は
\dot{\bf x}={\bf A_k\bf x}, (k=1,2,3,4,5,6)
\bf x=\left(
\begin{array}{c}
x\\
y\\
\end{array}
\right)
となります。
力学系を解いて平衡点を観る
これで準備が整いました。
求めた6つの力学系が生み出す平衡点付近の挙動を、Mathematicaを使って可視化してみます。
それには微分方程式の解を数値計算で近似する NDSolve を利用します。NDSolveは(恐らくルンゲクッタ法で)与えた微分方程式の積分をしてくれます。
まずは先にこちらをご覧ください。
これは上でもとめた力学系の平衡点を 美的に 可視化するコマンドです。
data = {};
Do[
x0 = RandomReal[{-10, 10}];
y0 = RandomReal[{-10, 10}];
sol = NDSolve[{x'[t] == 3x[t]+y[t],
y'[t] == -5x[t]-y[t], x[0] == x0, y[0] == y0}, {x,
y}, {t, 0, 10}];
data = Append[data,
ParametricPlot[Evaluate[{x[t], y[t]} /. sol], {t, 0, 10},
AspectRatio -> 1, PlotRange -> {{-10, 10}, {-10, 10}},
ColorFunction ->
Function[{x, y, t}, ColorData["DeepSeaColors"][t]],
BaseStyle -> Directive[Opacity[0.1]],
PlotStyle -> {Thickness[0.001]}, Axes -> False]
], {n, 1, 5000}];
Show[data]
何をやっているかというと、与えた微分方程式の時間発展をt=0~10まで求め、その結果得られる流線の軌跡を、薄い色で描画しています。そして、この処理を何度も何度も(上の例では5000回!)初期値をランダムに変えながら行って重ね描きをしているのです。ミソは「薄く細い線」で何度も重ね描きをすることです。こうすることで綺麗な図が得られます。
このコマンドをMathematicaに入力します。
当然、NDSolve内に入力する式は上で求めた6つの微分方程式です。具体的にはうえのA1であれば、
x'[t] == 3x[t]+y[t], y'[t] == -5x[t]-y[t]
となります。
これらをそれぞれ実行すると、結果として得られる出力は、下のようになります。(結果を得るのに数分かかるのでご注意ください。)
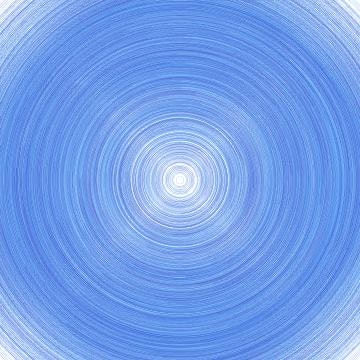
x'[t] == -y[t], y'[t] == x[t]
これは「中心」です。
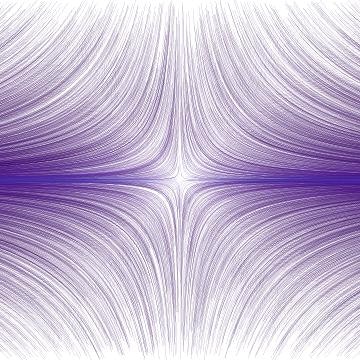
x'[t] == x[t], y'[t] == -y[t]
これはみんな大好き「鞍点」ですね。
x'[t] == x[t], y'[t] == 2*y[t]
これは「不安定節」といいます。
x'[t] == -x[t], y'[t] == -2*y[t]
これは「安定節」です。
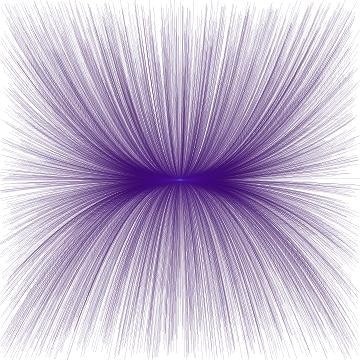
x'[t] == 3x[t]+y[t], y'[t] == -5*x[t]-y[t]
これは「不安定結節点」です。
x'[t] == -3x[t]+y[t], y'[t] == -5*x[t]+y[t]
これは「安定結節点」です。
うーんなんとも味わい深いではありませんか。Mathematicaを使うとこのような図が得られます。
まとめ
異なる種類の平衡点を持つ2次元力学系をいくつか作り、その解軌跡をNDSolveで求め、美的に可視化しました。
ちなみに、n次元力学系の位相的な性質はn+1個存在します。nが3の時は3Dで可視化すればよいのですが、それ以上の次元の時には単純に可視化できません。
4次元や5次元のときの平衡点を、いかにその特徴を崩さないで可視化するかという問題にも関心があるので、これもいつかMathematicaを使って取り組んでみたいと思います。