1.6 情報理論#
情報理論の分野から、確率論などについて考える
パターン認識や機械学習に必要ないくつかの概念を学習する
情報量##
情報量 $h(x)$
離散確率変数xに対して
「ある特定の値を観測したことで、どれだけ情報を受け取れるか」
1. $h(x)はp(x)に対し単調減少$
∵ p(x)が小さい → 情報量大
p(x)が大きい → 情報量小
2. $p(x,y) = p(x)p(y)に対し、h(x,y) = h(x) + h(y)$
∵ 2つの事象x,yが独立の時、
両方を観測した情報量=x,yそれぞれの情報量の和
∴ $h(x) = -log(p(x))$ (∵ 1.、2.)
* 0 ≦ p(x) ≦ 1 より、 0 ≦ h(x)
* 単位は底が2の場合ビット、eの場合ナット
エントロピー##
一度の事象で送れる情報量の期待値
$H[x]= -Σp(x)log(p(x))$
ノイズなし符号化定理:エントロピーと最短符号長の関係
例
箱への入れ方の総数は
N個の物体をどの順番で入れるかは N! 通り
i番目の箱の中ではni!通りの順番が存在する
∴ $W = \frac{N!}{Πni!}$
このWを多重度と呼ぶ
ミクロ状態:箱の中の物体の特定の状態
マクロ状態:比ni/Nで表される物体の占有数の分布
*多重度Wはマクロ状態の重みともいう
離散変数でのエントロピー###
$H[x]= -Σp(x)log(p(x))$
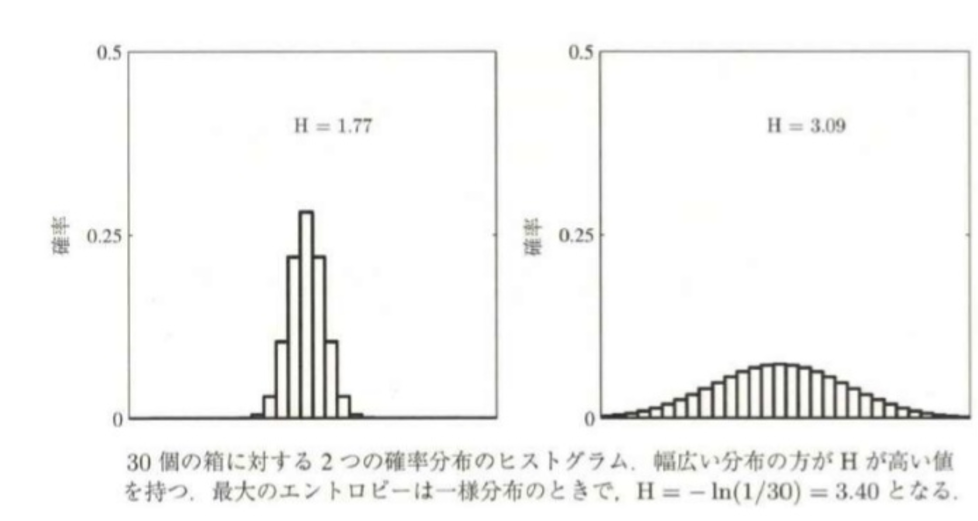
・エントロピー低:一部で鋭いピークをもつ時
・エントロピー高:値が広範囲に渡っている時
・エントロピー最小:ある一つの値がp=1で、他ではp=0となる時
・エントロピー最大:全てが等確率に起こる一様分布の時
↓
連続関数でのエントロピーはどうか
微分エントロピー##
連続変数xでの確率密度分布p(x)について考える
・xを等間隔の区間$Δx$に分ける ∵極限$(Δx→0)$をとるため
・平均値の定理より、
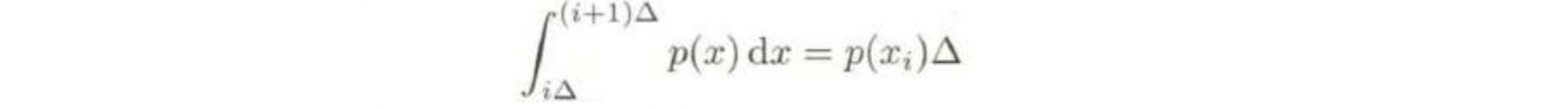
を満たす$x_i$が存在する。
・$x_i$を観測する確率は、$p(x_i)Δ$
・離散変数のエントロピーから
$H[x]= -Σp(x)ln(p(x))$
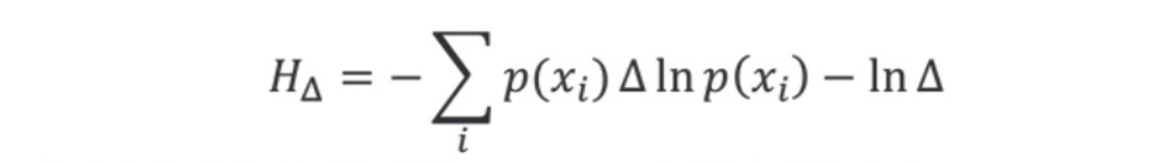
・$-InΔを無視してΔ→0の極限をとる$
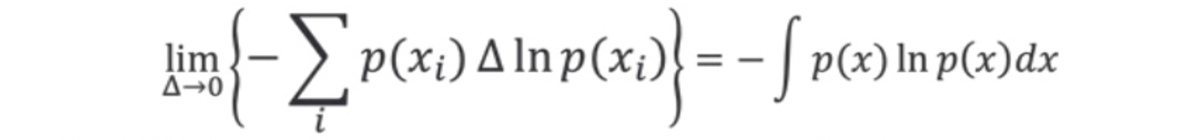
これを微分エントロピーという
微分エントロピーの最大化###
平均がμ、分散が$σ^2$となる分布の中で、エントロピーが最大になる分布
規格化制約: $\int p(x)dx = 1$
1次モーメント:$\int xp(x)dx = μ$
2次モーメント:$\int(x-μ)^2p(x)dx = σ^2$
これらの制約のもとで、ラグランジュ乗数法を用いて微分エントロピーを最大化する
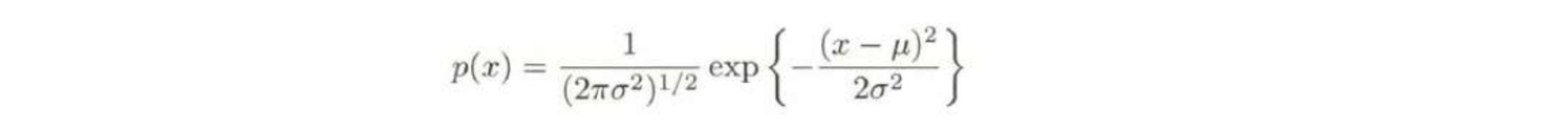
このp(x)のもとでHをもとめると
$H[x]=\frac{1}{2}[1+ln(2πσ^2)]$
条件付きエントロピー###
xのある値$x_i$が決まったあとで、yの値を特定するのに必要な情報量は$In p(y|x_i)$
∴条件付きエントロピーは
確率変数:
$H[x]=\sum_i p(x_i)H[y|x_i]=\sum_i p(x_i) \sum_j p(y_j|x_i)ln p(y_j|x_i)=\sum_i \sum_j p(x_i,y_i)ln p(y_j|x_i)$
連続変数:
$H[x]=\int\int p(x,y)ln p(y|x)dydx$
条件付きエントロピーと乗法定理から####
$H[x,y]=H[x|y]+H[x]$
1.6.1 相対エントロピーと相互情報量#
→情報理論の概念をパターン認識と関係付ける
相対エントロピー(KLダイバージェンス)##
未知の分布p(x)を近似的にq(x)でモデル化する
xの値を特定するのに必要な追加情報の平均は、
$KL(p||q)=-\int p(x) ln q(x)dx - (-\int p(x) ln p(x)dx)=-\int p(x)ln\frac {q(x)}{p(x)}dx$
これを$p(x)とq(x)$の相対エントロピー(KLダイバージェンス)という
KLダイバージェンスの性質###
・$KL(p||q)≠KL(q||p)$
・$KL(p||q)\geq 0$ $(等号成立は p(x)=q(x))$
イェンセンの不等式###
凸関数####
関数f(x)で、全ての弦が関数上か関数より上にある関数
弦の両端のみ弦が関数上に乗っている時、真に凸という

等号成立が$λ=0,1$のみの時、真に凸
この時、二回微分が常に正
イェンセンの不等式####
$f(λa+(1-λ)b)\leq λf(a)+(1-λ)f(b)$
より数学的帰納法から、
$f(\sum_{i=1}^{M}λ_ix_i)\leq $
$\sum_{i=1}^{M} λ_i f(xi)$
これをイェンセンの不等式という
相互情報量###
2つの変数集合x,yの同時分布p(x,y)に対し
・x,yが独立の場合、$p(x,y)=p(x)p(y)$
・x,yが独立でない場合、$KL(p(x,y)||p(x)p(y))$を利用する
$I[x,y]≡KL(p(x,y)||p(x)p(y))=-\int\int p(x,y)ln(\frac{p(x)p(y)}{p(x,y)})dxdy$
この$I[x,y]$を$x,y$間の相互情報量と呼ぶ
KLダイバージェンスより、
$I[x,y]=H[x]-H[x|y]=H[y]-H[y|x]$
であり、yの値を知ることによって、xに関する不確実性がどれだけ減少するかを表している