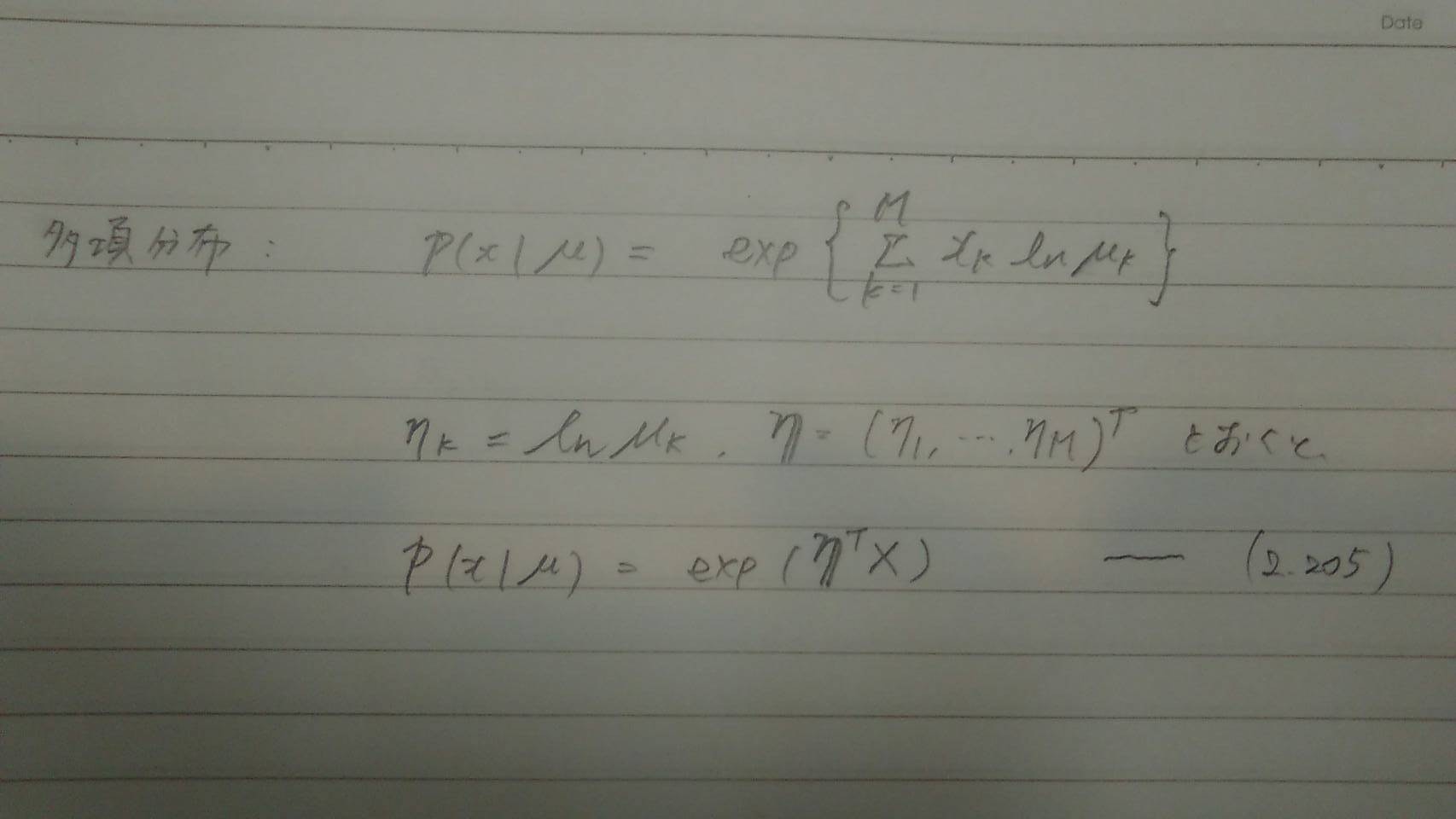指数型分布族#
$p(x|η)=h(x)g(η)exp(η^Tu(x))$ ・・・(2.194)
$η$:分布の自然パラメータ
$x$:ベクトル/スカラー・離散/連続
$u(x)$:xの任意の関数
$g(η)$:正規化係数 (2.195)
ベルヌーイ分布##
(2.194)と比較して、
$u(x)=x$
$h(x)=1$
$g(η)=σ(-η)$
とできるのでベルヌーイ分布は指数型分布族.
多項分布##
(2.194)と比較して、
$u(x)=x$
$h(x)=1$
$g(η)=1$
とできる.
ただし、$\sum_{k=1}^Mμ_k=1$
より、パラメータ $μ_k$のうちM-1個の値が与えられると残りのパラメータは決定するため、
$η_k$は独立ではない。
$μ_M$ を $μ_1~μ_{M-1}$で表す。

(2.212)を得る。
これを$μ_k$について解く。

(2.213)を得る。これをソフトマックス関数、正規化指数関数と呼ぶ。
このもとで、
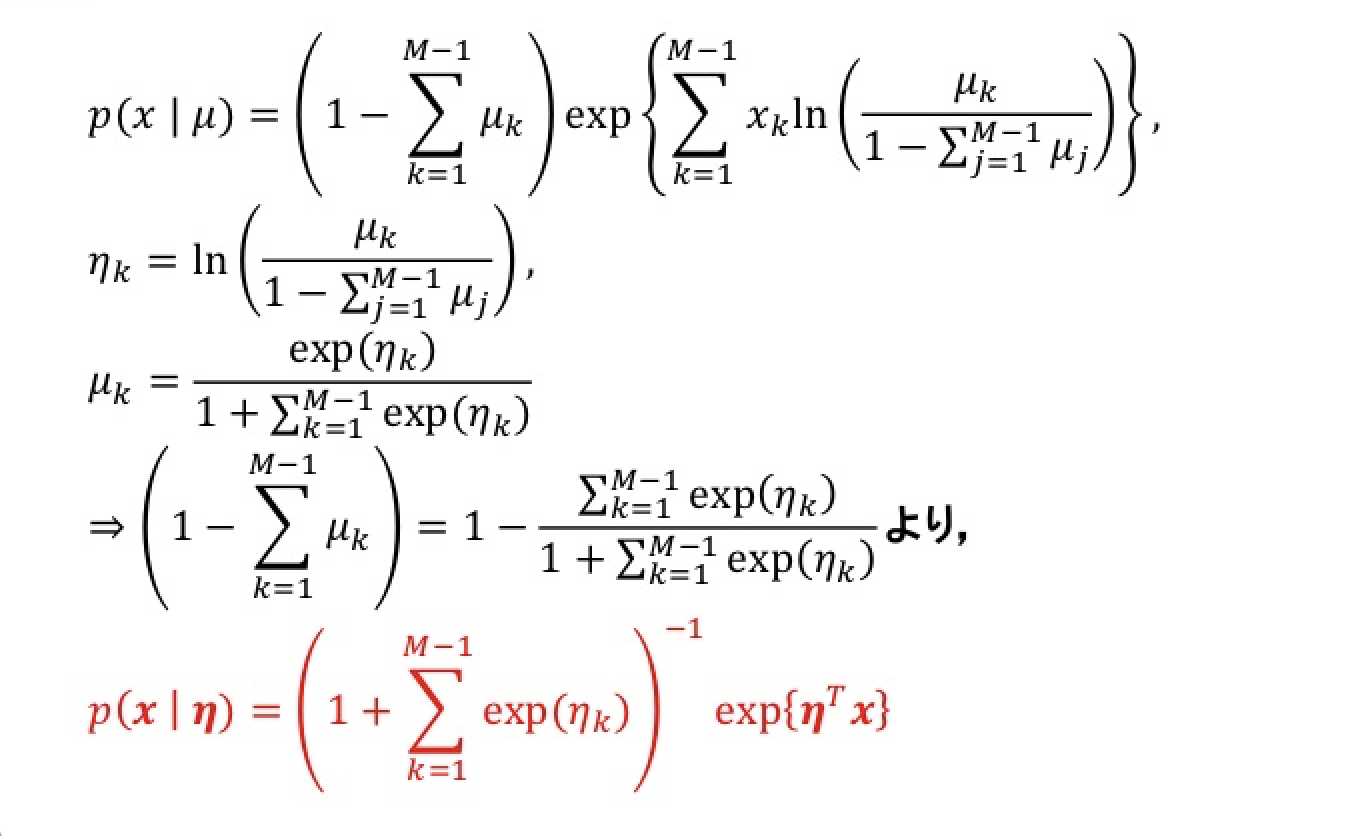
より多項分布は(2.214)の形をとる。
(2.194)と比較して、
$u(x)=x$
$h(x)=1$
$g(η)=(1+\sum_{k=1}^{M-1}exp(η_k))^1$
とでき、指数型分布族の標準形になっている。
ガウス分布##
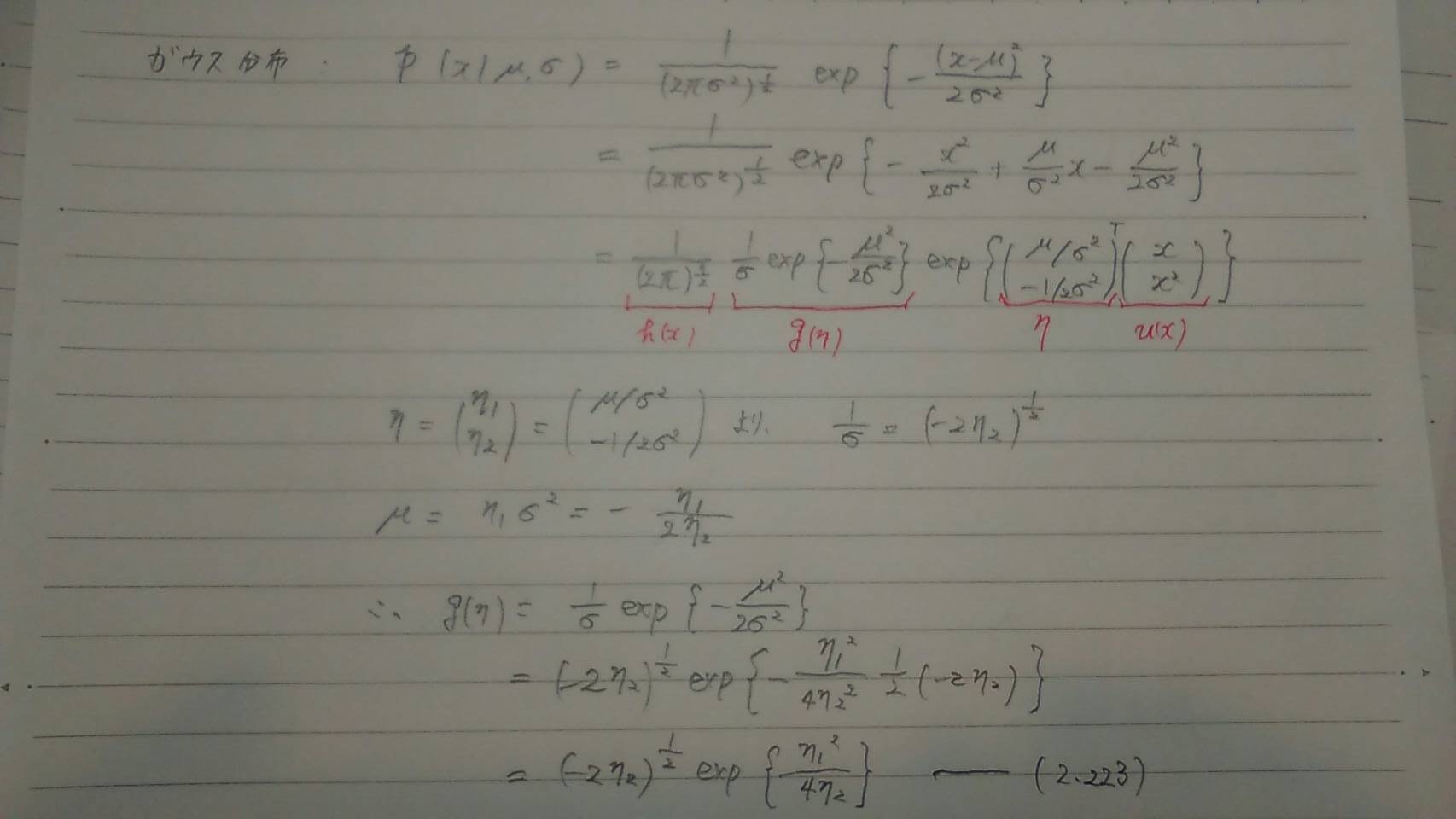
よって(2.220)~(2.223)が得られ、ガウス分布は指数型分布族.
ηを最尤推定##
正規化条件(2.195)の両辺の勾配を求める。→(2.224)
(2.224)の各項を(2.195)で割ると(2.225)が得られる。
$Δln g(η)=\frac{Δg(η)}{g(η)}$ より、
$E[u(x)]=-Δlng(η)$
○ $u(x)$の期待値は$g(η)$のみに依存することがわかるので、指数型分布族の分布を正規化できれば、その分布のモーメントは単に微分すれば求められる。

$η_{ML}$は $\sum u(x)$のみに依存している。
十分統計量###
$\sum_nu(x_n)をp(x|η)$の十分統計量と呼ぶ
○ データ集合全体を保持する必要はなく、この十分統計量の値だけ保持していれば良い.
(例)
ベルヌーイ分布
$u(x)=x$より、データ点{$x_n$}の総和を保持すれば良い.
ガウス分布
$u(x)=(x,x^2)^T$より、{$x_n$}の総和、{$x_n^2$}の総和を保持すれば良い.
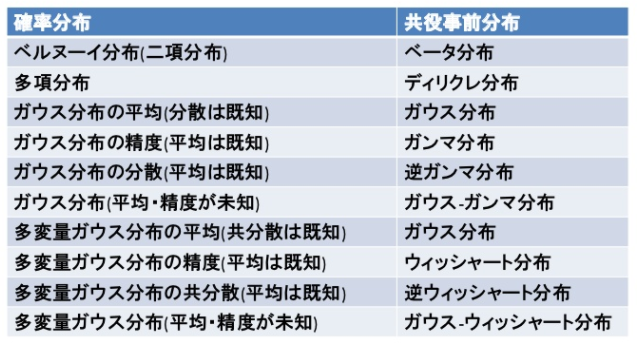
共役事前分布##
尤度関数と掛けて事後分布を求めると、その関数形が同じになるような事前分布。
指数型分布族の任意の分布について、共役事前分布は
$p(η|χ,ν)=f(χ,ν)g(η)^νexp(νη^Tχ)$・・・(2.229) とかける。
$f(χ,ν)$は正規化係数.
$g(η)$は(2.195)と同じ.
確かに、事前分布(2.229)に尤度関数(2.227)をかけると(2.230)が得られる。
これは(2.229)と同じ関数形なので、この事後分布は共役である。
共役事前分布の例####
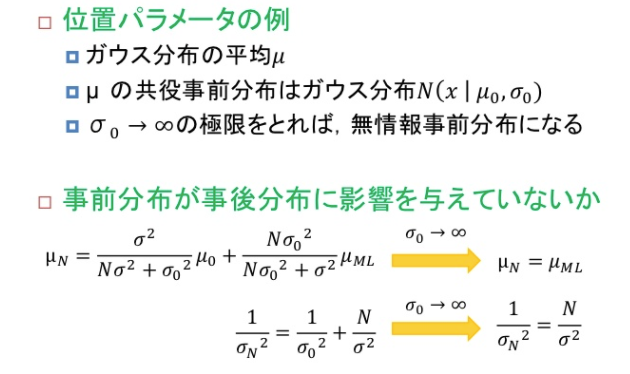
無情報事前分布##
事前分布に対する知見がないとき、事後分布に用いる事前分布の影響が少なくなるような事前分布.
無情報事前分布の例####
①平行移動不変性を持つ事前分布
$p(x|μ)=f(x-μ)$
μ:位置パラメータ
これはxを定数分移動しても同じ形式が保たれる=平行移動不変性
(特徴)
$p(σ)=const$
②尺度不変性を持つ事前分布
$p(x|σ)=\frac{1}{σ}f(\frac{x}{σ})$
σ:尺度パラメータ
これはxを定数倍拡大縮小しても同じ形式が保たれる=尺度不変性
(特徴)
$p(σ)∽\frac{1}{σ}$ ・・・(1)
変則事前分布になる ・・・(2)
$p(lnσ)=const$ ・・・(3)
(1) $p(σ)=\frac{a}{σ}$(aは定数)を(2.)に代入
(2) 範囲は0以上→積分が発散するので規格化不可
(3) $p(σ)=\frac{a}{σ}$(aは定数)と置く。
$t=lnσ$と置くと、
$\frac{dt}{dσ}=\frac{1}{σ}$ ⇔ $\frac{dσ}{dt}=σ$
より、$p(lnσ)=p(t)=p(σ)\frac{dσ}{dt}=\frac{a}{σ}σ=a$