NBA(アメリカバスケットボールリーグ)におけるレイカーズの優勝確率
はじめに
私は学生の頃バスケットボール部に所属しており、本や雑誌から戦術を、ポスターを見てプロ選手のフォームを真似してみたりとうまくなるために日々研究していました。
その中で一番参考にした選手が(故)コービー・ブライアントというNBA選手です。
NBAは1シーズン当たり、各チーム(全体30チーム)が通常82試合を行い、成績上位チームがプレーオフ(東西上位8チームずつが出場。トーナメント式で日本野球の日本シリーズに近い構造。後ほど解説します。)に進出し、全体の優勝を決めるというリーグとなってます。
彼はLos Angels Lakers(以降レイカーズ)というチームに所属してました。当時のリーグでは三連覇を達成しており、彼はその中でもシーズンMVP、ファイナルMVPを二度獲得という大スター選手でした。
そんな彼の所属していたレイカーズですが、昨年度はシーズン順位3位、プレーオフ1回戦敗退という残念な結果に終わり、オフシーズンを迎えました。現在レイカーズには八村塁選手が在籍しておりチームの主軸の一人です。日本人初のNBA優勝経験をしてもらうべく数字の世界からレイカーズを分析し、優勝への可能性、強化ポイントなどを見てみたいと思いました。
分析データ
kaggleよりデータセット 「NBADataBase」 1960年代から2022年までの全試合データ
NBAreference プレーオフ順位データ、レーカーズ試合、順位データ(サイト内操作にて表をエクセルファイルとしてダウンロード)
実行環境
パソコン:msi Modern-15-H-B13M
開発環境:vsCode
言語:Python
ライブラリ:Pandas, Matplotlib,xgboost,
分析の流れ
1.データのインポート
2.優勝チームのデータを抽出し試合の傾向やトレンドを把握、特徴量の選定
3.データの加工、前処理
4.モデル作成
5.作成したモデルにレイカーズのデータを入れて優勝確率を算出
6.平均数値を確認
7.昨年度優勝チームの優勝確率を算出
8.優勝チームとレイカーズの違いをグラフで確認し、優勝に必要な要素を洗い出す
9.分析の考察とまとめ
分析の過程に進む前にプレーオフのトーナメントルールと、
バスケットボールの試合データは英語表記なので、各単語を簡単に解説しておきます。
用語解説
home :ホーム 試合がホームで行われたこと
away :アウェイ 試合がアウェイで行われたこと
won :勝利 その試合に勝利したかを示す
fg :フィールドゴール すべてのエリアでの成功したシュート数
fg3 :フィールドゴール3 成功した3ポイントシュート数
ft :フリースロー フリースローによる得点
efg :イーフィールドゴール 3ポイントシュートの確率に重みづけしたシュート成功率
〇〇a :アテンプト シュートやフリースローの試投数(例:fga=FGアテンプト)
stl :スティール 相手のボールを奪うプレイ
blk :ブロック 相手のシュートを弾いて阻止するプレイ
ast :アシスト 味方の得点をアシストするパス
tov :ターンオーバー ミスや相手のスティールで攻撃権を失うこと
reb :リバウンド シュートミス後のボールを確保するプレイ
pf :パーソナルファウル ディフェンス・オフェンスのファウル総称
pts :ポイント 総得点
プレーオフについて
各(※1)カンファレンスの8チームが進出し、上位シードと下位シードと対戦します。7戦のうち4勝を先に挙げたチームがカンファレンス準決勝に進出する。上位シードチームにホームアドバンテージが与えられ、最初の2ゲームを含む4試合をホームでプレーできる。
1回戦の対戦振り分け
第1シード vs 第8シード
第2シード vs 第7シード
第3シード vs 第6シード
第4シード vs 第5シード
つまり、シーズンを上位でキープできれば有利な条件で戦うことができます。
※1 正式にはイースタンカンファレンス・ウェスタンカンファレンスといい、東西で15チームずつに分かれています。
又、第7,8シードはNBAのリーグルール上、純粋な順位だけではプレーオフ参加が決まりません。
上位6チームは無条件で参加できますが、7~10位のチームは残りの2枠をかけてプレーイン・トーナメントを行い参加枠を争います。
分析の過程
必要なライブラリのインポートとSQLiteファイルの読み込み
実行したコード
import sqlite3
import pandas as pd
import matplotlib.pyplot as plt
import xgboost as xgb
conn = sqlite3.connect('../nba_data.sqlite/nba.sqlite')
過去に優勝したチームの傾向、トレンドを知るためにチャンピオンのみを抽出します。
データにはどのチームが優勝したかの情報は入っていないため、プレーオフ最終戦の勝利チームをチャンピオンとして判定して抽出します。
2000年以降でデータを絞りましたが、2001年と2005年にデータの欠損が見られたため、2010年以降をデータ解析の対象とすることに決定しました。
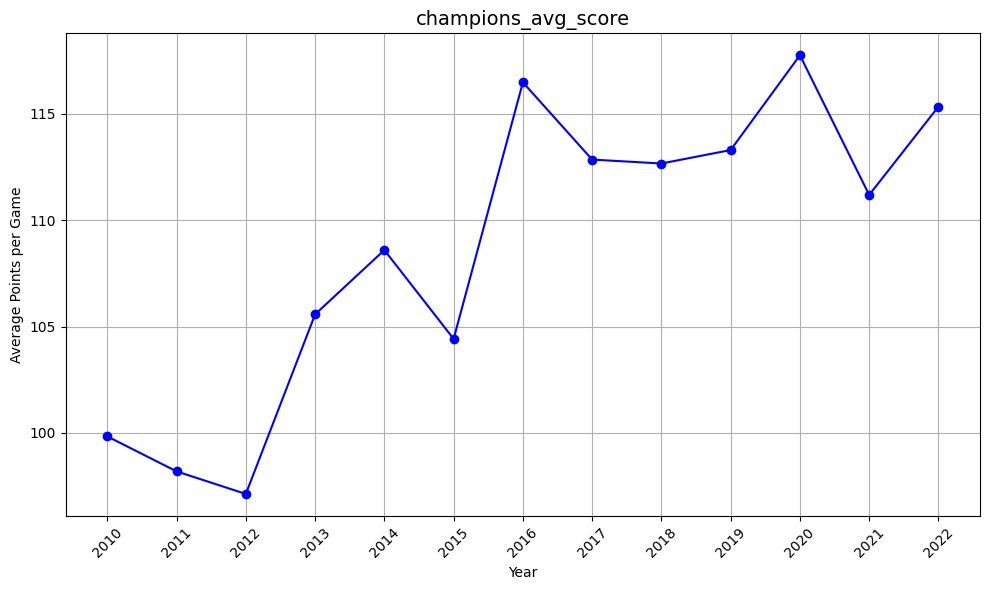
年々3ptシュート中心の戦術が増えてきているとのことなので、1試合ごとの平均得点を確認します。
実行したコード
# 優勝チームのシーズンごとの平均得点を出力
plt.figure(figsize=(10, 6))
plt.plot(champion_avg_stats['champion_year'], champion_avg_stats['avg_pts'], marker='o', linestyle='-', color='blue')
# グラフの装飾
plt.title('champions_avg_score', fontsize=14)
plt.xlabel('Year')
plt.ylabel('Average Points per Game')
plt.grid(True)
plt.xticks(champion_avg_stats['champion_year'], rotation=45)
plt.tight_layout()
# 表示
plt.show()
12年間の間で平均得点が10点上がっていることが分かりました。
明らかに攻撃のスタイルが変わってきていることがうかがえます。
次に、シュートの内容を検証するべく、2ptと3ptの比率をプロットします。
実行したコード
import matplotlib.pyplot as plt
# 2pt・3pt試投数の比較
plt.figure(figsize=(10, 6))
plt.plot(champion_avg_stats["champion_year"], champion_avg_stats["avg_2pa"], label="2PT Avg Attempts", marker="o")
plt.plot(champion_avg_stats["champion_year"], champion_avg_stats["avg_fg3a"], label="3PT Avg Attempts", marker="o")
plt.plot(champion_avg_stats["champion_year"], champion_avg_stats["avg_fga"], label="Avg Attempts", marker="o")
plt.title("Average FG Attempts per Game (2PT vs 3PT)")
plt.xlabel("Year")
plt.ylabel("Average Attempts per Game")
plt.legend()
plt.grid(True)
plt.show()
3ptシュートの試投回数が上昇傾向にあることが分かりました。
これにより、3ptを打つことが戦術として重要になってきていることが読み取れます。
また、全体のシュート試投回数も増加傾向にあるため、試合のオフェンステンポが上がってきていると予想されます。
※この期間に1試合の総試合時間は変更されていません
オフェンスが高い要素を持つことが想定されます。
データの作成
今回の対象となるデータは、2010年から2022年までの間の全チームの試合です。(1シーズンあたり82試合+プレーオフを12年分)
レギュラーシーズンとプレーオフが別のidで管理されているため、レギュラーシーズンとプレーオフを分けて抽出します。1試合ごとの平均を計算し、regular_dfとplayoff_dfを作成し、
それらを統合して、merged_stats(統合版)を作成します。
実行したコード
nba_game_df = pd.read_sql_query("SELECT * FROM game", conn)
# 空白除去して、レギュラーシーズンを抽出
nba_game_df['season_type'] = nba_game_df['season_type'].str.strip()
regular_df = nba_game_df[nba_game_df['season_type'] == 'Regular Season'].copy()
# season_id を int に変換
regular_df['season_id'] = regular_df['season_id'].astype(int)
regular_df['season_year'] = regular_df['season_id'] - 20000
regular_df = regular_df[regular_df['season_year'] >= 2010]
# 勝敗を数値に変換
regular_df['won_home'] = regular_df['wl_home'].map({'W': 1, 'L': 0})
regular_df['won_away'] = regular_df['wl_away'].map({'W': 1, 'L': 0})
# ホームチームのデータ抽出
home_stats = regular_df[[
'season_year', 'team_name_home', 'fg_pct_home', 'fg3_pct_home', 'ft_pct_home',
'reb_home', 'ast_home', 'stl_home', 'blk_home', 'tov_home', 'pts_home',
'won_home', 'fga_home', 'fg3a_home', 'fta_home', 'pf_home', 'pts_away'
]].copy()
home_stats = home_stats.rename(columns={
'team_name_home': 'team_name',
'fg_pct_home': 'fg_pct',
'fg3_pct_home': 'fg3_pct',
'ft_pct_home': 'ft_pct',
'reb_home': 'reb',
'ast_home': 'ast',
'stl_home': 'stl',
'blk_home': 'blk',
'tov_home': 'tov',
'pts_home': 'pts',
'won_home': 'won',
'fga_home': 'fga',
'fg3a_home': 'fg3a',
'fta_home': 'fta',
'pf_home': 'pf',
'pts_away': 'pts_against'
})
# アウェイチームのデータ抽出
away_stats = regular_df[[
'season_year', 'team_name_away', 'fg_pct_away', 'fg3_pct_away', 'ft_pct_away',
'reb_away', 'ast_away', 'stl_away', 'blk_away', 'tov_away', 'pts_away',
'won_away', 'fga_away', 'fg3a_away', 'fta_away', 'pf_away', 'pts_home'
]].copy()
away_stats = away_stats.rename(columns={
'team_name_away': 'team_name',
'fg_pct_away': 'fg_pct',
'fg3_pct_away': 'fg3_pct',
'ft_pct_away': 'ft_pct',
'reb_away': 'reb',
'ast_away': 'ast',
'stl_away': 'stl',
'blk_away': 'blk',
'tov_away': 'tov',
'pts_away': 'pts',
'won_away': 'won',
'fga_away': 'fga',
'fg3a_away': 'fg3a',
'fta_away': 'fta',
'pf_away': 'pf',
'pts_home': 'pts_against'
})
# ホームとアウェイのデータを縦に結合
team_stats = pd.concat([home_stats, away_stats], ignore_index=True)
# チームごと・シーズンごとの平均を計算
season_team_stats = team_stats.groupby(['season_year', 'team_name']).agg({
'fg_pct': 'mean',
'fg3_pct': 'mean',
'ft_pct': 'mean',
'reb': 'mean',
'ast': 'mean',
'stl': 'mean',
'blk': 'mean',
'tov': 'mean',
'pts': 'mean',
'pts_against': 'mean',
'won': 'mean',
'fga': 'mean',
'fg3a': 'mean',
'fta': 'mean',
'pf': 'mean'
}).reset_index()
# 2PT 試投数の追加(FGA - FG3A)
season_team_stats['avg_2pa'] = season_team_stats['fga'] - season_team_stats['fg3a']
#Four Factorsの導入
season_team_stats['efg_pct'] = season_team_stats['fg_pct'] + 0.5 * (season_team_stats['fg3a'] / season_team_stats['fga']) * season_team_stats['fg3_pct']
season_team_stats['tov_pct'] = season_team_stats['tov'] / (season_team_stats['fga'] + 0.44 * season_team_stats['fta'] + season_team_stats['tov'])
season_team_stats['ftr'] = season_team_stats['fta'] / season_team_stats['fga']
プレーオフも同様に作成します。
実行したコード
nba_game_df = pd.read_sql_query("SELECT * FROM game", conn)
conn.close()
# 空白除去してプレーオフのみ抽出
nba_game_df['season_type'] = nba_game_df['season_type'].str.strip()
playoffs_df = nba_game_df[nba_game_df['season_type'] == 'Playoffs'].copy()
# 型変換とフィルタ
playoffs_df['season_id'] = playoffs_df['season_id'].astype(int)
playoffs_df['season_year'] = playoffs_df['season_id'] - 40000
playoffs_df = playoffs_df[playoffs_df['season_year'] >= 2010]
# 勝敗を数値に変換
playoffs_df['won_home'] = playoffs_df['wl_home'].map({'W': 1, 'L': 0})
playoffs_df['won_away'] = playoffs_df['wl_away'].map({'W': 1, 'L': 0})
# ホームチームのデータ抽出
po_home_stats = playoffs_df[[
'season_year', 'team_name_home', 'fg_pct_home', 'fg3_pct_home', 'ft_pct_home',
'reb_home', 'ast_home', 'stl_home', 'blk_home', 'tov_home', 'pts_home',
'won_home', 'fga_home', 'fg3a_home', 'fta_home', 'pf_home', 'pts_away'
]].copy()
po_home_stats = po_home_stats.rename(columns={
'team_name_home': 'team_name',
'fg_pct_home': 'fg_pct',
'fg3_pct_home': 'fg3_pct',
'ft_pct_home': 'ft_pct',
'reb_home': 'reb',
'ast_home': 'ast',
'stl_home': 'stl',
'blk_home': 'blk',
'tov_home': 'tov',
'pts_home': 'pts',
'won_home': 'won',
'fga_home': 'fga',
'fg3a_home': 'fg3a',
'fta_home': 'fta',
'pf_home': 'pf',
'pts_away': 'pts_against'
})
# アウェイチームのデータ抽出
po_away_stats = playoffs_df[[
'season_year', 'team_name_away', 'fg_pct_away', 'fg3_pct_away', 'ft_pct_away',
'reb_away', 'ast_away', 'stl_away', 'blk_away', 'tov_away', 'pts_away',
'won_away', 'fga_away', 'fg3a_away', 'fta_away', 'pf_away', 'pts_home'
]].copy()
po_away_stats = po_away_stats.rename(columns={
'team_name_away': 'team_name',
'fg_pct_away': 'fg_pct',
'fg3_pct_away': 'fg3_pct',
'ft_pct_away': 'ft_pct',
'reb_away': 'reb',
'ast_away': 'ast',
'stl_away': 'stl',
'blk_away': 'blk',
'tov_away': 'tov',
'pts_away': 'pts',
'won_away': 'won',
'fga_away': 'fga',
'fg3a_away': 'fg3a',
'fta_away': 'fta',
'pf_away': 'pf',
'pts_home': 'pts_against'
})
# ホームとアウェイのデータを縦に結合
po_team_stats = pd.concat([po_home_stats, po_away_stats], ignore_index=True)
# チームごと・シーズンごとの平均を計算
po_season_team_stats = po_team_stats.groupby(['season_year', 'team_name']).agg({
'fg_pct': 'mean',
'fg3_pct': 'mean',
'ft_pct': 'mean',
'reb': 'mean',
'ast': 'mean',
'stl': 'mean',
'blk': 'mean',
'tov': 'mean',
'pts': 'mean',
'pts_against': 'mean',
'won': 'mean',
'fga': 'mean',
'fg3a': 'mean',
'fta': 'mean',
'pf': 'mean'
}).reset_index()
# 2PT 試投数の追加(FGA - FG3A)
po_season_team_stats['avg_2pa'] = po_season_team_stats['fga'] - po_season_team_stats['fg3a']
#Four Factorsの導入
po_season_team_stats['efg_pct'] = po_season_team_stats['fg_pct'] + 0.5 * (po_season_team_stats['fg3a'] / po_season_team_stats['fga']) * po_season_team_stats['fg3_pct']
po_season_team_stats['tov_pct'] = po_season_team_stats['tov'] / (po_season_team_stats['fga'] + 0.44 * po_season_team_stats['fta'] + po_season_team_stats['tov'])
po_season_team_stats['ftr'] = po_season_team_stats['fta'] / po_season_team_stats['fga']
# カラム名を分かりやすく変更
po_season_team_stats = po_season_team_stats.rename(columns={
'fg_pct': 'po_fg_pct',
'fg3_pct': 'po_fg3_pct',
'ft_pct': 'po_ft_pct',
'reb': 'po_reb',
'ast': 'po_ast',
'stl': 'po_stl',
'blk': 'po_blk',
'tov': 'po_tov',
'pts': 'po_pts',
'pts_against': 'po_pts_against',
'won': 'po_win_pct',
'fga': 'po_fga',
'fg3a': 'po_fg3a',
'fta': 'po_fta',
'pf': 'po_pf',
'avg_2pa': 'po_avg_2pa',
'efg_pct': 'po_efg_pct',
'tov_pct': 'po_tov_pct',
'ftr': 'po_ftr'
})
各々集計したデータを統合(マージ)し、優勝情報を付与します。
プレーオフは東西の上位8チームずつしか出場できないため、特徴量として正確にとらえられるように各年のチーム情報に出場の有無を追加します。
実行したコード
# 1. season_team_stats(レギュラー)と po_season_team_stats(プレイオフ)をマージ
merged_stats = season_team_stats.merge(
po_season_team_stats,
on=['season_year', 'team_name'],
how='left',
suffixes=('', '_po')
)
# 3. champion_label を merged_stats に付与
merged_stats['champion_label'] = merged_stats.apply(
lambda row: 1 if champions_dict.get(row['season_year']) == row['team_name'] else 0,
axis=1
)
# 4. プレイオフ出場有無をフラグで追加
merged_stats['made_playoffs'] = merged_stats['po_win_pct'].notna().astype(int)
# 5. champion_label の NaN は0に
merged_stats['champion_label'] = merged_stats['champion_label'].fillna(0).astype(int)
プレーオフの出場有無を追加できたら次に、プレーオフのシード情報を追加します。
実行したコード
# ファイルパスを指定
file_path = 'playoff_series_2010_2022.csv'
# Excelファイルを読み込む
playoff_series_df = pd.read_csv(file_path)
# 勝者と敗者のシード・ラウンド番号を統合
winners = playoff_series_df[['Yr', 'Winner_Team', 'winner_seed', 'round_num']].copy()
winners.columns = ['season_year', 'team_name', 'seed', 'round_num']
losers = playoff_series_df[['Yr', 'Loser_Team', 'loser_seed', 'round_num']].copy()
losers.columns = ['season_year', 'team_name', 'seed', 'round_num']
team_seed_df = pd.concat([winners, losers], ignore_index=True)
# merged_stats にマージ(season_year と team_name で結合)
merged_stats = merged_stats.merge(
team_seed_df,
on=['season_year', 'team_name'],
how='left'
)
# 欠損値を0で埋める
merged_stats['seed'] = merged_stats['seed'].fillna(0).astype(int)
merged_stats['round_num'] = merged_stats['round_num'].fillna(0).astype(int)
データの準備が完了したので、モデルを作成します。
モデル作成
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
# 目的変数
y = merged_stats['champion_label']
# 特徴量
X = merged_stats.drop(columns=['champion_label', 'season_year', 'team_name', 'po_win_pct', 'po_pts', 'po_pts_against', 'po_reb', 'po_ast', 'po_stl', 'po_blk', 'po_tov', 'made_playoffs'])
# 欠損値があれば0埋め
X = X.fillna(0)
# 訓練・テスト分割
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=42
)
# モデル作成と学習
model = RandomForestRegressor(random_state=42, n_estimators=500)
model.fit(X_train, y_train)
# 予測
y_pred = model.predict(X_test)
# 評価指標
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print(f"MSE: {mse:.4f}")
print(f"R2: {r2:.4f}")
MSE: 0.0307
R2: 0.5928
数値が低いため、XGboost(回帰)に変更し、再度実行します。
実行したコード
import xgboost as xgb
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
# 目的変数
y = merged_stats['champion_label']
# 特徴量
X = merged_stats.drop(columns=['champion_label', 'season_year', 'team_name', 'po_win_pct', 'po_pts', 'po_pts_against', 'po_reb', 'po_ast', 'po_stl', 'po_blk', 'po_tov', 'made_playoffs'])
# 欠損値があれば0埋め
X = X.fillna(0)
# データ分割
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=42)
# DMatrixの作成
dtrain = xgb.DMatrix(X_train, label=y_train)
dval = xgb.DMatrix(X_val, label=y_val)
# パラメータ設定
params = {
'objective': 'reg:squarederror',
'eval_metric': 'rmse',
'seed': 42,
'max_depth': 6,
'eta': 0.05,
'subsample': 0.8,
'colsample_bytree': 0.8,
'min_child_weight': 3,
'gamma': 0
}
# 学習
evals = [(dtrain, 'train'), (dval, 'eval')]
model = xgb.train(params, dtrain, num_boost_round=1000, early_stopping_rounds=50, evals=evals, verbose_eval=10)
# 予測
y_pred = model.predict(dval)
# 評価
mse = mean_squared_error(y_val, y_pred)
r2 = r2_score(y_val, y_pred)
print(f"MSE: {mse:.4f}")
print(f"R2: {r2:.4f}")
MSE: 0.0147
R2: 0.7634
特徴量の中での重要度を表示します。
実行したコード
import matplotlib.pyplot as plt
import xgboost as xgb
# 特徴量重要度プロット
xgb.plot_importance(model, max_num_features=20, importance_type='weight')
plt.show()
importance_dict = model.get_score(importance_type='weight')
importance_df = pd.DataFrame({
'feature': list(importance_dict.keys()),
'importance': list(importance_dict.values())
}).sort_values(by='importance', ascending=False)
print(importance_df.head(30))
分析結果が非常に向上し重要度の数値もすべて使えているので、これをモデルとして使用することに決定しました。
シュート確率はもちろん重要ですが、リバウンドがシュート関連以外の指標で一番高い数値を示しています。
これは納得のいく結果です。なぜリバウンドが重要な要素となるのか理由を解説します。
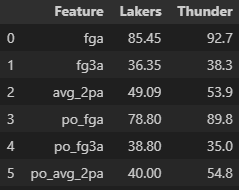
優勝チームの数値をもとにすると、サンダーのシュート成功率は約48%に対し、シュート試投数が92.7本/試合です。つまり約47本シュートが外れます。対戦相手も相当数のシュートが外れるので、1試合当たり90本近くのシュートが外れている計算となります。この外れた90本をいかに自チームのものにするかで、
セカンドチャンスの創出と、相手のオフェンスの終了そしてオフェンス機会の創出へとつながります。
そのため、リバウンドは重要といえます。
レイカーズの優勝を予測
レイカーズの去年の成績をモデルに充てるために、レイカーズのデータをインポートし、作成したモデルを使用します。
実行したコード
lakers_2024_df = pd.read_excel("Lakers_2024-2025.xlsx")
lakers_2024_df.columns
lakers_2024_df = lakers_2024_df.rename(columns={'round': 'round_num'})
# 特徴量リスト
features = ['fg_pct', 'fg3_pct', 'ft_pct', 'reb', 'ast', 'stl', 'blk', 'tov', 'pts', 'pts_against',
'won', 'fga', 'fg3a', 'fta', 'pf', 'avg_2pa', 'efg_pct', 'tov_pct', 'ftr',
'po_fg_pct', 'po_fg3_pct', 'po_ft_pct', 'po_fga', 'po_fg3a', 'po_fta',
'po_pf', 'po_avg_2pa', 'po_efg_pct', 'po_tov_pct', 'po_ftr',
'seed']
# 特徴量を抽出
X_lakers = lakers_2024_df[features]
# XGBoost用のDMatrixに変換
d_lakers = xgb.DMatrix(X_lakers)
# 予測
lakers_pred = model.predict(d_lakers)
# 優勝確率の出力
print(f"レイカーズの優勝確率(予測スコア): {lakers_pred[0]:.4f}")
レイカーズの優勝確率(予測スコア): 0.0036
レイカーズの優勝の可能性は0.4%と非常に厳しい予測が出ました。
それではどんな数値が予測に影響したかを見ていきます。
スタッツ内の確率を比較します。
実行したコード
import matplotlib.pyplot as plt
import numpy as np
# 特徴量のラベル
features = comparison_rate['Feature']
x = np.arange(len(features))
# 値の取得
champion_means = comparison_rate['Champion_Mean']
lakers_values = comparison_rate['Lakers']
plt.figure(figsize=(12, 6))
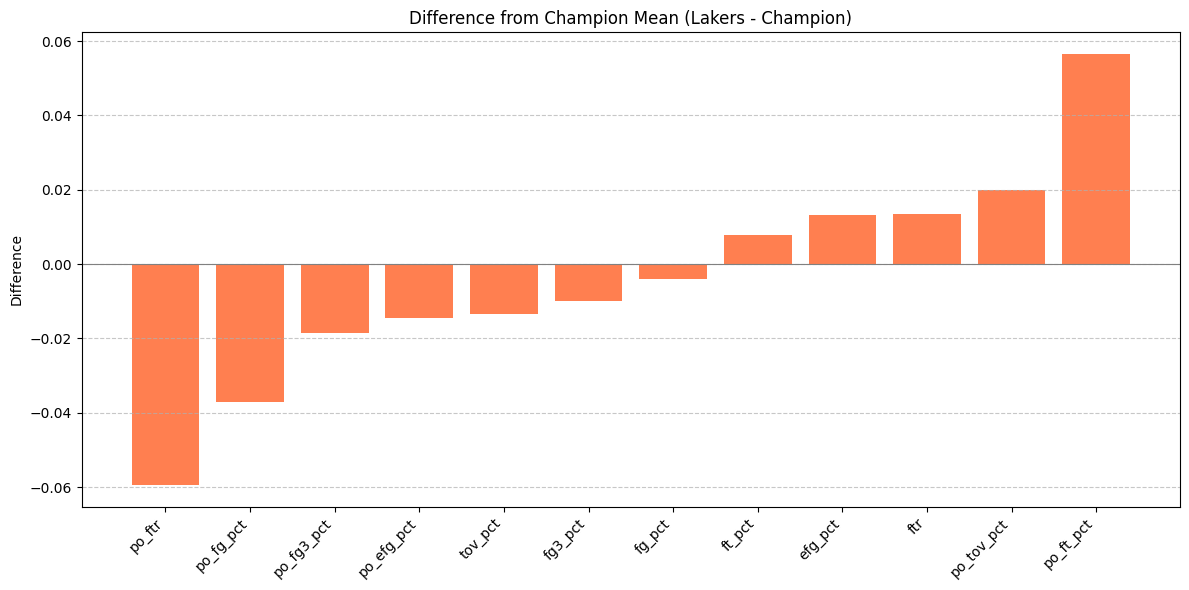
plt.bar(features, comparison_rate['Difference'], color='coral')
plt.axhline(0, color='gray', linewidth=0.8)
plt.xticks(rotation=45, ha='right')
plt.title('Difference from Champion Mean (Lakers - Champion)')
plt.ylabel('Difference')
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.tight_layout()
plt.show()
確率面においてシュート精度が優勝チームの数値からみて低いことがうかがえます。
全体の特徴量もどのような数値か確認していきます。
実行したコード
rate_features = ['fg_pct', 'fg3_pct', 'ft_pct', 'reb', 'ast', 'stl', 'blk', 'pts', 'pts_against', 'won', 'fga', 'fg3a', 'fta', 'pf', 'avg_2pa', 'efg_pct', 'tov_pct', 'ftr', 'po_fg_pct', 'po_fg3_pct', 'po_ft_pct', 'po_fga', 'po_fg3a', 'po_fta', 'po_pf', 'po_avg_2pa', 'po_efg_pct', 'po_tov_pct', 'po_ftr']
comparison_rate = comparison_df[comparison_df['Feature'].isin(rate_features)].copy()
comparison_rate = comparison_rate.sort_values(by='Difference')
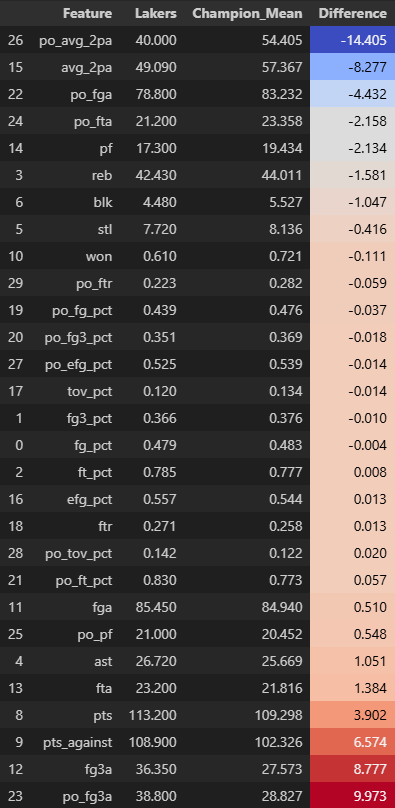
comparison_rate[['Feature', 'Lakers', 'Champion_Mean', 'Difference']].style \
.background_gradient(cmap='coolwarm', subset=['Difference']) \
.format(precision=3)
全体的な指標があまりよくないことがうかがえます。
全体のシュート成功率はほとんど平均通りですが,、2ptで落とした確率を、3pt成功率でカバーしておりかなり不安定です。なぜなら、3pt確率は遠い距離からなので安定しにくいからです。
シュート試投回数も平均から低いことも気になるポイントです。
ディフェンスに関する指標も全体的に低く、オフェンス権を奪うことができていないと想像できます。
昨年のチャンピオンも解析
昨年度の優勝チームOklahoma City Thunder(以降サンダー)も予測し、具体的に何が足りなかったかを検証していきます。
実行したコード
# 特徴量リスト
features = ['fg_pct', 'fg3_pct', 'ft_pct', 'reb', 'ast', 'stl', 'blk', 'tov', 'pts', 'pts_against',
'won', 'fga', 'fg3a', 'fta', 'pf', 'avg_2pa', 'efg_pct', 'tov_pct', 'ftr',
'po_fg_pct', 'po_fg3_pct', 'po_ft_pct', 'po_fga', 'po_fg3a', 'po_fta',
'po_pf', 'po_avg_2pa', 'po_efg_pct', 'po_tov_pct', 'po_ftr',
'seed']
# 特徴量を抽出
X_thunder = thunder_2024_df[features]
# XGBoost用のDMatrixに変換
d_thunder = xgb.DMatrix(X_thunder)
# 予測(すでに訓練済みの model を使用)
thunder_pred = model.predict(d_thunder)
# 結果出力(優勝確率の予測値)
print(f"サンダーの優勝確率(予測スコア): {thunder_pred[0]:.4f}")
サンダーの優勝確率(予測スコア): 0.2157
サンダーの優勝確率は21.6%と出ました。
結果に大きく差が出る結果となりました。サンダーとレイカーズにはどのようなチーム力の差があるのか見てみます。
学習時にも大きく占有率を占めていたシュート確率をグラフ化して確認していきます。
シュート試投数の平均値と確率を同時に出力すると、数値が乖離するため二つのグラフを出力します。
シュート面での確率差をグラフで出力します。
チャンピオンとの差を見てみる
実行したコード
import pandas as pd
import matplotlib.pyplot as plt
# 特徴量リスト
rate_features = ['fg_pct', 'fg3_pct', 'ft_pct', 'po_fg_pct', 'po_fg3_pct', 'po_ft_pct',
'efg_pct', 'po_efg_pct', 'tov_pct', 'po_tov_pct', 'ftr', 'po_ftr']
# 1行目の特徴量だけ取り出す(Series型)
lakers_data = lakers_2024_df[rate_features].iloc[0]
thunder_data = thunder_2024_df[rate_features].iloc[0]
# DataFrame化
comparison_df_plot = pd.DataFrame({
'Feature': rate_features,
'Lakers': lakers_data.values,
'Thunder': thunder_data.values
})
# グラフ表示
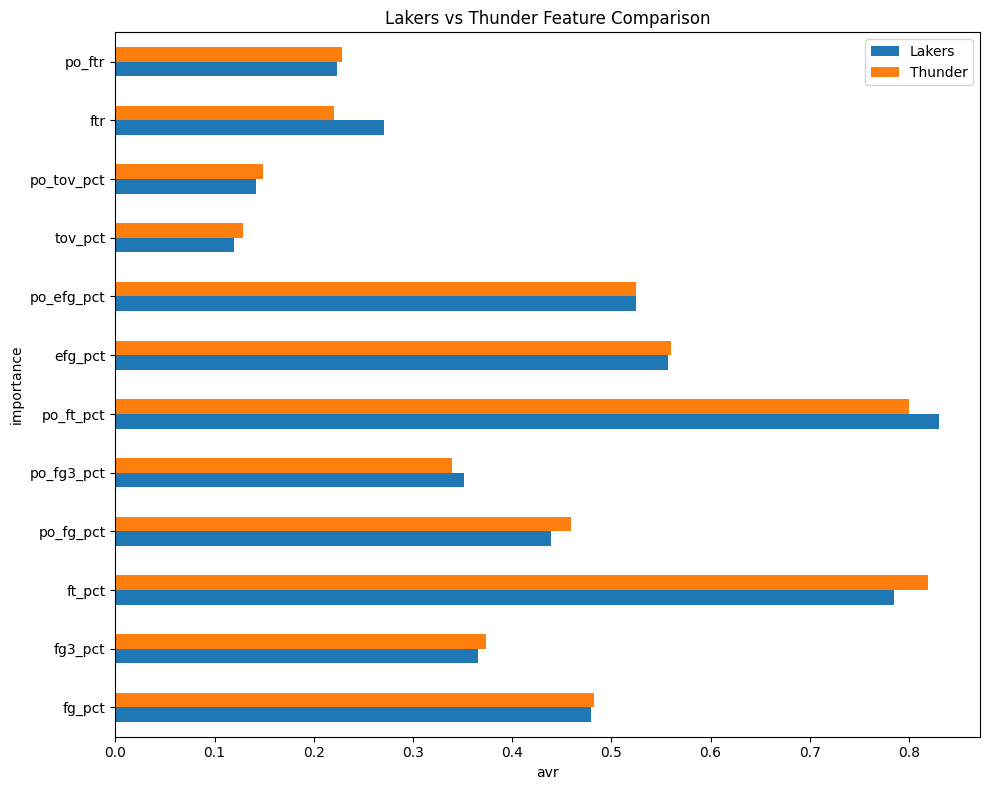
comparison_df_plot.set_index('Feature').plot(kind='barh', figsize=(10, 8))
plt.title("Lakers vs Thunder Feature Comparison")
plt.xlabel("avr")
plt.ylabel("importance")
plt.tight_layout()
plt.show()
グラフ上ではわずかですが成功率の差なのでかなりの差といえます。
シュートの試投数を見てみます。
実行したコード
import pandas as pd
import matplotlib.pyplot as plt
# 特徴量リスト
rate_features = ['fga', 'fg3a', 'avg_2pa', 'po_fga', 'po_fg3a', 'po_avg_2pa']
# 1行目の特徴量だけ取り出す(Series型)
lakers_data = lakers_2024_df[rate_features].iloc[0]
thunder_data = thunder_2024_df[rate_features].iloc[0]
# DataFrame化
comparison_df_plot = pd.DataFrame({
'Feature': rate_features,
'Lakers': lakers_data.values,
'Thunder': thunder_data.values
})
# グラフ表示
comparison_df_plot.set_index('Feature').plot(kind='barh', figsize=(10, 8))
plt.title("Lakers vs Thunder Feature Comparison")
plt.xlabel("avr")
plt.ylabel("importance")
plt.tight_layout()
plt.show()
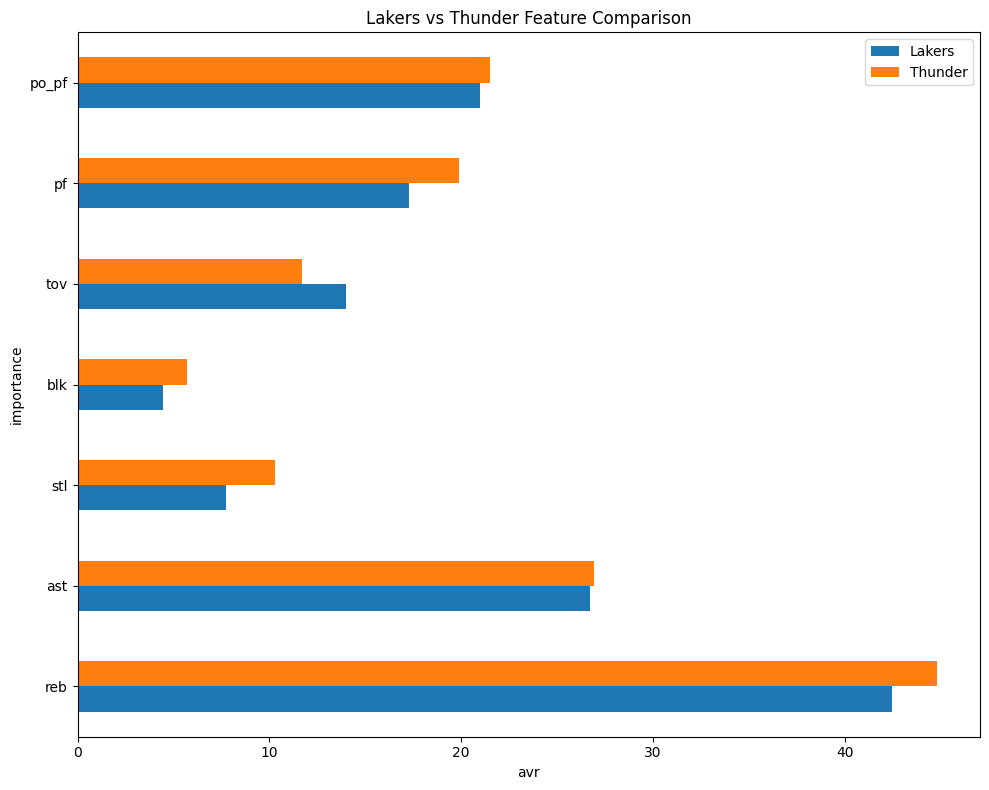
シュート本数の平均値に関しても大きく差が見られます。これはシュートせずに攻撃が終了している可能性が非常に高いか、もしくは、オフェンス回数の絶対量が少ない可能性が考えられます。
その数値を検証するためリバウンドやミス(tov)、ディフェンス面の数値も確認していきます。
実行したコード
import pandas as pd
import matplotlib.pyplot as plt
# 特徴量リスト
rate_features = ['reb', 'ast', 'stl', 'blk', 'tov', 'pf', 'po_pf']
# 1行目の特徴量だけ取り出す
lakers_data = lakers_2024_df[rate_features].iloc[0]
thunder_data = thunder_2024_df[rate_features].iloc[0]
# DataFrame化
comparison_df_plot = pd.DataFrame({
'Feature': rate_features,
'Lakers': lakers_data.values,
'Thunder': thunder_data.values
})
# グラフ表示
comparison_df_plot.set_index('Feature').plot(kind='barh', figsize=(10, 8))
plt.title("Lakers vs Thunder Feature Comparison")
plt.xlabel("avr")
plt.ylabel("importance")
plt.tight_layout()
plt.show()
ディフェンス面に明らかな差が見られます。特にスティール、リバウンドに差があります。
又、tov率が高くレイカーズはサンダーに比べるとオフェンス権を手放しがちという傾向も可視化されました。
その中でもリバウンド回数が特に差が多く、サンダーが攻守ともに高いアドバンテージを持っていることがわかります。
アシストに関してはほとんど差がなくチャンスメイクに関しては同等にできているといえます。
オフェンスの絶対数=リバウンド数とシュート確率、細かなミスによるオフェンスの終了に原因があることがわかりました。
分析した情報から得られた情報
リーグ全体の傾向
シュート成功率がもっとも重要である。
シュート成功率の中でも、3ポイント成功率が特に重要視されている傾向。
プレーオフ時にも同様のことがいえる。
シュート面以外では、リバウンドが最も重要。
レイカーズの課題と改善目標
①リバウンド数(reb)の向上
42.43/gはリーグ中26位です。昨年のリーグ平均が44本なので、45/gを目標にしましょう。
②シュート試投数(fga)の向上
85.45/gはリーグ最下位です。リーグ平均は89.2/gなので、92/gを目標にしましょう。
③上記二点を達成するための守備戦術の見直しが必要です。
stl数7.72/gは全体平均から少し低い指標です。blkも全体平均を少し割っていて、ディフェンスのプレッシャーが弱く感じられます。新しいトラップフェンスや、ディフェンスの連携力向上にチームで取り組むべきだと思います。
考察
リバウンドの数値から考えられることとしては、やはり昨シーズン中のトレード(選手の移籍)が頭に浮かびます。
ルカ・ドンチッチ獲得時にトレードされたアンソニー・デイビスは優秀なセンター(※センターとは、ゴールに最も近いインサイドポジション)でした。ドンチッチも非常に優秀なアウトサイドプレイヤーで攻撃面を補強できたと思いますが、リバウンド面において代償を背負った結果となったのではないでしょうか。
課題となるリバウンド数はシュート本数向上の解決に直結しているため、マストで修正が必要と思います。
3ptの確率はかなり良好ですが、インサイドが弱みになると外へのプレッシャーが強くなります。3ptは今の時代には不可欠なので、長所を失う前に早めの立て直しが必要だと思います。
戦術面以外の提案としてリバウンド特化のインサイドプレイヤーと、守備力に長けたアウトサイドプレイヤーの獲得を検討してもいいかもしれません。
レイカーズの優勝確率は0.3%と非常に厳しい確率ですが、プレーオフ参加ラインには達しているので、優勝の芽が全くないとは思いません。しかし、明確な課題はあるのでぜひ修正して来シーズンを迎えてほしいです。
がんばれ、レイカーズ!
まとめ
今回の予想にチャレンジしてみて、データの重要性を改めて実感しました。
NBAを普段見ることはあまりないですが、数値を解析することでここまでチームの改善点や、状況を把握できることに驚きました。
具体的な反省点としては、リバウンドの内訳があるデータにたどり着けなかったことで、
精度を少し下げてしまったと感じています。フォーファクターといわれる、重要項目の成績を重みづけして計算された4つの指標といわれています。通常の成績よりも正確に出せたのではないかと思います。
もう一つがグラフ化した時に、数値が低い方が良い指標もありながら、すべてを一緒にしてしまったこと。
もしまた同じ分析をするならフォーファクターの導入と、新たな取り組みとして取り上げたチームの個人成績も盛り込んでもっと詳細な内容までフォーカスできたらと思います。!