動機
Xでとある人のポストから「Exponential Idle」というアプリに辿り着いたのだが、そのアプリ内でミニゲームとして用意されていた物の内矢印パズルというものが面白そうだったので軽く解法を研究してみた。
パズルのルール
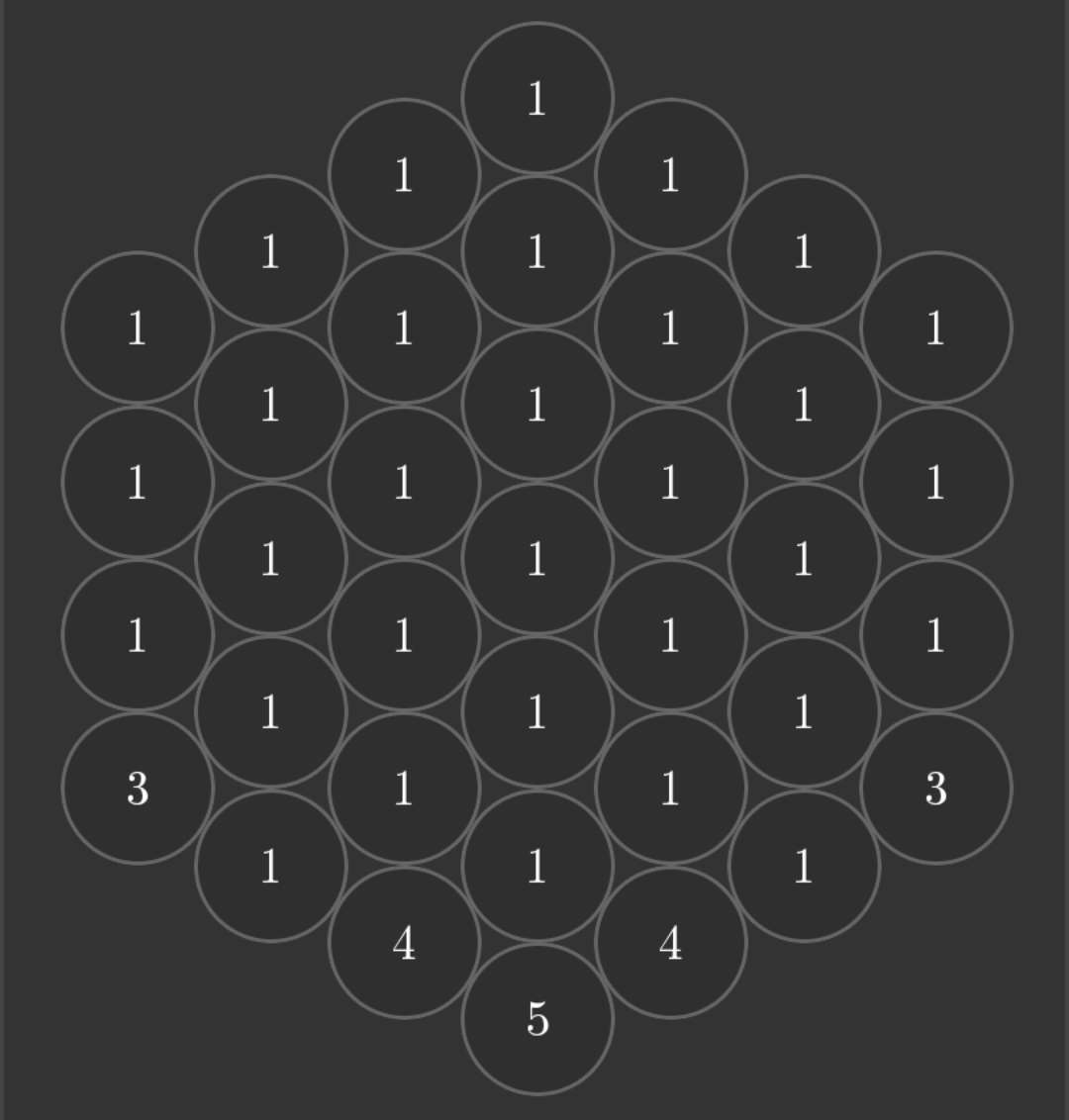
まず、パズルを開始すると下図のような盤面が生成される(元々の表示は矢印だがわかりやすいため設定から数字で表示するようにしている)。
それぞれの数字の書かれたマスをタップするとそのマスとその周囲に隣接したマスの数字に1が足される。ただし、マスに書かれた数字が6であれば1になる。ゴールは、全てのマスを1にするという至ってシンプルな構造である。
具体的な解法
まずは器械的に解く解法を示す。説明の簡単のため、縦方向と斜め方向に文字を振っておいた。7Dは1、1Aは2、2Eは5という具合になっている。
まずは盤面を生成したら、上から順に下にマスが存在する全てのマス(1A,1B,1C,1D,2E,3F,4G以外全てのマス)について、自身の数値が1になるまで真下のマスをタップし続けるという操作を行う。この操作は今後も使うので、ここではこの操作を「数字を下ろす」などと表現する。この操作をすることで盤面がみるみるうちに1で染まっていく。
次に、1Dを3で割ったあまりについて、
・0なら7Gを1回押す
・1なら何もしない
・2なら7Gを2回押す
そしたら、4Gから1Dを引いた数値を3で割ったあまりについて、
・0なら何もしない
・1なら7Fを2回押す
・2なら7Fを1回押す
それができたら、数字を下ろす。
すると、盤面が1と4のみで構成されるようになる。
ここで、
・3Fが4なら7Eを3回押す。
・2Eと3Fの差が3なら7Fを3回押す。
・4Gが4なら7Gを3回押す。
それで数字を下ろせば、全面が1になってクリアとなる。
この解法の理由
このパズルは最初にも述べたようにライツアウトの拡張版だと考えることができる。つまりライツアウトの解法が通用すると考えることができる。先程定義した数字を下ろすという概念はライツアウトから持ってきたもので、実際にかなりライツアウトでの考え方が活きてくる。
ライツアウトを解くにあたって大事な方針は、「いかに簡単な連立方程式を生成するか」である。数字を下ろすという概念も、できるだけ多くのマスに対し、固定した役割を与えることでその分の自由度を減らし連立方程式の変数を減らすことに通じている。通常、なんの工夫もしなければマスの数だけの変数が含まれた連立方程式を解く羽目になるが、今回の場合であれば1番上段の7マス(4A,5B,6C,7D,7E,7F,7Gのこと。今後最上段と呼ぶ。)以外は「1つ上のマスを1にするまで押す」という役割を持っているので、変数を7個まで減らすことができる。
変数を減らしたら、実際に連立方程式を作るための情報を集める。全部1の盤面で最上段の7マスそれぞれについて、1回だけ押してから数字を下ろすという操作をすると、1番下段の7マス(1A,1B,1C,1D,2E,3F,4Gのこと。今後最下段と呼ぶ。)の数字が変わる。これがどれだけ増加するかを調べる。
押したマスとそこで数字を下ろした後の最下段の数字を左から順に並べたものを列挙すると、
| 押すマス | 数字 |
|---|---|
| 7G | 1401041 |
| 7F | 4230324 |
| 7E | 0333330 |
| 7D | 1035301 |
この時点で対称性があることに気付く。7Gを押すことと4Aを押すことは同義であり、同様に7Fと5B、7Eと6Cも同義である。つまりこれ以上の調査はいらないことになる。
ここでmod6のまま考えると連立方程式が面倒なことになってしまうので、mod3とmod2に分けて考えることにする。また、対称性より最下段の左側3マスは無視できるので、右4マスの数字の増加分だけ書く。その下で再び列挙すれば、
| 押すマス | mod6 | mod3 | mod2 |
|---|---|---|---|
| 7G | 1041 | 1011 | 1001 |
| 7F | 0324 | 0021 | 0100 |
| 7E | 3330 | 0000 | 1110 |
| 7D | 5301 | 2001 | 1101 |
まず全マスをmod3で1にする。そのためにどのマスを押すかを考える。7Eに注目すると0000なので押したところで変化がない。また、7Gを2倍して7Fを引けば7Dとなるのでこれらの内2つのマスのみを押せばよいことがわかる。よって7Dを除外して7Gと7Fだけ考慮すればよい。そして変数が2つなので、盤面が解けるように生成されているならば連立する式も2つで十分である。因みに、もし盤面がランダムで解けるかどうかも不明だった場合はちゃんと全て連立させて解の存在を考える必要がある。
連立する式として、2Eの数字についての式はどのマスにも影響を及ぼさないので適さない。ここで1D,3F,4Gの内2つの式を選ぶ必要があるが、ここでは0と1のみでできていて計算が簡単そうな1Dと4Gを選ぶ。1Dに関与できるのは7Gのみなのでまず1Dを3の倍数にするように7Gを押す。そうしてできた条件が、
「1Dを3で割ったあまりについて、
・0なら7Gを1回押す
・1なら何もしない
・2なら7Gを2回押す」
というものである。次に4Gについて、7Gを押した回数を考慮して7Fの押す回数を考える必要がある。7Gの押す回数は1Dの数値に依存しているから、それを利用して4Gと1Dの差を取ると、うまい条件を作ることができる。
「4Gから1Dを引いた数値を3で割ったあまりについて、
・0なら何もしない
・1なら7Fを2回押す
・2なら7Fを1回押す」
この操作の上で数字を下ろすと、3で割って1余る数値以外を消せるので1と4のみになる。これらを白と黒に見立てればかなりライツアウトに近い見た目となることがわかるだろう。次に、mod2の方について考える。これもmod3と同様の考え方で行けば、7G+7F=7Dより7Dを消して計算しやすそうな3つの式を取り出す。2E,3F,4Gを見れば、7Gのみが4Gに干渉できる。また、7Eのみが3Fに干渉でき、最後に7Fの7Eとの兼ね合いを考えて2Eに注目すれば、
・3Fが4なら7Eを3回押す。
・2Eと3Fの差が3なら7Fを3回押す。
・4Gが4なら7Gを3回押す。
という条件ができあがる。ここで3回押してるのは1と4以外の数字を増やさず、mod2で考えたことを活用するためである。また、さっきの表は1回分だったのに3回押しても良いのか疑問になる人もいるかもしれないが、3回押してmod2を取れば1回押したことと同じなので表の数字から変更する必要はない。
この操作をした上で数字を下ろせば、盤面が全て1となりクリアとなる。
最後に
今回の場合mod6の問題だったのでmod3とmod2に分解して考えることができたが、一般にmodnで作られた問題はnの素因数に分解して考えられるので、基本modp(pは素数)について解けばよい。また、一般的には正方形のライツアウトだが、今回のような六角形や他の形にも「連立方程式の変数を減らす」という方針の下で考えれば解き方を生み出すことができる。simon tatham's portable puzzle collectionというサイト(アプリもあるよ!)で白黒しかないが自分で指定して様々なライツアウトが解けるのでそこで連立方程式を自分で減らしてみて是非楽しんでいただきたい。