例えば、いくつもの測定結果があって一定の範囲内に分布するものだけを製品としたい場合に、一つづつ確認してもいいけど、ざっと計算して基準内にあるかどうか統計的に求め方法があるよというのがマハラノビス距離。
また、同種類だったり同じものだけど測定結果が諸条件で変わるときに、同じものか違う種類かを統計的に判断する方法としても使える。極論言えば、慣れた人間の判断力にはかなわないわけだが、統計的にという安心材料を追加できることは間違いない。
ここではアヤメのデータを使って説明していこうと思う。ざっと概要を説明するとアヤメの花びらとがくそれぞれの長さと幅を50個ずつ3種類測定したデータでsetosaとversicolor、virginicaという3種類ある。これ以上詳しい話はググればだれか書いてると思う。
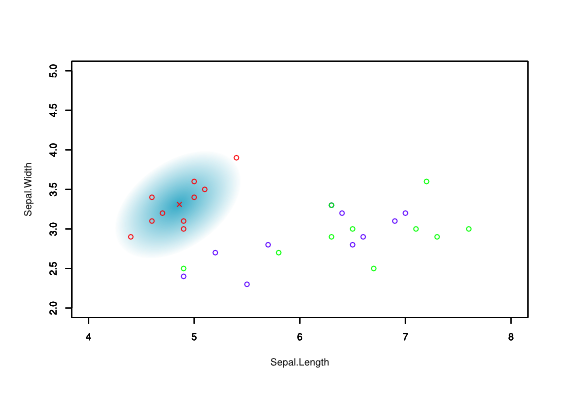
絵的に説明するためとりあえず2変量で話を進める、花弁の長さと幅をそれぞれx軸とy軸として、プロットしとみると、下の図のようになる。
今回は例としてアヤメデータから種類毎に10個ずつ取り出して○点でプロットしてみた、setosaか否かを判別することにしたので、setosa群の平均点を×点で示している。また、確率分布のイメージを青のグラデーションで示してみた。マハラノビス距離はこの中心(×点)から各○点までの距離を計算する。
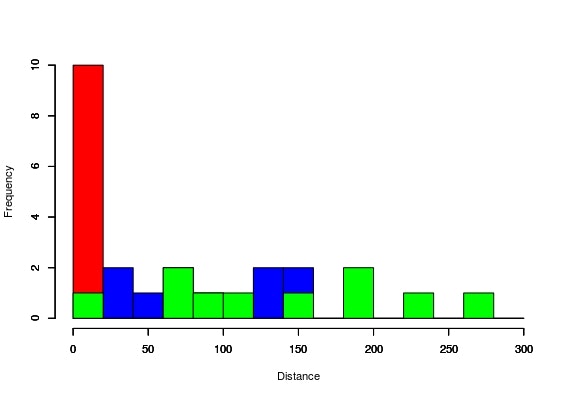
で、計算した結果を横軸を距離、縦軸を度数としてヒストグラムにプロットすると次のようになる。
Rのプロットが大変なんでこの手のプロットをすると一部データが表示されていない時もあるけど、小さな値の部分に赤で示したsetosaが分布しており、距離が増えるにしたがってそれ以外のものが分布している。2変量だとこんな感じ、結果としてはいまいちだね~。
マハラノビス距離では、この分布の中心からに距離を、分散状況を踏まえ計算する。そのため、マハラノビス汎距離とも呼ばれているが、そんなことはどうでもいい。ユークリッド距離との違いはこの分散を考慮して計算する点で異なる。で、ここからは4変量で計算する。
> ## create test and training set
> train_index <- c(1:10)
> train <- iris[train_index,]
> test <- iris[-train_index,]
>
> ## Training (setosa)
> center <- apply(train[,1:4], 2, mean)
> covar <- cov(train[,1:4])
>
> ## Calculate distance
> mahalanobis( test[1,1:4], center, covar ) #setosa
11
4.85708
> mahalanobis( test[41,1:4], center, covar ) #versicolor
51
1424.809
> mahalanobis( test[91,1:4], center, covar ) #virginica
101
3176.181
上の例では,setosaの最初の10個が基準データとしてそれぞれの種類でどのように距離が変わるのかを示している。
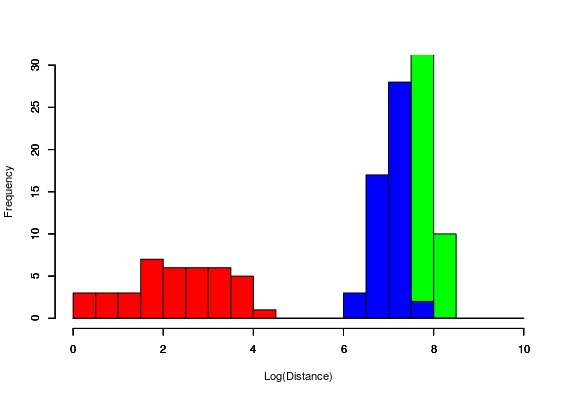
ちなみこれをヒストグラムで表すと以下のようになる。
基準としたものと同じ種類のもの方が、0の付近に分布していることがわかる。つまり、似たよう測定結果のものは同じところに集まるわけで、一定以下の値を取るようにすれば、大量のデータを比較する必要がなくなるわけだ。
4変量にするとだいぶはっきり分かれてくれたけど、最近流行りのビッグデータで注意しないといけないのは、いわゆる「次元ののろい」というやつ何でも多けりゃいいってもんじゃないよって話。
ま、こんな感じ