2024/02/12追記
ChatGPTにコードを修正してもらいました:
# 回路方程式を入力
cir_eq = """
ZP = RP / (1 + s*CP*RP)
ZM = RM / (1 + s*CM*RM)
VIN = (s*LP + ZP + ZM)*IT
VOUT = ZM * IT
"""
# 未知数と求めたい変数を入力
unknown_parameters = "ZP, ZM, IT, VOUT"
wanted_parameter = "VOUT"
# ----------------
# 以下、ユーザーが修正する箇所なし
from sympy import Symbol, solve, Eq, latex, collect, expand, numer, denom, sympify
from IPython.display import Math
import re
# シンボル生成
symbol_names = set(re.findall(r'\b[A-Za-z]+\b', cir_eq))
symbols_dict = {name: Symbol(name, real=True) for name in symbol_names}
unknown_parameters_list = [symbols_dict[param.strip()] for param in unknown_parameters.split(',')]
# TeX表示用の配列を生成
cir_eq_tex = [name[0] + "_{" + name[1:] + "}" if len(name) > 1 else name for name in symbol_names]
# 方程式をSymPyの式として解析
cir_eq_list = cir_eq.strip().split('\n')
equations = []
for eq in cir_eq_list:
lhs, rhs = eq.split('=')
equation = Eq(sympify(lhs, locals=symbols_dict), sympify(rhs, locals=symbols_dict))
equations.append(equation)
# 方程式を解く
solutions = solve(equations, unknown_parameters_list, dict=True)
if solutions:
solution = solutions[0]
wanted_solution = solution[symbols_dict[wanted_parameter]]
solution_simplified = collect(expand(numer(wanted_solution)), Symbol("s")) / \
collect(expand(denom(wanted_solution)), Symbol("s"))
# 式をTeX形式で表示
sol_tex = wanted_parameter + " = " + latex(solution_simplified)
replacement_mapping = dict(zip(symbol_names, cir_eq_tex))
for old, new in replacement_mapping.items():
sol_tex = sol_tex.replace(old, new)
display(Math(sol_tex))
else:
print("解を見つけることができませんでした。")
はじめに
アナログ回路設計者です。最近、趣味でPythonの勉強を始めました。
アナログ回路の設計業務において、SPICEによる数値解析回路シミュレータがよく使われます。しかし数値解析シミュレータだけでは、設計している回路の理解が深まりません。時には設計している回路を単純化し、回路方程式を立て、これを解くということも必要です。
回路方程式を解くのは手間がかかる作業です。とりあえず解いてみたはいいが、計算ミスがあって有益な結果が得られなかった、得られた式が複雑で洞察が得られず解く必要がなかった、など、時間の割には成果が得られにくいとも言えます。
そこで今回、Sympyを使って回路方程式を解けるようにしました。プログラムを作成するにあたっては、人間が入力する箇所を出来るだけ減らすということを意識しました。
※Pythonは勉強を始めたばかりですので、本記事におけるコードは不適切だったり冗長な箇所があるかもしれません。
こんな人向け
・回路設計を解くことに疲れた回路設計者
・pythonとJupyter-notebookを使って遊んだことがある
・sympyも少しだけ触ったことがある
想定している状況は以下の通りです
「ノートに回路図を描いて方程式を立てるまでは終わらせた。方程式の数が多くて、これを解くのは時間がかかりそうだ。 解いても意味のある結果が得られるか分からないし・・・。よし、sympyにやらせよう!」
環境
Python: 3.7.4、SymPy: 1.6.2
解析する回路
簡単な例として下図の回路の伝達関数を計算してみましょう。回路の部品定数は数値ではなく記号としています。
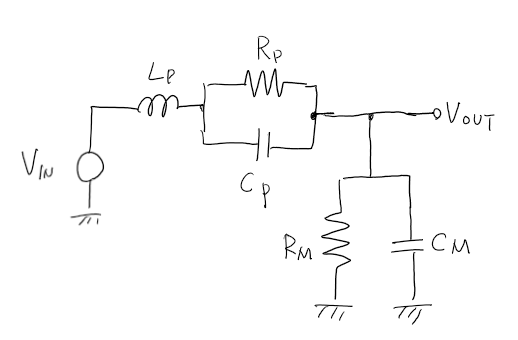
まずは下図のように自力で回路方程式を立てましょう。sympyに回路方程式を解かせるとなると、方程式の数を減らす工夫をしなくて良いため、頭のエネルギーが節約できます。

未知数(ここではZP, ZM, IT, VOUT)と方程式の数が一致していることを確認したら回路方程式の作成は終わりです。
ではここから先はJupyter-notebook上で実行していきましょう。
全コード
いきなりですが、全コードは以下の通りです。
# 回路方程式を入力
ce = """
ZP = RP / (1 + s*CP*RP)
ZM = RM / (1 + s*CM*RM)
VIN = (s*LP + ZP + ZM)*IT
VOUT = ZM * IT
"""
# 未知数を入力
uk = "ZP, ZM, IT, VOUT"
#求めたい変数を入力
wn = "VOUT"
#----------------------------------------------------
# 以下、ユーザーが入力する箇所は無し
# 初期設定
from sympy import *
from IPython.display import Math
from collections import Counter
# 回路方程式から記号を抽出し、Symbolとして宣言
rep_char = ["+", "-", "*", "/", "s", "=", "\n", "(", ")"]
ce_rep = ce
for i in range(len(rep_char)):
ce_rep = ce_rep.replace(rep_char[i], " ")
ce_sym = ce_rep.split()
ce_sym = list(Counter(ce_sym).keys())
for i in reversed(range(len(ce_sym))): # リスト中の数字を消去
if ce_sym[i].isdecimal():
del ce_sym[i]
s = Symbol("s", real=True)
for i in range(len(ce_sym)):
exec(ce_sym[i] + " = Symbol(\"" + ce_sym[i] + "\", real=True)")
# TeX表示用の配列を生成
ce_tex = []
for i in range(len(ce_sym)):
if len(ce_sym[i]) == 1:
ce_tex.append(ce_sym[i][0])
else:
ce_tex.append(ce_sym[i][0] + "_{" + ce_sym[i][1:] + "}")
# 回路方程式と未知数のシンボルリストを生成
start = 3
ind_eq = -1
ind_rt = 2
ce_sol = []
while True:
ind_eq = ce.find("=", ind_eq+1)
ind_rt = ce.find("\n", ind_rt+1)
if ind_rt == -1:
break
exec("ce_sol.append(" + ce[start:ind_eq] + "-(" + ce[ind_eq+1: ind_rt] + "))")
start=ind_rt + 1
exec("uk_sol = " + uk)
exec("wn_sol = " + wn)
# 方程式を解いて整理する
if len(uk_sol) != len(ce_sol):
print("未知数と方程式の数を揃えて下さい。")
else:
sol = solve(ce_sol, uk_sol, dict=True)[0][wn_sol]
# 分母分子を整理する
nu = collect(expand(numer(sol)), s) # Numerator、分子
de = collect(expand(denom(sol)), s) # denominator、分母
sol = nu / de
#式の表示
sol_tex = latex(sol)
for i in range(len(ce_sym)):
sol_tex = sol_tex.replace(ce_sym[i], ce_tex[i])
display(Math(sol_tex))
これを実行すると以下の結果が得られます。
$$\displaystyle \frac{C_{P} R_{M} R_{P} V_{IN} s + R_{M} V_{IN}}{C_{M} C_{P} L_{P} R_{M} R_{P} s^{3} + R_{M} + R_{P} + s^{2} \left(C_{M} L_{P} R_{M} + C_{P} L_{P} R_{P}\right) + s \left(C_{M} R_{M} R_{P} + C_{P} R_{M} R_{P} + L_{P}\right)}$$
ではプログラムの流れとその詳細について解説していきましょう。
STEP1: 回路方程式と未知数を入力する
# 回路方程式を入力
ce = """
ZP = RP / (1 + s*CP*RP)
ZM = RM / (1 + s*CM*RM)
VIN = (s*LP + ZP + ZM)*IT
VOUT = ZM * IT
"""
# 未知数を入力
uk = "ZP, ZM, IT, VOUT"
#求めたい変数を入力
wn = "VOUT"
回路方程式、未知数、そして求めたい変数を入力します。回路方程式を入力するにあたっては、s以外のパラメータは大文字から始めるようにします。これは計算結果をTeX表示する際の処理において小文字だと不都合があるためです。
STEP2: モジュールをインポート
from sympy import *
from IPython.display import Math
from collections import Counter
モジュールをインポートします。特に解説は必要ないでしょう。
STEP3: 回路方程式から記号を抽出し、Symbolとして宣言
rep_char = ["+", "-", "*", "/", "s", "=", "\n", "(", ")"]
ce_rep = ce
for i in range(len(rep_char)):
ce_rep = ce_rep.replace(rep_char[i], " ")
ce_sym = ce_rep.split()
ce_sym = list(Counter(ce_sym).keys())
for i in reversed(range(len(ce_sym))): # リスト中の数字を消去
if ce_sym[i].isdecimal():
del ce_sym[i]
ここでは以下のような処理をしています
(i) STEP1にて回路方程式ceが入力される
ZP = RP / (1 + sCPRP)
ZM = RM / (1 + sCM+RM)
VIN = (sLP + ZP + ZM)*IT
VOUT = ZM * IT
(ii) 入力した回路方程式(STEP1のce)から演算子(+-*/), s, 改行(\n)などをスペースに置換する
ce_rep:
ZP RP 1 CP RP ZM RM 1 CM RM VIN LP ZP ZM IT VOUT ZM IT
(iii) 方程式中に登場する記号を抽出する
ce_sym:
['ZP', 'RP', '1', 'CP', 'ZM', 'RM', 'CM', 'VIN', 'LP', 'IT', 'VOUT']
(iii) 上で求めたリストから数字を見つけて消去する(この場合1が消去される)
ce_sym:
['ZP', 'RP', 'CP', 'ZM', 'RM', 'CM', 'VIN', 'LP', 'IT', 'VOUT']
上の処理で回路方程式中に使用されている記号のリストが得られたので、
SympyのSymbolとして宣言します。
s = Symbol("s", real=True)
for i in range(len(ce_sym)):
exec(ce_sym[i] + " = Symbol(\"" + ce_sym[i] + "\", real=True)")
execで実行されてるコード:
ZP = Symbol("ZP", real=True)
RP = Symbol("RP", real=True)
CP = Symbol("CP", real=True)
ZM = Symbol("ZM", real=True)
RM = Symbol("RM", real=True)
CM = Symbol("CM", real=True)
VIN = Symbol("VIN", real=True)
LP = Symbol("LP", real=True)
IT = Symbol("IT", real=True)
VOUT = Symbol("VOUT", real=True)
STEP4: TeX表示用の配列を生成
ce_tex = []
for i in range(len(ce_sym)):
if len(ce_sym[i]) == 1:
ce_tex.append(ce_sym[i][0])
else:
ce_tex.append(ce_sym[i][0] + "_{" + ce_sym[i][1:] + "}")
出力結果をTeXで表示したいため、これ用のリストを作成します。
ce_symのリストをもとに、2文字目以降は下付きにするリストce_texを生成しています1。
例: VOUT → V_{OUT}、$V_{OUT}$
ce_tex:
['Z_{P}', 'R_{P}', 'C_{P}', 'Z_{M}', 'R_{M}', 'C_{M}', 'V_{IN}', 'L_{P}', 'I_{T}', 'V_{OUT}']
(参考)STEP3で求めたce_sym:
['ZP', 'RP', 'CP', 'ZM', 'RM', 'CM', 'VIN', 'LP', 'IT', 'VOUT']
STEP5: 回路方程式と未知数のシンボルリストを生成
start = 3
ind_eq = -1
ind_rt = 2
ce_sol = []
while True:
ind_eq = ce.find("=", ind_eq+1)
ind_rt = ce.find("\n", ind_rt+1)
if ind_rt == -1:
break
exec("ce_sol.append(" + ce[start:ind_eq] + "-(" + ce[ind_eq+1: ind_rt] + "))")
start=ind_rt + 1
exec("uk_sol = " + uk)
exec("wn_sol = " + wn)
以下のような処理をすることで方程式と未知数のシンボルリストを生成しています。
(i) STEP1にて回路方程式ceが入力される
ce:
ZP = RP / (1 + sCPRP)
ZM = RM / (1 + sCMRM)
VIN = (s*LP + ZP + ZM)*IT
VOUT = ZM * IT
(ii) ceからイコール'='と改行'\n'を見つけ、右辺を左辺に移項したリストを作成する
ce_sol:
-RP/(CPRPs + 1) + ZP,
-RM/(CMRMs + 1) + ZM,
-IT*(LPs + ZM + ZP) + VIN,
-ITZM + VOUT
(iii) 未知数(uk)と求めたい変数(wn)については以下のコードを実行する
uk_sol = ZP, ZM, IT, VOUT
wn_sol = VOUT
STEP6: 方程式を解いて整理する
ようやく方程式を解く部分です。
if len(uk_sol) != len(ce_sol):
print("未知数と方程式の数を揃えて下さい。")
else:
sol = solve(ce_sol, uk_sol, dict=True)[0][wn_sol]
# 分母分子を整理する
nu = collect(expand(numer(sol)), s) # Numerator、分子
de = collect(expand(denom(sol)), s) # denominator、分母
sol = nu / de
未知数と方程式の数が揃っていないと解は得られないので、最初にこれを確認しています。
方程式は以下のコードによって解かれます。
sol = solve(ce_sol, uk_sol, dict=True)[0][wn_sol]
solve(ce_sol, uk_sol, dict=True)を実行すると以下のように全ての未知数の解が得られますが、
[0][wn_sol]を追加することで求めたい解(今回はVOUT)だけを取り出しています。
_sol = solve(ce_sol, uk_sol, dict=True)を実行した結果:
ZP: RP/(CPRPs + 1)
ZM: RM/(CMRMs + 1)
IT: VIN*(CMRMs + 1)(CP~省略~
VOUT: RMVIN*(CPRPs + 1~省略~
解を求めたあとは分母分子をsについて整理しています。
求めた解は以下のように読みづらい状態です。
sol:
$$\displaystyle \frac{CP RM RP VIN s + RM VIN}{CM CP LP RM RP s^{3} + RM + RP + s^{2} \left(CM LP RM + CP LP RP\right) + s \left(CM RM RP + CP RM RP + LP\right)}$$
#式の表示
sol_tex = latex(sol)
for i in range(len(ce_sym)):
sol_tex = sol_tex.replace(latex(ce_sym[i]), ce_tex[i])
display(Math(sol_tex))
そこで方程式の表示を見やすくするために、TeX表示に変換しています。
例えばVOUTであればV_{OUT}に置換します。
最終的に得られる結果は以下の通りで、TeX表示にしたことで可読性が良くなりました。
$$\displaystyle \frac{C_{P} R_{M} R_{P} V_{IN} s + R_{M} V_{IN}}{C_{M} C_{P} L_{P} R_{M} R_{P} s^{3} + R_{M} + R_{P} + s^{2} \left(C_{M} L_{P} R_{M} + C_{P} L_{P} R_{P}\right) + s \left(C_{M} R_{M} R_{P} + C_{P} R_{M} R_{P} + L_{P}\right)}$$
#変数名
TeX表示をするために数式の置換を行っていますが、記号名によっては思わぬ動作をする可能性があります。
例えばacという記号を使用すると、TeXコードにおける\fr ac を置換してしまいます。
このため、記号は基本的に大文字から始めるようにして下さい。
おわりに
解説は以上です。ユーザーが入力するのは回路方程式と未知数、そして求めたい変数だけですので、必要最小限の労力で回路方程式が解けます。節約できた労力は、得られた結果の解釈に使うことが出来ます。たとえば、項の大小関係から式を簡単化することも出来るでしょう。
今回を回路方程式を人間が立てましたが、回路方程式を立てるのことすら面倒くさい(時間が無い)場合もあると思います。この場合、Lcapyというpythonパッケージを使うことで回路方程式を立てることも自動化できます。ユーザーが行うのは回路図を描くことだけです。これについての解説記事を書きましたので、ご興味を持たれた方は是非そちらもご覧ください。
【回路×Python】線形回路解析パッケージLcapyを使えるようにする方法
【回路×Python】Lcapyを使って回路の伝達関数を求める方法
【回路×Python】Lcapyを使って伝達関数を展開・計算する方法
-
BW1という記号を使った場合、Tex表示は$BW_1$にはならず、$B_{W1}$となってしまうため注意が必要です。 ↩