Quantopianには独自のリスク評価モデルが用意されていて、そのロジックがWhitepaperとしてサイトに上がっているので、備忘録的にざっくりとまとめていきます。
Abstract
リスクモデリングは投資戦略において、リスクの原因を理解し、処理するために重要です。Quantopianが独自に開発したQRM(Quantopian Risk Model)では、投資戦略を定量的に評価することが可能となります。以下では、そのロジックと実装について解説するという内容。
Introduction
リスクの定義について書かれています。当然と言えば当然ですが、投資において懸念されるリスクとはボラティリティの大きさです。ボラティリティの大きさは、損失とリターンの両方が平均値と離れて大きいことを指していると考えると、リスクを評価することで、リターンの期待値を合理的に予測することができるようになり、投資目標がどれだけの確率で達成されるかを測ることができます。また、リスクモデルを開発することで、リスク全体を「common risk」と「specific risk」に正しく分割できます。ここでいう「common risk」とは、企業財務やマクロ経済から得られる情報に基づく、株式市場内でリターンを押し上げる共通の要因に起因するリスクのことを指します。一方で、「specific risk」とは、これら「common risk」では説明しきれない要因として存在し、これらがQuantopianが定義する「アルファ」を推定するのに役立つようです。
Factor Models
じゃあどうやって因子を特定していけばいいの、という話ですが、ここでは従来用いられてきた3つの因子モデルについて説明しています。CAPM、ファーマ・フレンチの3ファクターモデル、裁定価格理論が紹介されていますが、ここらへんはググった方が早いので割愛します。
Implementation
ここでようやくQRMについての解説に入っていきます。QRMは以下の11個のセクター要因と5個のスタイル要因によって各資産のリターンを分解しようとするものです。
セクター要因
| SECTOR | SECTOR INDEX j | ETF | MORNINGSTAR-CODE |
|---|---|---|---|
| Materials | 1 | XRB | 101 - Basic Materials |
| Consumer Discretionary SPDR | 2 | XLY | 102 - Consumer Cyclical |
| Financials | 3 | XLF | 103 - Financial Services |
| Real Estate | 4 | IYR | 104 - Real Estate |
| Consumer Staples | 5 | XLP | 205 - Consumer Defensive |
| Healthcare | 6 | XLV | 206 - Healthcare |
| Utilities | 7 | XLU | 207 - Utilities |
| Telecom | 8 | IYZ | 308 - Communication Services |
| Energy | 9 | XLE | 309 - Energy |
| Industrials | 10 | XLI | 310 - Industrials |
| Technology | 11 | XLK | 311 - Technology |
スタイル要因
| STYLE FACTOR NAME | STYLE INDEX j |
|---|---|
| momentum | 1 |
| size | 2 |
| value | 3 |
| short-term reversal | 4 |
| volatility | 5 |
数式モデル
$$r_{i,t} = \sum_{j=1}^n\beta_{i,j,t}^{sect}f_{j,t}^{sect} + \sum_{k=1}^m\beta_{i,j,t}^{style}f_{j,t}^{style} + \epsilon_{i,t}$$
となっていますが、これはある日の各資産のリターンが、その資産が属するセクターと5つのスタイルによってどれだけ説明できるかを定量的に評価していて、それらで説明しきれない要因を残差としてεで表しています。Quantopianで用意されている各資産は必ず上記セクターの最低一つ以上に属しており、属していないセクターのβ値は0となります。
ここで、リターンがセクターのリターン、あるいはスタイルのリターンに大きく依存しているとすると、リスク評価の観点でポートフォリオとしてはあまり優れていないということになります。
スタイル要因の定義
| STYLE FACTOR | Definition |
|---|---|
| momentum | 上向きスイングの株(勝者株)と下向きスイングの株(敗者株)の11ヵ月後のリターンの差 |
| size | 大型株と小型株のリターンの差 |
| value | 安価な株と高価な株の間のリターンの差 |
| short-term reversal | 高ボラティリティ株式と低ボラティリティ株式のリターンの差 |
| volatility | 理論的に反転する直前の、最近の損失の強い株式と、理論的に反転する直前の、最近の利益の強い株との間のリターンの差 |
| 各スタイル要因の数学的定義は公式ドキュメントに記載されていますが、長くなりそうなのでここではこういう風に計算するんだーくらいでに思ってもらえればいいと思います(適当ですみません)。 |
Methodology
先ほどQRMの数式モデルについて説明しましたが、正確には、最初にファクター要因を説明変数にして回帰分析を行い、そこで得られた残差収益を目的変数にして、再び回帰分析を行うことで、スタイル要因のβ値を算出します。
ここでは、実際にセクター要因の計算、スタイル要因の計算をどのように行なっているかを説明しています。
セクター要因の計算モデル
各資産の2年間の株価収益率と、その資産が属するセクターの収益率を使用して、各資産がどれだけセクター要因に依存しているかを推定します。
例えば、アップル株を扱う場合、
- アップルのモーニングスターコードを調べる。アップルはTechnologyセクターに属するため、ここではXLKが選ばれる。
- ベクトルfにXLKセクターの2010/12/31から2013/1/2までの毎日の収益率が格納される。
- ベクトル$r_i$にアップル株の2010/12/31から2013/1/2までの毎日の収益率が格納される。
- $r_i$とfで回帰分析をした結果、推定されたβが、アップル株の収益率がTechnologyセクター要因によってどれだけ説明されるかを表すことになる。
- 列ベクトル$ε_i^{sect}$は、過去2年間でセクター要因によって説明しきれなかった残差として表される。
スタイル要因の計算モデル
各スタイル要因の収益率を計算する上では、「普通株である」・「十分なデータ量を持っている」・「流動性が高い」という3つの基準を満たした銘柄のみを使用しているようです。これらの銘柄は「estimation universe」として定義され、この範囲外から外れた銘柄を「complementary stocks」呼んでいます。
ここでは、「estimation universe」の銘柄のスタイル要因の説明係数と収益率の計算方法、および「complementary stocks」のスタイル要因の説明係数の計算方法を解説しています。
「estimation universe」のスタイル要因の説明係数の導出
ある日の各銘柄のスタイル要因のエクスポージャーは、その日の各銘柄のスタイル要因を標準化することで与えられています。この標準化は、estimation universeの全銘柄を範囲として行われているようです。以下では、こうして導出されたスタイル要因のエクスポージャーを所与として収益率の計算を行います。
スタイル要因の収益率の導出
- 上記で導出したスタイル要因のエクスポージャーを、B行列のカラムに格納する。(行数5、列数tの行列になる)
- セクター要因の分析で出た、ある日のセクター要因の残差をベクトル$ε_t^{sect}$に格納する。(行数tの列ベクトルになる)
- 列ベクトル$ε_t^{sect}$をB行列の各カラムで回帰分析する。
- それぞれの回帰係数($f_{1,t}^{style},f_{2,t}^{style},f_{3,t}^{style},f_{4,t}^{style},f_{5,t}^{style}$)から5つのスタイル要因についての収益率が得られる。
- 4で得た5つの収益率を列ベクトル$f_k^{style}$としてまとめる。
- 2の列ベクトル$ε$から$\sum_{k=1}^5B_{:k}f_{k,t}^{style}$を引くことによって、残差収益率$ε_t^{style}$を算出する。
「complementary universe」のスタイル要因の説明係数の導出
スタイル要因の収益率と、セクター要因の残差との多重線形回帰分析で算出。基本的には変わらないので省略。
リスク計算
最初の話に戻ってくるが、資産iの抱えるリスクは平均収益からの乖離幅で表されるよということで、
$$\sigma = {\sqrt{{1 \over T} {\sum_{l=1}^r} (r_l - \bar{r}_i)^2 }}$$
これに各変数を代入して、
$${\sqrt{{1 \over T} {\sum_{l=1}^T} (\beta_{i,k,t}^{style} f_{k,l}^{style} - \overline{\beta_k^{style} f_k^{style}} )^2 }}$$
本題
本題というかなんというか、前回の記事で作ってみたアルゴリズムの各要因の収益とリスクエクスポージャーを見てみる。
bt = get_backtest('5c49773b3c83724b4635cffe')
bt.create_perf_attrib_tear_sheet()
バックテストで得られたbacktest_idをはめ込んで、tear_sheetを作る。
backtest_idは、フルバックテストを実行した画面のhttps://www.quantopian.com/algorithms/~~/○○の○○の部分です。
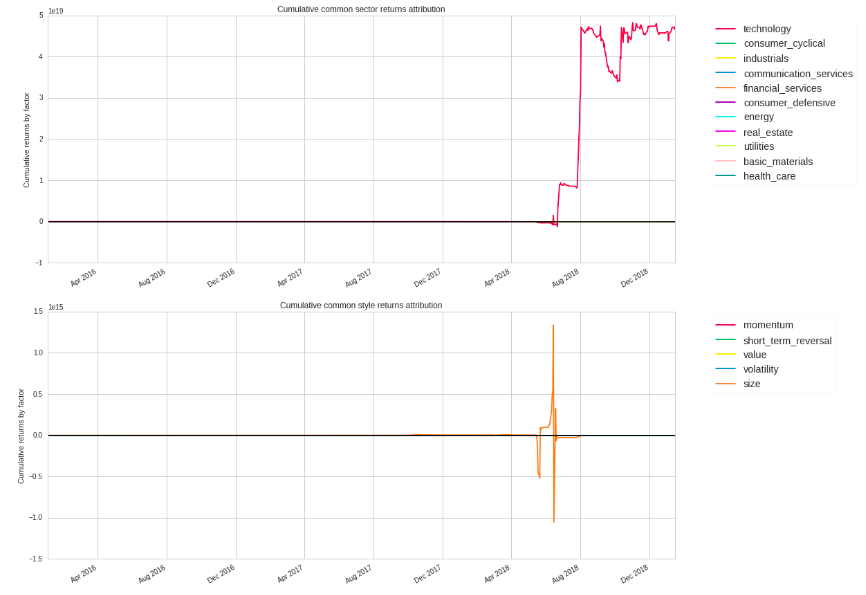
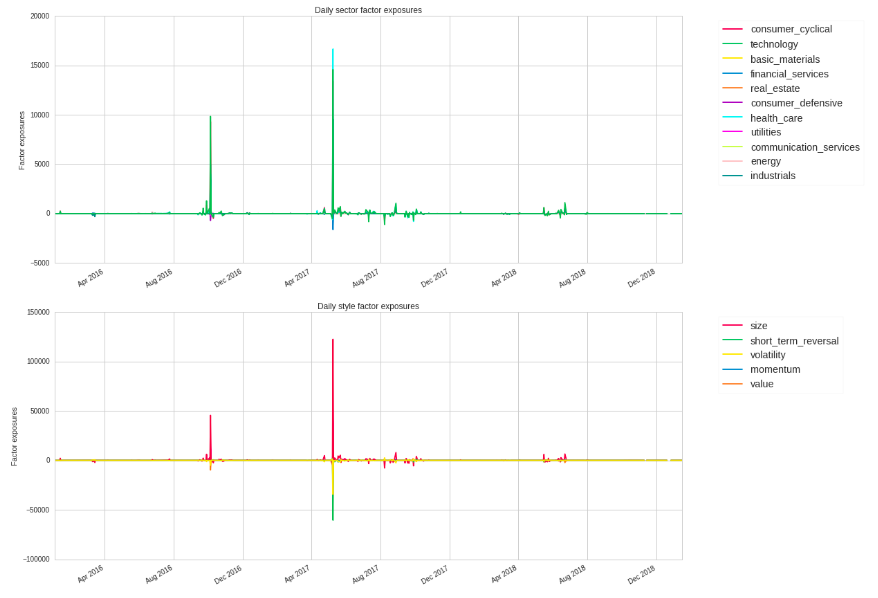
収益が特定のセクター、スタイル要因に偏っていることがわかりますね。
リスク要因から見て僕のアルゴリズムのパフォーマンスはあんまり良くないようです。
まとめ
理論的にはなんとな〜くわかったので、じゃあリスクエクスポージャーを小さくするアルゴリズムを作るには実際にどうすればいいんだという部分をまとめていければなあと。