はじめに
12/28~30 PythonBootCamp内で作成した関数を少しブラッシュアップして記事にしました。
コラッツの問題 Collatz problem とは
コラッツの問題は非常に単純な問題ながら、いまだ自然数 n に対しての証明がなされていない。
2の68乗まではコンピューターで計算をして正しいことは確認ができているらしい。
任意の正の整数 n をとり、
n が偶数の場合、n を 2 で割る
n が奇数の場合、n に 3 をかけて 1 を足す
という操作を繰り返すと、どうなるか
というものである。「どんな初期値から始めても、有限回の操作のうちに必ず 1 に到達する(そして 1→4→2→1 というループに入る)」という主張が、コラッツの予想である。
正確な定義などはWikipediaを参照してください。
コラッツの問題(コラッツのもんだい、Collatz problem)は、数論の未解決問題のひとつである。1937年にローター・コラッツが問題を提示した。問題の結論の予想を指してコラッツの予想と言う。固有名詞に依拠しない表現としては3n+1問題とも言われ、初期にこの問題に取り組んだ研究者の名を冠して、角谷の問題、米田の予想、ウラムの予想、他にはSyracuse問題などとも呼ばれる。数学者ポール・エルデシュは「数学はまだこの種の問題に対する用意ができていない」と述べ、解決した人に500ドルを提供すると申し出た。 ジェフリー・ラガリアスは2010年に、コラッツの予想は「非常に難しい問題であり、現代の数学では完全に手が届かない」と述べた。
コンピュータを用いた計算により、2の68乗までには反例がないことが確かめられている。 また、2011年度大学入試センター試験数学IIB第6問に題材として取り上げられた。
コラッツの問題を描画する Plotly.express で
import plotly.graph_objects as go
import plotly.express as px
def collatz(num):
n = num
k = 0 # 引数を変数に格納。
lst = [n] # リストを準備 引数を最初に入れておく。
while n > 1: # While文をまわす。1になったら終了。
if n % 2 == 0: # 偶数・奇数を判定
n = n /2
lst.append(int(n))
k += 1 # 計算が1回終わったらリストに格納していく。
elif n % 2 == 1:
n = n * 3 + 1
lst.append(int(n))
k += 1
print("試行回数:",k)
fig = px.line(y=lst,)
fig.update_layout(title="コラッツ問題をPlotlyで描画してみる",
width=1000,
height=400,
template="plotly_dark",
font={
"family":"Meiryo",
"size":10
}
)
fig.update_xaxes(title_text='試行回数')
fig.update_yaxes(title_text='数値')
fig.show()
print(lst)
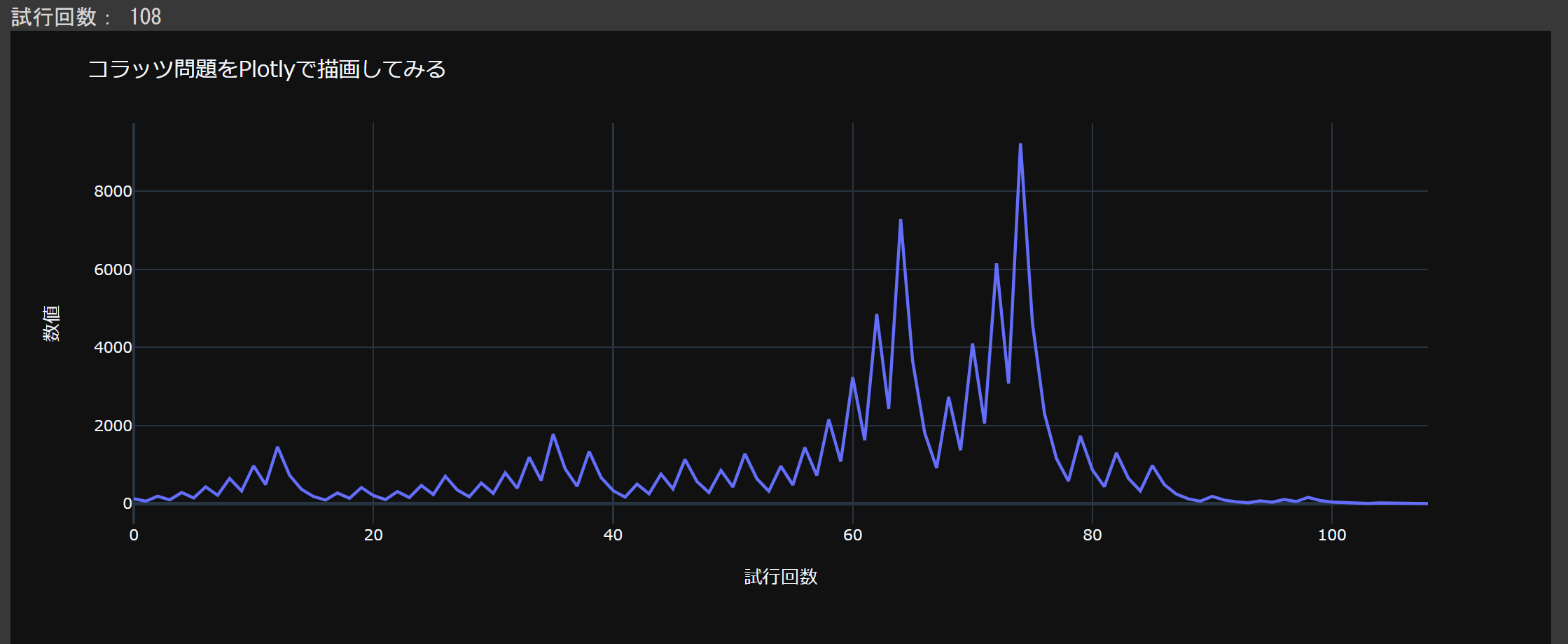
python collatz(126)
126をコラッツの問題の通り数字を計算していくと、最大値 9232 を通り、計算108回行うと最後は1に収束していきます。
指定数間の試行回数を描画する
import pandas as pd
def collatz_num(n, m):
lst = list(range(n,m+1))
k_lst = []
for i in lst:
k = 0
while i > 1:
if i % 2 == 0:
i = i / 2
k += 1
elif i % 2 == 1:
i = i * 3 + 1
k += 1
k_lst.append(k)
df = pd.DataFrame(k_lst, columns=["試行回数"])
df["指定数"] = lst
print("試行回数 最大値:",df["試行回数"].max())
fig = px.line(y = k_lst, x = lst)
fig.update_layout(title="必要試行数",
width=1000,
height=400,
template="plotly_dark",
font={
"family":"Meiryo",
"size":10
}
)
fig.update_xaxes(title_text='指定数')
fig.update_yaxes(title_text='試行回数')
fig.show()
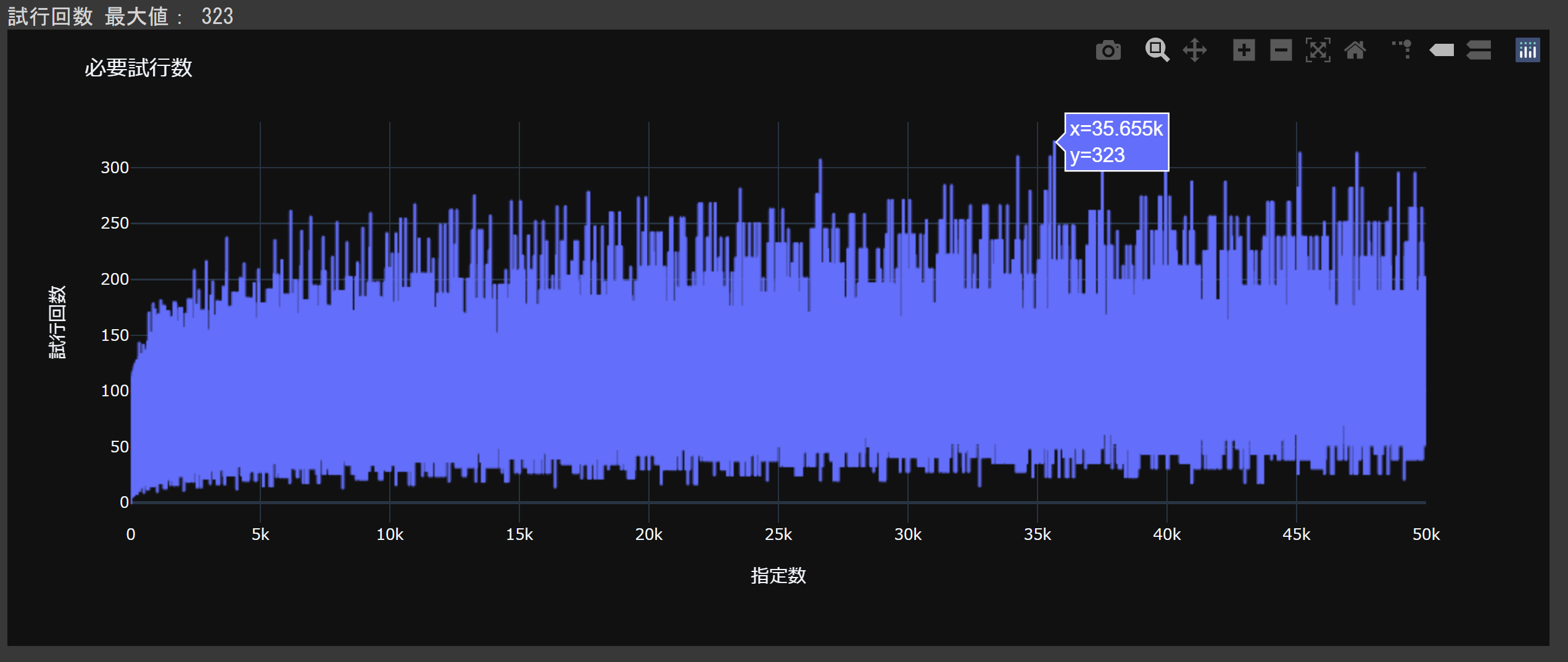
python collatz_num(1, 50000)
初期値が大きければ試行回数が増えていくわけでもない。
1~50,000の間では、x = 35,655 で試行回数がMAXになることがわかる。
確認をする
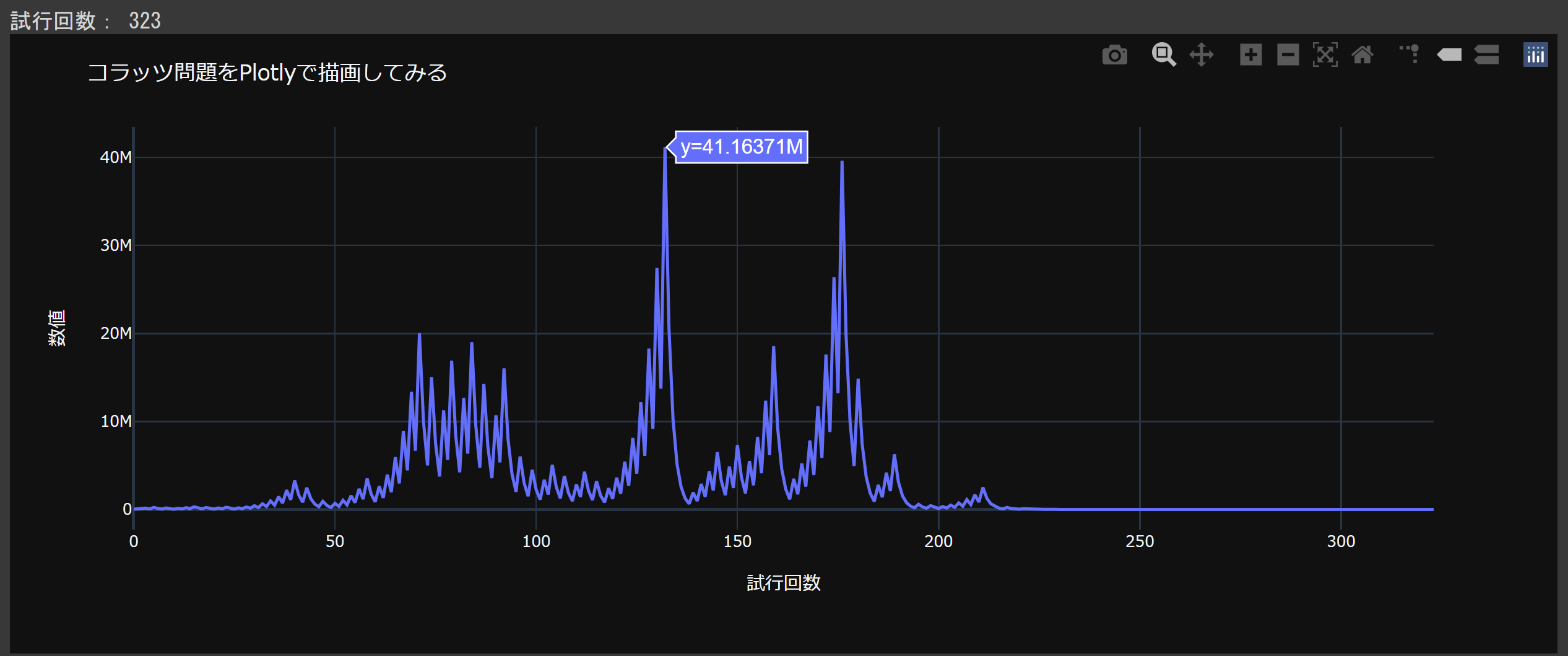
collatz(35655)
35,000台ではじまった計算がとちゅうで 410,000超 まで増加していることがわかる。
その後一気に減ったかと思うとまた400,000に迫るところまで数を増やしながら、最終的にはもちろん1に収束。
こどもと遊ぶ
我が家では、小6・小3の子どもに紙とえんぴつを渡し、下記の数値で計算をしてみました。
親 初期値 128 試行回数 7回
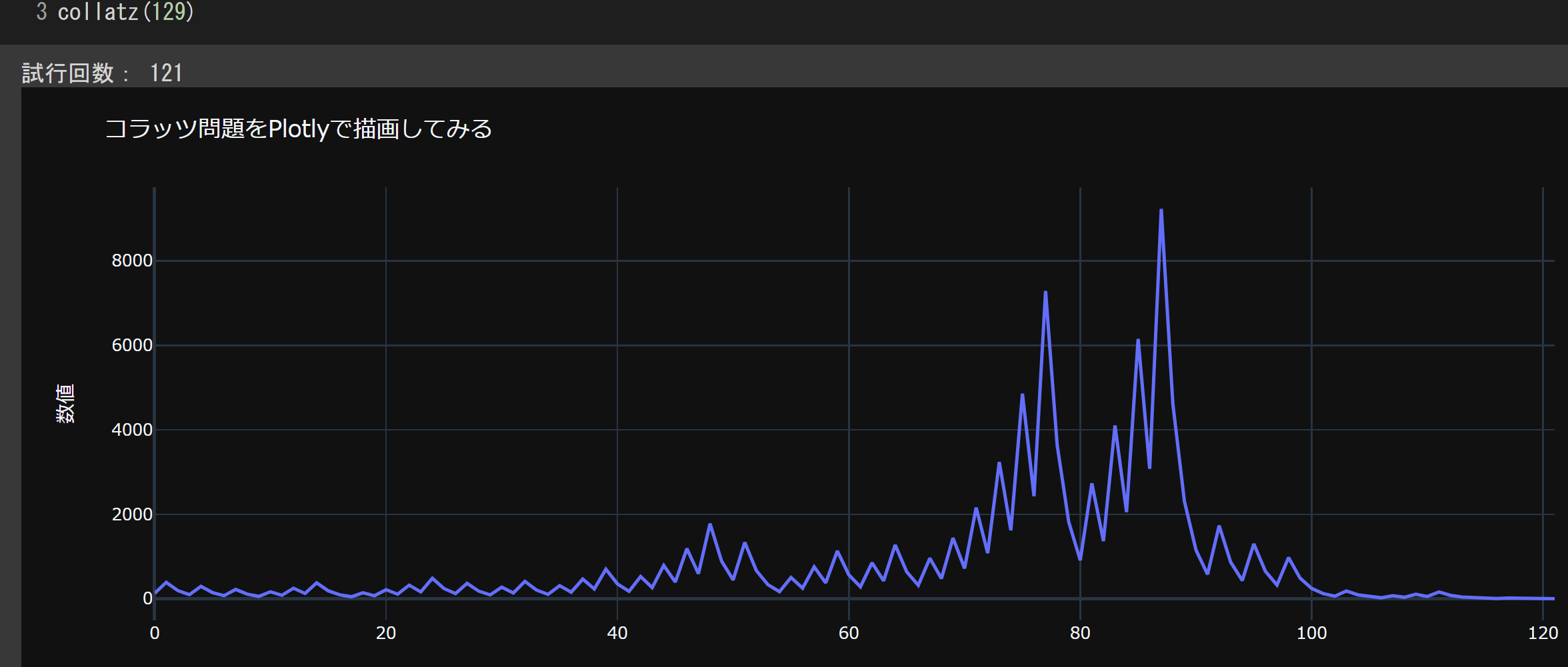
子 初期値 129 試行回数 121回
速攻計算が終わる親。
初期値129からはじまったのに、途中で1万に迫る数になりビビる子ども。
紙とえんぴつでなんとか計算しきりました。なんだかんだ盛り上がりました。
懸賞金ついてます!
解いたら1億2千万円!