こんにちはsoheiです![]()
今回はこの迷路を題材に幅優先探索と深さ優先探索を使いpythonで解いていきたいと思います。
アルゴリズムを学習するのは今回が初めてなので、色々と間違っているところがあると思いますが、どうかご了承ください![]()
今回題材にする迷路はこちらです。
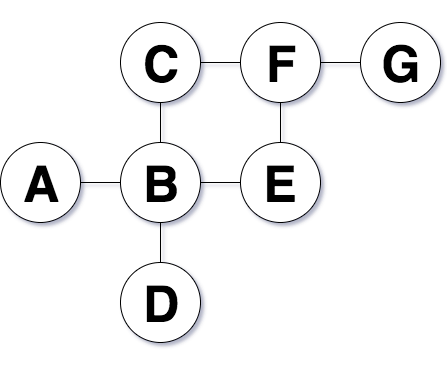
今回はここのAを開始地点とし、Gをゴールにしたいと思います。
入力
まず迷路の縦と横の長さが与えられ、その後迷路が与えられることとします
ex)
3 4
# E F G
A B D #
# C # #
出力
ここでの出力は、スタートからゴールまでの距離とゴールに行き着くまでの処理の回数とします。
ex)
ゴールまでの距離は4
かかった処理の回数は4
幅優先探索
流れ
①迷路を読み込む
②Queueの中に開始地点AをQueueに入れる
③取り出す
④ゴールか判定
⑤チェック済みリストに入れる
⑥隣接しているものをQueueに入れる
⑦③に戻る
実装
# -*- coding: utf-8 -*-
import math
h,w = map(int, raw_input().split())
lst = [] #迷路
queue = ["A"] #キュー!
check = ["A"] #チェック済みリスト
count = 0 #処理のの回数を数える
for i in range(h):
x = map(str,raw_input().split())
lst.append(x) #迷路の読み込み
for j in range(h):
if "A" in lst[j]:
hNow, wNow = j, lst[j].index("A") #開始地点Aの位置の読み込み
hNow2, wNow2 = hNow, wNow
while 1:
count += 1
for k in range(h):
if queue[0] in lst[k]:
hNow, wNow = k,lst[k].index(queue[0]) #取り出す
if len(queue) != 0:
if queue[0] == "G":
break # ゴールか判定
queue.pop(0)
if hNow < h-1:
if lst[hNow+1][wNow] != "#":
if lst[hNow+1][wNow] not in check:
queue.extend(lst[hNow+1][wNow])
check.append(lst[hNow+1][wNow])
if wNow < w-1:
if lst[hNow][wNow+1] != "#":
if lst[hNow][wNow+1] not in check:
queue.extend(lst[hNow][wNow+1])
check.append(lst[hNow][wNow+1])
if hNow > 0:
if lst[hNow-1][wNow] != "#":
if lst[hNow-1][wNow] not in check:
queue.extend(lst[hNow-1][wNow])
check.append(lst[hNow-1][wNow])
if wNow > 0:
if lst[hNow][wNow-1] != "#":
if lst[hNow][wNow-1] not in check:
queue.extend(lst[hNow][wNow-1])
check.append(lst[hNow][wNow-1]) #近いやつを入れる
print "ゴールまでの距離は"+str(abs(hNow - hNow2) + abs(wNow - wNow2))
print "かかった処理の回数は"+str(count)
実行結果
ゴールまでの距離は4
かかった処理の回数は7
深さ優先探索
流れ
幅優先と同じ(ただしqueueをスタックにする)
実装
# -*- coding: utf-8 -*-
import math
h,w = map(int, raw_input().split())
lst = [] #迷路
stack = ["A"] #スタッック!
check = ["A"] #チェック済みリスト
count = 0 #処理の回数を数える
for i in range(h):
x = map(str,raw_input().split())
lst.append(x)
for j in range(h):
if "A" in lst[j]:
hNow, wNow = j, lst[j].index("A")
hNow2, wNow2 = hNow, wNow
while 1:
count += 1
for k in range(h):
if stack[-1] in lst[k]:
hNow, wNow = k,lst[k].index(stack[-1]) #取り出す
if len(stack) != 0:
if stack[-1] == "G":
break #ゴールか判定
stack.pop()
if hNow < h-1:
if lst[hNow+1][wNow] != "#":
if lst[hNow+1][wNow] not in check:
stack.extend(lst[hNow+1][wNow])
check.append(lst[hNow+1][wNow])
if wNow < w-1:
if lst[hNow][wNow+1] != "#":
if lst[hNow][wNow+1] not in check:
stack.extend(lst[hNow][wNow+1])
check.append(lst[hNow][wNow+1])
if hNow > 0:
if lst[hNow-1][wNow] != "#":
if lst[hNow-1][wNow] not in check:
stack.extend(lst[hNow-1][wNow])
check.append(lst[hNow-1][wNow])
if wNow > 0:
if lst[hNow][wNow-1] != "#":
if lst[hNow][wNow-1] not in check:
stack.extend(lst[hNow][wNow-1])
check.append(lst[hNow][wNow-1]) #近いやつを入れる
print "ゴールまでの距離は"+str(abs(hNow - hNow2) + abs(wNow - wNow2))
print "かかった処理の回数は"+str(count)
実行結果
ゴールまでの距離は4
かかった処理の回数は4
学んだ知識
・多次元配列について
・アルゴリズムについて
考察
今回の学習で学んだことは、アルゴリズムに限らず、プログラミングは書き方は何百通りもあり例えば、僕の場合は、for文やif文を使って書きましたが、ある人は関数を使って書いたり、はたまたいろいろな省略の方法を使って10行ほどで仕上げる人もいたりと個性が出るということです。またそれと同時に、プログラミングをする身において、その何百通の中から『最速』『最短』というものが求められるということも学びました。どんどん便利になっていく世の中にとって、『最速』『最短』という言葉は、今後キーワードになっていくと思います。そのためにはもっとプログラミングを学ばないとですね![]()
今回はここら辺で失礼します。次回は幅優先、深さ優先の練習問題をときたいと思います。
間違っているところなどありましたら、コメントお願いします。
それでは次の記事で会いましょう![]()
編集後記
幅優先と深さ優先を理解したあなたはこの問題を解くことをお勧めします。
http://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=1130&lang=jp
pythonでの解き方はこちらです