はじめに
こんにちは。犬です。
犬でもわかった気になれたので、RSAについて書きます。
RSAとは
よく使われる公開鍵暗号方式の一つです。
(公開鍵暗号方式については、下の方に書いてますので安心してください)
Wikipediaには以下のように書かれてます。
RSA暗号とは、桁数が大きい合成数の素因数分解問題が困難であることを安全性の根拠とした公開鍵暗号の一つである。
要するに素因数分解すれば解けるが、すごいコンピュータを使ってもすごい時間がかかるので、少なくとも生きてる間は安全ということらしいです。
RSA暗号は鍵長が1024bit未満でも、「スーパーコンピュータで640個のノードすべてを使用した場合でもキーデータを見つけるのに10年ほどかかる」らしいです。
現在推奨されているのが2048bit以上と考えると、とても生きている時間に解けるとは思いませんね。 ※1
前提知識
公開鍵
他人に見せてよい鍵。
この鍵で平文を暗号を作ります(暗号化)。
秘密鍵
他人に見せては行けない鍵。
この鍵で暗号文をもとに平文を作ります(復号)。
公開鍵暗号
公開鍵で暗号化した暗号文は、秘密鍵で復号できるという性質があります。
(そういう性質を持つように作られているのです。※2)
その性質を使って、以下の手順で暗号をやり取りします。
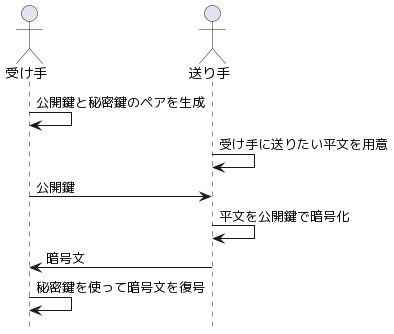
手順
暗号文の送り手と受け手と使って説明します。
1. 鍵ペアの作成
公開鍵と秘密鍵を受け手が作成します。
秘密鍵は厳重に管理し、公開鍵は誰でも見えるようにします。
2. 暗号化
送り手が公開されている受け手の公開鍵を取ってきて、
その鍵をもとに平文(暗号化したい文章)を暗号化します。
3. 送信
暗号文を送信します。
4. 復号
受け手が暗号文を受け取って、
秘密鍵を用いて復号を行い、平文を取り出します。
手順
まずは何も考えず手順を追ってみましょう。
(今回使用する値はすべて自然数です。)
鍵ペアの作成
以下の手順で受け手が公開鍵と秘密鍵を求めます。
求めた公開鍵は送り手に渡します。
1. 二つの大きな素数を用意する
適当に大きい素数である $P$ と $Q$ を用意します。
(本来はここでランダムに大きな素数を取り出します。)
例
P = 17, \quad Q = 13
コード例(Python)
P = 17
Q = 13
2.公開鍵1を求める
上記の素数の積を公開鍵$N$と置きます。
$$N = P \times Q$$
計算例
$$N = P \times Q = 17 \times 13 = 221$$
コード例(Python)
N = P * Q
3. Lを計算する
互いに素
$N$との最大公約数が1になる数を$N$と互いに素である数といいます。
例を上げるなら$5$と$7$は互いに素ですし、$3$と$6$は互いに素ではないです。
オイラー関数
今回は$N$より小さい、$N$と互いに素である数字の数$L$を調べます。
このときの数字の数を$\phi(N)$とも表記します。
(オイラー関数と言うやつです。)
$$L = \phi(N)$$
例えば$T = 6$の場合、$T$より小さくて$T$との最大公約数が1になる数字は、
$1$と$5$があるので、$\phi(T) = 2$となります。
二つの素数の積を引数としたオイラー関数
素数である$P$と$Q$は互いに素なのですが、
$P$と$Q$が互いに素であるとき、
$\phi(P \times Q)$ = $(P-1) \times (Q-1)$であることが知られています。
実践・計算
もう一度いいますが、今回は$N$より小さい$N$と素である数字の数$ L(=\phi(N))$ を求めます。
$N = P \times Q$ですので、
$$L = \phi(N) = \phi(P \times Q) = (P-1)\times(Q-1)$$
となります。
計算例
\begin{align}
P &= 13, \quad Q = 17 \\
\\
L &= \phi(N) \\
&= (P-1)\times (Q-1) \\
&= (17-1)\times(13-1) \\
&= 16 \times 12 = 192
\end{align}
コード例(Python)
L = (P-1) * (Q-1)
4. 公開鍵2を決める
条件
公開鍵$E$は以下の条件を満たさないといけません。
- $1$より大きく、$L$より小さい
- $L$と互いに素である
(つまり$E$と$L$の最大公約数が$1$)
決める例
$L = 192$のとき、
$E = 5$は公開鍵として選ぶことができます。
($E$として選べる数字はいくつもありますが、
今回は$5$を選びます。)
- $1 < 5 < 192$がなりたつ
- $5$と$192$は互いに素である
(つまり$5$と$192$の最大公約数が$1$)
※3
コード例(Python)
'''
Eとして選べる数字はいくつもあるが、
今回は一番小さいものを選んでいる
'''
for E in range(2, L):
if math.gcd(E, L) == 1:
break
5. 秘密鍵を決める
条件
公開鍵$D$は以下の条件を満たさないといけません。
- $E \times D = L \times n + 1 \quad(nは任意の整数)$
- 式を変形すると、$E \times D \bmod L = 1$
つまり$E \times D$を$L$で割ったあまりが$1$である。
- 式を変形すると、$E \times D \bmod L = 1$
- $1$より大きく、$L$より小さい
計算例
$L = 192, \quad E = 5$のとき、
秘密鍵$D$として$77$が成り立ちます。
- $5 \times 77 \div 192 = 2 ... 1$
※3
コード例(Python)
for D in range(2, L):
if (E * D) % L == 1:
break
暗号化
以下の操作は送り手が受け手から受け取った、
公開鍵($N$と$E$)をもとに行います。
6. 暗号化
暗号文$C$は、$M$を$E$乗したものを$N$で割った余りとなります。
$$ C = M^E \bmod N $$
計算例
\begin{align}
N &= 221 \\
E &= 5 \\
M &= 11\\
C &= 11^5 \bmod 221 \\
&= 163
\end{align}
コード例
# 公開鍵N、公開鍵Eは
# 受け手からもらったものを使う
N = 221
E = 5
# 平文Mを用意
M = 11
# 暗号化
C = M ** E % N
print(f'暗号文 C = {C}')
復号
以下の操作は受け手が送り手から受け取った、
暗号文$C$と受け手が持っていた秘密鍵$D$、公開鍵$N$を使って復号を行います。
7. 復号
平文$M$は$C$を$D$乗したものを$N$で割った余りとなります。
$$M = C^D \bmod N$$
計算例
\begin{align}
C &= 163 \\
N &= 221 \\
D &= 77 \\
M &= 163^{77}\bmod{221}\\
&= 11
\end{align}
コード例
# 暗号文Cは
# 送り手からもらっている
C = 163
# 公開鍵N、秘密鍵Dは
# 既に計算したものを使う
N = 221
D = 77
# 復号
M = C ** D % N
print(f'平文(復号後) M = {M}')
安全性について
機密でない情報は、公開鍵$E$、$N$と暗号文$C$です。
これらを使って平文$M$、または$D$を求めることができれば、この暗号が危険といえます。
Mを求める
$M = C^D \bmod N$より、平文$M$を求めるためには暗号鍵$D$が必要です。
Dを求める
二つの大きな素数$P$と$Q$が分かれば、$P$と$Q$と公開鍵$E$をもとに、
鍵ペア作成と同じ手順で暗号鍵$D$が計算できます。
PまたはQ求める
$N = P \times Q$なので、二つの大きな素数$P$と$Q$は公開鍵$N$を素因数分解することで求められます。
しかし、あまりにも$P$と$Q$が大きいため、計算時間上困難です。
まとめ
今回は名前は知っているけど、仕組みはわかってないことが多い、RSAの仕組みについて解説しました。
このような仕組みによって、世の中の通信の安全性が保たれていると思うと、なんだかおもしろいですね。
以下に今回使った数式、処理、コード等についてまとめてあるので、ぜひ使ってください。
値
| 名前 | 式 | 意味 | 例 | 機密情報であるか |
|---|---|---|---|---|
| $P$ | - | 大きな素数 | $17$ | Yes |
| $Q$ | - | 大きな素数 | $13$ | Yes |
| $N$ | $N = P \times Q$ | 公開鍵1 | $17 \times 13 = 221$ | No |
| $L$ | $L=\phi(N) = (P-1) \times (Q-1)$ | $N$より小さい、$N$と互いに素である数字の数 | $(17-1)\times(13-1) = 192$ | Yes |
| $E$ | $1 < E < L,\quad gcd(E, L) = 1$ | 公開鍵2 | $5$ | No |
| $D$ | $E \times D = 1 + L$を満たす$D$ | 復号鍵 | $77$ | Yes |
| $M$ | $M = C^D \bmod N$(復号) | 平文 | $11$ | Yes |
| $C$ | $C = M^E \bmod N$(暗号化) | 暗号文 | $163$ | No |
処理
| 名前 | 処理 | 意味 |
|---|---|---|
| 暗号化処理 | $C = M^E \bmod N$ | $M$を暗号化した$C$を計算する |
| 復号処理 | $M = C^D \bmod N$ | $C$を復号した$M$を計算する |
コード
Pythonのコードはまとめると以下のようになります。
import math
print("-- 鍵ペア生成 --")
# 大きな素数PとQ
P = 17
Q = 13
print(f'大きな素数 P={P}, Q={Q}')
# 公開鍵Nの値を計算
# N = 221
N = P * Q
print(f'公開鍵 N = {N}')
# Lの値を計算
# L = 192
L = (P-1) * (Q-1)
# 公開鍵Eの値を決める
# E = 5
for E in range(2, L):
if math.gcd(E, L) == 1:
break
print(f'公開鍵 E = {E}')
# 秘密鍵Dの値を計算
# D = 77
for D in range(2, L):
if (E * D) % L == 1:
break
print(f'秘密鍵 D = {D}')
print("-- 暗号化 --")
# 平文M
# M = 11
M = 11
print(f'平文 M = {M}')
# 暗号文Cを計算
# C = 163
C = M ** E % N
print(f'暗号文 C = {C}')
print("-- 復号 --")
# 平文Mを計算
# M = 11
M = C ** D % N
print(f'平文(復号後) M = {M}')
備考
※1 サマーウォーズのケンジ君はこれを解きます。すごいですね。
※2 そういうように秘密鍵と公開鍵を作るのがRSAの仕事です。
※3 本当はもっとうまい方法で、計算しているのですが今回は説明しません。気が向いたら書くかもです。