こんにちは!アクセスありがとうございます。今回紹介する論文はこちらです。
日本語訳メインにちょくちょく解説いれます。
abst
この論文では、高度なグラフ構造情報、具体的には、ノードのペアの近傍が構造的にどのように関連しているかを測定する離散グラフ曲率を組み込んだ、新しいネットワークアーキテクチャが提案されています。エッジ$(x,y)$の曲率は、xの近傍からyの近傍までの移動距離をエッジ$(x,y)$の長さと比較することで定義されます。これは、ノード固有の属性または次数などの限られたグラフトポロジ情報にのみ焦点を当てていた以前のものと比較して、はるかに記述的な構造的測定:descriptive structural measureです。この曲率グラフたたみ込みネットワークは、さまざまな合成グラフと実際のグラフ、特に大きくて密度の高いグラフに対して、最先端の方法よりも優れています。
まあ、簡単に言えばノードの近傍が似ているかどうかを測る「曲率」を組み込んだ曲率グラフ畳み込みネットワークが特定の条件かでは既存のGCNとかより優れてるよって話です。
INTRODUCTION
近年DNNが成功を収めていますが、グラフ構造データに対しては有効ではありませんでした。しかし、近年のグラフ構造データ用の手法が次々と提案されています。
これらの手法は、畳み込みがスペクトル領域に適用されるか空間領域に適用されるかに応じて、大きく以下の2つのカテゴリに分類できます。
①スペクトルアプローチ
固有分解グラフラプラシアンに畳み込みを適用し、一般に計算とメモリの両方で効率的です。ただし、学習した畳み込みフィルターはグラフ固有であり、異なるグラフに一般化することはできません。
②スペーシャルアプローチ
空間的アプローチは、グラフ上で直接「畳み込み」を実行し、グラフトポロジで定義されているように近傍で動作します。
空間メソッドは、隣接ノードからの表現を集約することにより、各グラフノードの表現を繰り返し更新します。非線形変換は、メッセージと呼ばれる、あるノードから別のノードに渡される表現に適用されます。これらの変換は、同じ入力/出力次元、つまりノード表現の次元を持っています。それらは、異なるノード、さらには異なるグラフで共有および学習できます。
スペーシャルアプローチでは、グラフの局所的な構造情報を組み込むことが重要です。ノード次数は、メッセージの非線形変換を再パラメーター化するために、または追加のノード特徴量として使用されています。ただし、ノードの次数にはかなり制限があります。同じ次数分布の異なるグラフトポロジが存在する可能性があります。それがこちら。

ノード$x$と$y$は、3つの大きく異なるグラフ(木、格子、クリーク)で同じ次数を持っています。グラフ構造の知識を効果的に利用するには、これら3つを区別できるような特徴量が必要です。
上記をモチベーションに**この論文では、高度な構造情報を利用する新しいグラフニューラルネットワークが提案されました。**ノードの次数は、各ノードの隣接ノードの数を表すだけであり、これらの隣接ノードが相互にどのように接続されているかについては示しきれません。一対のノードの近傍が互いにどのように関連しているかを特徴付ける構造情報を使用します。図1では、$x$と$y$の近傍は、木の異なる枝で十分に分離されています。格子状グラフでは、2つの近傍は互いに平行シフトの範囲内にあります。クリークでは、それらは完全に重なり合っています。そのようなペアごとの構造情報を定量化するために、グラフの曲率に関する最近の研究(Ollivier、2009; Lin et al。、2011; Weber et al。、2016)を利用します。
離散グラフの曲率にはどのような意味が?
離散グラフの曲率(CURVATURE)は、近傍のペアのジオメトリ(形状)が「フラット」なケース、つまり格子グラフのケースからどの程度逸脱するかを測定します。グラフの離散曲率にはいくつかの定義があります。ここでオリビエのリッチ曲率を紹介します(Ollivier、2009)。この定義では無限格子グラフのエッジの曲率は$0$です。木のエッジの曲率は負であり、完全グラフでは正です。直感的に、**グラフの曲率は、2つの近傍がどれだけ適切に接続されているか、または互いに重なり合っているかを測定します。**このような情報は、情報が近隣でどのように伝播するかに関連しており、グラフたたみ込みネットワークで活用するできれば面白いという感じらしいです。
CURVATURE GRAPH NETWORK
最初にノードラベル予測問題を定式化し、グラフニューラルネットワーク(GNN)のメカニズムを説明します。
頂点に$H =(h_1,h_2,・・・,h_n),h_i∈R^F$の特徴を持つ無向グラフ$G =(V、E)$があるとします。ここで$n = |V|$はグラフのノード数で、$F$は各ノードの特徴の次元です。 $V$のノードのラベルがいくつか与えられ、残りのノードのラベルを予測します。 GNNはグラフ$G$のノード表現を繰り返し更新し、最終的にノードラベルを予測します。 GNNは、ノード表現を下位レベルのノード表現$H^t∈R^{n×F^t}$から更新する複数の隠れ層で構成されます。ここで、$F^t$は$t$番目のレイヤーにおける、上位レベルの表現$H^{t + 1}∈R ^{n×F^{t+1}}$に対しての特徴の次元です。 特に、$H^0$は入力$H$であり、$F^t = F$です。最後のノード表現&H^T&は、完全に接続されたレイヤーまたは線形分類器に供給され、ノードラベルを予測します。レイヤーとノードの表現をfig 2の上部に示します。
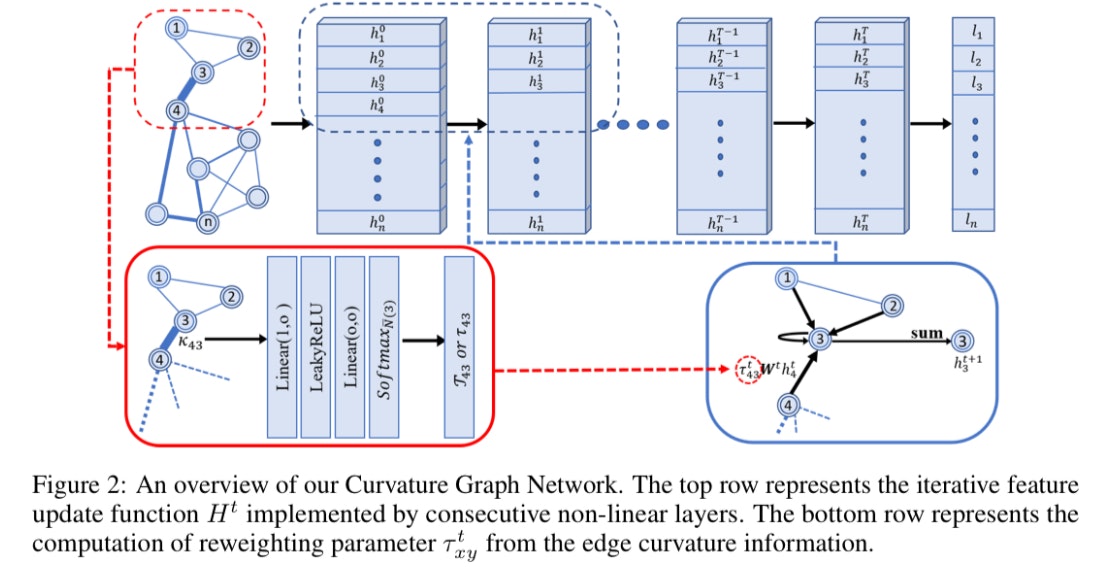
次に、ノード表現を$H^t$から$H^{t + 1}$に更新する隠れ層を構築する方法について説明します。スペーシャルアプローチに焦点を当て、畳み込みをメッセージパッシング方式として扱います。ノード$x$の$(t + 1)$番目の表現は、$x$の隣接ノードから渡されたメッセージを集約することによって計算されます。 Xから自信へのメッセージも含まれます。平均、最大、合計など、いくつか集計方法が存在します。この論文では、一般的ということでsumが使われていました。
$\overline{N(x)}= N(x)∪{x}$で、それ自体を含むxの近傍が示されます。
これを踏まえて隠れ層の表現更新は
$h^{t + 1}_ x =σ_{t}(\sum _{y∈ \overline{N}(x)}^{n}M _{y→x}^{t})$と表されます。
$σ_{t}$は非線形変換です.
$y$から$x$に渡されるメッセージは、$y$の表現の線形変換です。またここで、重み$τ^{t}_{xy}$を導入します。形式的には、$M^{t} _{y→x} = \tau _{xy}^{t}W _{t}h^{t} _y
$となります。ここで、$W _t$は訓練を通じて学習された線形変換行列です。正式には、以下のような更新方程式になります。
$$
h^{t + 1}_ x =σ_{t}(\sum _{y∈ \overline{N}(x)}^{n} \tau _{xy}^{t}W _{t}h^{t} _y)
$$
ノード$x$の隣接ノードからの情報が$x$に渡される方法に直接影響するため、適切な再重み付けパラメーター$\tau ^{t} _{xy}$を取得することが重要です。一部の論文ではノードの次数を$\tau ^{t} _{xy}$として使用し、他の研究では繋がれたノードの特徴を使用して self attentionを$\tau ^{t} _{xy}$として計算しています。この論文では 、$\tau ^{t} _{xy}$を計算するために、リッチ曲率などのより高度な構造情報を使用されています。また、再重み付けパラメータ$\tau ^{t} _{xy}$は必ずしもスカラーではないことも知られています。スカラーと$F ^{t + 1}×F ^{t + 1}$行列の間であれば何でもかまいません。ベクトルはスカラーよりも表現力が高く、行列よりもトレーニングが容易であるため、実験ではベクトルとして$\tau ^{t} _{xy}$が選択されています。
離散リッチ曲率
先程も少し説明した通り、リーマン幾何学では、曲率は、滑らかなオブジェクトがフラットであること、または直線の場合はまっすぐであることからどの程度逸脱するかを測定します。同様の概念を、離散オブジェクトのスムーズでない設定にも拡張できます。
離散的で一般的なグラフで一般化しやすい曲率の定義は、断面曲率とリッチ曲率です。
曲率の計算
表面上の点$x$について、2つの接線ベクトル$v$と$w_x$を考えましょう。 $y$を$x$での接線ベクトル$v$の終点とします。 $v$に沿って$w_x$を$y$での接線ベクトル$w_y$に平行移動させます。表面が平坦な場合、$x$および$y$から$ε$離れた$w_x$および$w_y$に沿ったポイント$x'$と$y'$の距離は、$x$と$y$間の距離となります。
次に、$w_x$のすべての方向で平均化すると、接線ベクトル$v$のみに依存するリッチ曲率が得られます。
エッジ$(x,y)$上のリッチ曲率$κ_{xy}$は、Wasserstein距離W$(m_x,m_y)$を距離$d(x,y)$と比較することによって定義されます。式としては
$$
κ _{xy} = 1 − W(m _x,m _y)/ d (x,y)
$$
となります。
距離空間の点$x$におけるsmall ball$S_x$の自然な類似は、グラフのノード$x$の1ホップ近傍$N(x)$です。これにより、グラフの端のOllivier-Ricci曲率が動機付けられます。無向グラフ$G =(V、E)$が与えられたとき、ノード$x∈V$の隣接ノードの集合を$N(x)= {{x_1,x_2,・・・, x_k}}$とします。ここで、確率測度$m^α _x$を定義できます。

$α$は$[0,1]$内のパラメーターです。辺$(x,y)$の2つの端点$x,y$間の確率測度のワッサースタイン距離$W(m^α _x、m^α _y)$を計算するために、次の線形計画法によって最適輸送計画問題を解きます。
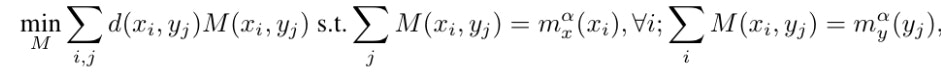
ここで、$M(x_i,y_j)$は、ノード$x_i$から$y_i$に、長さ$d(x_i,y_j)$の最短経路で送られる確率の量です。
グラフ理論では、Olivier-Ricci曲率が負の場合(つまり$W(m^α _x,m^α _y)> d(x,y)$の時)、辺$(x,y)$は$x$と$y$の近傍を接続するブリッジとして機能します。
ちょっと難しいですね。リッチ曲率とかちょっと調べてみたんですが、数学科とかがやっているような内容だったので(単なるイメージですが)、ここらへんはリッチ曲率というものをGNNに使いたいんだなぐらいの理解でいいのではないでしょうか。
CURVATURE-DRIVEN GRAPH CONVOLUTION
次に、グラフたたみ込みネットワークでリッチ曲率がどのように使用されるかを示します。直感的に、**曲率はメッセージがエッジをどれだけ容易に流れるかを測定し、畳み込みでメッセージパッシングをガイドするために使用できます。**しかし、その使用法は問題とデータに依存します。データドリブン戦略に頼り、リッチ曲率$κ_{xy}$をメッセージの重みとします。そして
$$
h^{t + 1}_ x =σ_{t}(\sum _{y∈ \overline{N}(x)}^{n} \tau _{xy}^{t}W _{t}h^{t} _y)
$$
の$\tau ^{t} _{xy}$にマッピングするマッピング関数を学習します。最初に、マッピングがエンドツーエンド(CurvGN-1)でどのように学習されるかを説明します。次に、マッピングを多値バージョンに拡張して、モデル(CurvGN-n)をより柔軟にします。
CurvGN-1
前述のように、$\tau ^{t} _{xy}$はスカラーと$F^{t + 1}×F^{t + 1}$行列の間の任意の値にすることができます。まず、$\tau ^{t} _{xy}$がスカラーであると仮定します。次に、マッピング関数は次のように定義できます。
$$
f^t:\kappa_{xy}→\tau ^{t} _{xy}
$$
エンドツーエンドの学習のためにGNNモデルに簡単に組み込むことができるため、多層パーセプトロン(MLP)を作成してマッピング関数$f^t$を近似します。
T番目の層の$MLP$を$MLP^t$と表します。集計時の数値の爆発を防ぐために、$x$のすべての近隣ノード$MLPt$($κ_{xy}$)にソフトマックス関数$S^t$を適用します。
$$
\tau ^{t} _{xy}=S^t(MLP^t(\kappa _{xy}))
$$
CurvGN-n
メッセージ$M ^t _{y→x}$は通常マルチチャネルです。曲率を使用して生成されたスカラーの重みは、異なるチャネルで必ずしも同じとは限りません。
$\tau ^{t} _{xy}$の表現力を向上させるために、先ほどの$f^t$と同様のマッピング関数を作成しますが、代わりに再重み付けベクトル$\tau ^{t} _{xy}∈R^{F^{t + 1}}$を生成します。つまり、それぞれのメッセージチャネルごとにの重み付けする方法を学びます。原則として、メッセージを再重み付けするために次元$R^{F^{t + 1}}×R^{F^{t + 1}}$の行列を学習することもできます。ただし、ベクトルにはトレーニングするパラメーターが少ないという利点があり、実際にはベクトルで十分であることがわかります。
CurvGN-1と同じ戦略で、ベクトル$\tau ^{t} _{xy}$は、$F^{t + 1}$出力を持つ$MLP^t$を適用することによって計算されます。次に、各メッセージチャネルでMLP出力を個別に正規化するチャネルごとのソフトマックス関数$S^t$を適用します。$
\tau ^{t} _{xy}=S^t(MLP^t(\kappa _{xy}))
$をさきほどの式に代入すると、以下の式が得られます。
$$
h^{t + 1}_ x =σ_{t}(\sum _{y∈ \overline{N}(x)}^{n} diag(\tau _{xy}^{t})W _{t}h^{t} _y)
$$
ここで、$diag(\tau _{xy}^{t})$は、対角要素が$\tau ^{t} _{xy}$の要素である対角行列です。
EXPERIMENTS
合成グラフと実際のグラフの両方で評価されています。この方法は、特に、**トポロジー構造が不均一になる傾向がある大きくて密度の高いグラフで、最新の方法よりも優れています。**予測能力を実証するために、合成実験でさまざまなグラフ理論モデルとさまざまなパラメーター設定を使用して、曲率の情報がグラフの畳み込みにどのように役立つかについての洞察を得ます。
GRAPH THEORETICAL MODELS
異なるグラフ理論モデルを使用して合成データを生成します。まず、グラフをコミュニティに分割することを想定した確率ブロックモデル(SBM)(Holland et al。、1983)から始めます。それぞれ1000ノードのランダムグラフを作成し、ノード集合を5つの互いに素なコミュニティ(かぶりがない)に均等に分割します。同じコミュニティのノードは同じクラスラベルを持っています。エッジは、同じコミュニティ内のノードの場合はコミュニティ内確率pで、異なるコミュニティのノードの場合はコミュニティ間確率qでランダムにサンプリングされます。ランダムに100個のグラフを作成します。pの範囲は{0.05、0.07、・・、0.23}で、qの範囲は{0.0、0.005、・・、0.045}です。生成されたグラフごとに、ランダムに400ノードをトレーニングセットとして選択し、別の400ノードを検証セットとして、残りの200ノードをテストセットとして選択します。ランダムに生成された次元10の特徴を各ノードに割り当て、それらをCurvGNの有益でない入力として使用します。
すべての手法を100個のランダムグラフで実行しました。各グラフについて、トレーニングと推論タスクを10回実行し、平均精度を取得しました。トレーニングごとに、200エポックを実行し、検証セットを使用して早期停止します。図3は、すべての手法のヒートマップを示しています。各ヒートマップのタイトルには、すべてのパラメーター設定の最大および平均パフォーマンスが含まれています。図3(c)では、異なるサイズのグラフで同じ実験を実行し、平均精度を載せてあります。

ヒートマップから、VanillaGN、GCN、およびGATはランダムな推測よりも優れていないことがわかります。これは、ノード次数情報は不十分であることを意味します。一方、CurvGN-1によるパフォーマンスの向上が確認できます。さらに、CurvGN-nはCurvGN-1よりも優れており、曲率に基づくマルチチャネルの再重み付けが有益であることを示唆しています。さらに、図3(c)では、グラフのサイズが大きくなると曲率の利点が大きくなることがわかります。グラフの畳み込みは、小さなグラフ設定ではグラフ構造を完全に探索するのに十分であり、高度な構造情報はサイズが大きく、構造多様性が豊富なグラフで重要になると仮定します。
また、図4に(p、q)=(0.21、0.025)で生成された特定のグラフで予測結果を視覚化します。

CurvGN-1とCurvGN-nは、いくつかのコミュニティのデータのごく一部を除いて、高精度に予測できています。一方、他のベースラインは異なるコミュニティを混合する可能性があるのが分かります。
リッチ曲率の表現力をさらに調べるために、いくつかよく知られているグラフ理論モデルを使用して実験します。
・navigable small world graphs(Kleinberg)
・Watts-Strogatz network
・Newman-Watts network
(各ネットワークの説明は略。)
これらすべてネットワークので、リングをさまざまなコミュニティに分割し、確率ブロックモデルと同様の実験をします。
これらのさまざまなグラフモデルで5つの方法すべてを比較し、さまざまなパラメーター設定での平均精度を表1に示します。

さまざまなパラメーター設定で平均化しているため、これらの結果の標準偏差は一般に大きくなっています。 CurvGN-nのパフォーマンスは、他の方法よりも常に優れています。これは、曲率情報が幅広いグラフで有益であることを裏付けています。また、GCNとGATが実際にWatts-StrogatzモデルとNewman-Wattsモデルでうまく機能していることにも注意してください。これは、これらのネットワークでは、エッジの再配線と追加によってノードの次数の違いが大きくなるためです。異なるコミュニティを横断する橋は、ノードの次数が高くなる傾向があります。したがって、ノード次数は有用な構造情報を持ち、グラフの畳み込みに役立ちます。 SBMとKleinbergのモデルでは、これらのモデルと同じノード次数情報の利点は確認されていません。ノード次数は橋の位置と相関していません。
現実世界のグラフでは?
実際に存在するネットワークのデータセットを用いて
CurvGN-1とCurvGN-nをいくつかの強力な以下のベースラインと比較します。
・GCN
・GAT
・多層パーセプトロン(MLP)
・MoNet(Monti et al。、2017)
・WSCN(Morris et al。、2019)
・平均集計(GS-mean)を使用したGraphSAGE(Hamilton et al。、2017)。
提案手法は、比較的小さなグラフでの最新手法と同等であり、異種のグラフトポロジを持つ傾向がある大規模で高密度のグラフでの最新の方法を大幅に上回っています。
データセット
3つの引用ネットワークデータセットを使用します:Cora、citetseer、PubMed(Sen et al。、2008)。 Coraとcitetseerはどちらも比較的小さく疎です。数千のノードとエッジを持ち、ノードの平均次数は2未満です。また、4つの追加データセットを使用します。CoauthorCSとCoauthor Physicsは、KDDカップ2016チャレンジのMicrosoftアカデミックグラフに基づく共著者グラフ2つと、 McAuley et al(2015)で使用されたAmazon共同購入グラフのセグメントであるAmazon ComputersとAmazon Photosのの2つ。これらのグラフは、PubMedとともに、大きくて密度の高いグラフです。これらのグラフには、平均ノード次数が20である1万を超えるノードと20万のエッジがあります。Kipf&Welling(2016)で使用されている半教師あり学習設定と同様に、正確なデータ分割を使用します。 クラスあたり20ノードをトレーニングに、500ノードを検証に、1000ノードをテストに使用します。トレーニング段階では、すべてのデータセットに対してL2正則化をλ= 0.0005に設定しました。また、すべてのモデルはGlorot初期化によって初期化され、学習率0.005のAdam SGDオプティマイザーを使用してクロスエントロピー損失を最小化することによってトレーニングされます。
100エポックでのテストノードの分類精度の平均と標準偏差を、表2に示します。

提案手法は、比較的小さいグラフの最先端の方法と同等であり、大きくて密度の高いグラフで優れたパフォーマンスを実現します。これは、先ほどからの結論と一致しています。グラフが大きく、トポロジが不均一である場合、高度な構造情報がグラフの畳み込みで重要になります。
結論
高度なグラフ構造情報、つまりグラフの曲率を活用する新しいグラフ畳み込みネットワークを紹介しました。曲率情報は、合成データと実際のデータセット、特に大きくて密度の高いグラフで優れたパフォーマンスを達成するのに効果的です。