はじめに
グラフでの機械学習は、ドラッグデザインからソーシャルネットワークでの友情の推薦まで、さまざまな分野に利用されてます。この分野の主な課題は、どのようにグラフ構造を表現またはエンコードして、機械学習モデルで簡単に活用できるようにする方法を見つけることです。従来、機械学習のアプローチは、ユーザー定義のヒューリスティックに依存して、グラフに関する構造情報(次数統計やカーネル関数など)をエンコードする機能を抽出していました。ただし、近年、深層学習と非線形次元削減に基づく手法を使用して、グラフ構造を低次元の埋め込みに自動的にエンコードする手法が急増しています。この記事や続きの記事で、それらの手法を紹介していきたいと思います。てか、まじでだれか参考書日本語で出してください。今のところ英弱にはきつい分野だ。。。
ちなみに、こちらの論文を日本語でざっと解説しようという趣旨です今回の記事は。
イントロダクション
グラフは現代の機械学習で重要な位置を占めています。グラフ構造化データを使用して、予測を行ったり、新しいパターンを発見したりする機械学習アプリケーションがたくさんあります。たとえば、生物学的相互作用グラフでのタンパク質の役割の分類、コラボレーションネットワークでの人物の役割の予測、ソーシャルネットワークでのユーザーへの新しい友達の推奨、既存の薬物分子の新しい治療への応用の予測などが考えられます。さて、ここで質問です。一体、どのようにしてグラフを機械学習モデルに組み込むのでしょうか?
これが実はこの分野のメイン課題です。機械学習の観点から言うと、グラフ構造に関するこの高次元の非ユークリッド情報を特徴ベクトルにエンコードする簡単な方法がありません。従来のアプローチは、特徴量を手動設計するようなものでした。これには課題がありました。手動設計だと時間と費用が掛かりすぎること可能性があるのです。
しかし、最近グラフに関する構造情報をエンコードする「表現」を学習しようとするアプローチが急増しています。(つまり、特徴量を手動で設計しなくてもよい手法)
グラフの表現学習の概観(最近のアプローチのほう)
表現学習手法の考え方を説明します。表現学習では、ノードまたは(部分)グラフ全体を、低次元のベクトル空間$R_d$の点として埋め込むマッピングを学習します。目標は、このマッピングを最適化して、埋め込み(つまりベクトル)が元のグラフ構造を反映するようにすることです。そして、埋め込み空間を最適化した後、学習した埋め込みを、下流の機械学習タスクの特徴入力として使用できます。
従来のアプローチと最近のアプローチの主な違い
主な違いはグラフ構造の表現の問題をどのように扱うかです。
以前の手法では、この問題を前処理ステップとして扱い、手動で作成した統計を使用して構造情報を抽出していました。
表現学習アプローチ(最近のアプローチ)はこの問題を機械学習タスク自体として扱い、データドリブンなアプローチを使用してグラフ構造をエンコードする埋め込みを学習します。
表現学習アプローチ
ここからは、主要な表現学習アプローチを紹介してこうと思います。
ちなみに、今回はノードエンベディング、そのなかの一部のアプローチのみに絞って紹介します。
ノードエンベディング
ノードをグラフの位置とローカルグラフ近傍の構造を要約する低次元ベクトルとしてエンコードすることです。
これらの低次元の埋め込みは、潜在空間へのノードのエンコードまたは投影と見なすことができます。この潜在空間の幾何関係は、元のグラフの相互作用(エッジなど)に対応します。
図で見てみましょう。
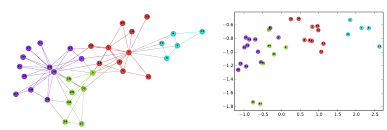
ちょっと解像度わるくて申し訳ないんですが、これがノードエンベディングです。今回の例ではノードを2次元ベクトル空間に埋め込んでますね。つまり、ノードの分散表現を得ているわけです。また、右の図をみるとある程度ネットワークに含まれるコミュニティ構造がキャプチャできてるようですね。右の図でも各色である程度まとまっていることからそれがいえます。
さて、視覚的に理解しました。次は詳細にどのような手法(つまり埋め込み方)があるのか以下の4つの観点で紹介していきます。
1.グラフ$G=(V,E)$で定義されたノードのペア毎の類似度を測る関数$s_g:V×V→R^+$。
2.ノードの埋め込みを生成するエンコーダー関数$ENC$。この関数には、学習段階に最適化されるトレーニング可能なパラメータがいくつか含まれています。
3.生成された埋め込みからペア毎の類似値を再構築するデコーダー関数$DEC$。この関数には通常、トレーニング可能なパラメーターは含まれていません。
4.モデルをトレーニングするために再構成のクオリティーがどのように評価されるか。つまり$DEC(z_i、z_j)$がユーザーが採用した類似度$s_g(v_i、v_j)$とどのように比較されるかを決定する損失関数 。
さまざまなノード埋め込みアプローチの主な方法的な違いは、これらの4つの構成要素をどのように定義するかです。
ノードエンベディングアルゴリズムの大半は「Shallow embedding」に依存する。
これらのShallow embeddingアプローチの場合、エンコーダー関数(ノードをベクトル空間に写す関数)は、次のように表せます。
$$
ENC(v_i) = Zv_i
$$
ここで、$Z∈R^{d×|V|}$は、すべてのノードの埋め込みベクトルを並べた行列です。また、$v_i∈I_V$は、ノード$v_i$に対応する$Z$の列を示すワンホットインジケーターベクトルです。(※[0,0,0,1]みたいなベクトル)
そして、この Shallow embedding アプローチ では埋め込み行列$Z$が直接最適化されます。
今後の説明にちょくちょく出てくるので頭に入れておいてください。
さて、話を戻すと ノードエンベディングの手法は以下の二つに分けられます。
・Factorization-based approaches
ノードの分散表現を学習するための初期の方法。今回は詳しく説明しません。
・ Random walk approaches
最近のはやり。ランダムウォーク統計に基づいてノードの埋め込みを学習します。
彼らの重要な革新は、ノードがグラフ上で短いランダムウォークで共起する傾向がある時にノード埋め込みが同様の傾向を持つように、ノードの埋め込みを最適化することです。
ここで、ランダムウォークを簡単に説明します。以下の図をご覧ください。

ランダムウォークベースの手法は、各ノードv_iから始まる多数の固定長なランダムに動いた時の軌跡をサンプリングします。次に、2つの埋め込み$z_i$と$z_j$の間の内積または角度が$v_i$から始まる固定長のランダムウォークで$v_j$を訪問する確率に(ほぼ)比例するように、埋め込みベクトルが最適化されます。
ノードの類似性の確定的測定を使用する代わりに、これらのランダムウォーク法は、ノードの類似性の柔軟で確率的な測定を採用し、多くの設定で優れたパフォーマンスを発揮しました。
さて、具体的にランダムウォークベースの手法を見ていきましょう。
1.DeepWalk and node2vec
これらのアプローチでは、確定的なノードの類似度をデコードする代わりに、埋め込みを最適化してランダムウォークの統計をエンコードします。これらのアプローチの背後にある基本的な考え方は、(大まかに)以下のように埋め込みを学習することです。
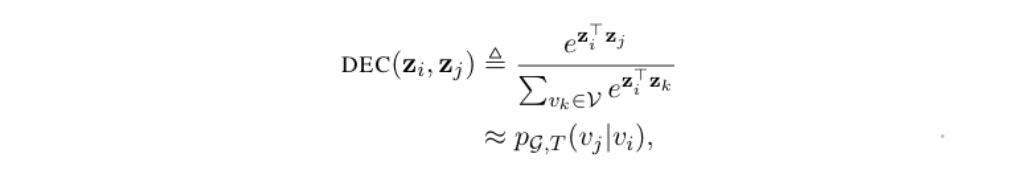
ここで、$p_{g,T}(v_j | v_i)$は、$v_i$から始まる長さ$T$のランダムウォークで{v_j}を訪問する確率です。$T$は通常、$T∈{2、...、10}$の範囲で定義されます。$p_{g,T}(v_j | v_i)$は確率的かつ非対称です。より正式には、これらのアプローチは、次の交差エントロピー損失を最小化しようとします。

ここで、トレーニングセット$D$は、各ノードから開始するランダムウォークをサンプリングすることによって生成されます(つまり、各ノード$v_i$のN個のペアは、分布$(v_i、v_j)〜p_{g,T}(v_j | v_j)$からサンプリングされます)。また、計算時間の問題でDeepWalkとnode2vecは異なる最適化と近似を使用して、$L$の損失を計算します。
DeepWalkは、計算を高速化するために2分木構造を使用して正規化係数を計算する「階層的ソフトマックス」を採用しています。対照的に, node2vecは「負のサンプリング」を用いて$L$を近似しています.(これだけじゃ意味不明ですよね。ここはまた別の記事にしようと思います。)
これらのほかに、 node2vecではランダムウォークの柔軟な定義が可能であるのに対し、DeepWalkではグラフ上の単純で偏りのないランダムウォークが使用されます。特に、node2vecでは、ランダムウォークにバイアスをかける2つのランダムウォークハイパーパラメータ$p$と$q$を導入しています。$p$はノードを再訪する確率を制御し,$q$はノードの1ホップ近傍を再訪する確率を制御します.これらのハイパーパラメータを導入することで, node2vec は,幅優先探索や深さ優先探索に近い探索の間をスムーズに補間することができます.
$p$と$q$を調整することで,コミュニティ構造を重視するのか、それとも,局所的な構造的役割を重視するのかを調整することができます。探索の方針を変えられるんですね。それがこの図で説明されています。
2.Large-scale information network embeddings (LINE)
ここでランダムウォークには基づきませんが、DeepWalkやnode2vecと同時期に出たもう1つのShallow embeddingアプローチが、LINEです。LINEには、目的関数が二つあり、それぞれを組み合わせます。1次のノード類似度を最適化する目的関数は、シグモイド関数に基づくデコーダを使用します。
$$
DEC(z_i,z_j) = \frac{1}{1 + e^{−\bf{z_i}\bf{z_j}}}
$$
2 次のエンコーダ/デコーダの目的関数は似ていますが、2 ホップの隣接領域を考慮しており、以下の式のエンコーダを使用します。
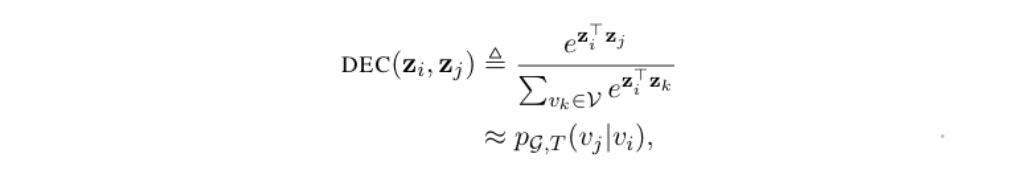
1 次および 2 次の目的関数は、KLdivergence メトリック から導出された損失関数を使用して最適化されます。(Kullback-Leibler divergence ( KLダイバージェンス、KL情報量 )は、2つの確率分布がどの程度似ているかを表す尺度。)
LINEは、確率的デコーダと損失を使用するという点でnode2vecとDeepWalkに関連していますが、固定長ランダムウォークで組み合わせるのではなく、1次と2次の類似度を明示的に因数分解します。
3.HARP: Extending random-walk embeddings via graph pre-processing.
グラフの前処理ステップによってさまざまなランダムウォークアプローチを改善します。
このアプローチでは、グラフを粗くする手順を使って、Gの関連ノードをまとめて「スーパーノード」に折りたたみ、DeepWalk、node2vec、またはLINEをこの粗くしたグラフに対して実行します。粗いバージョンのGをベクトル空間に埋め込んだ後、各スーパーノードの学習された埋め込みが、スーパーノードの構成ノードのランダムウォーク埋め込みの初期値として使用されます(グラフの「より細かい」バージョンの最適化の別のラウンドで)。この一般的なプロセスは、さまざまなレベルの粗さで階層的に繰り返すことができ、DeepWalk、node2vec、およびLINEのパフォーマンスを一貫して向上させることが示されています。
紹介されていた主要なアプローチは以上です。
shallow embedding approache の欠点
これまでに紹介したすべてのnode embedding 手法はshallow embedding手法であり、エンコーダは単なる埋め込みルックアップです。ただし、これらのshallow embeddingアプローチは、ノードごとに一意の埋め込みベクトルを個別にトレーニングするため、いくつかの欠点があります。
1.エンコーダー内のノード間でパラメーターが共有されることはありませんパラメータの共有は正則化の強力な形式として機能する可能性があるため、これは統計的に非効率になる可能性があります。また、shallow embeddingメソッドのパラメータの数は必然的に$O(| V |)$として増加するため、計算上も非効率的です。
2.shallow embeddingでは、エンコード中にノード属性を活用できません。多くのグラフでは、ノードに属性情報(ソーシャルネットワークのユーザープロファイルなど)がついており、グラフ内のノードの位置と役割に関して非常に有益なことがよくあります。もったいないですよね。
3.shallow embeddingは本質的にトランスダクティブ[29]です。つまり、学習する段階で存在したノードに対してのみ埋め込みを生成することができ,追加の最適化ラウンドが実行されない限り,以前には与えられなかったノードに対しての埋め込みを生成することはできません。これは,進化するグラフ,メモリに完全に格納できない大規模なグラフ,学習後に新しいグラフに一般化する必要がある領域では,適しません。
最近では、これらの欠点の一部またはすべてに対処するための多くのアプローチが提案されています。これらのアプローチは、shallow embedding方法とは異なり、より複雑なエンコーダを使用します。また、これらは多くの場合、ディープニューラルネットワークに基づいており、より一般的にはグラフの構造と属性に依存しています。
ということで次回はそのより進化したアプローチについて触れていこうと思います。
まとめ
かいてて思ったんですが、やっぱり本論文読まないと何のことかさっぱりな部分がありますね。勉強して知識のアップデートがあれば更新しようと思います。とりあえず簡単にまとめると
*node embedding というのはノード間の関係を低次元空間に写像するもの
*低次元空間に写像できれば、機械学習モデルの入力として使える
*グラフの表現学習=embeddingの学習(つまりどういう写像がいいのかを学習)
*Shallow embeddingはnode embeddingの一部。
*Shallow embeddingには欠点がある。
てとこでしょうか。で、元論文では、この流れで新しい手法を紹介していくという構成になっていました。次の記事では続きを書いていきます。