こんにちは!毎回おなじみの論文を紹介したいと思います。今回も訳をメインにところどころ補助を入れていきます。初学者の助けに少しでも慣れれば幸いです。
分からない場所があれば本論文をのぞいてみてください。
論文はこちら
HyperGCN: A New Method of Training Graph Convolutional Networks on Hypergraphs
Abst
共著、共引用、電子メール通信などの多くの現実のネットワークは、複雑な構造をしています。ハイパーグラフは、そのような複雑な関係をモデル化するための柔軟で自然なモデリングツールを提供します。現実世界のネットワークにおけるそのような複雑な関係は、当然、ハイパーグラフによる学習の問題のモチベーションです。人気のある学習パラダイムのタスクは、ハイパーグラフベースの半教師あり学習(SSL)で、ハイパーグラフのラベル付けされていない頂点にラベルを割り当てることを対象としています。グラフ畳み込みネットワーク(GCN)がグラフベースのSSLに効果的であるという事実をモチベーション以に、ハイパーグラフでSSLのGCNをトレーニングする新しい方法であるHyperGCNを提案します。
Introduction
共著、共引用、電子メール通信などの多くの現実のネットワークデータセットでは、関係は複雑であり、ノードのペア毎の関係という問題では収まりません。ハイパーグラフは、そのような複雑な関係をモデル化するための柔軟で自然なモデリングツールを提供します。たとえば、共著ネットワークでは、著者(ハイパーエッジ)が3つ以上のドキュメント(頂点)の共著者になることができます。
人気のある学習パラダイムは、グラフベース/ハイパーグラフベースの半教師あり学習(SSL)です。グラフ/ハイパーグラフのラベル付けされていない頂点にラベルを割り当てることがそのタスクです。 多くの手法は、目的変数(objective)で、明示的なラプラス正則化を使用していますが、最先端の手法は、ニューラルネットワークを介して暗黙的にグラフ/ハイパーグラフ構造G =(V、E)をf(G、X)にエンコードします。(X【入力】には、ドキュメントのテキスト属性など、頂点の初期特徴量が含まれます)。
明示的なラプラス正則化は、各エッジ/ハイパーエッジの頂点間の類似性を前提としていますが、グラフたたみ込みネットワーク(GCN)の暗黙的な正則化は、この制限を回避し、組み合わせ最適化における幅広い問題への適用を可能にします。
この研究では、HyperGCNを提案します。これは、ハイパーグラフ上のGCNの新しいトレーニングスキームです。ハイパーエッジは類似性をエンコードしますが、ハイパーエッジが類似性をエンコードしない組み合わせ最適化でも使用されます。ハイパーグラフの組み合わせ最適化は、現実のネットワーク分析にとって非常に重要だといわれ始めています。
HyperGCNは、ハイパーグラフの各ハイパーエッジを、ハイパーエッジの頂点を接続するノードごとのエッジのセットで近似し、学習問題を近似上のグラフ学習問題として扱います。
最先端の手法、ハイパーグラフニューラルネットワーク(HGNN)は各ハイパーエッジを
クリーク(頂点の部分集合 C に属するあらゆる2つの頂点を繋ぐ辺が存在する場合)
で近似するため、各ハイパーエッジに二次関数的な数のエッジが必要ですが、この方法、つまりHyperGCNでは線形数のエッジでOKです。

表1に示すように、本手法の高速なバリアントは、実際のハイパーグラフ(DBLPとPubmed)で最も密度の高いk部分ハイパーグラフとSSLの合成データのトレーニング時間を短縮します(密度も高い)。まとめるといかの貢献をしました。
• HyperGCNを提案します。これは、ハイパーグラフのスペクトル理論からの既存のツールを使用して、ハイパーグラフ上でグラフ畳み込みネットワーク(GCN)をトレーニングする新しい方法です
• 属性付きハイパーグラフと組み合わせ最適化でのSSLの問題にHyperGCNを適用します。詳細な実験により、最先端のHGNN、およびほかのベースラインと比較してその有効性を実証しています。
• HGNNよりもHyperGCNを使用するべき時を議論しました。
HyperGCNのモチベーションはハイパーエッジの頂点の類似性に基づいていますが、ハイパーエッジが類似性をエンコードしない組み合わせ最適化に効果的に使用できることを示しています。
Graph convolutional network
$N = | V |$の$G =(V、E)$を、隣接$A∈R^{N×N}$とデータ行列X∈R^{N×p}を持つ単純な無向グラフとします。また各ノード$v∈V$ごとにp次元の実数値ベクトル表現が特徴量としてあるとします。
グラフのたたみ込みの基本的な定式化Kipf and Welling [2017]はたたみ込みの定理Mallat [1999]に由来しています。この定式化より、実数値のグラフ信号$S∈R^N$とフィルター信号$F∈RN$のたたみ込みCは、$C ≈ (w_0 + w_1L˜)S$と近似できることが示されました。ここで、
・$w_0$と$w_1$は学習された重み
・$L~= 2L/λ_N− I$はスケーリングされたグラフラプラシアン、
・λ_Nは対称的に正規化されたグラフラプラシアン$L = I − D ^{− 1 /2}AD^{− 1 /2}$の最大固有値
・$D = diag(d_1,・・・,d_N)$は、要素$\sum_{j=1,j\neq i}^{N} A_{ji}$をもつ対角次数行列
です。フィルターFはグラフ(グラフラプラシアンL)の構造に依存します。畳み込み定理からの詳細な導出は、グラフ信号処理からの既存の研究を参照されたし。
ここで重要な点は、2つのグラフ信号のたたみ込みがグラフラプラシアンLの線形関数であることです。
ここでこの論文で使われた記号をそれぞれ説明した表をお見せします。

GCN Kipf and Welling [2017]
単純な2層のGCNのフォワードモデルは、次の単純な形式を取ります。

ここで、$Θ^{(1)}∈R^ {p×h}$は$h$個の隠れ層ユニットを持つ[入力層-隠れ層]の重み行列、$Θ^{(2)}∈R^ {h×r}$は[隠れ層-出力層]の重み行列です。
GCN training for SSL
マルチクラスのqクラスの分類ということで、ラベル付きのノードの集合$V_L$でクロスエントロピーを最小化します。
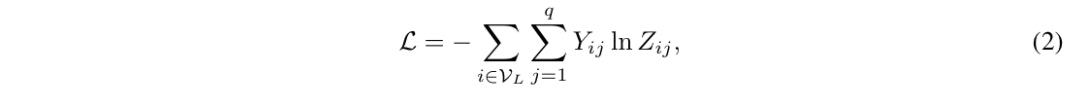
重み$Θ^{(1)}$および$Θ^{(2)}$は、最急降下法を使用して学習させます.
HyperGCN: Hypergraph Convolutional Network
ここで、やっと登場...
無向ハイパーグラフ$H =(V、E)$の半教師ありハイパーノード分類を検討します。 $| V |= n $, $ | E | = m$,およびラベル付きハイパーノードの小さな集合を$V_L$とします。各ハイパーノード$v∈V = {1,・・・,n}$は、$X∈R ^{n×p}$で与えられる次元pの特徴ベクトル$x_v∈R ^p$にも関連付けられています。タスクは、ラベルがついていないすべてのハイパーノードのラベルを予測することです。
概要:ここで重要なことは, 同じハイパーエッジのハイパーノードは似ているため、同じラベルを共有する可能性が高いということです。$ {h_v:v∈V}$を使用して$V$内のハイパーノードの表現を表すとします。任意の$e ∈ E(エッジ)$に対して、関数$max_{i,j∈e}|| h_i − h_j ||^ 2$は、 Eのハイパーノードに対応するベクトルが互いに「近い」場合にのみ「小さい」ということになります。したがって、正則化子としての$\sum_{e ∈ E}max_{i,j∈e}|| h_i − h_j ||^ 2$は、同様の表現を持つ同じハイパーエッジ内で、ハイパーノードの目的(objective)を達成する可能性が高いです。ただし、明示的な正則化子として使用する代わりに、ハイパーグラフの適切に定義されたラプラシアンに対してGCNを使用することで、同じ目標を達成できます。言い換えると、ハイパーグラフラプラシアンの概念を、この目的を達成する暗黙の正則化子として使用します。
図1は、論文中で示された1-HyperGCNというメソッドの1epochを表した図です。

Hypergraph Laplacian
GCNの重要な要素は、与えられたグラフGのグラフラプラシアンです。したがって、ハイパーグラフ用のGCNベースのSSLメソッドを考えるには、まずハイパーグラフ用のラプラシアンを定義する必要があります。そのような方法の1つは、非線形関数$L:R ^n→R ^n$です(グラフのラプラシアン行列は、線形関数$L:R ^n→R ^n$と見なすことができます)。
Definition 1 (Hypergraph Laplacian Chan et al. [2018], Louis [2015]1)
ハイパーノードで定義された実数値の信号$S∈R^n$が与えられると、$L(S)$は次のように計算されます。
1.各ハイパーエッジ$e∈E$について、$(i_e ,j_e):= argmax_{i,j∈e}| S_i − S_j |$、となるように関係をランダムに分割
2.頂点セット$V$の重み付きグラフ$G_S$は、エッジ${{i_e、j_e}:e∈E}$に重みw$({i_e、j_e}):= w(e)$を$G_S$に追加することによって構築されます。ここで、w(e)はハイパーエッジeの重みです。次に、各頂点$v$に、$G_S$の頂点の次数が$d_v$と等しくなるように自己ループが追加されます。 $A_S$がグラフ$G_S$の加重隣接行列を表すとします。
3.対称的に正規化されたハイパーグラフラプラシアンは$L(S):=(I − D^{− 1/2} A_SD^−{1/2})S$となります。
1-HyperGCN
概説したラプラシアン構築手順に従うことにより、正規化された隣接行列 A⁻ _Sを持つ単純なグラフ$G_S$を得ることができます。次に、この単純なグラフ$G_S$に対してGCNを実行します。式(1)のグラフたたみ込み演算は、$G_S$のハイパーノード$v∈V$に適用されると、ニューラルメッセージパッシングフレームワークで実行されます。定式化すると、
$$
h_{v} ^{(\tau+1)}=\sigma((\Theta^{(\tau)})^T\sum_{u\in N(v)}([\bar{A}_S^{(\tau)}]_{v,u}・h_u^{(\tau)})
$$
となります。ここで、
$\tau$:エポック数
$h_{v} ^{(\tau+1)}$:ノード$v$の新しい隠れ層の表現
$\sigma$:非線形活性化関数
$\Theta$:学習された重みの行列
$N(v)$:$v$の近接集合
$[\bar{A}_S^{(\tau)}]_{v,u}$:正規化後のエッジ${v,u}$の重み
$h_{u}^{(\tau)}$:$u$の近隣の前の隠れ層の表現
です。ハイパーノードの埋め込みとともに、隣接行列も各エポックで再推定されることに注意してください。
図1は、5つのハイパーエッジが発生したハイパーノード$v$を示しています。 $(i_e,j_e)$によって与えられる各ハイパーエッジに対して、厳密に1つの代表的な単純エッジを考慮します。ここで、エポックτに対して、$(i_e,j_e)=argmax_{i,j\in e}||(\Theta^{(\tau)})^T(h_{i}^{(\tau)}-h_{j}^{(\tau)})||$となります。
ハイパーノード$v$は、すべての代表的な単純なエッジの一部ではない場合があります(図では3つだけを示しています)。次に、$v$で従来のグラフ畳み込み演算を使用し、それに発生する単純なエッジのみを考慮します。収束するまで、訓練の各エポックτで各ハイパーノード$v∈V$にこの操作を適用することに注意してください。
Connection to total variation on hypergraphs:
1-HyperGCNモデルは、ハイパーグラフの総変動に基づいて暗黙的な正則化を実行していると見なすことができます。以前の研究では、明示的な正則化とハイパーグラフ構造のみがSSL設定のハイパーノード分類に使用されていました。一方、HyperGCNは、ハイパーグラフ構造を使用することも、ハイパーノードで使用可能な特徴量(ドキュメントのテキスト属性など)を利用することもできます。
HyperGCN:メディエーターによる1-HyperGCNの強化
ハイパーグラフラプラシアンのある特異な側面は、各ハイパーエッジeが単一のノードごとの単純な辺として表されることです。このハイパーグラフラプラシアンは、指定エポックの$K_e := {{k ∈ e : k \neq i_e, k \neq j_e}} $のハイパーノードを無視します。最近、$K_e$のハイパーノードが「メディエーター:仲介者」として機能する一般化されたハイパーグラフラプラシアンが、上記のラプラシアンに必要なすべての特性を満たすことが示されています。
図2で2つのラプラシアンを図で比較しています。ハイパーエッジのサイズが2の場合、$i_e$と$j_e$をエッジで接続することに注意してください。
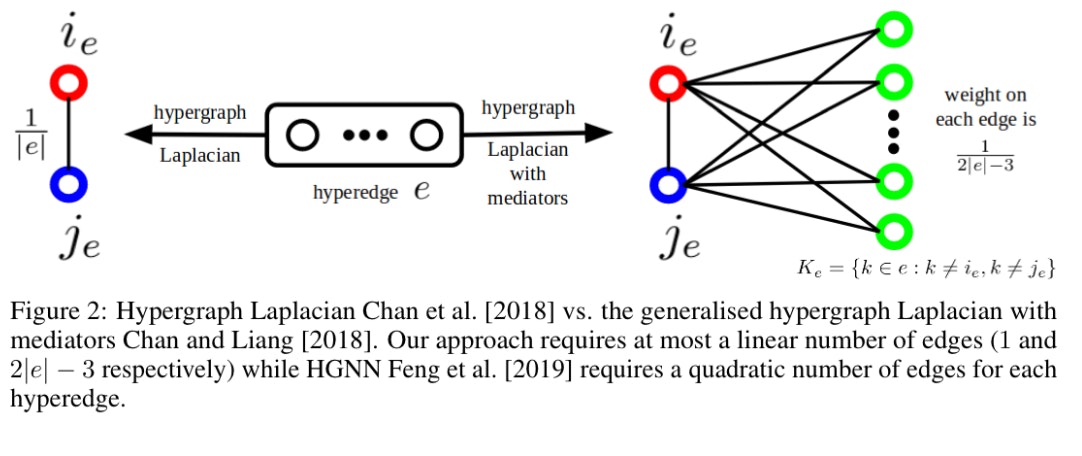
また、メディエーターのハイパーグラフラプラシアンに関連付けられた単純なグラフでGCNを実行します(図2の右側)
ハイパーグラフラプラシアン(メディエーターを含む)の各ハイパーエッジのエッジの重みの合計は、1 となります。
FastHyperGCN
最初の特徴量X(重みなし)だけを使用して、ハイパーグラフラプラシアン行列(メディエーター付き)を作成するメソッドをFastHyperGCNと呼びます。行列はトレーニングの前に1回だけ計算されるため(各エポックでは計算されない)、FastHyperGCNのトレーニング時間は他の方法のトレーニング時間よりもはるかに短くなります。
Experiments for semi-supervised learning
実在しているハイパーグラフで実験を行いました。
提案したHyperGCN、1-HyperGCN、FastHyperGCNを以下のベースラインと比較しました。
各データセットでのタスクは、ドキュメントが属するトピックを予測することです(マルチクラス分類)。統計を表3にまとめます。
データセットの詳細については、補足を参照してください。 200エポックのすべてのメソッドをトレーニングし、以前の研究、Kipf and Welling [2017]と同じハイパーパラメーターを使用しました。 100の異なるtrainとtestの分割の平均テスト誤差と標準偏差を報告します。
Analysis of results
【すみません。ここの分析部分は数式が多く書ききれなくなったのでご自分でご確認お願いします。】
上記の分析から、提案された手法(HyperGCNおよびFastHyperGCN)は、大きなノイズのあるハイパーエッジを持つハイパーグラフにおいては、HGNNよりも優れていると結論付けます。これは、次に説明する組み合わせ最適化の実験(表6)にも当てはまります。
HyperGCN for combinatorial optimisation
私達は最も密度の高いk-部分サブハイパーグラフ問題の学習ベースのアプローチとして、HyperGCNを使用しました。ハイパーグラフのNP-hardな問題は、現実のネットワーク分析にとって非常に重要であることが最近強調されています。私たちの問題は、ハイパーグラフ(V、E)が与えられた場合、Vに含まれるハイパーエッジの数を最大化するために、k個のハイパーノードのサブセットW⊆Vを見つけることです。
問題の貪欲な発見的方法は、最大次数のk個のハイパーノードを選択することです。これを「MaxDegree」と呼びます。もう1つの貪欲な方法は、最小次数のハイパーノードで構成される現在の(残差)ハイパーグラフからすべてのハイパーエッジを繰り返し削除することです。この手順をn − k回繰り返し、残りのk個のハイパーノードの密度を考慮します。これを「RemoveMinDegree」と呼びます。
実験:結果を表6に示します。合成で生成されたデータセットを使用して、すべての学習ベースのモデルをトレーニングしました。アプローチと合成データの詳細は補足にあります。表6に示されているように、提案されたHyperGCNは、次数が大きい少数の頂点と次数が小さい多数の頂点を含むpubmedデータセットを除いて、他のすべてのアプローチよりも優れています。

定性的な分析:図3は、Cora共著ハイパーグラフ上でのRemoveMinDegreeおよびHyperGCNによる視覚化を示しています。一般に、近くの頂点のクラスターには、それらを接続する複数のハイパーエッジがあります。緑の頂点のみのクラスターは、メソッドがクラスターによって誘発されたハイパーエッジ内のすべての頂点を含む可能性が高いことを示しています。 HyperGCNの図には、RemoveMinDegreeの図よりも密度の高い緑色のクラスターがあります。

Conclusion
ハイパーグラフのスペクトル理論からのツールを使用してハイパーグラフでGCNをトレーニングする新しい方法であるHyperGCNを提案しました。 SSLと組み合わせ最適化におけるHyperGCNの有効性を示しました。
一応本文はここまででした。ところどころ訳に困るところがあり、まだまだだなと感じています。特にobjectiveをどう訳そうか迷いました。いい訳があれば教えてください。。。では、今回はこの辺で。

