非可換代数計算機を作った with MATLAB
数学には様々な非可換環(代数)がありますが、そのクラスをMATLABのsymbolic math Toolboxを用いて実装しました!
今回はその取扱説明書や、クラス構造の詳細、代数的な理論というよりは寧ろ、MATLAB特有のクラスの使い方,実装テクニックにフォーカスしてMATLABクラスの実装例を紹介します。
はじめに
あかげふです。
MATLABアドベントカレンダー2024記事として投稿させていただきます。
鳥人間をしていたらもうB4になってしまいました。卒論で
「A,C,D 型量子群の微分演算子による実現とハイゼンベルグダブルの表現」
というテーマで考察内容を書いていて、その考察のために非可換代数の膨大な計算を必要としています。
今回紹介する計算機はそのために開発しました。
興味があれば連絡ください。
twitterでもこの計算機開発の進捗状況を発信しています。
@juvenile_crimes
シナリオ
非可換環の例としてリー代数の普遍包絡を挙げます(そういうモノがあるんだな程度でOK)。(他にも、行列の環、群環、リー代数、量子群などがあります。)
より具体的には、$U(sl_2 )$ はリー代数であり、 $E,F,H$ という3つの生成元からなる代数で
$$ [H,E]-2E=0,\quad[H,F]+2F=0,\quad[E,F]-H=0 $$
という3つの関係式から成ります。ここで $[X,Y]=XY-YX$ はリー括弧です。
さらに $\Delta (X)=1\otimes X+X\otimes 1,\quad\epsilon (X)=0\quad(X=E,F,H)$
という余積構造により双代数構造が入ります。
例えば、 $F^2 E^2 =E^2 F^2 -4EFH+2H^2 +2H$ という等式が出てきたとしましょう。これなら面倒くさいですが、定義関係式を何回か用いることで、できます。しかし、
$$ (F\otimes F^2 )(E\otimes E)=-2(H\otimes F)+2(H\otimes FH)-1(H\otimes EFF)+2(EF\otimes F)-2(EF\otimes FH)+1(EF\otimes EFF) $$
などになってくると、やりたくありません。
しかし、今回の計算機を使えば、次のようにチェックすることが出来ます:
-F^2*E^2+2*H +2*H*H -4*E*F*H +1*E*E*F*F
ans =
coeff base
_____ ____
0 1
-(F|F^2)*(E|E)-2*(H|F) +2*(H|F*H) -1*(H|E*F*F) +2*(E*F|F) -2*(E*F|F*H) +1*(E*F|E*F*F)
ans =
coeff base
_____ _____
0 1 ⊗ 1
このように計算機を使えば速くミスなくラクにチェック出来ます。
なぜMATLAB?
Mathematica,Maple,SageMath,GAPなど色々な非可換代数が扱えるツールが既に色々あります。特にSageはPython互換などの特徴があります。次のような理由からMATLABで実装しました:
- ライセンスの有無、Mathematicaはない、MATLABならある
- 数式処理機能(Symbolic)がある
- 自分で作ったほうが早いしクラスやOOP等の勉強になる
- 見た目や仕様を自分用にカスタマイズできるし見やすい
- 配列計算がサクッと書けるので、諸々の構文がスッキリする
- 実際の数式の見た目に近い形で(演算子オーバーロードにより)書ける
- インタラクティブに(コマンドウィンドウで)計算できる
Pythonでも同様のことは一応できますしSageMathと互換です。MATLAB大好きマンなので、Pythonに対するヘイトスピーチとの比較をしておくと、Numpyなど色々使わずとも(3),(4)が標準仕様で出来る(故にスッキリしている)ことがメリットです。
数式処理機能はあるものの、普通の(可換な)多項式や初等関数しか扱えないので、自分の用途である、非可換な演算子やq-exp、微分演算子の表現には不適格と判断し、このためのライブラリを制作したのが頑張りポイントです!
僕はMATLABに比べてC++やPythonの経験が無いですし、その他のツールも触ったことがないので、比較することは出来ません。
また、現状は無限和には対応できていません(残念)。一応、十分大きいNを取るなどして、なんとかなる範囲ではあります。
目的
非可換代数のインタラクティブな計算をサポートし、複雑な代数計算を派生的な実装含め容易に行えるようにする。
参考文献
全て公式ドキュメントで完結し、ネット上に公開されているので、リンクを適宜張ります。
まだ未完成なので今回の成果物のリポジトリはまだ公開していません。
(なので実装テクの紹介という形にとどめました。)
今回の制作物の紹介
冒頭にも説明した通り、行列の環、群環、リー代数、量子群など数学には様々な非可換代数のクラスをMATLABのsymbolic math Toolboxを用いて実装しました。それが"StrAlg"クラスです。これは加算,減算,乗算ができます。また、ホップ代数の余積,antipodeの計算も扱えます。
そこから派生させて、 $ワイル代数A_n ,\quadリー代数U(sl_2 ),\quad量子群U_q (sl_2 )$ のクラス(名前はそれぞれStrWeylAlg, Usl2, Uqsl2)を作りました。詳細は省きますが、それぞれの代数を関係式に従って簡約化する機能もあります。(たとえば $U(sl_2 )$ なら $EF-FE=H$ など)
ワイル代数が扱える、ということは微分演算子の代数を扱うことができます!
生成元と関係式の表示により代数は記述できるので、リー代数 $U=U(sl_2 )$ であれば、 $E,F,H$ という3つの生成元と次の関係式で定義出来ます:
$$ [H,E]-2E=0,\quad[H,F]+2F=0,\quad[E,F]-H=0 $$
PBWの定理により、任意の $U$ の元は $E^a F^b H^c (a,b,c:自然数)$ の形の項の線形結合で書けます。
よって、このような簡約化された形に書き直したいわけです。
クラス構造
StrWeylAlgを親クラス(スーパークラス)とし、ワイル代数やリー代数などはその子クラス(サブクラス)としました。これによりHopfAlgは抽象クラスで、双代数の演算の実装を子クラスに強制できます。(インターフェースとほぼ同義です。)
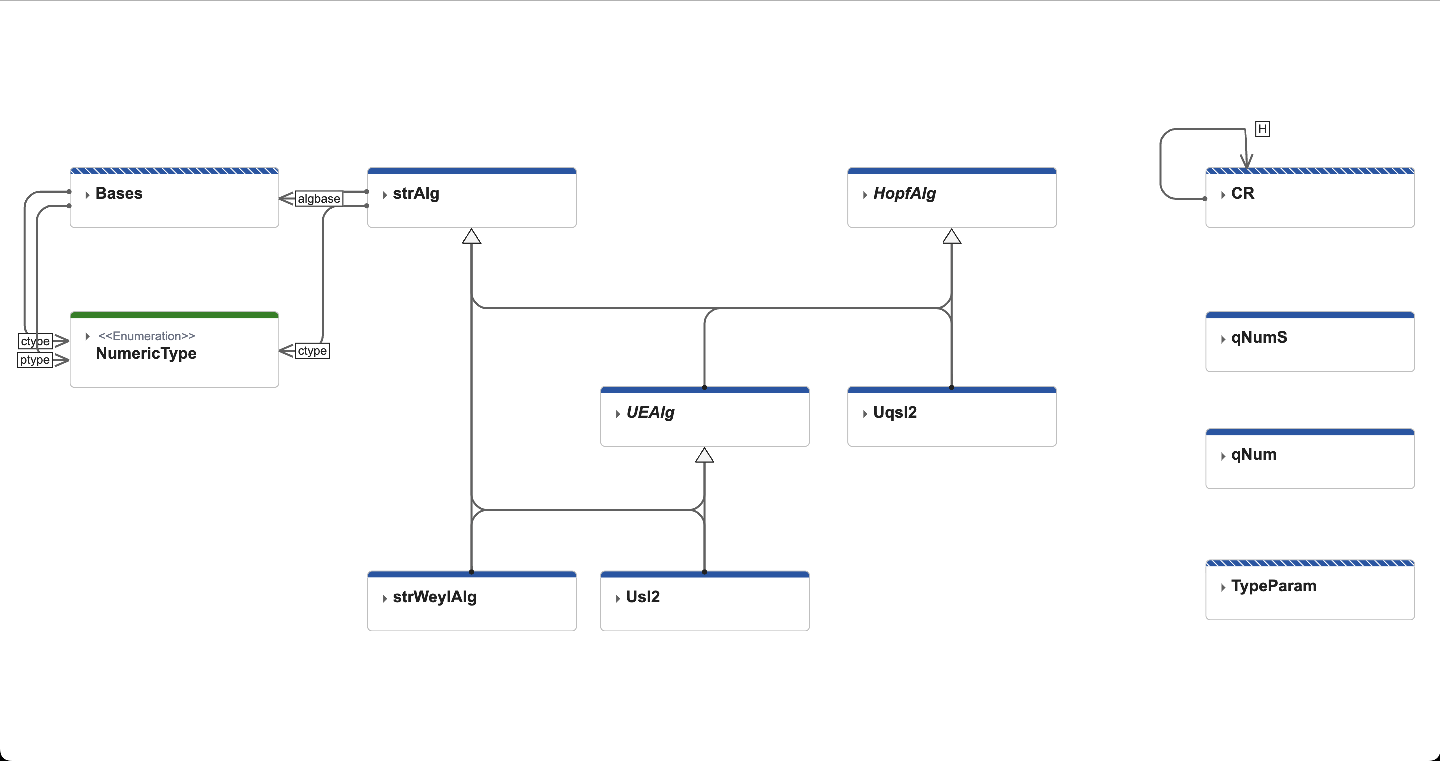
他に、計算ルールを定義するCRクラス(Calculation Ruleの略)、数学的意味の基底を定義するBasesクラス、q類似の計算をするクラスqNum等があります。
Uの実装例(フルのコード)
ソースコード
classdef(InferiorClasses=?sym) Usl2<strAlg&UEAlg
properties(Constant,Hidden)
B=Bases(3,["E" "F" "H"],"sl2")
end
%% generation
methods(Static)
function obj=make(cf,pw,~)
obj=Usl2().make@strAlg(cf,pw,Usl2.B);
end
function [O,E,F,H]=getGenerator(obj)
O=Usl2();
O=O.make(0,{[]});
E=O.make(1,{1});
F=O.make(1,{2});
H=O.make(1,{3});
end
end
methods
%% relation
function [rel,mlist,comm]=get2vRelation(obj)
persistent S
if isempty(S)
S=struct;
S.rel(1)=Usl2.make([1 -1 -1],{[1 2] [2 1] 3});
S.rel(2)=Usl2.make([1 -1 -2],{[3 1] [1 3] 1});
S.rel(3)=Usl2.make([1 -1 2],{[3 2] [2 3] 2});
S=obj.get2vRelation_(S);
S.comm={};
end
rel=S.rel;
mlist=S.mlist;
comm=S.comm;
end
end
end
strAlgのコード(要約)
要約ソースコード
classdef(InferiorClasses=?sym) strAlg
% Instance Properties
properties
cf (:,1) = 0 % Coefficients of the algebra elements
pw (:,:) cell = {[]} % Power arrays (exponents of basis elements)
bs (:,:) cell = {Bases.empty} % Bases corresponding to terms
ctype NumericType = "D" % Coefficient type
priority % Priority of basis elements
algbase (1,:) Bases % Base algebra for the elements
ZERO (1,:) cell % Represents the zero element
sortedFlag % Flags to indicate if terms are sorted
end
properties(Dependent)
% Dependent Properties
term % Number of terms
deg % Maximum degree of terms
basestr % String representation of basis elements
dims % Dimensions of the bases
rank % Rank (number of bases involved)
end
methods
% Arithmetic operations
function [i1, i2] = alignNum(i1, i2) % Align numeric types or symbolic types
function ret = casttype(obj, arg) % Cast input type to match the object's type
function ret = plus(i1, i2) % Addition for algebra elements
function ret = minus(i1, i2) % Subtraction for algebra elements
function i1 = uminus(i1) % Unary negation
function i1 = uplus(i1) % Unary positive (does nothing)
function ret = eq(i1, i2) % Equality check for algebra elements
function ret = mtimes(i1, i2) % Multiplication for algebra elements
function ret = lb(i1, i2) % Lie bracket computation
function [q, r] = mrdivide(i1, i2) % Division of algebra elements
function ret = mpower(i1, i2) % Power operation for algebra elements
function ret = unit(arg, rank) % Generate unit element of the algebra
function o = or(i1, i2) % Tensor product
function o = and(i1, i2) % Coproduct (not implemented)
function o = not(i1) % Coproduct computation (not implemented)
function o = prodeval(i1) % Evaluate product on algebra elements
% Algebraic calculations
function arg = calc(arg) % Simplification and zero removal
function obj = replace(obj, Ntimes) % Replace terms using relations
function obj = setSortedFlag(obj, flag) % Set sorted flag for terms
function ret = replace2v_(obj, Fidx) % Simplify terms based on 2-variable relations
function obj = removeZero(obj) % Remove zero-coefficient terms
% Verifications
function verify(obj) % Verify internal consistency of the object
function verifyBase(obj, pw, bs) % Verify base compatibility with power
% Object modifications and generation
function obj = make(obj, cf, pw, bs) % Create an algebra element with given properties
function obj = set_cp(obj, cf, pw, bs) % Set coefficients, powers, and bases
function ret = scalar(obj) % Generate a scalar algebra element
% Display methods
function ret = pol(arg) % Convert algebra element to polynomial form
function disp(i1) % Display the algebra object
function disp_(i1) % Helper for display
function disp0(i1) % Built-in display function
function ret = convertBaseString(obj, pw, arg) % Convert base and power to string
function disp1(arg) % Display as table
function disp2(arg) % Display as mathematical expression
function disp3(i1) % Display multiple terms
function ret = convertTermToSym(obj) % Convert terms to symbolic representation
function ret = sym(obj) % Convert entire object to symbolic expression
% Additional methods
function ret = ones(obj) % Generate ones for the algebra
function z = zeros(obj, varargin) % Generate zeros for the algebra
function ret = string(obj) % Convert algebra element to string
function ret = matrix(obj, i1) % Replicate algebra element into a matrix
function obj = setBase(obj, algB, Zero) % Set base and zero elements
function ret = subs(obj, varargin) % Substitute variables in the algebra object
% Properties
function ret = get.term(obj) % Get the number of terms
function ret = get.deg(obj) % Get the maximum degree of terms
function ret = get.dims(obj) % Get dimensions of bases
function ret = get.rank(obj) % Get the rank of the algebra
% Hidden methods
function ret = dimP(obj) % Get the dimension of power arrays
end
end
Uのテストスクリプト
テストスクリプト
% Define
[O,E,F,H]=Usl2.getGenerator;
A=O.make([3 2],{[] [1]});
B=O.make(3:4,{[] [2 3]});
I=O+1;
%% addition
A+B
C=A-B
A-A
O+A
A+3
4+A
%% multiplication
% lb(x,y)=[x,y]はLie bracket
F*E*2
assert(H^2*F-4*F+4*F*H-F*H*H==O)
F^3*H^2*E^2
% カシミール作用素は中心に属する
assert(lb(E^3*F*H*F*E^3,F*E+E*F+H^2*(1/2))==0)
%% TensorProduct
% テンソル積は縦棒 | で記述する。
% テンソル積 | より+,-の演算子のほうが優先度が高いので注意する。
-(H|F)+(F*E|F)
(F|F)*(E|E)
lb(H|H,E|F)
(1|E)+(E|1)
1|E+E|1 % 1⊗(E+E⊗1)と解釈されてエラーの可能性もある
%% comutiplication
assert(Delta(A*B)-Delta(A)*Delta(B)==0)
assert(counit(E*F+E)==0)
C=Delta(B*A);
idx=cellfun(@length,C.pw(:,1))==0;
C2=C.make(C.cf(idx),C.pw(idx,2));
assert(C2-B*A==0)
実際の使用例
説明書(暫定)の抜粋です。細かく見る必要はないので、雰囲気だけ。
使用例
Define
生成元を定義する
[O,E,F,H]=Usl2.getGenerator;
Construct
係数と生成元の番号を入力する
A=O.make([3 2],{[] [1]})
A = +3*1 +2*E
B=O.make(3:4,{[] [2 3]})
B = +3*1 +4*F*H
add
A+B
ans = +6*1 +2*E +4*F*H
C=A-B
C = +2*E -4*F*H
A-A
ans = +0*1
O+A
ans = +3*1 +2*E
A+3
ans = +6*1 +2*E
4+A
ans = +7*1 +2*E
multiply
lb(x,y)=[x,y]はLie bracket
F*E*2
ans = -2*H +2*E*F
assert(H^2*F-4*F+4*F*H-F*H*H==O)
F^3*H^2*E^2
ans = -96*F*H +96*E*F*F +48*F*H*H -48*E*F*F*H +42*F*H*H*H +16*E*E*F*F*F -42*E*F*F*H*H +6*F*H*H*H*H +8*E*E*F*F*F*H -6*E*F*F*H*H*H +1*E*E*F*F*F*H*H
カシミール作用素 $EF+FE+\frac{1}{2}H^2$ は中心に属する
lb(E^3*F*H*F*E^3,F*E+E*F+H^2*(1/2))
ans = +0*1
TensorProduct
テンソル積は縦棒 | で記述する。
テンソル積 | より+,-の演算子のほうが優先度が高いので注意する。
-(H|F)+(F*E|F)
ans = -2*(H|F) +1*(E*F|F)
(F|F)*(E|E)
ans = +1*(H|H) -1*(H|E*F) -1*(E*F|H) +1*(E*F|E*F)
comutiply
$$ \Delta (EF)-\Delta (E)\Delta (F)=0 $$
disp1(Delta(E*F)-Delta(E)*Delta(F))
coeff base
_____ _____
0 1 ⊗ 1
$$ \Delta (E^3 ) $$
disp1(Delta(E^3))
coeff base
_____ _________
1 1 ⊗ E E E
3 E ⊗ E E
3 E E ⊗ E
1 E E E ⊗ 1
内部計算の実装と計算アルゴリズムの概説
関係式を用いた簡約化がメインの計算アルゴリズムです。
内部ではStrAlgオブジェクトは次の対応関係で表されています:
| 生成元 |
自然数のラベル |
| 単項式 |
ラベルの配列 |
| 多項式 |
ラベル配列の縦方向のセル配列 |
| テンソル積因子 |
セル配列の横方向の配列 |
また、関係式は0と等しいStrAlgオブジェクトの配列で表されます。
単項式の次数が揃っていないので、複数項を扱う場合はジャグ配列となるので、内部的にはセル配列を使っています。
また複数のテンソル積因子に対応するため、テンソル積因子の配列を横方向に並べた2次元セル配列を使っています。
簡約化は、各項の単項式の次数が辞書式で昇順になるように、関係式を使いながら単項式をいわばバブルソートして、簡約化していきます。
たとえば $U(sl_2 )$ の場合、E:1 . F:2 , H:3という順番になるように簡約化していきます。
FEという項は、配列が[2 1]なので、[1 2]となるように簡約化します。
それで、 $FE=EF-H$ という関係式を検索して、適用します。
MATLABコーディングテクニックs
ここからは実装に実際に使ったテクニックを紹介していきます。
公式ドキュメントにクラスの仕様は全て書いてありますが、どう使えば良いかの実例はあまりネット上には転がって居なかったり、参照の概念が無い、といった頓珍漢なことを解説してたり、便利な機能が埋もれていたり...
グローバル変数の代替案(ハンドルクラスの使用)
グローバル変数を使うなとよく怒られます。しかし、
「関数の挙動を設定によって変えたいけど、いちいち引数に渡すのは面倒」
のように、どうしても使いたくなる場面があるときのベストプラクティスはあまり知られていない気がします。でもハンドルクラスを使えば解消できます!
より具体的に問題を見ます。計算結果に対して色々な表示方法があります。たとえば $FE=EF-H$ であれば
disp1(F*E)
coeff base
_____ ____
-1 H
1 E F
disp2(F*E)
-1*H +1*E*F
など、数式っぽいスタイル(2)か、項別に整理されたスタイル(1)があります。
それぞれメソッドdisp1、disp2が対応していて、その実装方法は後述します。
MATLABはコマンドウィンドウで結果を返すと、そのオブジェクトのdispメソッドが呼ばれます。このとき、
disp(obj,displayRule)
のように、displayRuleという引数は渡せません。昔の僕だったらglobalに頼っていました。でもハンドルクラスを使うことでこの問題は解消できます。
まずdispメソッドをオーバーライドして、そのクラスの表示の挙動をカスタマイズできます。以下が、StrAlgクラスのdispメソッドです。
function disp(arg)
% CR.H.displayRuleに従って結果を出力
feval("disp"+CR.H.displayRule,arg);
% (本当は空配列など分岐処理があるが、本筋でないので省略)
end
このようにCR.H.displayRule=1,2を参照することでargの表示方法を切り替えます。
そして、このCRクラス(CalcRule)は、ハンドルクラスです:
classdef CR<handle& matlab.mixin.CustomCompactDisplayProvider ...
& dynamicprops& matlab.mixin.SetGet
%CR Calculation Rules
properties(Constant)
H CR=CR
end
properties
displayRule=1
end
end
型制約(後述)を見れば分かるとおり、クラスCRのプロパティHにCR自身のオブジェクトがConstantとして入ります。デフォルトでMATLABは値クラスなので、ハンドルクラスと指定しないとこのような入れ子は許容されません。
ハンドルとすることで、クラスに対して一意的に定まるオブジェクトCR.Hが定義されます。これにより、一意的なdisplayRuleを定義できるわけです。
dispメソッドで実際に使う場合は上のコードのように、CR.H.displayRuleで表示規則にアクセスして表示を実行します。また、変更する際は
set(CR.H,displayRule=2)
を実行することで、変更出来ます。
警告
CR.H.displayRule=2 % NG
これはCR.Hという構造体を定義する構文になってしまいます。
そのためにSetGetメソッドを導入しています(matlab.mixin.SetGet)
なお、表示をカスタマイズする以前のデフォルトの表示もクラスのデバッグ等で必要なので、これもdisp0メソッドとして定義します。
disp0(F*E)
Usl2 のプロパティ:
cf: [2x1 double]
pw: {2x1 cell}
bs: {2x1 cell}
ctype: D
priority: 3
algbase: [1x1 Bases]
ZERO: {[1x1 Usl2]}
sortedFlag: [2x1 logical]
term: 2
deg: 2
dims: 3
rank: 1
builtinで組み込みメソッドを呼べます。
function disp0(arg)
builtin("disp",arg)
end
- Handle Classes Overview:https://jp.mathworks.com/help/matlab/handle-classes.html
-
Customizing
dispMethod :https://www.mathworks.com/help/matlab/matlab_oop/displaying-objects-in-the-command-window.html - Overloading Functions in MATLAB Classes:https://jp.mathworks.com/help/matlab/matlab_oop/overloading-functions-for-your-class.html
- Behavior of Handle Objects:https://jp.mathworks.com/help/matlab/matlab_oop/handle-objects.html
Symbolic計算
詳細は省きますが、
$$ -\frac{q}{q^2 -1}K+\frac{q}{q^2 -1}K^{-1}+EF $$
のように、qという変数の有理関数係数の代数を考える場合があります。そのような場合でも同様に計算するため、symbolic math toolboxを用います。
ただsymbolicのオブジェクトを自分の意のままに操作するのは難しいです。
childメソッドを使って、要素ごとに分解することは一応可能ですが、どう分解されていたか、の情報が抜け落ちる(出力できない)ので、あまり有用とは言えません。
目的のためには単項式を明確に記述する必要があるのと、計算パフォーマンスの観点から、StrAlgクラスは係数以外のロジックではsymbolic計算を使っていません。
しかし、q類似に関する計算は可換ですし、因数分解もできるので、量子群の計算において実力を遺憾なく発揮します。
そこが一番の工夫点であり、非可換計算におけるsymbolicの進歩と言えます。
プロパティ、メソッドのサイズ、型制約
MATLABでは、プロパティの型制約を指定することができます。これにより、プロパティの型を間違えて代入するミスを防ぐことができます。
例えば、次のような準同型写像の関数を考えます。
function ret=algfun(obj,funs,units)
% algfun 代数準同型の作用
% funs,unitsをテンソル階数の分だけ繰り返し入力する
% funs:具体的にはstrAlg().algIDで返される関数形
% funs:(power,base)→stralg
% units
arguments
obj (1,1) strAlg
end
arguments(Repeating)
funs (1,1) function_handle
units (1,1) strAlg
end
% 実装略
end
このとき、funsは関数ハンドル、unitsは単位元(strAlgクラスのオブジェクト)である必要があります。
このように型制約を指定することで、関数の引数の型を間違えて代入するミスを防ぐことができます。
また、サイズもスカラー、という制約を指定することができます。
これにより、ベクトルオブジェクトを代入するミスを防ぐことができます。
- Property Size and Class Validation:https://jp.mathworks.com/help/matlab/matlab_oop/property-size-and-class-validation.html
- Property Validation Functions:https://jp.mathworks.com/help/matlab/matlab_oop/validate-property-values.html
- Defining Properties in MATLAB Classes:https://jp.mathworks.com/help/matlab/matlab_oop/defining-properties.html
演算子オーバーロード
MATLABでは、演算子オーバーロードを使うことで、自作クラスに対して演算子を定義することができます。
例えば、次のような演算子を定義します:
function ret = mtimes(i1, i2) % Multiplication for algebra elements
これにより、i1*i2の演算が自作クラスに対して定義されます。
他にも、+,-,*,/などの演算子を定義することができます。
テンソル積は残念ながらなかったので、|演算子(tensorのorの部分)として定義しました。
また、1+Eのように1はdouble型であるため、普通はstrAlgクラスのオブジェクトとの演算ができません。これを可能にするために、double型をstrAlgクラスのオブジェクトに変換するメソッドcasttypeを定義しました。クラスが異なる場合、自動的に変換することができます。
また、メソッドが呼ばれる優先順位の関係で、symbolic数との演算を行うとエラーが出る問題があります。たとえばsymbolic変数qとstrAlgクラスのオブジェクトAに対して、q*Aという演算を行うと、symクラスのメソッドmtimesが先に呼ばれてしまいます。これを防ぐために、InferiorClasses=?symというオプションを指定しました。
-
Overloading Functions in Class Definitions:https://jp.mathworks.com/help/matlab/matlab_oop/overloading-functions-for-your-class.html
-
Operator Overloading:https://jp.mathworks.com/help/matlab/matlab_oop/implementing-operators-for-your-class.html
-
Object Precedence in Expressions:https://jp.mathworks.com/help/matlab/matlab_oop/object-precedence-in-expressions-using-operators.html
クラスビューワーアプリ
MATLABでは、クラスビューワーアプリを使うことで、クラス図を作成することができます。
これにより、クラスの関係を視覚的に理解することができます。
クラスビューワーアプリは、MATLABの標準アプリケーションの中にあります。
クラスビューワーアプリを使うことで、クラス図をGUI形式で手軽に自動生成できます。
配置を手直ししたら、先程のクラス図が完成です。
プロジェクト
MATLABでは、プロジェクトを使うことで、関連するファイルを一元管理することができます。
Gitとの連携も可能です。研究室でのコード共有や自分の進捗管理に使用しています。
パスの設定やファイルの整理が簡単にできるので、効率的に作業することができます。
「プロジェクトパスに追加」を使うことで、プロジェクト内のファイルをプロジェクト起動時に自動的にパスに追加することができます。
setup.mを使うことで、プロジェクト起動時に自動的にスクリプトを実行することができます。(これで自動的に計算規則の設定ができます。)
初期作業フォルダを設定し、startup.mでプロジェクトを起動すればMATLAB起動時に自動的にプロジェクトが開かれるので便利です。
- Creating Projects:https://jp.mathworks.com/help/matlab/matlab_prog/create-projects.html
- automate startup and shutdown of Projects:https://jp.mathworks.com/help/matlab/matlab_prog/automate-startup-and-shutdown-tasks.html
- Managing Projects:https://jp.mathworks.com/help/simulink/project-management.html
- Using Projects for Continuous Team Development (Video):https://www.mathworks.com/videos/continuous-team-development-using-project-1638877903151.html
入れ子関数のオブジェクトによる線形作用の記述
ここがMATLABの特徴的な記述方法です。関数の引数に関数を渡す関数ハンドルとcellfunを用いた一括計算を組み合わせることで、線形作用を簡潔に記述することができます。
例えば乗算メソッドmtimesの実装は次のようになります:
function ret=mtimes(i1,i2)
R=i1.rank;
ret=lfun_(i1|i2,@fun);
function [c,p,b]=fun(p,b)
c=1;
p=cellfun(@(p1,p2){[p1 p2]},p(1:R),p(R+1:end));
b=cellfun(@(b1,b2){[b1 b2]},b(1:R),b(R+1:end));
end
end
内部的にはStrAlgクラスではA=EF , B=H^2であれば、A,Bの積はEFという文字列とHHという文字列を結合して、EFHHという文字列を作ります。
それを線形に拡張することで演算を行います。そのとき、線形作用lfunメソッドを実装しておき、線形作用する関数をfunとして渡すことで、線形作用を実現しています。
実際にはテンソル積の計算があるので、もっと複雑ですが、それぞれのテンソル因子に対して文字列の結合を行います。
"各テンソル因子に対して"、という日本語の表現がそのままMATLABのコードとしてcellfunになっているのが特徴です。
これにより、日本語の表現とMATLABのコードが一致しているので、コードの理解が捗ります。
- Function Handles:https://jp.mathworks.com/help/matlab/function-handles.html
-
cellfunFunction :https://jp.mathworks.com/help/matlab/ref/cellfun.html
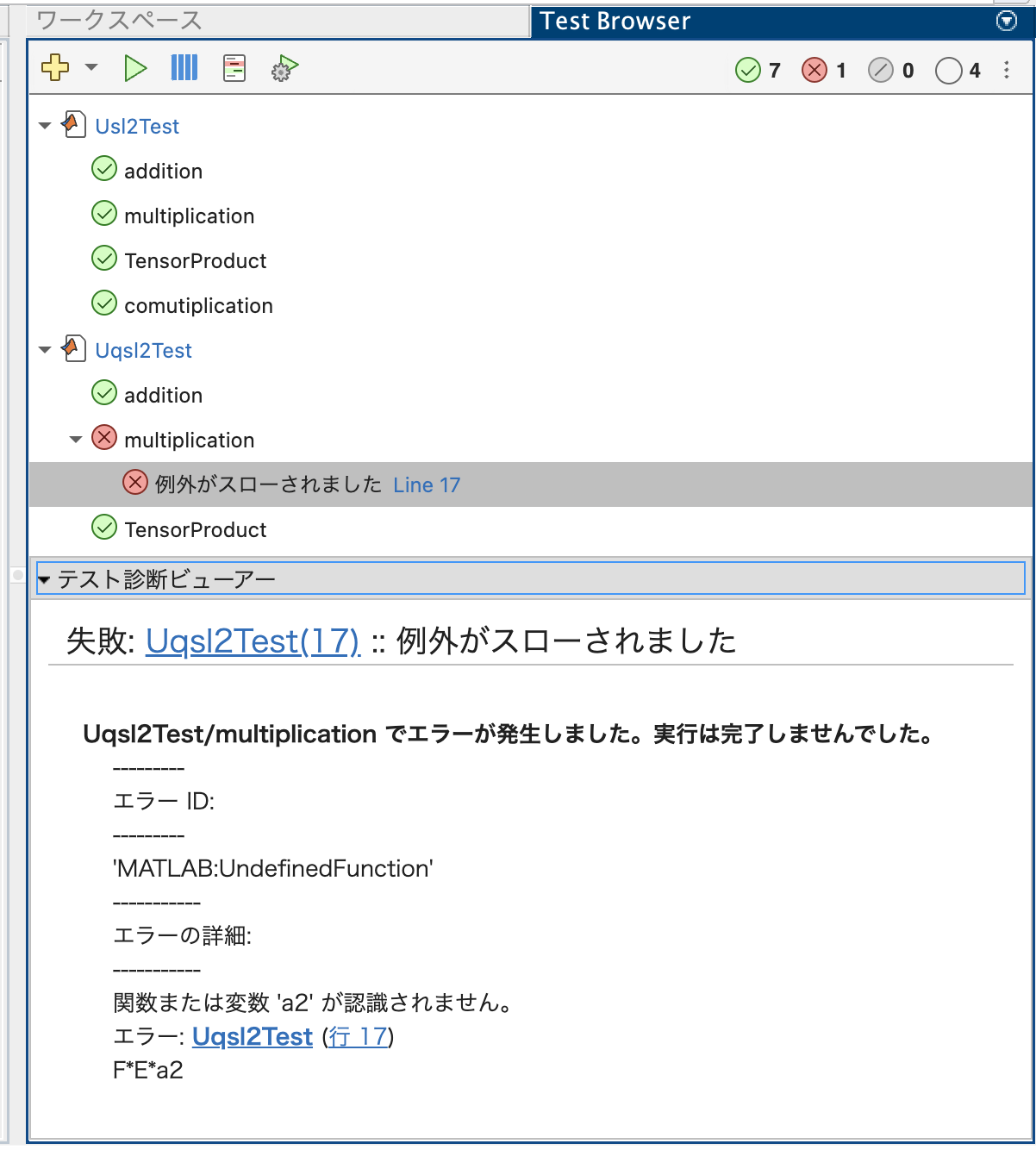
テストスクリプト
テストのソースコードのように、スクリプト形式でテストコードを記述することができます。
標準MATLABアプリのテストアプリを使うことで、テストスクリプトを視覚的に実行することができ、実装の確認やデバッグが捗ります。
- Writing Script-Based Unit Tests:https://jp.mathworks.com/help/matlab/matlab_prog/write-script-based-unit-tests.html
- Testing Apps:https://jp.mathworks.com/help/matlab/test-apps.html
表示メソッドのカスタマイズ
実装効率の観点から、table形式で表示するdisp1メソッドと、string形式で表示するdisp2メソッドを実装しました。
num2str関数やsymのlatexメソッドによりstringに変換しています。
stringだと余計な引用符""がついてしまうので、categorical配列を変に?使うことで、引用符が無い形で表示することができます。
- Custom Display Interface:https://jp.mathworks.com/help/matlab/matlab_oop/custom-display-interface.html
-
num2strFunction :https://jp.mathworks.com/help/matlab/ref/num2str.html -
LaTeX Representation of
symObjects :https://jp.mathworks.com/help/symbolic/sym.latex.html
ライブスクリプトの常識
本記事はライブスクリプトを用いてMATLABエディタ上で作成されています。
コードセルとテキストセルが混在したPythonのノートブックのような形式で、コードとその説明を同時に記述することができます。
markdown形式やLaTeX形式にエクスポートすることもできるので、それをQiitaにほぼそのまま貼り付けて、このような記事を作成することができます。
- Creating Live Scripts:https://jp.mathworks.com/help/matlab/matlab_prog/create-live-scripts.html
- Live Script to Markdown Conversion for Qiita (External Reference):https://qiita.com/eigs/items/513a17bd8cb2c5c5f435
でも、なんかR2024aにおいて、イメージ画像を貼り付けたらmarkdownのスクスポートがバグるのは僕だけですか?
へんなバックスラッシュが付く箇所があるので、そこはスクリプトを書いて自動削除するようなものを書きました。
今後の展望
-
今は困ってないですがsageMathなどとの互換性を持たせたら既存の代数に関する理論を使えると思います。
-
MEX化による計算パフォーマンスの改善も見込めます。
-
他の色々なリー代数の実装や微分演算子による表現の構成にもどんどん使っていきたいと思います(今執筆中の卒論の内容)
-
エラーハンドリングが現状手薄ですが、(自分は把握できてるが)面倒なので需要次第で対応したいです。
-
関係式の適用の部分のアルゴリズム的改善もあるかもしれません。(非可換)グレブナー基底の理論を適用できるのかは、僕の理解が足りません。
-
無限和の形式的な評価($\Sigma_{n>0} E^n$のようにダミー変数$n$の和の計算ができるようにするなども、一応出来る方法は思いついていますが、手計算のほうが正確で、実装が面倒なので、後回しです。
-
現状、係数体にはsymbolicまたはdoubleを入れますが、strAlgを入れ子にして、高効率にq類似の処理も行ってみたいです。
-
bialgebroidの計算も載せてみたいです。
リポジトリ公開について
- 取扱説明書を付けてリポジトリを公開したいモチベもあります。(使ってみたい、と直接言及してくだされば励みになります。)
興味があれば連絡ください。