対象読者
- データ分析や機械学習の初学者
- 時系列予測や需要予測を扱っている人
- 統計学や数式に興味がある人
執筆の背景
私は普段の仕事の1つで、機械学習(ML)を使った時系列モデルでの需要予測に取り組んでいます。
時系列予測は奥が深く、目的変数(需要量)の分布や外生要因(新型コロナウイルス感染拡大)などを良く考えて機械学習モデルを構築する必要があります。
仕事の中で、最適化指標(MLトレーニング時の評価関数)の違いによって、予測傾向が大きく変わり、プロジェクトがスムーズに進む場面に遭遇する機会がありました。自戒の意味もこめてMAEとRMSEの違いについて改めて詳しく解説しようと思いました。
前提条件
- MLによる時系列モデルによって商品の需要量を予測する
- 過去の需要をもとに、先半年間の需要を予測する
- 日別の需要量を予測して欲しいという要望、ただし、現場では月単位の合計の需要量を生産管理などに活用する
MAEとRMSEの違いについて
平均絶対誤差(MAE: Mean Absolute Error)
MAEは予測値と実測値の差の絶対値の平均を表す指標です。
$$ MAE = (1/n)Σ|y_i - ŷ_i| $$
実測値(yi)と予測値(ŷi)の差分に対して絶対値をとった後に相加平均をとります。
MLの最適化指標として使う場合は、目的変数の分布によらず誤差を均一に扱うため、外れ値の影響をあまり受けない予測を出したい時に効果を発揮します。
二乗平均平方根誤差(RMSE: Root Mean Square Error)
RMSEは予測値と実測値の差を二乗して平均を取り、その平方根を計算した指標です。
$$ RMSE = √((1/n)Σ(y_i - ŷ_i)²) $$
二乗誤差の相加平均を計算した後に平方根をとるのがミソであり、分布の最頻値から離れた値では誤算のペナルティが大きく、最頻値に近い(誤差が比較的小さい)場所にある誤差は大きな誤差の影響に埋もれやすくなります。
正規分布に近い分布や外れ値の影響も含めて予測したいような場合に効果を発揮します。
MAE→RMSEに最適化指標を変更
改めて今回のプロジェクトの前提条件を確認すると、
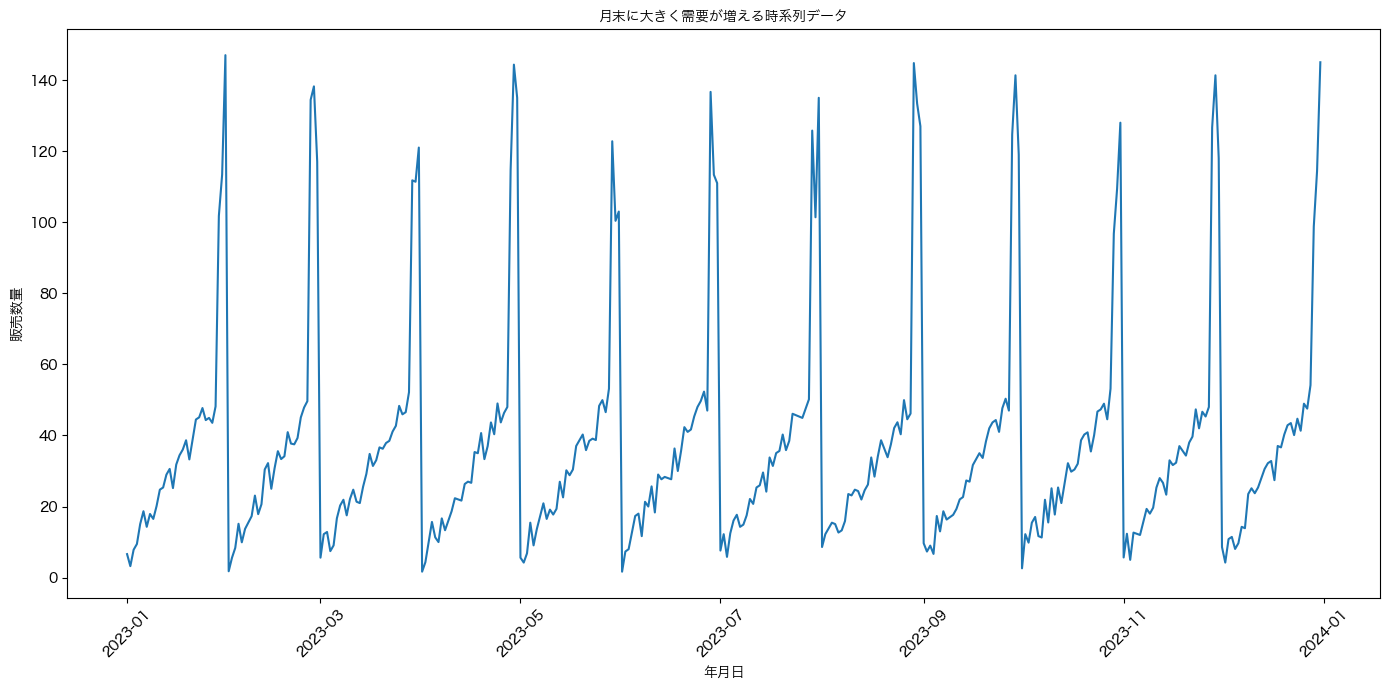
「日別の時系列予測モデルを組んで欲しいが、現場の生産管理に使うのは月別の合計予測値」という少し特殊な事情があります。
また、高価な商品や嗜好品などの需要予測では良くあることなのですが、目的変数(需要量)の月ごとの分布を分析すると、月末にかなり極端な大きな需要の盛り上がりがありました。
消費者目線に立って考えると予想できるのですが、高価な商品や嗜好品は給料日後や月末のご褒美として購入される方が多いと考えられます。
今回のプロジェクトでは、外れ値の影響を受けにくいようにMAEを最適化指標としてモデルを構築していました。
しかし、月末の盛り上がりによる高い外れ値の影響は無視されやすくなる(厳密には外れ値ではない)ため、過小気味の予測を出してしまうという問題がありました。この状態で月別の予測値を集計すると、常に少し過小気味に予測してしまう現場では使いにくいモデルになっていました。
このケースでは最終的に評価指標をRMSEに変更することで、予測モデルの過小予測傾向がなくなり、予測精度を大幅に改善することができ。
MAEとRMSEの特徴を踏まえた利用方法
MAEの特徴
- 外れ値の影響を受けにくい
- 誤差の大きさに比例したペナルティ
- 解釈が直感的で分かりやすい
RMSEの特徴
- 大きな誤差に対して二乗のペナルティ
- 外れ値に敏感
- 予測精度の改善が必要な箇所の特定に有効
ビジネス要件に基づく選択
- 大きな誤差を重点的に改善したい場合:RMSE
- 全体的な予測精度を均等に評価したい場合:MAE
データ特性による選択
- 外れ値が多いデータ:MAE
- 正規分布に近いデータ:RMSE
モデルの用途による選択
- 異常検知:RMSE
- 一般的な予測タスク:MAE
終わりに
今回はMAEとRMSEについて、実際に現場で発生する課題感を踏まえて記事にしました。機械学習を始めると最初に学ぶ最適化指標ですが、数式の意味を踏まえてしっかりと理解して使いこなせば良い予測モデルを構築する手助けとなります。時系列予測はかなり奥が深いので、解説して欲しい内容などあればコメントでいただけると嬉しいです。
(記事中誤った説明をしている部分があれば、コメントでご指摘いただけると幸いです。)