【Python】ローパスフィルタで波形のノイズを除去する

Numpy の fft を用いて、ローパスフィルタで波形のノイズを除去します。前半部分はサンプル波形の生成、後半部分でノイズ除去の処理をしています。

qiita.rb

# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
import math
import copy

# 波形からノイズを除去する。
# 前半：波形生成
# 　　　２つの周波数のcos波とランダムノイズの足し合わせ
# 後半：ノイズ除去
# 　　　元波形　　　f　元波形のfft　F
# 　　　処理後波形　g　処理後波形のfft　G
#
# 正規化とアンチエリアジングをやめて、
# 共役複素数の項を残すことにしました。18.12.05

def main():
    # データのパラメータ
    N = 40000             # サンプル数
    dt = 1*1e-5           # サンプリング間隔

    # 軸の計算    
    t = np.arange(0, N*dt, dt) # 時間軸
    freq = np.linspace(0, 1.0/dt, N) # 周波数軸

    # サンプル波形のパラメータ
    a = 10                # 交流成分
    fq1, fq2 = 25, 50     # 周波数
    phi1, phi2 = 0, 30    # 位相
    pi = math.pi          # π
    phirad1, phirad2 = phi1*pi/180, phi2*pi/180  # 位相ラジアン

    fc = 200         # カットオフ周波数
    fs = 1 / dt     # サンプリング周波数
    fm = (1/2) * fs # アンチエリアジング周波数
    fc_upper = fs - fc # 上側のカットオフ　fc～fc_upperの部分をカット

    # 時間信号を生成（周波数f1の正弦波+周波数f2の正弦波+ノイズ）
    noise = 0.5 * np.random.randn(N)
    f = a + 1*np.cos(2*np.pi*fq1*t+phirad1) \
          + 1*np.cos(2*np.pi*fq2*t+phirad2) \
          + noise

    # 元波形をfft
    F = np.fft.fft(f)

    # 正規化 + 交流成分2倍
    # F = F/(N/2)
    # F[0] = F[0]/2

    # アンチエリアジング
    # F[(freq > fm)] = 0 + 0j

    # 元波形をコピーする
    G = F.copy()
    
    # ローパス
    G[((freq > fc)&(freq< fc_upper))] = 0 + 0j

    # 高速逆フーリエ変換
    g = np.fft.ifft(G)

    # 振幅を元に戻す
    # g = g * N

    # 実部の値のみ取り出し
    g = g.real

    # プロット確認
    plt.subplot(221)
    plt.plot(t, f)

    plt.subplot(222)
    plt.plot(freq, F)

    plt.subplot(223)
    plt.plot(t, g)

    plt.subplot(224)
    plt.plot(freq, G)
    
    plt.show()

if __name__ == "__main__":
    main()

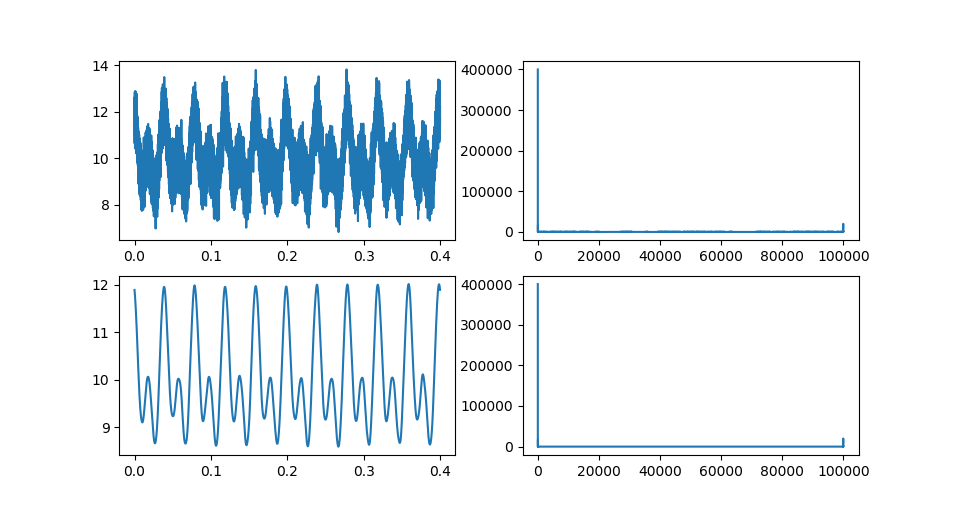
処理結果
上段　処理前　（波形とスペクトル）
下段　処理後　（波形とスペクトル）