[競プロ]いもす法実装【Java】

いもす法を解きます

いもす法とは

領域内の加算を効率的に行うアルゴリズムです。多次元でも行えて、便利なアルゴリズムとされています。累積和と関連があります。参考リンクは以下のとおりです。

例題に合わせて解説

ABC035 - C オセロ
ここでは例題に合わせて解説していきます。
今回、オセロのN個の駒が黒を上にして一列に置かれています。その後、Q回、ある駒からある駒までを裏返すという操作をします。その結果を一列で出力せよ、という問題です。

今回の制約からN,Qは200,000までで、例えばN=Q=200,000であったとし、各QにおいてN個の駒を裏返すという操作をするとすると、愚直に実装した場合、O(NQ)の計算量が必要となり、TLEとなってしまいます。
そこでいもす法の登場です。

今回は例題に合わせt１次元の領域について考えます。いもす法では、領域の両端のみ考え、後で累積和を取った際に操作の結果の配列となるよう調整しています。

以下の配列について考えます。

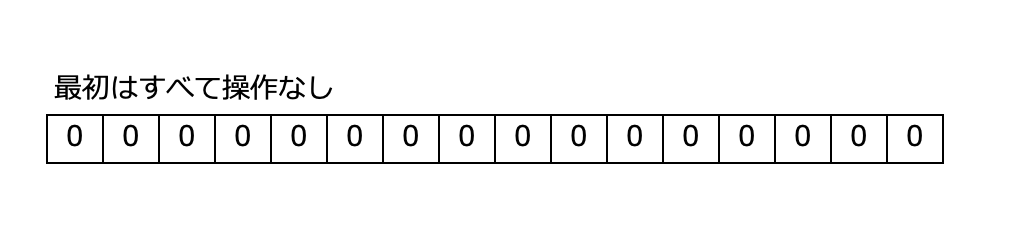
Integerの配列を作成してすべて0（一度も操作されていない）とします。
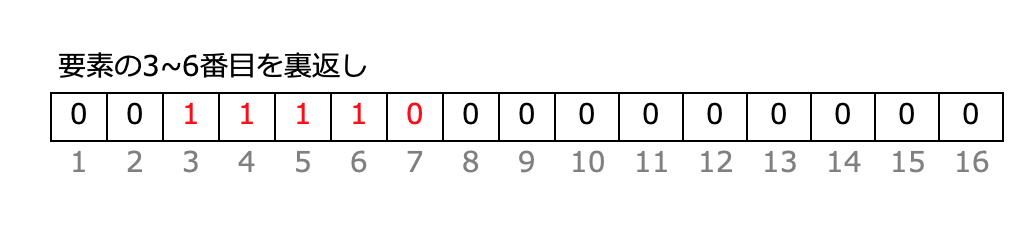
ここで、配列の3~6番目に操作（今回の例題に合わせると、裏返し）があったとしましょう。
以下のように、3番目に1を、7番目（6+1番目）を　-1で更新します。

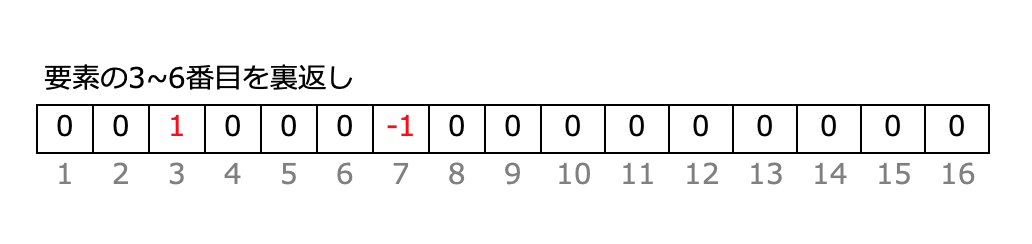
この配列は、累積和を取ると以下のような配列になります。
3~6番目を裏返していますね。

このように、配列の操作する要素すべてにアクセスするのを最後に累積和するときだけにして、それ以外では始点と終点にしかアクセスしなくて良い、というのがいもす法の効率の良いところです。

ちなみに、今回の問題ではいもす法により該当の要素が何回裏返したのかという情報を保持しておいて、奇数回であれば白、偶数回であれば黒として答えを出しています。

ACコード

Main.java

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt(); // 駒数
        int q = sc.nextInt(); // クエリ数

        int[] array = new int[n + 1]; // 駒の配列
        int[] ruisekiArray = new int[n + 1]; // 累積和とった配列

        for (int i = 0; i < q; i++) {
            int l = sc.nextInt() - 1; // 0-indexed
            int r = sc.nextInt() - 1; // 0-indexed

            // いもす法で、lに1を足してr+1から1を引く
            array[l]++;
            array[r + 1]--;
        }

        // arrayの累積和をとる
        ruisekiArray[0] = 0;
        for (int i = 1; i <= n; i++) {
            ruisekiArray[i] = ruisekiArray[i - 1] + array[i - 1];
        }

        // 偶数回裏返っていたら0, 奇数回であれば1とする
        for (int i = 1; i <= n; i++) {
            if (ruisekiArray[i] % 2 == 0) {
                ruisekiArray[i] = 0;
            } else {
                ruisekiArray[i] = 1;
            }
        }

        // 出力
        StringBuilder sb = new StringBuilder("");
        for (int i = 1; i <= n; i++) {
            sb.append(ruisekiArray[i]);
        }

        System.out.println(sb.toString());

    }
}

//