記事の概要
自分の勉強兼メモでまとめている記事シリーズです。
こちらの記事の続きです。
javaでアルゴリズム入門 - 探索編(全探索、二分探索)
今回の記事では
- 深さ優先探索
について勉強します。前回の記事の続きのノリで書いています。
深さ優先探索
ここからもうなんですかこれって感じですが進めましょう。学びつつまとめつつ。
深さ優先探索です。
DFS(depth-first-search)とも呼ばれるらしいですね。そういえば良くこの単語見ますね。
深さ優先探索、幅優先探索は木やグラフの探索に有用らしいですね。木やグラフの説明は割愛でいきます。
以下に図を載せます。(wikipediaより)
こんな順番で木を深さ優先で探索していくのがDFSみたいですね。
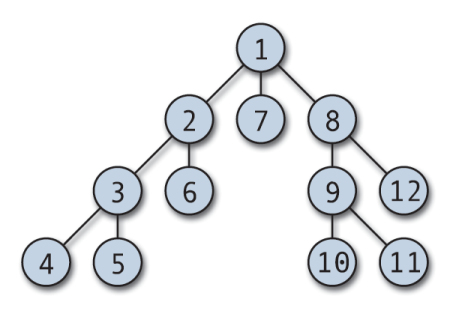
「なにが深さ優先なのかわからないよ!」と言う方は幅優先探索の探索順を見ていただければ一発だと思います。
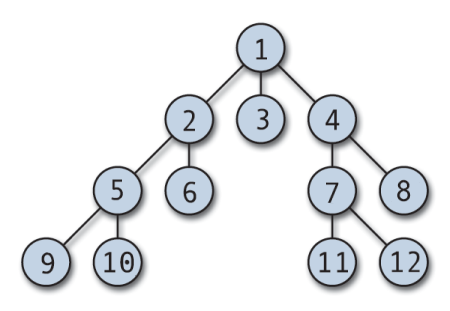
番号の違いが分かりましたか?
深さ優先探索は、根から子を持たないノードまで一直線で探しにいっていて、幅優先探索は一旦根から深さ1のノードを順番に探索に行ってます。
ちなみに実装方法としては2種類あるそうです。
- スタック(後入れ先出しのデータ構造)を使う方法
- 再帰関数を使う方法
・・・ぶっちゃけだからなんやねんって感じです。例を見なければよく分かりませんね。
と思って簡単な例を探してみたらなかなか直感的にわかる例ってないのですね。。
上図の通り、ただ単にそういう順番に探索していくやり方だよ!って感じなのですかね。
問題例を見て解きながら理解していくことにします。理解できたら簡単な例が作れるかも?
問題文・入力例などはここをクリックして表示
※できるだけ問題リンクを参照してください
(セクション開始)
【問題文】
とある所に島国がありました。島国にはいくつかの島があります。このたび、この島国で埋め立て計画が立案されたのですが、どこを埋め立てるか決まっていません。できることなら埋め立てによって島を繋いで、1つの島にしてしまいたいのですが、たくさん埋め立てるわけにもいきません。
10マス × 10マスのこの島国の地図が与えられるので、1マスを埋め立てた時に 1つの島にできるか判定してください。ただし、地図で陸地を表すマスが上下左右につながっている領域のことを島と呼びます。
【入力】
入力は以下の形式で標準入力から与えられる。
\(A1,1\)\(A1,2\)...\(A1,10\)
\(A2,1\)\(A2,2\)...\(A2,10\)
:
\(A10,1\)\(A10,2\)...\(A10,10\)
島国の地図が 10行にわたって与えられる。
各行は 10文字からなり、o は陸地を、x は海を表す。
少なくとも 1マスは陸地があることが保証される。
少なくとも 1マスは海があることが保証される。
【出力】
海を 1マスだけ陸地にすることで全体を 1つの島にできるなら YES 、できないなら NO を出力せよ。出力の末尾には改行をつけること。ただし、元から 1つの島だった場合も YES を出力せよ。
【入力例】
xxxxxxxxxx
xoooooooxx
xxoooooxxx
xxxoooxxxx
xxxxoxxxxx
xxxxxxxxxx
xxxxoxxxxx
xxxoooxxxx
xxoooooxxx
xxxxxxxxxx
(セクション終了)
他の方のソースやいろいろなブログを見て勉強してきました。
方針は以下のとおりです。多分多くの人のやり方がこうでした。
- 10 * 10の土地で、「この一マスを埋め立てれば全体を一つの島にできる」一マスを探索する。
- 最初に選んだマスから深さ優先探索で、島のマス目数を数える。このとき探索したマス目数が、最初の入力で受け取った島のマス目 + (海を埋め立てていれば)1マスであれば、条件に合致。
【回答例】
import java.util.Scanner;
public class Main {
// 島の地図的なもの
static char[][] islandMap;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// 島の地図的なもの
islandMap = new char[10][10];
// 島のマスの数
int countIsland = 0;
// 最終的な出力
String ans = "NO";
// 入力を受け取って島の地図完成、島マスの個数カウント
for (int i = 0; i < 10; i++) {
islandMap[i] = sc.next().toCharArray();
for (int j = 0; j < 10; j++) {
if (islandMap[i][j] == 'o') {
countIsland++;
}
}
}
// 二重ループでマス目を左上のマスから探索
for (int i = 0; i < 10; i++) {
for (int j = 0; j < 10; j++) {
// 島数カウント一時変数
int countIslandInLoop = countIsland;
// 海の場合、陸地にする。また島の数を一つ増やす
if (islandMap[i][j] == 'x') {
islandMap[i][j] = 'o';
countIslandInLoop = countIsland + 1;
}
/*
* 深さ優先探索を行う。
* dfsCountIsland・・・dfsでカウントしている、陸続きの島の数
* checked・・・dfsによりマス目が探索済みかどうかの判定
*/
dfsIslandCount = 0;
boolean[][] checked = new boolean[10][10];
dfs(i, j, checked);
if (dfsIslandCount == countIslandInLoop) {
ans = "YES";
break;
}
// 埋め立てたマスを元に戻して次のループへ
if (countIslandInLoop == countIsland + 1) {
islandMap[i][j] = 'x';
}
}
if ("YES".equals(ans)) {
break;
}
}
System.out.println(ans);
}
// 現在dfsでカウントしている陸続きの島のマス目数
static int dfsIslandCount;
// 深さ優先探索
static void dfs(int i, int j, boolean[][] checked) {
// マス目を超えている・探索済み・海であるならば方向転換。
if (i < 0 || i > 9 || j < 0 || j > 9 || checked[i][j] || islandMap[i][j] == 'x') {
return;
}
// 今探索しているマスが陸地であれば陸地カウントをインクリメントする
if (islandMap[i][j] == 'o') {
dfsIslandCount++;
}
// 現在のマス目を探索済みにする
checked[i][j] = true;
// 上下左右のマスを探索する
dfs(i + 1, j, checked);
dfs(i - 1, j, checked);
dfs(i, j + 1, checked);
dfs(i, j - 1, checked);
return;
}
}
いやね、めっちゃ難しかった。グローバル変数に入れるところとか、探索の再帰のやり方とかめちゃ難しい。
あと関係ないんですけど、こういうアルゴリズムの例題ってAtCoderで用意してくれてるんですね。
AtCoder - atc001-a「深さ優先探索」
とりあえずこの問題のコードとしてはかけたので、dfsの部分を上から見ていきましょう。
2マス分くらい見れればいいかな。まず例の入力が次のとおりです。
xxxxxxxxxx
xoooooooxx
xxoooooxxx
xxxoooxxxx
xxxxoxxxxx
xxxxxxxxxx
xxxxoxxxxx
xxxoooxxxx
xxoooooxxx
xxxxxxxxxx
※×が海で、○が島。
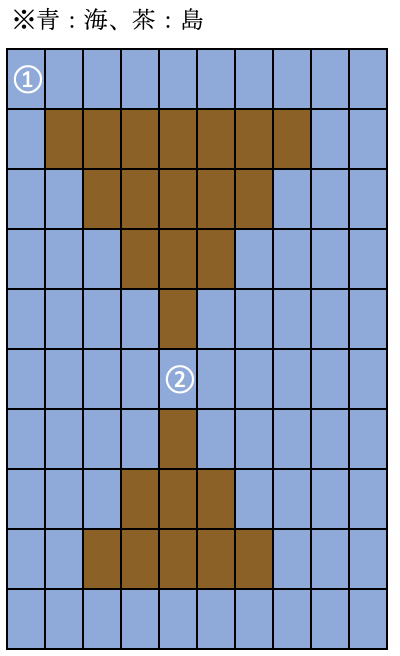
このときのmapは次のような感じです。
(まぁ、文字列からでもわかるけど。)
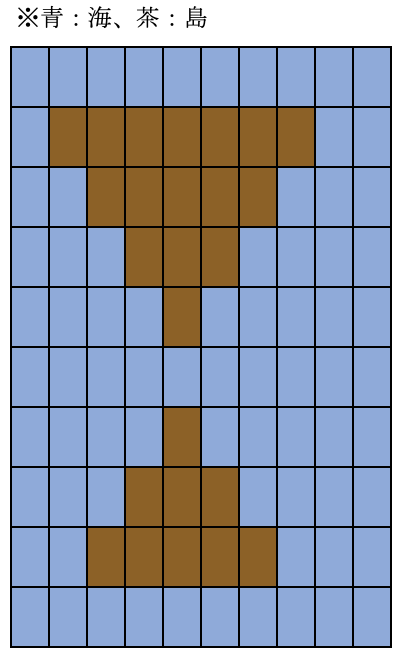
これの、①のマスについてのDFS、②のマスについてのDFSについて考えてみましょうか。
分かりやすさのために上記コードのdfsメソッド内、
1番の処理を「// マス目を超えている・探索済み・海であるならば方向転換。」のif文、
2番の処理を「// 今探索しているマスが陸地であれば陸地カウントをインクリメントする」の処理、
3番の処理を「// 現在のマス目を探索済みにする」の処理、
4番の処理を「// 上下左右のマスを探索する」の処理とします。(どれが呼び出されるかは都度説明します。)
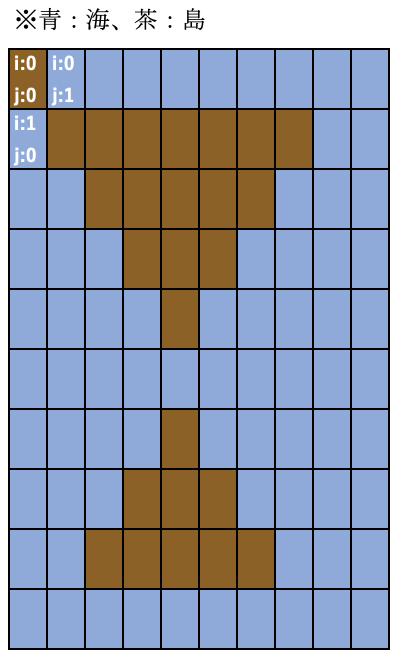
①の場合のDFS
ソースを追っていきましょう。
主にdfsでマスを移動するところについて重点的に解説します。
いちおうi,jの値も加えておきました。ではDFSです。現在いるマスを3番の処理で探索済みにしたあと、4番の処理に進みます。まず呼び出されるのは
dfs(i + 1, j, checked);
です。i=0,j=0なので
dfs(1, 0, checked);
ですね。
これでi=1,j=0のマスに移動しましたが、移動先は海なので1番の処理でif文に引っかかってしまいます。returnされます。
次は4番の処理の2行目に進みます。
dfs(i - 1, j, checked);
具体的に言うと
dfs(-1, 0, checked);
ですね。
i=-1,j=0のマス(地図外)に移動し、1番の処理でreturnされます。
3,4行目についても同様ですね。これで①のマスについては探索を終えるわけです。
まだ再帰っぽくなってないので分かりづらいですかね。ただまぁこういう分かりやすい例から考えるのもいいのではないかなぁと思います。
②の場合のDFS
では答えの例です。張り切ってDFSしましょう。
埋め立てをしてi,jの番号を書いた図がこちらです。
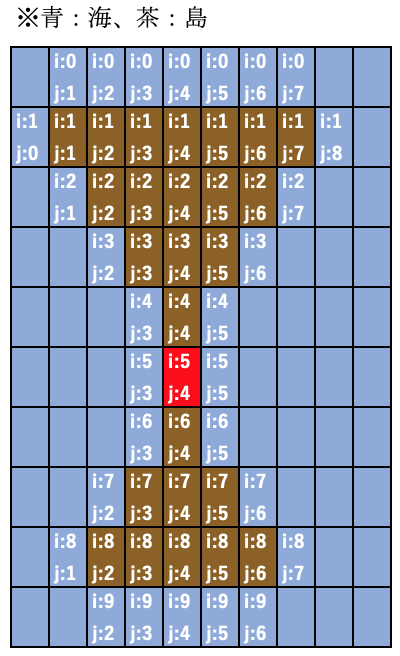
1回目の呼び出し、赤い部分について呼び出したあと、の動きをプログラムチックにインデントをつけて順番に書いていきます。インデントつくと再帰みたいな感じですね。
最初のdfs呼び出しの4番目の処理からいきます。はりきっていきましょう!!
現在(i,j) = (5,4)です。
再帰を含めて呼ばれる順番は以下のとおりです。
dfs(6, 4, checked);-
dfs(7, 4, checked); -
dfs(8, 4, checked); -
dfs(9, 4, checked);←海なので終わり -
dfs(7, 4, checked);←02行目で探索済みなので終わり -
dfs(8, 5, checked); -
dfs(9, 5, checked);←海なので終わり -
dfs(7, 5, checked); -
dfs(8, 5, checked);←06行目で探索済みのため終わり -
dfs(9, 5, checked);←海なので終わり -
dfs(7, 4, checked);←02行目で探索済みなので終わり -
dfs(7, 6, checked);←海なので終わり -
dfs(8, 6, checked); -
dfs(9, 6, checked);←海なので終わり -
dfs(7, 6, checked);←海なので終わり -
dfs(8, 7, checked);←海なので終わり -
dfs(8, 5, checked);←06行目で探索済みのため終わり -
dfs(8, 4, checked);←03行目で探索済みのため終わり -
dfs(8, 3, checked); -
dfs(9, 3, checked);←海なので終わり -
dfs(7, 3, checked); -
dfs(8, 3, checked);←19行目で探索済みのため終わり -
dfs(6, 3, checked);←海なので終わり -
dfs(7, 4, checked);←02行目で探索済みのため終わり -
dfs(7, 2, checked);←海なので終わり -
dfs(8, 2, checked); -
dfs(9, 2, checked);←海なので終わり -
dfs(7, 2, checked);←海なので終わり -
dfs(8, 3, checked);←19行目で探索済みのため終わり -
dfs(8, 1, checked);←海なので終わり -
dfs(8, 4, checked);←03行目で探索済みのため終わり -
dfs(6, 4, checked);←01行目で探索済みのため終わり -
dfs(7, 5, checked);←08行目で探索済みのため終わり -
dfs(7, 3, checked);←21行目で探索済みのため終わり -
dfs(5, 4, checked);←一番最初に探索済みのため終わり -
dfs(6, 5, checked);←海なので終わり -
dfs(6, 3, checked);←海なので終わり dfs(4, 4, checked);-
dfs(5, 4, checked);←一番最初に探索済みのため終わり -
dfs(3, 4, checked); -
dfs(4, 4, checked);←38行目で探索済みのため終わり -
dfs(2, 4, checked); -
dfs(3, 4, checked);←40行目で探索済みのため終わり -
dfs(1, 4, checked); -
dfs(2, 4, checked);←42行目で探索済みのため終わり -
dfs(0, 4, checked);←海なので終わり -
dfs(1, 5, checked); -
dfs(2, 5, checked); -
dfs(3, 5, checked); -
dfs(4, 5, checked);←海なので終わり -
dfs(2, 5, checked);←42行目で探索済みのため終わり -
dfs(3, 6, checked);←海なので終わり -
dfs(3, 4, checked);←40行目で探索済みのため終わり -
dfs(1, 5, checked);←42行目で探索済みのため終わり -
dfs(2, 6, checked); -
dfs(3, 6, checked);←海なので終わり -
dfs(1, 6, checked); -
dfs(2, 6, checked);←56行目で探索済みのため終わり -
dfs(0, 6, checked);←海なので終わり -
dfs(1, 7, checked); -
dfs(2, 7, checked);←海なので終わり -
dfs(0, 7, checked);←海なので終わり -
dfs(1, 8, checked);←海なので終わり -
dfs(1, 6, checked);←58行目で探索済みのため終わり -
dfs(1, 5, checked);←42行目で探索済みのため終わり -
dfs(2, 7, checked);←海なので終わり -
dfs(2, 5, checked);←42行目で探索済みのため終わり -
dfs(2, 4, checked);←38行目で探索済みのため終わり -
dfs(0, 5, checked);←海なので終わり -
dfs(1, 6, checked);←58行目で探索済みのため終わり -
dfs(1, 4, checked);←44行目で探索済みのため終わり -
dfs(1, 3, checked); -
dfs(2, 3, checked); -
dfs(3, 3, checked); -
dfs(4, 3, checked);←海なので終わり -
dfs(2, 3, checked);←74行目で探索済みのため終わり -
dfs(3, 4, checked);←38行目で探索済みのため終わり -
dfs(3, 2, checked);←海なので終わり -
dfs(1, 3, checked);←73行目で探索済みのため終わり -
dfs(2, 4, checked);←38行目で探索済みのため終わり -
dfs(2, 2, checked); -
dfs(3, 2, checked);←海なので終わり -
dfs(1, 2, checked); -
dfs(2, 2, checked);←82行目で探索済みのため終わり -
dfs(0, 2, checked);←海なので終わり -
dfs(1, 3, checked);←44行目で探索済みのため終わり -
dfs(1, 1, checked); -
dfs(2, 1, checked);←海なので終わり -
dfs(0, 1, checked);←海なので終わり -
dfs(1, 2, checked);←84行目で探索済みのため終わり -
dfs(1, 0, checked);←海なので終わり -
dfs(2, 3, checked);←74行目で探索済みのため終わり -
dfs(2, 1, checked);←海なので終わり -
dfs(0, 3, checked);←海なので終わり -
dfs(1, 4, checked);←44行目で探索済みのため終わり -
dfs(1, 2, checked);←84行目で探索済みのため終わり -
dfs(2, 5, checked);←42行目で探索済みのため終わり -
dfs(2, 3, checked);←74行目で探索済みのため終わり -
dfs(3, 5, checked);←50行目で探索済みのため終わり -
dfs(3, 3, checked);←75行目で探索済みのため終わり -
dfs(4, 5, checked);←海なので終わり -
dfs(4, 3, checked);←海なので終わり -
dfs(5, 5, checked);←海なので終わり -
dfs(5, 3, checked);←海なので終わり
お・・・終わったぁ・・・
超疲れました。人の手でやるもんじゃありませんでした。
まぁせっかくやったのでどんな動きで探索されていったのか確かめてみましょうね。
白文字で探索の順番を表してみました。
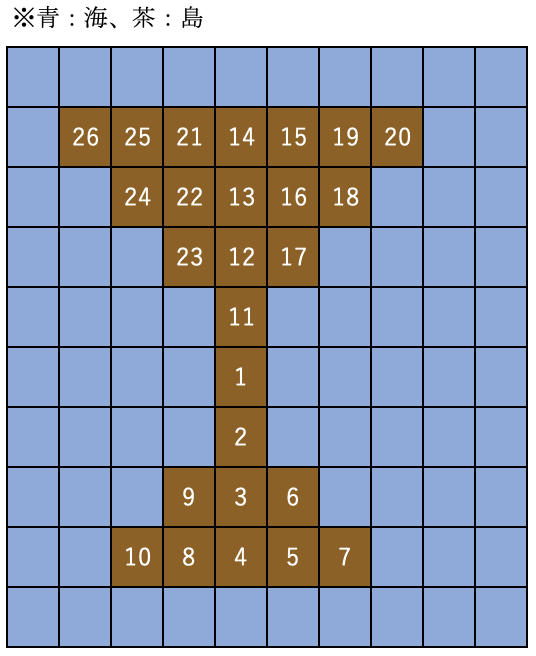
図を見てもらってもわかると思いますしloopの感じ見てもらってもわかると思いますが、DFSは「いけるとこまでいっていけなくなったら方向転換する」みたいな感じなのですね。
あと「スタック」って言葉が出てきたと思うんですけど、この再帰の方法、まさに先入後出しのスタックの順番になっているような感じがしますよね。スタックというデータ構造を使わずとも、再帰で実装書いたらスタックのような処理になることがよく分かりましたね。
深さ優先探索については理解できましたでしょうか?私はほんのり理解できました。(あぁ、疲れた・・・)
だいぶ長くなったので、幅優先探索についてはまた次回解説しようと思います。
次回もお楽しみに!!