金融データの特徴量エンジニアリング(初級編)

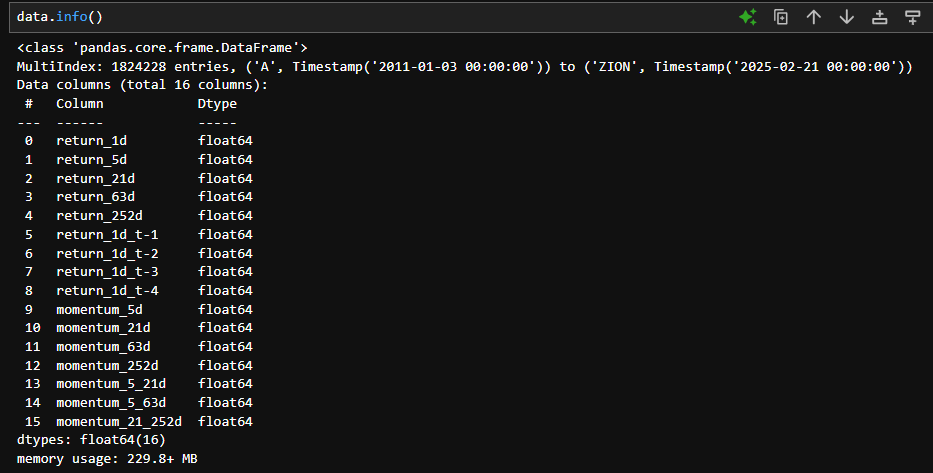
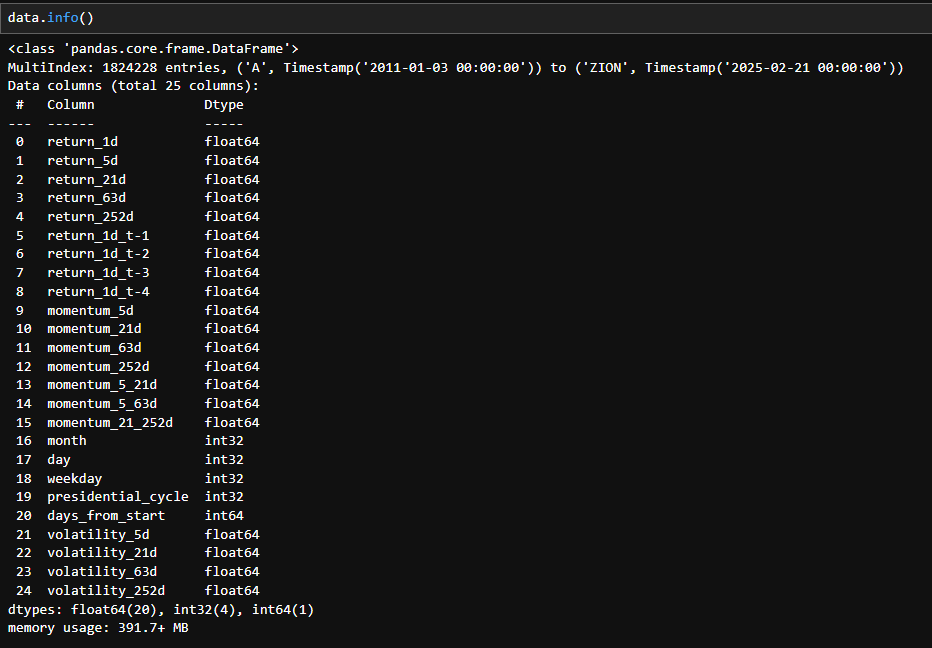
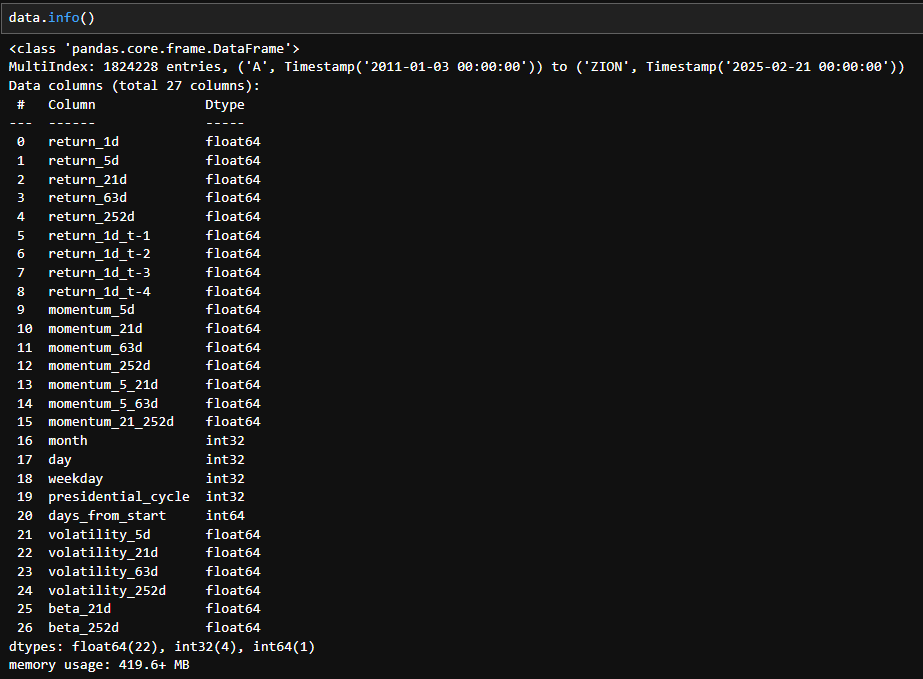
ここでは米国個別株の過去の市場データをもとにして、株価予測モデルのための特徴量エンジニアリングを行っていきます。

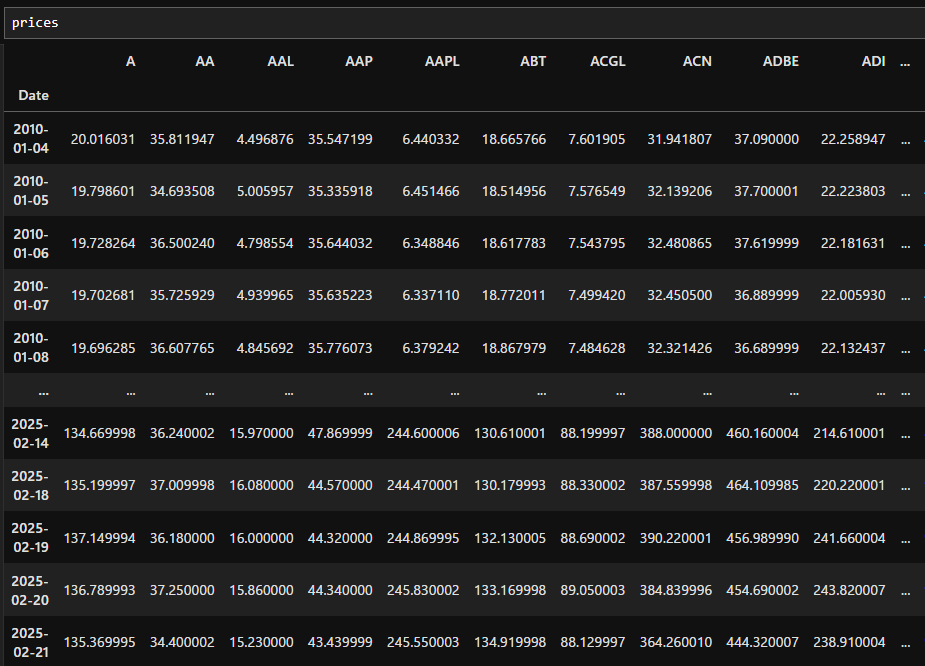
取り扱うデータ形式は、S&P500構成銘柄の「日付、四本値、出来高、配当、分割」です。

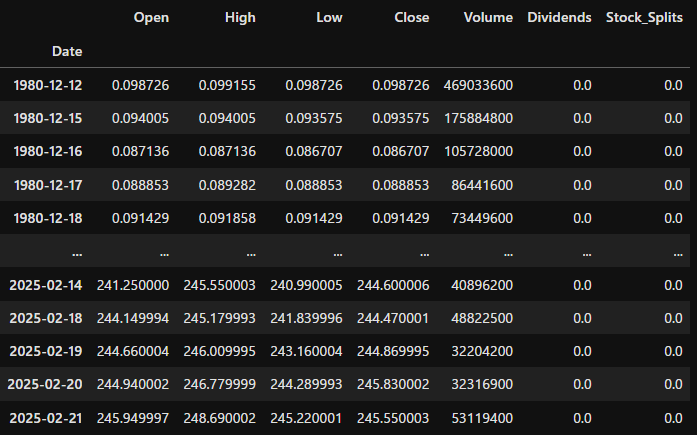
また、日ごとの配当と分割の調整済み終値を全銘柄分格納したデータフレームpricesをあらかじめ定義していることを想定します。

下記の書籍を参考にしています。
https://github.com/stefan-jansen/machine-learning-for-trading/tree/main/04_alpha_factor_research

過去リターン

lags = [1, 5, 21, 63, 252]としており、それぞれ「前日、一週間、一か月、三か月、一年」を意味します。

idx = pd.IndexSlice

# 外れ値カットの閾値
outlier_cutoff = 0.01
data = pd.DataFrame()
lags = [1, 5, 21, 63, 252]

for lag in lags:
    data[f'return_{lag}d'] = (
        prices
        .pct_change(lag)  # `lag` 日前からのリターン
        .stack()  # `(日付, ティッカー)` のロング形式に変換
        .pipe(lambda x: x.clip(lower=x.quantile(outlier_cutoff),
                               upper=x.quantile(1 - outlier_cutoff)))  # 外れ値をカット
        .add(1)
        .pow(1 / lag)  # 年率換算
        .sub(1)
    )
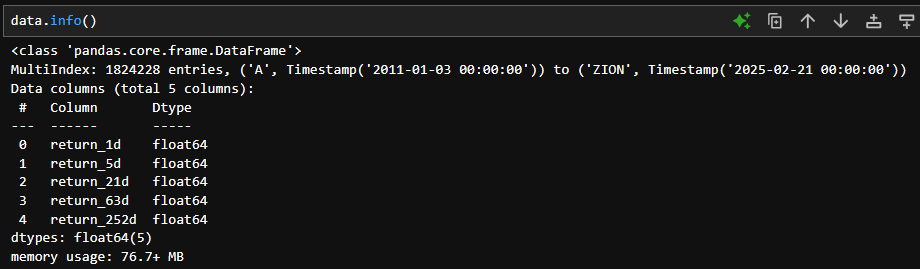
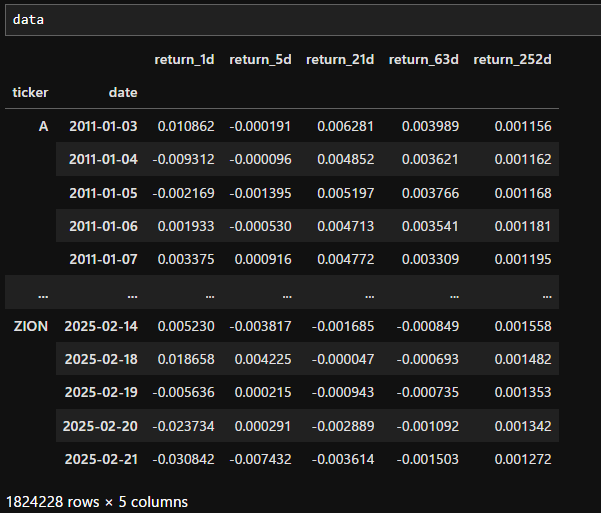
data = data.swaplevel().dropna() # インデックスを `(ティッカー, 日付)` の順に変更し、欠損値を削除

(ティッカー, 日付)をインデックスにして、5つの過去リターンを銘柄ごとに作成するコードとなっています。またリターンの極端な値を パーセンタイルベースのクリッピングclip()で処理しています。(例:1%以下は1%タイルの値に置換)

idx = pd.IndexSlice
data.index.names = ['ticker', 'date']

min_obs = 120
nobs = data.groupby(level='ticker').size()
keep = nobs[nobs>min_obs].index

data = data.loc[idx[keep,:], :]

このコードでデータ数が少ない銘柄を取り除くことが可能です。min_obs = 120としているのは、データ数が120未満の銘柄を削除するためです。

続けてt日前のデイリーリターンを追加します。

for t in range(1, 5):
    data[f'return_1d_t-{t}'] = data.groupby(level='ticker').return_1d.shift(t)

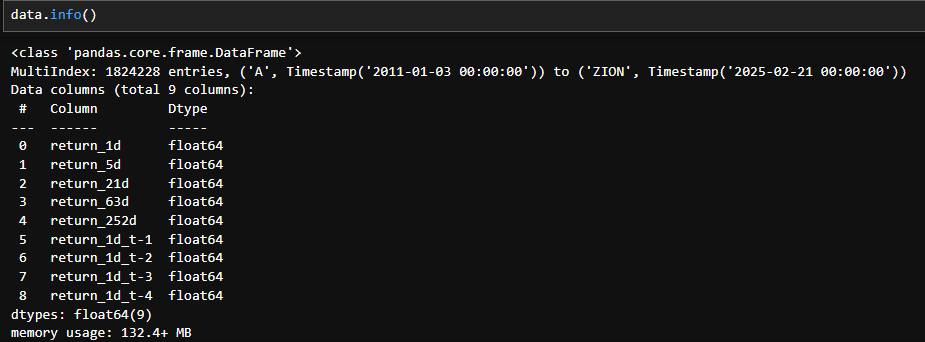
今回はrange(1, 5)とすることで過去一週間分のデイリーリターンを追加しました。

モメンタム

モメンタムの定義はStefan Jansen氏の書籍に記載されているコードを参照しています。

単純な過去リターンに対してモメンタムは、異なる期間のリターンの差を計算し、相対的な強さを測定する指標です。

# 各過去リターンとの差を計算
for lag in [5, 21, 63, 252]:  # 1日リターンは基準となるため除外
    data[f'momentum_{lag}d'] = data[f'return_{lag}d'].sub(data.return_1d)

data[f'momentum_5_21d'] = data[f'return_21d'].sub(data.return_5d)
data[f'momentum_5_63d'] = data[f'return_63d'].sub(data.return_5d)
data[f'momentum_21_252d'] = data[f'return_252d'].sub(data.return_21d)

カレンダー特徴量

株価リターン予測では季節性を考慮したい場合もあるかと思います。

# MultiIndex の 'date' レベルを取得
dates = data.index.get_level_values('date')

# 'month', 'day', 'weekday' のカラムを追加
data['month'] = dates.month  # 月 (1-12)
data['day'] = dates.day      # 日 (1-31)
data['weekday'] = dates.weekday  # 曜日 (0=月曜, 6=日曜)

このコードで月、日付、曜日を追加することができました。このようなカレンダー特徴量は、カテゴリー変数として扱うことが多いため、ワンホットエンコーディング等の処理が必要になることがあります。

書籍ではdates.yearをカテゴリー変数の特徴量として扱っていますが、運用時に新しい年になることも考慮するなら、あまり良い処理ではない気がします。そこで次のような特徴量を考えます。

# 西暦を4で割った余りを特徴量として追加
data['presidential_cycle'] = dates.year % 4

西暦を4年の周期で考え、西暦を4で割った余りを特徴量として追加します。余りが0の年は大統領選が行われる年なので株式市場にも何らかの影響があるかもしれません。
※大統領選は必ずしも「西暦を4で割った時の余りが0の年」に実施されるという決まりはないですが、例外はほとんどないため、自分の用途の範疇では問題ないと判断しました。

# 年始（1月1日）からの日数を計算
data['days_from_start'] = (dates - pd.to_datetime(dates.year.astype(str) + '-01-01')).days

次に年始からの日数を特徴量に追加してみます。この特徴量は量的変数を想定しています。

ボラティリティ

各銘柄のボラティリティを追加してみましょう。まずは関数としてボラティリティを定義します。

def volatility(returns, risk_free_rate=0.0, n=252):
    return np.std(returns, ddof=1) * np.sqrt(n)

ボラティリティの計算は株価リターンの標準偏差を年率換算することで求められます。pricesは日ごとの終値を入れたデータフレームですので、年率換算するときは、* np.sqrt(252)としています。

returns = prices.pct_change()
windows = [5, 21, 63, 252]

# 各ウィンドウサイズでボラティリティを計算し、データを統合
vol_dfs = []
for window in windows:
    vol = returns.rolling(window=window).apply(volatility, raw=True)
    vol = vol.stack().rename(f"volatility_{window}d").swaplevel().sort_index()
    vol.index.names = ['ticker', 'date']
    vol_dfs.append(vol)

# 全てのボラティリティデータを統合
vol_all = pd.concat(vol_dfs, axis=1)

# `data` にマージ
data = data.join(vol_all, how="left")

このような処理でdataにボラティリティを追加することができます。同様の操作で関数の定義を変えれば任意の計算式で特徴量を作成することができます。

ベータ

pricesにはS&P500の構成銘柄が入っています。各銘柄のベータを特徴量に追加してみましょう。

まずはベータの計算に必要なベンチマークを取得しましょう。

import yfinance as yf

# SPY（S&P 500 ETF）のデータを取得（終了日を1日後に設定）
spy = yf.download('SPY', start=prices.index.min(), end=prices.index.max() + pd.Timedelta(days=1))
benchmark = spy.loc[:, ('Close', 'SPY')]
benchmark = benchmark.to_frame()
benchmark = benchmark.droplevel(level=0, axis=1)

今回はyfinanceで取得したSPYをベンチマークとします。

def beta(returns, benchmark):
    """与えられた銘柄のリターンとベンチマークのリターンを使ってベータを計算"""
    if len(returns) < 2 or len(benchmark) < 2:
        return np.nan  # データ不足時は NaN を返す

    matrix = np.cov(returns, benchmark)
    return matrix[0, 1] / matrix[1, 1]  # 共分散行列からベータを計算

ベータは共分散をベンチマーク分散で割って求める場合はこのように書けます。

returns = prices.pct_change().dropna()
benchmark_returns = benchmark['SPY'].pct_change().dropna()
windows = [21, 252]

# 各ウィンドウのベータを格納するリスト
beta_dfs = []

for window in tqdm(windows, desc="Calculating Beta Features"):
    beta_values = (
        returns.rolling(window)
        .apply(lambda x: beta(x, benchmark_returns.loc[x.index]), raw=False)
    )

    # インデックスを (ティッカー, 日付) の順に整理
    beta_values = beta_values.stack().rename(f"beta_{window}d").swaplevel().sort_index()
    beta_values.index.names = ['ticker', 'date']

    # 計算したデータをリストに追加
    beta_dfs.append(beta_values)

# すべてのウィンドウのベータを統合
beta_all = pd.concat(beta_dfs, axis=1)

# `data` にマージ
data = data.join(beta_all, how="left")

作成したデータの保存

with pd.HDFStore('feature_dataset.h5', mode='w') as store:
    store.put('data', data, format='table')
    store.close()

print("Feature dataset saved to 'feature_dataset.h5'")

上記コードでHDF5に保存することが可能です。

呼び出すときは

with pd.HDFStore('feature_dataset.h5', mode='r') as store:
    dataset = store['data']

これでOKです。