LightGBMを使ってみよう

この記事では毛利拓也著「LightGBM予測モデル実装ハンドブック」(秀和システム)を参考にLightGBMを動作させてみます。

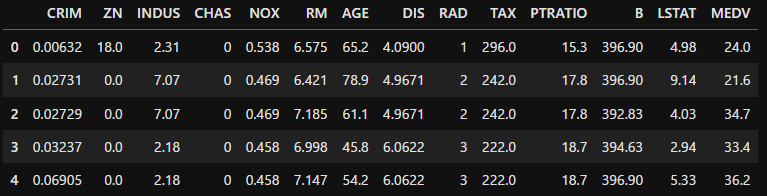
まずは練習用のデータセットを読み込みます。ここで扱うのは住宅価格情報を記録したデータです。MEDVという列は住宅価格を示すデータとなっており、その他の列は部屋数、幹線道路へのアクセス指数、地域の犯罪発生数など住宅価格を左右させそうな変数が複数入っています。

import pandas as pd
df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/housing/housing.data', header=None, sep='\s+')
df.columns=['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
df.head()

データはカリフォルニア大学アーバイン校(UCI)が無償提供しているものです。以下サイトより多種の練習用データが入手可能です。

EDA(探索的データ解析)

取得したデータの中からMEDVを教師データにする想定でEDAを実施します。

まずは欠損値をチェックしていきます。今回はmissingnoを使ってみます。

import missingno as msno
msno.matrix(df)
df.isnull().sum()

欠損値はないみたいなのでそのまま続けます。

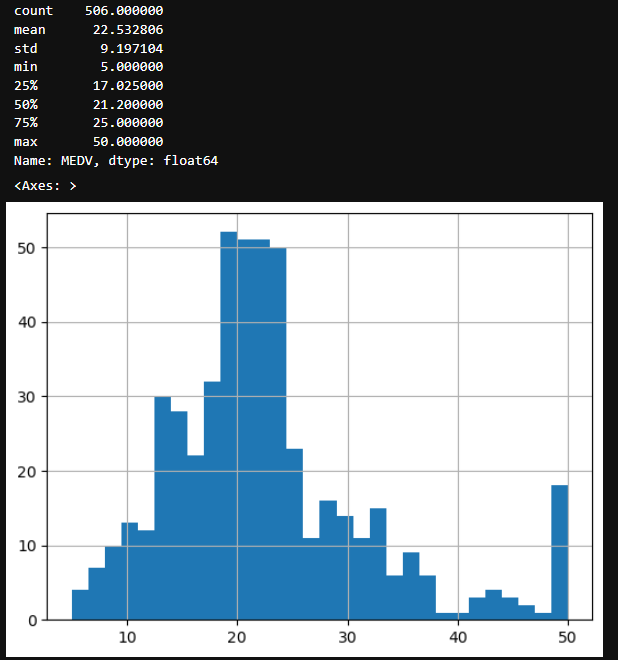
次は教師データMEDVについて確認していきましょう。下記のコードで基本的な統計情報とヒストグラムを表示します。

print(df['MEDV'].describe())
df['MEDV'].hist(bins=30)

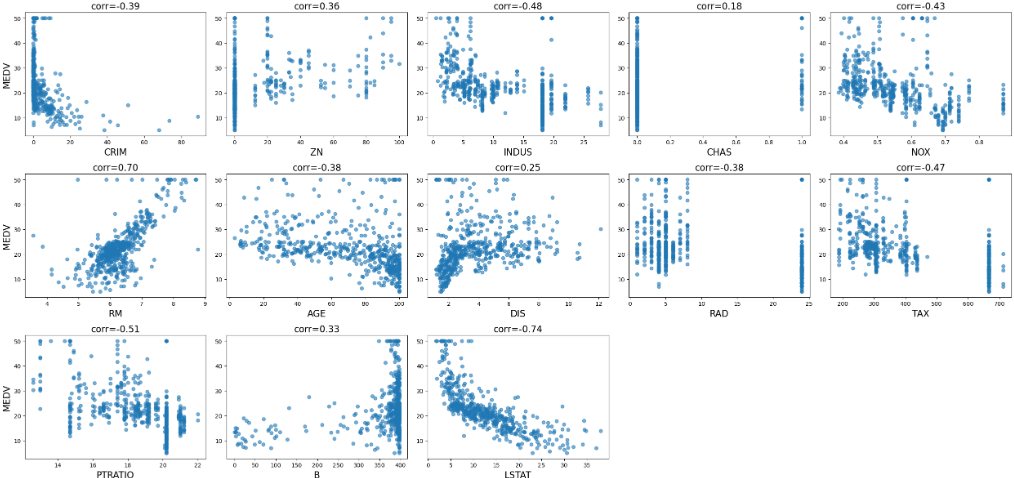
ではこの教師データと他の特徴量との関係性を散布図で表示していきましょう。

import matplotlib.pyplot as plt

features = df.columns[:-1]
n_features = len(features)

n_rows, n_cols = 3, 5
fig, axes = plt.subplots(n_rows, n_cols, figsize=(5 * n_cols, 4 * n_rows))
axes = axes.flatten()

for i, feature in enumerate(features):
    ax = axes[i]
    ax.scatter(df[feature], df['MEDV'], alpha=0.6)
    ax.set_xlabel(feature, fontsize=16)
    
    if i % n_cols == 0:
        ax.set_ylabel("MEDV", fontsize=16)
    
    corr = df[feature].corr(df['MEDV'])
    ax.set_title(f'corr={corr:.2f}', fontsize=16)

for j in range(len(features), n_rows * n_cols):
    fig.delaxes(axes[j])

plt.tight_layout()
plt.show()

ぱっと見たところでは、RM(部屋数)やLSTAT(低所得者の割合)が住宅価格に大きく影響しているみたいですね。

LightGBMによる住宅価格予測

では、さっそくLightGBMを使って予測を行っていきましょう。

先ほどのデータセットからMEDVを除いて特徴量行列Xを作成し、MEDVをターゲット配列yとします。

# 特徴量と目的変数の設定
X = df.drop(['MEDV'], axis=1)
y = df['MEDV']

Xとyをそれぞれテストデータ_testと訓練データ_trainに分けます。

from sklearn.model_selection import train_test_split

# 学習データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, shuffle=True, random_state=0)

訓練データのみを使ってモデルを学習します。このときにLightGBMのハイパーパラメーターを指定する必要があります。

import lightgbm as lgb

lgb_train = lgb.Dataset(X_train, y_train)

params = {'objective': 'mse',
          'num_leaves': 5,
          'seed': 0,
          'verbose': -1,
}

# モデルの学習
model = lgb.train(params,
                  lgb_train,
                  num_boost_round=50,
                  valid_sets=[lgb_train],
                  valid_names=['train'],
                  callbacks=[lgb.log_evaluation(10)])

評価

学習が終わったら予測結果を確認しましょう。

import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error

# 予測
y_train_pred = model.predict(X_train) 
y_test_pred = model.predict(X_test)

# RMSE
rmse_train = mean_squared_error(y_train, y_train_pred) ** 0.5
rmse_test = mean_squared_error(y_test, y_test_pred) ** 0.5

fig, axes = plt.subplots(1, 2, figsize=(12, 5))

# 学習データ
axes[0].scatter(y_train_pred, y_train, alpha=0.6)
axes[0].plot([y_train_pred.min(), y_train_pred.max()],
             [y_train_pred.min(), y_train_pred.max()], 'r--')
axes[0].set_xlabel('Predicted MEDV')
axes[0].set_ylabel('Actual MEDV')
axes[0].set_title(f'Train RMSE: {rmse_train:.2f}')

# テストデータ
axes[1].scatter(y_test_pred, y_test, alpha=0.6)
axes[1].plot([y_test_pred.min(), y_test_pred.max()],
             [y_test_pred.min(), y_test_pred.max()], 'r--')
axes[1].set_xlabel('Predicted MEDV')
axes[1].set_ylabel('Actual MEDV')
axes[1].set_title(f'Test RMSE: {rmse_test:.2f}')

plt.tight_layout()
plt.show()

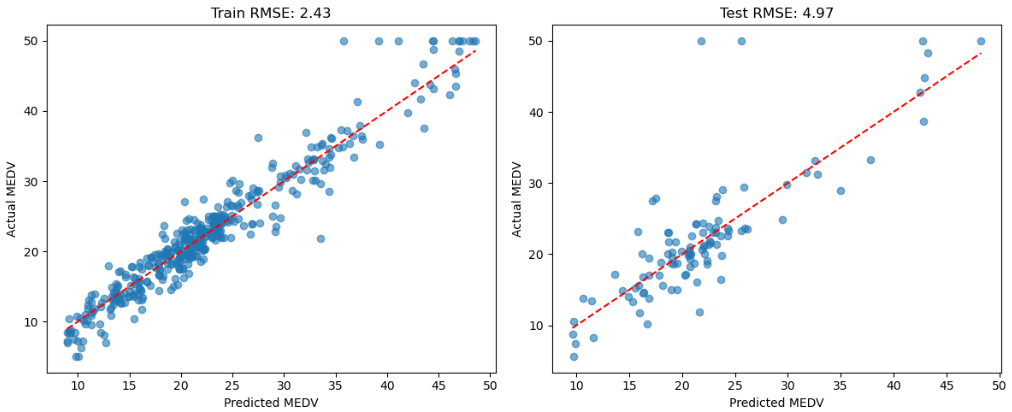
正解データをy軸に、予測値をx軸にした散布図を表示しました。左が訓練データ、右がテストデータです。赤線に近いほど予測がうまく行っており、遠いほど誤差が大きいことを示しています。各RMSEを計算しており、この数値は予測誤差の大きさに応じて決まる評価指標です。

特徴量重要度

学習を終えたモデルから、どの特徴量が重要だったかを調べます。

import numpy as np
# 特徴量の重要度の可視化
importances = model.feature_importance(importance_type='gain') # 特徴量の重要度
indices = np.argsort(importances)[::-1] # 特徴量の重要度を降順にソート

plt.figure(figsize=(8, 4)) #プロットのサイズ指定
plt.title('Feature Importance') # プロットのタイトルを作成
plt.bar(range(len(indices)), importances[indices]) # 棒グラフを追加
plt.xticks(range(len(indices)), X.columns[indices], rotation=90) # X軸に特徴量の名前を追加
plt.show() # プロットを表示

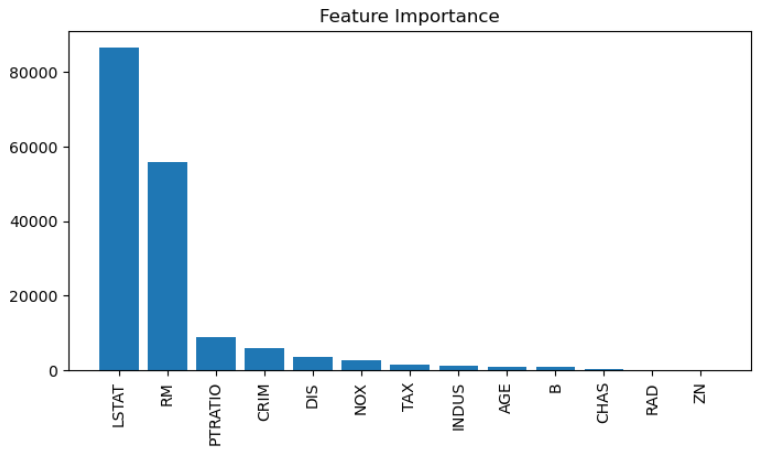
LSTATとRMが重要だったことはグラフから読み取れます。この結果はEDAで視覚的に確認した認識と一致しているので、うまくデータの傾向を学習できていそうな気がしますね。

plot_treeを使えば学習済みモデルの木を可視化することができます。

# 1本目の木の可視化
lgb.plot_tree(model, tree_index=0, figsize=(10, 10))

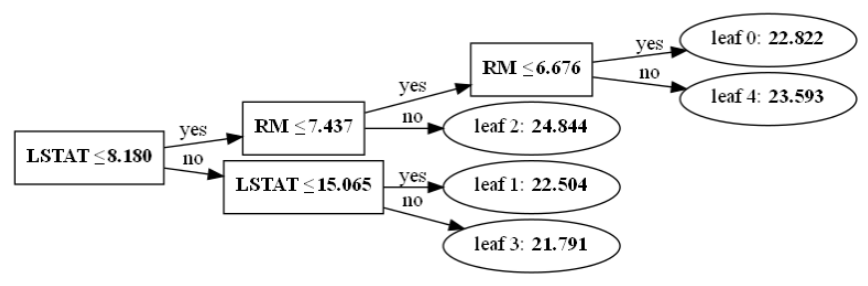
今回のブースティング回数は50回(num_boost_round=50)なので、tree_indexは0から49を指定できます。

Optunaを用いたハイパーパラメータチューニング

先ほどはLightGBMのハイパーパラメータを書籍の数値をそのまま使いましたが、実際にはハイパーパラメータをどんな数値にすればいいのかわからないことがほとんどです。そこで適切なハイパーパラメータを探索するためにOptunaを利用してみましょう。

ハイパーパラメータチューニング用に学習データをさらに分割します。

# 学習データの一部を検証データに分割
X_tr, X_va, y_tr, y_va = train_test_split(X_train, y_train, test_size=0.2, shuffle=True, random_state=1)
print('X_trの形状：', X_tr.shape, ' y_trの形状：', y_tr.shape, ' X_vaの形状：', X_va.shape, ' y_vaの形状：', y_va.shape)

次に探索するハイパーパラメータの選択と探索範囲を指定します。

# 固定値のハイパーパラメータ
params_base = {
    'objective': 'mse',
    'random_seed': 1234,
    'learning_rate': 0.02,
    'min_data_in_bin': 3,
    'bagging_freq': 1,
    'bagging_seed': 0,
    'verbose': -1,
}

# ハイパーパラメータ最適化

# ハイパーパラメータの探索範囲
def objective(trial):
  params_tuning = {
      'num_leaves': trial.suggest_int('num_leaves', 5, 200),
      'min_data_in_leaf': trial.suggest_int('min_data_in_leaf', 2, 30),
      'max_bin': trial.suggest_int('max_bin', 200, 400),
      'bagging_fraction': trial.suggest_float('bagging_fraction', 0.1, 1),
      'feature_fraction': trial.suggest_float('feature_fraction', 0.1, 1),
      'min_gain_to_split': trial.suggest_float('min_gain_to_split', 0.01, 1, log=True),
      'lambda_l1': trial.suggest_float('lambda_l1', 0.01, 1, log=True),
      'lambda_l2': trial.suggest_float('lambda_l2', 0.01, 1, log=True),
  }
  
  # 探索用ハイパーパラメータの設定
  params_tuning.update(params_base)

  lgb_train = lgb.Dataset(X_tr, y_tr)
  lgb_eval = lgb.Dataset(X_va, y_va)
  
  # 探索用ハイパーパラメータで学習
  model = lgb.train(params_tuning,
                    lgb_train,
                    num_boost_round=50,
                    valid_sets=[lgb_train, lgb_eval],
                    valid_names=['train', 'valid'],
                    callbacks=[lgb.early_stopping(100),
                               lgb.log_evaluation(500)])
  
  y_va_pred = model.predict(X_va, num_iteration=model.best_iteration)
  score =  mean_squared_error(y_va, y_va_pred)
  print('')

  return score

ここまで設定し終えたら、ハイパーパラメータ最適化を実行します。このデータと設定ではそれほど時間はかかりませんが、扱うデータによっては実行にけっこう時間がかかったりします。実行するとログが大量に流れますが正常です。

import optuna
study = optuna.create_study(sampler=optuna.samplers.TPESampler(seed=0), direction='minimize')
study.optimize(objective, n_trials=100)

最適化が終わったら結果を見てみましょう。

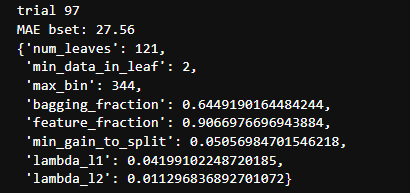
# 最適化の結果確認
trial = study.best_trial
print(f'trial {trial.number}')
print('MAE bset: %.2f'% trial.value)
display(trial.params)

このパラメータで学習すればいいわけです。

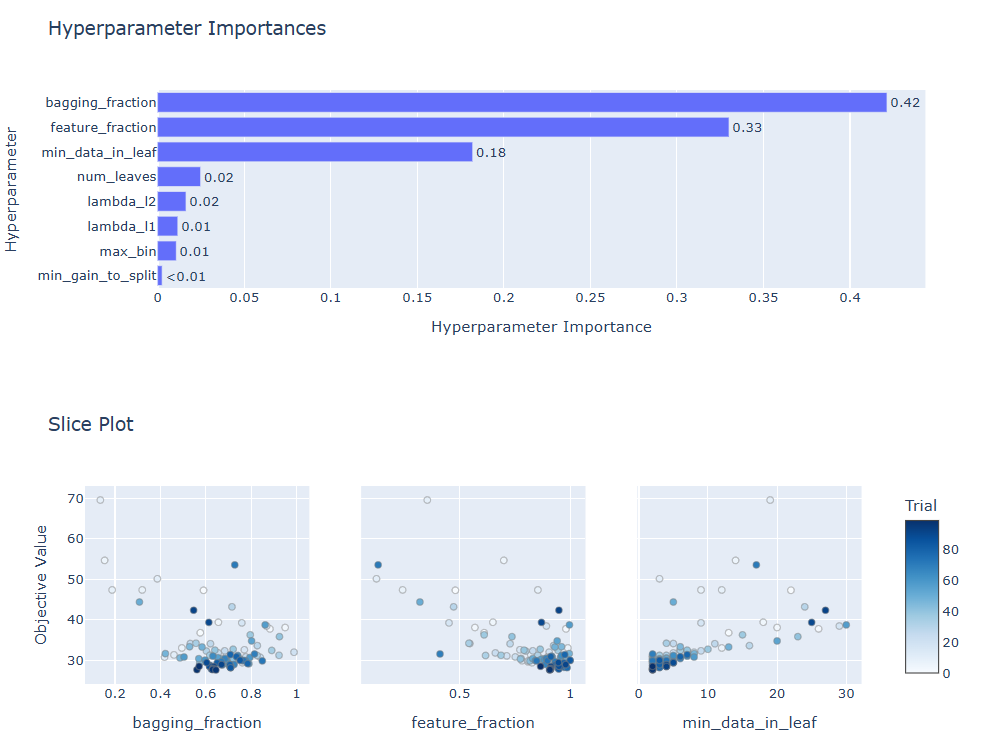
またoptuna.visualizationで最適化結果の詳細を確認することができます。

optuna.visualization.plot_param_importances(study).show()
optuna.visualization.plot_slice(study, params=['min_data_in_leaf', 'feature_fraction', 'bagging_fraction']).show()

では最適化結果を使ってモデルを再学習させてみましょう。

# 最適化されたパラメータで再学習
params_best = study.best_trial.params.copy()
params_best.update({
    'objective': 'mse',
    'seed': 0,
    'verbose': -1
})

lgb_train_best = lgb.Dataset(X_train, y_train)
model_best = lgb.train(
    params_best,
    lgb_train_best,
    num_boost_round=50,
    valid_sets=[lgb_train_best],
    valid_names=['train'],
    callbacks=[lgb.log_evaluation(10)]
)

# 予測
y_test_pred_best = model_best.predict(X_test)

# RMSE
rmse_test_best = mean_squared_error(y_test, y_test_pred_best) ** 0.5

fig, axes = plt.subplots(1, 3, figsize=(18, 5))
# 1. 学習データ（初期パラメータ）
axes[0].scatter(y_train_pred, y_train, alpha=0.6)
axes[0].plot([y_train_pred.min(), y_train_pred.max()],
             [y_train_pred.min(), y_train_pred.max()], 'r--')
axes[0].set_xlabel('Predicted MEDV')
axes[0].set_ylabel('Actual MEDV')
axes[0].set_title(f'Train (initial)\nRMSE: {rmse_train:.2f}')

# 2. テストデータ（初期パラメータ）
axes[1].scatter(y_test_pred, y_test, alpha=0.6)
axes[1].plot([y_test_pred.min(), y_test_pred.max()],
             [y_test_pred.min(), y_test_pred.max()], 'r--')
axes[1].set_xlabel('Predicted MEDV')
axes[1].set_ylabel('Actual MEDV')
axes[1].set_title(f'Test (initial)\nRMSE: {rmse_test:.2f}')

# 3. テストデータ（最適化パラメータ）
axes[2].scatter(y_test_pred_best, y_test, alpha=0.6, c='green')
axes[2].plot([y_test_pred_best.min(), y_test_pred_best.max()],
             [y_test_pred_best.min(), y_test_pred_best.max()], 'r--')
axes[2].set_xlabel('Predicted MEDV')
axes[2].set_ylabel('Actual MEDV')
axes[2].set_title(f'Test (tuned)\nRMSE: {rmse_test_best:.2f}')

plt.tight_layout()
plt.show()

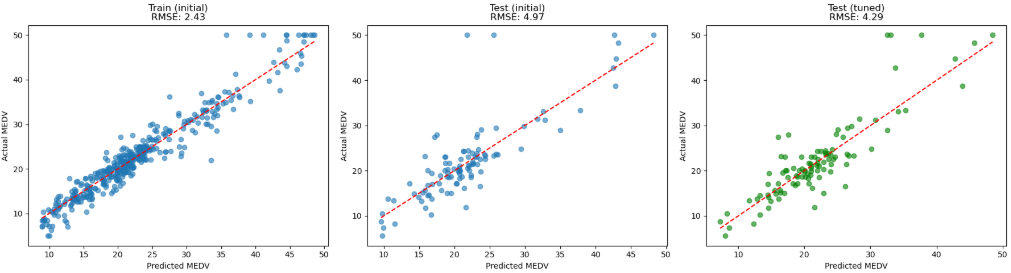
ハイパーパラメータ最適化後のテスト結果を一番右(緑の散布図)に追加しましたが、少しだけ改善したようです。場合によっては劇的に改善するケースもあるのですが、書籍に記載されていた元のパラメータがある程度調整されていたのかもしれないですね。