計算負荷の偏り
C/C++プログラミングで,OpenMPのお世話になっています。頭が上がりません ![]()
画像処理をはじめ,配列を扱うプログラムでは,配列の各要素を並列計算することがよくありますよね。
例えば,2次元画像の場合,こんな感じです。
// 画像サイズ
int img_shape[2] = { 512, 512 };
// 画素数
int num_pixel = img_shape[0] * img_shape[1];
// 2次元画像
std::vector<float> img( num_pixel );
// バイナリファイルを読み込む(架空の関数です)
read_from_file( "image.f256x256.bin", img );
// 画素毎の並列処理
#pragma omp parallel for
for ( int n = 0; n < num_pixel; n++ ) {
// 多次元インデックス
int index[2] = { n%img_shape[0], n / img_shape[0] };
// 各画素の処理
// ...
}
ここで,値が正の画素のみを処理対象とする場合を考えます。
並列計算の部分はこんな感じになります。
#pragma omp parallel for
for ( int n = 0; n < num_pixel; n++ ) {
// 多次元インデックス
int index[2] = { n % img_shape[0], n / img_shape[0] };
// 各画素の処理
if ( img[n] > 0.f )
{
// ...
}
}
この何気ない実装には,実はとても大きな問題があります。
それは,処理対象の画素が一部の領域に偏っている場合に,並列計算の効率が落ちることです。
例えば,下図のように偏っている場合に,並列スレッド数を4にすると,スレッド0,1,2,3のうち,スレッド1とスレッド2だけに負荷が集中し,スレッド0とスレッド3は開店休業状態になり,演算能力を持て余してしまいます ![]()

この記事では 「スレッド負荷を分散して本来の演算能力を引き出す方法」 を紹介します。
対処方法1
一番ナイーブな対処方法は,画素番号のシーケンシャルな配列index_map={0,1,2,...,num_pixel-1}
をシャッフルして,画素番号のマッピング(読み替え) を行うことです。
#pragma omp parallel for
for ( int k = 0; k < num_pixel; k++ ) {
// マッピング
int n = index_map[k];
// 多次元インデックス
int index[2] = { n % img_shape[0], n / img_shape[0] };
// 各画素の処理
if ( img[n] > 0.f )
{
// ...
}
}
これで計算負荷は分散できますが,この実装には,別の大きな問題があります。
それは,画素数と同じサイズのマッピング配列が必要であること,つまり,Memory-Efficient でないことです。
例えば,非破壊検査CTでは,2048 * 2048 * 2048といった巨大な3次元画像を扱う場合があり,その場合,マッピング配列(8バイト要素)のサイズは,なんと約70GBになります。流石にキツイ。
ということで,この対処方法は,巨大な画像を扱う場合,実用的ではありません。
対処方法2
シンプルでMemory-Efficientな対処方法があります。
軸毎にシャッフルされたマッピング配列を準備すればいいのです。
例えば,2次元画像であれば,横方向・縦方向のそれぞれで,マッピング配列index_map_x, index_map_yを準備すれば済むのです。
この方法では,マッピング配列のサイズは,各軸のサイズになります。2048 * 2048 * 2048の3次元画像であっても,たったの24KBです。余裕!
#pragma omp parallel for
for ( int k = 0; k < num_pixel; k++ ) {
// 多次元インデックス
int index[2] = { k % img_shape[0], k / img_shape[0] };
// マッピング
index[0] = index_map_x[index[0]];
index[1] = index_map_y[index[1]];
// 線形インデックス
int n = index[0] + index[1] * img_shape[0];
// 各画素の処理
if ( img[n] > 0.f )
{
// ...
}
}
この方法でも負荷分散でき,Memory-Efficientなので実用的でもあります。
この方法をふと思い付きましたが,極めてフツーな考え方なので,既に誰かがやってるはずです。
対処方法3
わざわざインデックスのマッピング配列を準備しなくても,マッピング関数を準備すれば,それで済みます。
例えば,配列サイズが15,並列スレッド数が4の場合は,このような「等間隔」なマッピングが考えられます。
{0,1,2,3,4,5,6,7,8,9,10,11,12,13,14} --> {0,4,8,12,1,5,9,13,2,6,10,14,3,7,11}
つまり,f(0)=0, f(1)=4, ..., f(14)=11 を満たすマッピング関数f(・)が必要です。
以下は,(恐らく)任意の配列サイズNと任意の並列スレッド数Tに対応したマッピング関数です。
// マッピング関数
int equipitched_map( int index, int N, int T )
{
return
( N > T )
? ( ( index * T ) - ( ( index * T ) / N ) * ( N - ( N % T == 0 ) ) )
: index;
}
このマッピング関数を使うと,次のような実装に帰着します。
線形インデックスをマッピングする場合(対処方法1の改良版)
#pragma omp parallel for
for ( int k = 0; k < num_pixel; k++ ) {
// マッピング
int n = equipitched_map( k, num_pixel, omp_get_max_threads() );
// 多次元インデックス
int index[2] = { n % img_shape[0], n / img_shape[0] };
// 各画素の処理
if ( img[n] > 0.f )
{
// ...
}
}
多次元インデックスをマッピングする場合(対処方法2の改良版)
#pragma omp parallel for
for ( int k = 0; k < num_pixel; k++ ) {
// 多次元インデックス
int index[2] = { k % img_shape[0], k / img_shape[0] };
// マッピング
index[0] = equipitched_map( index[0], img_shape[0], omp_get_max_threads() );
index[1] = equipitched_map( index[1], img_shape[1], omp_get_max_threads() );
// 線形インデックス
int n = index[0] + index[1] * img_shape[0];
// 各画素の処理
if ( img[n] > 0.f )
{
// ...
}
}
最後に
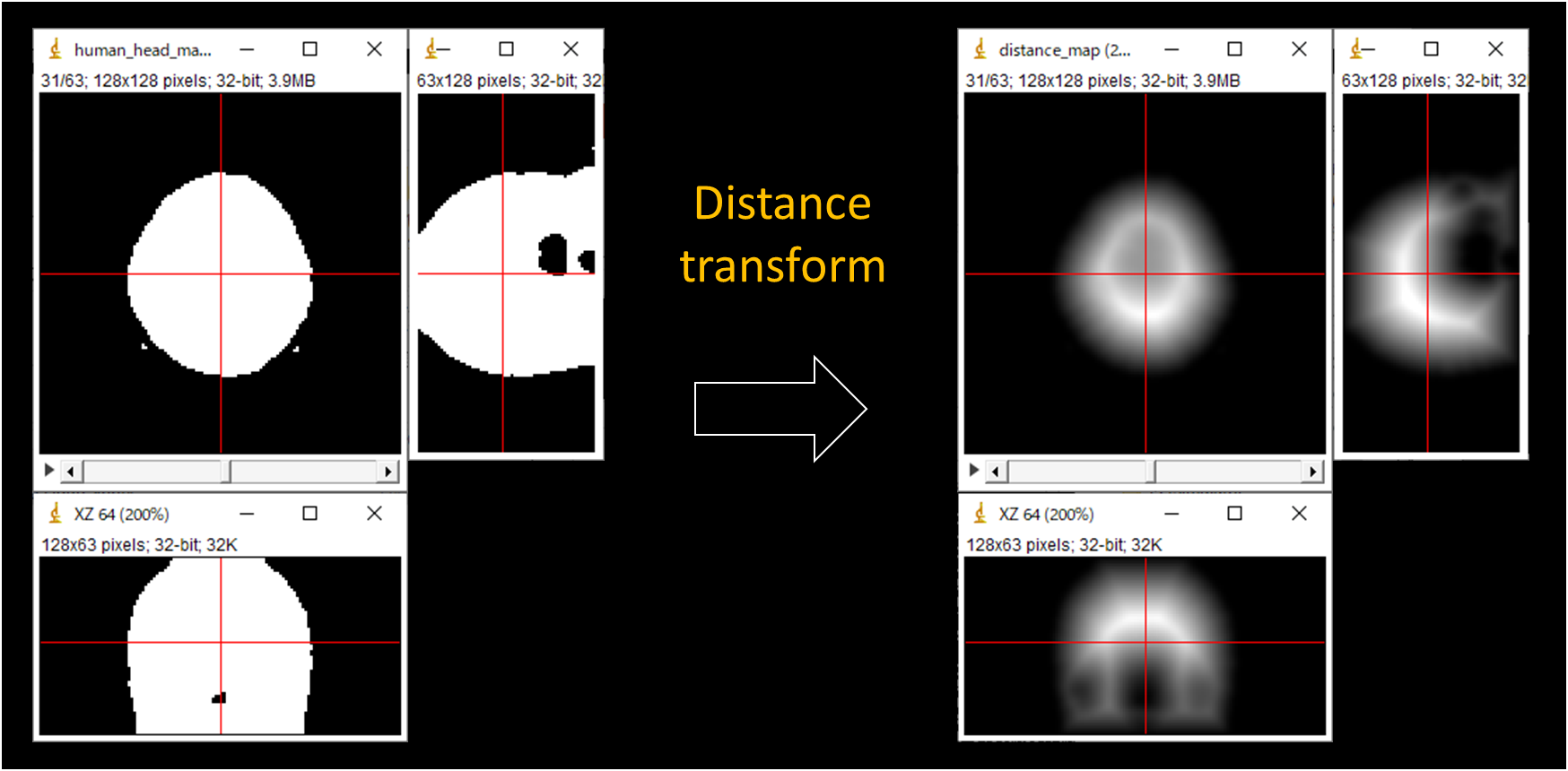
なぜこんなことを考えるに至ったかというと,MySimuに3次元画像を距離変換するプログラムを実装していて,「なんか計算遅いな」となって,「前景の画素しか処理対象にならないからか?」と思って調べてみた,というような感じです。
下図が実例(画像サイズ:128x128x63)で,インデックスのマッピングを実装したら,計算時間は20秒から半減しました ![]()
以上です