最適化問題の理論をチートシートレベルでまとめてみました。過去にシリーズでやってたやつをまとめたやつです。
自分用に作っているので、第三者的に分かりづらい可能性がある点、厳密性に欠く部分がある可能性がある点は悪しからず。
1. 最適化問題の分類
以下のように分類される。
2. 非線形計画
凸とも限らない・線形とも限らない一般的な連続最適化問題を扱う理論と解法。
\begin{array}[lll]
&\min &f(\boldsymbol{x}) \\
s.t. &g_i(\boldsymbol{x}) \leq 0, &i=1,\cdots,m, \\
&h_l(\boldsymbol{x})=0, &l=1,\cdots,r
\end{array} \tag{2-1} \label{2.1}
2.1.無制約非線形計画
制約条件がない場合。
\min f(\boldsymbol{x}) \tag{2-2} \label{2.2}
2.1.1. 最適性条件
2.1.1.1. 1次の最適性条件
\nabla f(\boldsymbol{x})=\boldsymbol{0} \tag{2-3}
2.1.1.2. 2次の最適性必要条件
\nabla f(\boldsymbol{x})=\boldsymbol{0} \land \nabla^2 f(\boldsymbol{x}) \succeq O \tag{2-4}
2.1.1.3. 2次の最適性必要条件
\nabla f(\boldsymbol{x})=\boldsymbol{0} \land \nabla^2 f(\boldsymbol{x}) \succ O \tag{2-5}
2.1.2. 解法
2.1.2.1. 最急降下法
現在の点$\boldsymbol{x}$を以下の更新公式にしたがって点$\boldsymbol{x}_{k+1}$に更新する。
\begin{array}
~\boldsymbol{x}_{k+1}=\boldsymbol{x}_k +\alpha_k \boldsymbol{d}_k \\
\boldsymbol{d}_k = -\nabla f(\boldsymbol{x}_k)
\end{array} \tag{2-6}
ステップ幅$\alpha_k$は、直線探索 ($l_k(\alpha)=f(\boldsymbol{x}_k+\alpha\boldsymbol{d}_k)$を最小化する$\alpha$を求める) によって決定する。ただし厳密な最適解を求めることは難しいため、Armijoの条件やWolfeの条件といったより弱い条件が用いられる。直線探索の実装にはバックトラック法がよく用いられる。バックトラック法とは、まず大きめに$\alpha$を選び、徐々に$\alpha$を小さくして条件が最初に満たされるところをステップ幅$\alpha_k$とする方法である。
大域的収束性が保証される (大域的最適解への収束が保証されているわけではないため注意)。
2.1.2.2. Netwon法
現在の点$\boldsymbol{x}$を以下の更新公式にしたがって点$\boldsymbol{x}_{k+1}$に更新する。
\begin{array}
~\boldsymbol{x}_{k+1}=\boldsymbol{x}_k +\alpha_k \boldsymbol{d}_k \\
\nabla^2 f(\boldsymbol{x}_k)\boldsymbol{d}_k = -\nabla f(\boldsymbol{x}_k)
\end{array} \tag{2-7}
ステップ幅は$\alpha_k=1$とすることが多い。
以下で表される2次近似を最小化する方向、すなわち $\nabla f_k^Q(\boldsymbol{d})=\boldsymbol{0}$ が成り立つ $\boldsymbol{d}$ 方向に降下している。
f(\boldsymbol{x}_k+\boldsymbol{d})\approx f_k^Q(\boldsymbol{d})=f(\boldsymbol{x}_k)+\nabla f(\boldsymbol{x}_k)\cdot\boldsymbol{d}+\frac{1}{2}\nabla^2 f(\boldsymbol{x}_k)\boldsymbol{d}\cdot\boldsymbol{d}
ヘッセ行列$\nabla^2 f(\boldsymbol{x})$が正定値でないと大域的収束性がないという問題がある。
2.1.2.3. 準Newton法
Newton法のヘッセ行列$\nabla^2 f(\boldsymbol{x}_k)$を適当な正定値対称行列$B_k$に置き換える。
\begin{array}
~\boldsymbol{x}_{k+1}=\boldsymbol{x}_k +\alpha_k \boldsymbol{d}_k \\
B_k\boldsymbol{d}_k = -\nabla f(\boldsymbol{x}_k)
\end{array} \tag{2-8}
ステップ幅$\alpha_k$は、直線探索によって求める。
適当な正定値対称行列$B_k$は、BFGS公式やDFP公式のB公式などによって更新する場合や、逆行列$B_k^{-1}$を直接更新する場合 (H公式) がある。
大域的収束性が保証される。
2.1.2.4. 信頼領域法
更新量$\boldsymbol{s}_k$を、$f$の2次近似に関する以下の2次計画問題を解くことで求める。ただし、$\Delta_k>0$は信頼半径と呼ばれるハイパラで、2次近似がよい近似になる範囲を示す。
\begin{array}[ll]
&\min &f_k^Q(\boldsymbol{s})=f(\boldsymbol{x}_k)+\nabla f(\boldsymbol{x}_k) \cdot \boldsymbol{s}+\frac{1}{2}B_k\boldsymbol{s}\cdot\boldsymbol{s} \\
s.t. &\lVert\boldsymbol{s}\rVert \leq \Delta_k
\end{array} \tag{2-10} \label{2.44}
定数$c_1\in(0,1)$について、$\boldsymbol{s}_k$が以下の条件を満たすか考える (更新により関数値が十分に減少するか否かを調べている)。
f(\boldsymbol{x}_k+\boldsymbol{s}_k)\leq f(\boldsymbol{x}_k)+c_1(f_k^Q(\boldsymbol{s}_k)-f\left(\boldsymbol{x}_k)\right)
満たす場合、現在の点$\boldsymbol{x}$を以下の更新公式にしたがって点$\boldsymbol{x}_{k+1}$に更新する。
\boldsymbol{x}_{k+1}=\boldsymbol{x}_k +\boldsymbol{s}_k \tag{2-11} \label{2.45}
満たさない場合、$\Delta_k$をより小さい値に更新する。
大域的収束性が保証される。
2.2. 等式制約下での最適化
等式制約のみがある場合。
\begin{array}[lll]
&\min &f(\boldsymbol{x}) \\
s.t. &h_l(\boldsymbol{x})=0, &l=1,\cdots,r
\end{array} \tag{2-12} \label{2.48}
2.2.1. 最適性条件
Lagrangeの未定乗数法。最適解においては、$\nabla f(\boldsymbol{x})$は$\nabla h_1(\boldsymbol{x}),\cdots,\nabla h_l(\boldsymbol{x})$の1次結合で表される。1次結合で表せない場合、$h_k(\boldsymbol{x})=0$ に沿って少し進めば、解を改善できてしまう。
\begin{eqnarray}
&L(\boldsymbol{x}, \boldsymbol{\mu})=f(\boldsymbol{x})-\sum_{l=1}^r \mu_lh_l(\boldsymbol{x}) \\
&\frac{\partial L}{\partial \boldsymbol{\mu}}=\boldsymbol{0} \\
&\frac{\partial L}{\partial \boldsymbol{x}}=\boldsymbol{0}
\end{eqnarray} \tag{2-13} \label{2.54}
2.3. 不等式制約下での最適化
式(${\ref{2.1}}$)に示した一般的な形。下に再掲。
\begin{array}[lll]
&\min &f(\boldsymbol{x}) \\
s.t. &g_i(\boldsymbol{x}) \leq 0, &i=1,\cdots,m, \\
&h_l(\boldsymbol{x})=0, &l=1,\cdots,r
\end{array} \tag{2-14} \label{2.1a}
2.3.1. KKT条件
1次独立制約想定・Slaterの制約条件・Mangasarian-Fromovitz制約想定などのもとでの議論。
\begin{eqnarray}
&L(\boldsymbol{x},\boldsymbol{\lambda}, \boldsymbol{\mu})=f(\boldsymbol{x})+\sum_{i=1}^{m} \lambda_i g_i(\boldsymbol{x})+\sum_{l=1}^r \mu_lh_l(\boldsymbol{x}), \\
&\nabla L(\boldsymbol{x},\boldsymbol{\lambda},\boldsymbol{\mu})=\boldsymbol{0}, \\
&g_i(\boldsymbol{x})\leq 0,~~\lambda_i \geq 0,~~\lambda_i g_i(\boldsymbol{x})=0,~~~~~i=1,\cdots,m, \\
&h_l(\boldsymbol{x})=0,~~~~~l=1,\cdots,r
\end{eqnarray} \tag{2-15} \label{2.60}
最適解においては、目的関数の勾配は、有効な不等式制約の勾配と等式制約の勾配との1次結合で表される。非有効な場合 ($g_i(\boldsymbol{x})<0$の場合) は$\lambda_i=0$とすることで、ラグランジュ関数に組み込まれないようになっている。
2.3.2. 解法
2.3.2.1. ペナルティ法
目的関数に制約のペナルティ関数 (制約が満たされる場合は0をとり、満たされない場合には正の値を取る関数) を加えた関数 $\phi_{\rho}(\boldsymbol{x})$ を考える。
\phi_{\rho}(\boldsymbol{x})=f(\boldsymbol{x})+\rho\sum_{i=1}^{m}\left(\max\left\{g_i(\boldsymbol{x}),0\right\}\right)^2+\rho\sum_{l=1}^r h_l(\boldsymbol{x})^2 \tag{2-16} \label{2.68}
各反復では固定した $\rho$ に対し式(${\ref{2.68}}$)を目的関数とする無制約最適化問題を解き、反復ごとに$\rho$の値を徐々に大きくしていく。
$\rho$が有限な限り正確な最適解は得られない。
$\rho$が大きくなるにしたがって$\phi_{\rho}$のヘッセ行列の条件数が非常に大きくなり、無制約最適化問題を解くことが困難になることが多い。これを解決したのが乗数法。
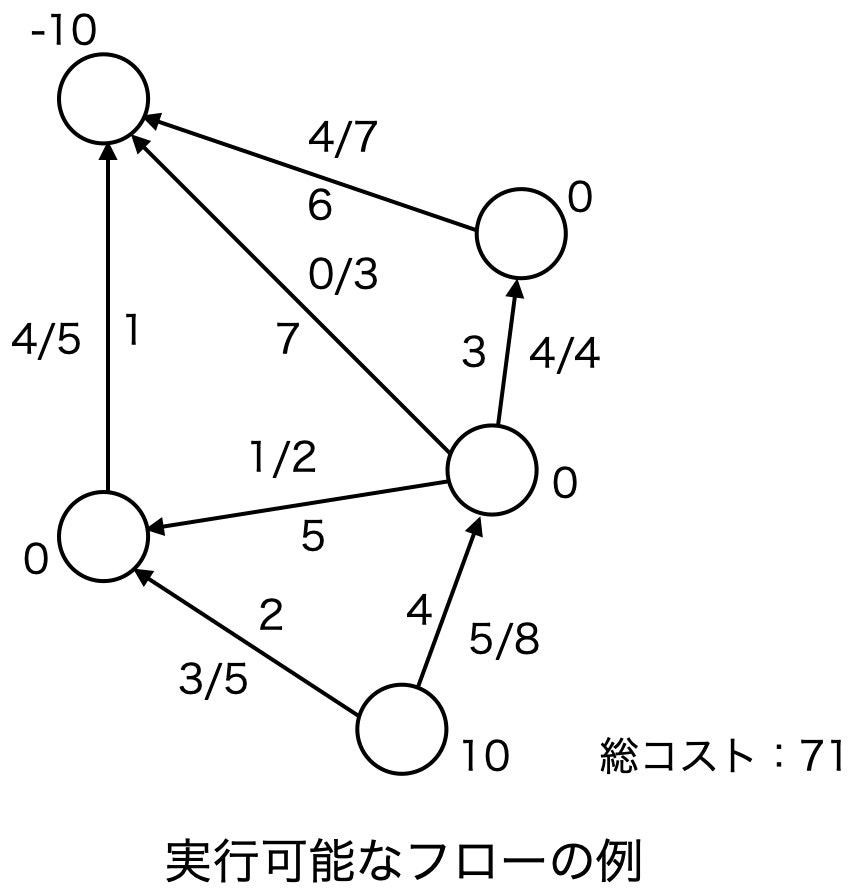
下の図は、以下の問題にペナルティ法を用いた例である。
\begin{array}
&\min &x+1 \\
s.t. &x\geq 0 \\
&\phi_{\rho}(x)=x+1+\rho(\max\lbrace -x,0\rbrace)^2
\end{array}
2.3.2.2. バリア関数法
目的関数に制約のバリア関数 (制約が満たされる点では有限の値をとり、制約の境界で無限大になる関数) を加えた関数 $\psi_\nu(\boldsymbol{x})$ を考える。
\psi_\nu(\boldsymbol{x})=f(\boldsymbol{x})-\nu\sum_{i=1}^{m}\log(-g_i(\boldsymbol{x})) \tag{2-17} \label{2.69}
下の問題の実行可能領域の内点を初期点として、各反復では固定した $\nu>0$ に対して $\psi_\nu(\boldsymbol{x})$ の無制約最小化問題を解き、反復ごとに $\nu$ の値を徐々に小さくすることで、最終的にもとの問題の最適解を得る。
初期点として必要な実行可能領域の内点が必ずしも容易に得られないことや、実行可能領域の境界に近づくにつれて $\psi_\nu(\boldsymbol{x})$ が悪条件となり解くことが難しいなどの欠点がある。主双対内点法が洗練され再び注目を集めている。
2.3.2.3. 逐次2次計画法
各反復において以下の2次最適化問題 (部分問題) を解き、その最適解 $\Delta\boldsymbol{x}$ を探索方向とする。$B_k$ はラグランジュ関数のヘッセ行列、あるいはその適当な近似行列。
\begin{array}[ll]
&\min &\frac{1}{2}B_k\Delta\boldsymbol{x}\cdot\Delta\boldsymbol{x}+\nabla f(\boldsymbol{x}_k)\cdot\Delta\boldsymbol{x} \\
s.t. &g_i(\boldsymbol{x}_k)+\nabla g_i(\boldsymbol{x}_k)\cdot\Delta\boldsymbol{x}\leq0, &i=1,\cdots,m \\
&h_l(\boldsymbol{x}_k)+\nabla h_l(\boldsymbol{x}_k)\cdot\Delta\boldsymbol{x}=0, &l=1,\cdots,r
\end{array} \tag{2-18} \label{2.71}
部分問題(${\ref{2.71}}$)のKKT条件が、もとの問題のKKT条件を $(\boldsymbol{x}_k, \boldsymbol{\lambda_k}, \boldsymbol{\mu}_k)$ において近似したものとなることが理論的根拠。
なお、ステップ幅 $\alpha_k$ はメリット関数を用いた直線探索によって決定する。メリット関数には、ペナルティ関数を用いた関数がしばしば用いられる。
2.3.2.4. 主双対内点法
$k$ 回目の探索において、以下の非線形方程式を適当な精度 (多くは1次近似) で満たす近似解 $(\Delta\boldsymbol{x}_k, \Delta\boldsymbol{\lambda}_k, \Delta\boldsymbol{\mu}_k)$ を探索方向とする。直線探索でステップ幅を求めて解を更新したら、$k+1$ 回目の反復では $\nu>0$ を小さい値に更新して同様の探索を行う。バリア関数の軌跡を近似的に辿るイメージ。
\begin{array}
~\nabla f(\boldsymbol{x}) - \boldsymbol{\lambda} + \sum_{i=1}^{r}\mu_l ~
\nabla h_l(\boldsymbol{x})=\boldsymbol{0} \\
h_l(\boldsymbol{x})=0, &l=1,\cdots,r \\
x_j\lambda_j=\nu,&j=1,\cdots,n \\
x_j>0,~~~~\lambda_j>0, &j=1,\cdots,n
\end{array} \tag{2-19} \label{2.75}
理論的根拠は以下。元の問題(${\ref{2.1a}}$)にスラック変数などを導入し、等式制約のみの問題に変換する。
\begin{array}[ll]
&\min &f(\boldsymbol{x}) \\
s.t. &h_l(\boldsymbol{x})=0, &l=1,\cdots,r \\
&\boldsymbol{x}\geq\boldsymbol{0}
\end{array} \tag{2-20} \label{2.74}
さらに、非負制約に関してバリア関数を導入し、以下の問題に変換する。
\begin{array}[ll]
&\min &f(\boldsymbol{x})-\nu\sum_{j=1}^{n}\log x_j \\
s.t. &h_l(\boldsymbol{x})=0, &l=1,\cdots,r \\
&\boldsymbol{x}>\boldsymbol{0}
\end{array} \tag{2-21} \label{2.74b}
この問題のKKT条件が、解くべき非線形方程式(${\ref{2.75}}$)である。$\nu→0$のとき、元の問題のKKT条件と一致する。
線形計画問題・半正定値計画問題に対しては、大域的最適解への収束が保証された多項式時間アルゴリズムである。一般の非線形計画問題に対しては、局所最適解への大域的収束性と局所的に十分速い収束のみが理論的に保証されている。
最適解の近くでもそれほど悪条件とならないことが、内点法からの改善点。
2.3.2.5. 乗数法 (拡張ラグランジュ関数法)
スラック変数等の導入により等式制約のみとした問題を考える。$k$ 回目の反復において、以下のとおり定義した拡張ラグランジュ関数の無制約最小化問題を、ラグランジュ乗数 $\boldsymbol{\mu}_k$ を固定して解いて解 $\boldsymbol{x}_k$ を得る。
L_{\sigma}(\boldsymbol{x}, \boldsymbol{\mu})=f(\boldsymbol{x})+\sum_{l=1}^{r}\mu_lh_l(\boldsymbol{x})+\frac{\sigma}{2}\sum_{l=1}^{r}h_l(\boldsymbol{x})^2 \tag{2-22} \label{2.78}
$k+1$ 回目の反復では $\boldsymbol{\mu}_{k+1}$ を以下のように更新して固定し、再度拡張ラグランジュ関数の無制約最小化問題を解く。
\boldsymbol{\mu}_{k+1}=\boldsymbol{\mu}_k+\sigma\boldsymbol{h}(\boldsymbol{x}_k) \tag{2-23} \label{2.79b}
また、等式制約の残差が1つ前の反復と比べて十分に減少しなかった場合は、$\sigma$ をより大きな値にする。
以下の命題が理論的根拠。十分大きい $\sigma$ をとれば、元の問題の局所最適解を求める問題を、$L_{\sigma}(\boldsymbol{x}, \bar{\boldsymbol{\mu}})$ の極小解を求める問題に変換できると主張している。
点 $\bar{\boldsymbol{x}}$ を元の問題の局所最適解とし、対応するラグランジュ乗数を $\bar{\boldsymbol{\mu}}$ とおく。$\bar{\boldsymbol{x}}$ において線型独立制約想定が成り立ち、$\bar{\boldsymbol{x}}$ と $\bar{\boldsymbol{\mu}}$ が2次の最適性条件を満たすことを仮定する。このとき、実数 $\hat{\sigma}>0$ が存在して、$\sigma \geq\hat{\sigma}$ を満たす任意の $\sigma$ に対して $\bar{\boldsymbol{x}}$ は $L_{\sigma}(\boldsymbol{x}, \bar{\boldsymbol{\mu}})$ の極小解である。
なお、式(${\ref{2.79b}}$)は、拡張ラグランジュ関数の1次の最適性条件と元の問題の1次の最適性条件を比較することで得られる。$\boldsymbol{\mu}_k$ を上の命題の $\bar{\boldsymbol{\mu}}$ に近づけるための操作。
2.4. 変分不等式
KKT条件は相補性問題の形で表されるため、相補性問題や変分不等式問題は最適化問題を一般化した問題とみなせる。
2.4.1. 相補性問題
以下の条件を満たすベクトル $\boldsymbol{x}$ を求める問題。
\boldsymbol{x}\geq\boldsymbol{0},~~~~~\boldsymbol{F}(\boldsymbol{x})\geq\boldsymbol{0}~~~~~\boldsymbol{F}(\boldsymbol{x}) \cdot\boldsymbol{x}=0 \tag{2-24} \label{2.87}
$\boldsymbol{x}\geq\boldsymbol{0}$ より、3つ目の条件は、以下の条件と等価。
F_j(\boldsymbol{x})x_j=0,~~~~~j=1, \cdots,n \tag{2-25} \label{2.87b}
以下のように記述することもある。
\boldsymbol{0}\leq\boldsymbol{x}\perp\boldsymbol{F}(\boldsymbol{x})\geq\boldsymbol{0} \tag{2-26} \label{2.87c}
$\boldsymbol{F}$ が線形のとき線形相補性問題、そうでないとき非線形相補性問題と呼ぶ。
一部の変数のみに非負制約と相補性条件を課す問題を混合相補性問題と呼ぶ。非線形計画問題のKKT条件は、$(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu})$ を変数とする混合相補性問題である。また、線形計画問題や凸2次計画問題の最適性条件は、(混合) 線形相補性問題である。
2.4.2. 変分不等式問題
以下の条件を満たす $\boldsymbol{x}$ を求める問題。
\boldsymbol{x}\in S,~~~~~\boldsymbol{F}(\boldsymbol{x}) \cdot(\boldsymbol{y}-\boldsymbol{x})\geq 0~~~~\forall y\in S \tag{2-27} \label{2.91}
$S=K(\boldsymbol{x})$ と書ける場合は凖変分不等式という。さらに $\boldsymbol{F}(\boldsymbol{x})=\boldsymbol{0}$ の場合は条件 $\boldsymbol{x}\in K(\boldsymbol{x})$を満たす $\boldsymbol{x}$、すなわち $K$ の不動点を求める問題に帰着する。
また、$S=\mathbb{R}^n$ の場合は、非線形方程式 $\boldsymbol{F}(\boldsymbol{x})=\boldsymbol{0}$ の解 $\boldsymbol{x}$ を求める問題になる ($\boldsymbol{y}=\boldsymbol{x}-\boldsymbol{F}(\boldsymbol{x})$ を選ぶと、2つ目の条件が $-\boldsymbol{F}(\boldsymbol{x})^T\boldsymbol{F}(\boldsymbol{x})\geq 0$ となるため)。
また、$S= \lbrace \boldsymbol{x}\in\mathbb{R}^n~| ~\boldsymbol{x}\geq\boldsymbol{0} \rbrace$ のとき、$\boldsymbol{x}$ が変分不等式問題 (${\ref{2.91}}$) の解であることと、相補性問題 (${\ref{2.87}}$) の解であることとは、同値である。すなわち、変分不等式問題は相補性問題を一般化した問題。
2.4.3. 方程式への再定式化
以下の条件を満たす関数 $\psi$ を相補性関数と呼び、相補性問題を非線形方程式へ再定式化できる。
\psi(x_j,s_j)=0~~\Leftrightarrow~~ x_j\geq0,~s_j\geq0,~x_js_j=0 \tag{2-28} \label{2.95b}
相補性関数の例としては、以下のフィッシャー・ブアマイスター関数がある。
\psi_{FB}(a,b)=\sqrt{a^2+b^2}-(a+b) \tag{2-29} \label{2.96}
また、閉凸集合 $S$ に対して、$S$ に属する点のうちで点 $\boldsymbol{z}$ からの距離が最小になるものを $\boldsymbol{z}$ の $S$ への射影と呼び、$\boldsymbol{P}_S(\boldsymbol{z})$ で表す。変分不等式問題は、射影を用いて以下のように再定式化できる。
\boldsymbol{x}-\boldsymbol{P}_S(\boldsymbol{x}-\boldsymbol{F}(\boldsymbol{x}))=\boldsymbol{0} \tag{2-30} \label{2.100}
理論的根拠は以下。$S$ が空でない閉凸集合であるとき、任意の点 $\boldsymbol{z}$ に対して $\boldsymbol{P}_S(\boldsymbol{z})$ は一意的に存在し、以下の条件を満たす。
(\boldsymbol{y}-\boldsymbol{P}_S(\boldsymbol{z}))^T(\boldsymbol{P}_S(\boldsymbol{z})-\boldsymbol{z})\geq0~~~~~\forall\boldsymbol{y}\in S \tag{2-31} \label{2.98}
$\boldsymbol{z}=\boldsymbol{x}-\boldsymbol{F}(\boldsymbol{x})$ とおいて、元の変分不等式問題と比べることで導かれる。
相補性問題や変分不等式問題を再定式化することで導かれる非線形方程式は、一般に微分不可能な点を含む。そのため、通常のNewton法を用いることはできず、工夫が必要である。
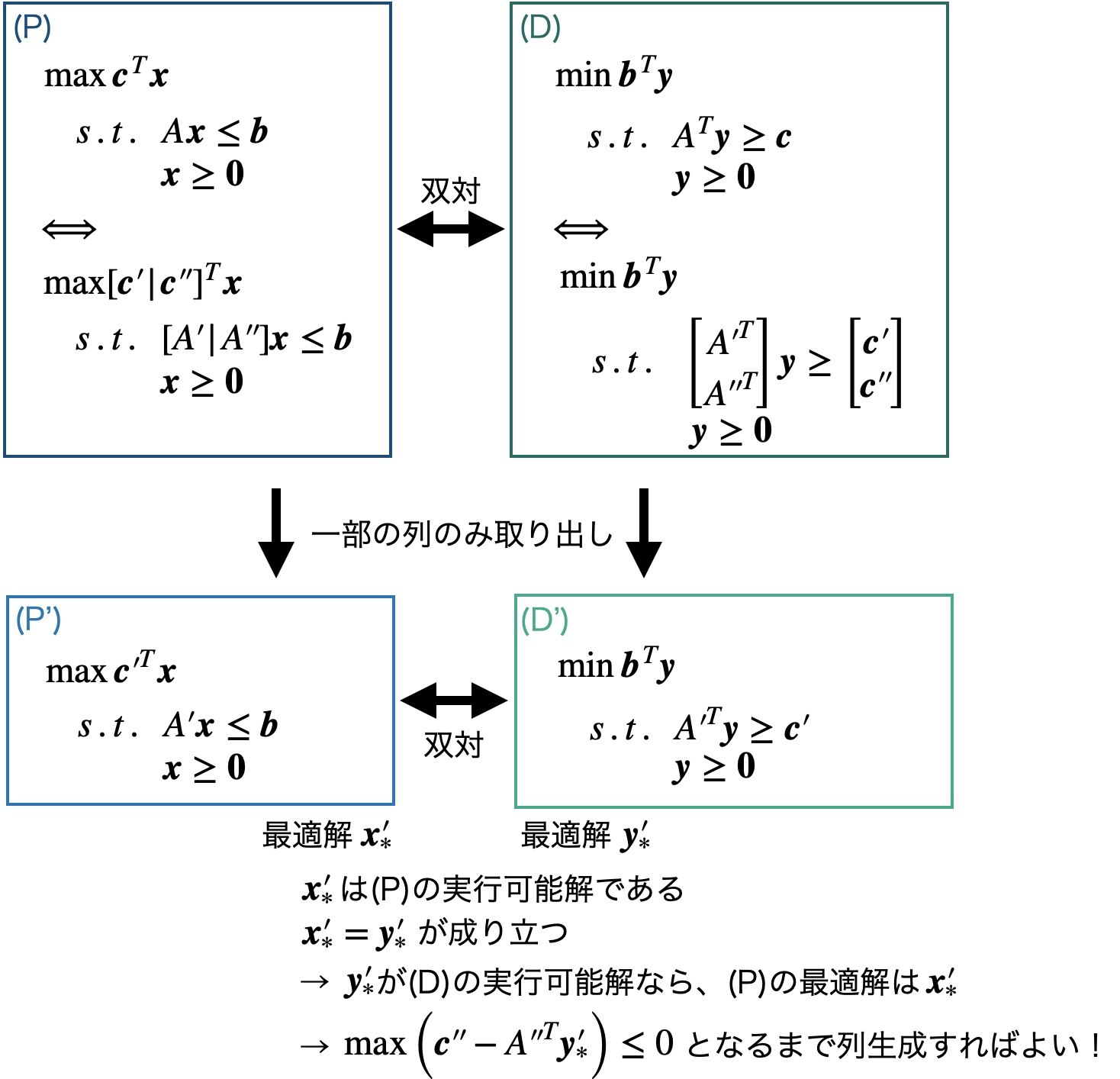
3. 双対理論
3.1 凸集合と凸関数
3.1.1 凸集合
集合 $S \subseteq \mathbb{R}^n$ が凸集合であるとは、任意の点 $\boldsymbol{x},\boldsymbol{y}\in S$ に対して以下の条件が満たされることをいう。
\lambda\boldsymbol{x}+(1-\lambda)\boldsymbol{y}\in S,~~~~~\forall\lambda\in[0,1] \tag{3-1} \label{3.0}
直観的には、凹んでない集合。
また、点 $\boldsymbol{x}_1,\cdots,\boldsymbol{x}_k\in\mathbb{R}^n$ が与えられたとき、条件
\sum_{i=1}^k\lambda_i=1,~~~~~\lambda_1,\cdots,\lambda_k\geq0 \tag{3-2} \label{3.1}
を満たす実数 $\lambda_1,\cdots,\lambda_k$ を用いて、以下のように表せる点 $\boldsymbol{x}$ を $\boldsymbol{x}_1,\cdots,\boldsymbol{x}_k$ の凸結合と呼ぶ。
\boldsymbol{x}=\sum_{i=1}^k\lambda_k\boldsymbol{x}_i \tag{3-3} \label{3.1b}
3.1.2 錐
空でない集合 $C\subseteq\mathbb{R}^n$ のうち、任意の元 $\boldsymbol{x}\in C$ と任意の実数 $\lambda\geq 0$ に対して条件 $\lambda\boldsymbol{x}\in C$ を満たすものを錐と呼ぶ。凸集合であるような錐を凸錐といい、閉集合であるような凸錐を閉凸錐という。
点 $\boldsymbol{x}_1,\cdots,\boldsymbol{x}_k\in\mathbb{R}^n$ が与えられたとき、非負の実数 $\lambda_1,\cdots,\lambda_k\geq 0$ を用いて以下のように表せる点 $\boldsymbol{x}$ を点 $\boldsymbol{x}_1,\cdots,\boldsymbol{x}_k$ の錐結合と呼ぶ。
\boldsymbol{x}=\sum_{i=1}^{k}\lambda_i\boldsymbol{x}_i \tag{3-4} \label{3.3b}
また、以下の集合 $C_2$ は凸錐であり、2次錐と呼ぶ。
C_2= \left\{ (t,\boldsymbol{x})\in\mathbb{R}\times\mathbb{R}^n~|~t\geq\left(\sum_{j=1}^{n}|x_j|^2\right)^{1/2} \right\} \tag{3-5} \label{3.3c}
錐 $C\subseteq\mathbb{R}^n$ に対して、以下の集合 $C^\circ\subseteq\mathbb{R}^n$ は錐であり、極錐と呼ぶ。
C^\circ=\lbrace\boldsymbol{s}\in\mathbb{R}^n~|~\boldsymbol{s}^T\boldsymbol{x}\leq0,~~\forall\boldsymbol{x}\in C\rbrace \tag{3-6}
また、集合 $S$ の接ベクトルの集合を $S$ の点 $\boldsymbol{x}$ における接錐と呼び、$T_S(\boldsymbol{x})$ と書く。接錐 $T_S(\boldsymbol{x})$ の極錐 $T_S(\boldsymbol{x})^\circ$ を点 $\boldsymbol{x}$ における $S$ の法線錐と呼び、$N_S(\boldsymbol{x})$ で表す。

3.1.3 凸関数
関数 $f:\mathbb{R}^n→\mathbb{R}\cup \lbrace +\infty \rbrace$ が凸関数であるとは、任意の点 $\boldsymbol{x}, \boldsymbol{y}\in\mathbb{R}^n$ に対して以下の条件が成り立つことである。
\lambda f(\boldsymbol{x})+(1-\lambda)f(\boldsymbol{y})\geq f(\lambda\boldsymbol{x}+(1-\lambda)\boldsymbol{y}),~~~~~\forall\lambda\in [0,1] \tag{3-7} \label{3.4}
関数 $f$ が凸関数であるための必要十分条件は、$f$ のヘッセ行列 $\nabla^2f(\boldsymbol{x})$ が半正定値であること。
3.2 劣勾配
凸関数 $f$ と点 $\boldsymbol{x}$ に対して、以下の条件を満たす $\boldsymbol{s}\in\mathbb{R}^n$ を、$f$ の $\boldsymbol{x}$ における劣勾配と呼ぶ。
f(\boldsymbol{y})\geq f(\boldsymbol{x})+\boldsymbol{s}\cdot (\boldsymbol{y}-\boldsymbol{x}),~~~~~\forall\boldsymbol{y}\in\mathbb{R}^n \tag{3-8} \label{3.10}
また、劣勾配全体の集合を劣微分 $\partial f(\boldsymbol{x})$ と呼ぶ。
\partial f(\boldsymbol{x})= \left\{ \boldsymbol{s}\in\mathbb{R}^n~|~f(\boldsymbol{y})\geq f(\boldsymbol{x})+\boldsymbol{s}\cdot(\boldsymbol{y}-\boldsymbol{x}) \right\} \tag{3-9} \label{3.11}
$f$ が点 $\boldsymbol{x}$ において微分可能な場合には、$\partial f(\boldsymbol{x})= \lbrace \nabla f(\boldsymbol{x}) \rbrace$ が成り立つ。
$\boldsymbol{s}\in \partial f(\boldsymbol{x})$ が成り立つことは、$\boldsymbol{x}\in\arg\max_{\boldsymbol{y}}\lbrace\boldsymbol{s}\cdot\boldsymbol{y}-f(\boldsymbol{y})~|~\boldsymbol{y}\in\mathbb{R}^n\rbrace$ が成り立つことと同値。
「任意の $\boldsymbol{x}$ において $f(\boldsymbol{x})$ 以下となるような接超平面の勾配」というイメージ。

3.3 分離定理
ベクトル $\boldsymbol{h}\neq\boldsymbol{0}\in\mathbb{R}^n$ とスカラー $g\in\mathbb{R}$ を用いて定義される以下の集合 $H(\boldsymbol{h},g)$ を、$\boldsymbol{h}$ と $g$ が定める超平面と呼ぶ。
※ $\boldsymbol{h}$ と $\boldsymbol{x}$ の内積が一定 = $\boldsymbol{h}$ への $\boldsymbol{x}$ の正射影が一定 = 超平面
H(\boldsymbol{h},g)=\lbrace\boldsymbol{x}\in\mathbb{R}^n~|~\boldsymbol{h}^T\boldsymbol{x}=g\rbrace \tag{3-10} \label{3.12b}
また、以下の集合 $H^+(\boldsymbol{h}, g),~H^-(\boldsymbol{h},g)$ を、超平面 $H(\boldsymbol{h},g)$ が定義する半空間と呼ぶ。
\begin{align}
H^+(\boldsymbol{h}, g)=\lbrace\boldsymbol{x}\in\mathbb{R}^n~|~\boldsymbol{h}^T\boldsymbol{x}\geq g\rbrace \tag{3-10} \label{3.12c} \\
H^-(\boldsymbol{h}, g)=\lbrace\boldsymbol{x}\in\mathbb{R}^n~|~\boldsymbol{h}^T\boldsymbol{x}\leq g\rbrace \tag{3-11} \label{3.12d}
\end{align}
集合 $S_1,S_2$ に対して条件 $S_1\subseteq H^+(\boldsymbol{h}, g),~S_2\subseteq H^-(\boldsymbol{h}, g)$ が成り立つとき、超平面 $H(\boldsymbol{h}, g)$ を $S_1$ と $S_2$ の分離超平面という。

分離定理は以下。
2つの空でない凸集合 $S_1, S_2\subseteq\mathbb{R}^n$ が $S_1\cap S_2=\emptyset$ を満たすならば、$S_1$ と $S_2$ の分離超平面が存在する。すなわち、以下の条件を満たす $\boldsymbol{s}\in\mathbb{R}^n$ が存在する。
\inf\lbrace\boldsymbol{s}^T\boldsymbol{x}~|~\boldsymbol{x}\in S_1\rbrace \geq \sup\lbrace\boldsymbol{s}^T\boldsymbol{x}~|~\boldsymbol{x}\in S_2\rbrace \tag{3-12} \label{3.12e}
さらに、$S_1$ と $S_2$ が閉集合で少なくとも一方が有界なら、以下の条件を満たす $\boldsymbol{s}\in\mathbb{R}^n$ が存在する。
\inf\lbrace\boldsymbol{s}^T\boldsymbol{x}~|~\boldsymbol{x}\in S_1\rbrace > \sup\lbrace\boldsymbol{s}^T\boldsymbol{x}~|~\boldsymbol{x}\in S_2\rbrace \tag{3-13} \label{3.12f}
分離定理より、線形計画問題などの最適性条件において重要な役割を果たすファルカスの補題が得られる。
定行列 $A\in\mathbb{R}^{m\times n}$ と定ベクトル $\boldsymbol{b}\in\mathbb{R}^m$ に対して、次のいずれか一方のみが必ず成り立つ。
(a) $A\boldsymbol{x}=\boldsymbol{b},~\boldsymbol{x}\geq\boldsymbol{0}$ を満たす $\boldsymbol{x}\in\mathbb{R}^n$ が存在する。
(b) $A^T\boldsymbol{y}\geq \boldsymbol{0},~\boldsymbol{b}^T\boldsymbol{y}<0$ を満たす $\boldsymbol{y}\in\mathbb{R}^m$ が存在する。
3.4 ルシャンドル変換と共役関数
関数 $f$ に対して、以下で定義される関数 $f^* $ を $f$ の共役関数と呼ぶ。また、写像 $f→f^* $ をルシャンドル変換と呼ぶ。
f^*(\boldsymbol{s})= \sup\lbrace\boldsymbol{s}\cdot\boldsymbol{x}-f(\boldsymbol{x})~|~\boldsymbol{x}\in\mathbb{R}^n\rbrace \tag{3-14} \label{3.14}
普通に $\max_{\boldsymbol{x}}\lbrace\boldsymbol{s}\cdot\boldsymbol{x}-f(\boldsymbol{x})\rbrace$ を考えると分かりやすい。
$\nabla(\boldsymbol{s}\cdot\boldsymbol{x}-f(\boldsymbol{x}))=\boldsymbol{s}-\nabla f(\boldsymbol{x})=\boldsymbol{0}$ すなわち $\nabla f(\boldsymbol{x})=\boldsymbol{s}$ を満たす $\boldsymbol{x}$ が$f^* (\boldsymbol{s})$ の値。
幾何的には、勾配 $\boldsymbol{s}$ の $f(\boldsymbol{x})$ の接平面と $z$ 軸との交点が $-f^* (\boldsymbol{s})$。

凸関数と劣微分の間には、以下のような関係がある。次の3つの条件は互いに等価。
(a) $\boldsymbol{s}\in\partial f(\boldsymbol{x})$
(b) $f(\boldsymbol{x})+f^* (\boldsymbol{s})=\boldsymbol{s}\cdot\boldsymbol{x}$
(c) $\boldsymbol{x}\in\partial f^* (\boldsymbol{s})$
3.5 最適性条件
以下の問題を考える。
\begin{align}
&\min &f(\boldsymbol{x}) \\
&s.t. &\boldsymbol{x}\in S
\end{align} \tag{3-15} \label{3.24}
$f$ が微分可能とする。点 $\bar{\boldsymbol{x}}\in S$ が問題 $(\ref{3.24})$ の局所最適解ならば、以下が成立する。そのような $\bar{\boldsymbol{x}}$ を停留点という。
-\nabla f(\boldsymbol{x})\in N_S(\bar{\boldsymbol{x}}) \tag{3-16} \label{3.25}
以下のイメージ。制約条件が微分可能な場合は、法線錐 $N_S(\boldsymbol{x})$ が制約条件の勾配の1次結合で表せる範囲であることであり、KKT条件と一致することが分かる。

3.6 双対問題
3.6.1 Fenchel双対性
$f, g$ が閉真凸関数、$A$ を定行列としたとき、以下の凸計画問題を考える。
(P_F):~~~~\min_{\boldsymbol{x}}~f(\boldsymbol{x})+g(A\boldsymbol{x}) \tag{3-17} \label{3.25b}
このとき、以下の最大化問題をFenchel双対問題という。これも凸計画問題。
(D_F):~~~~\max_{\boldsymbol{w}}~-f^*(A^T\boldsymbol{w})-g^*(-\boldsymbol{w}) \tag{3-18} \label{3.25c}
以下の命題が成り立つ。
問題($P_F$)と問題(D_F)の双方に最適解が存在して以下が成り立つことを仮定する。
-\infty <\min (P_F)=\max (D_F)<\infty \tag{3-19} \label{3.30b}
このとき、$\bar{\boldsymbol{x}}\in\mathbb{R}^n$ および $\bar{\boldsymbol{w}}\in\mathbb{R}^m$ が問題($P_F$)と問題($D_F$)の最適解であるための必要十分条件は、以下が成り立つことである。
\begin{align}
A^T\bar{\boldsymbol{w}}\in\partial f(\bar{\boldsymbol{x}}) \\
-\bar{\boldsymbol{w}}\in\partial g(A\bar{\boldsymbol{x}})
\end{align} \tag{3-20} \label{3.30c}
3.6.2 Lagrange双対性
以下の問題を考える。
\begin{align}
&\min &f(\boldsymbol{x}) \\
&s.t. &g_i(\boldsymbol{x})\leq 0,~~~~~&i=1,\cdots,m \\
&&h_l(\boldsymbol{x})=0,~~~~~&l=1,\cdots,r
\end{align} \tag{3-21} \label{3.34b}
以下のとおりラグランジュ関数を定義。
L(\boldsymbol{x},\boldsymbol{\lambda},\boldsymbol{\mu})=\left\{
\begin{array}{ll}
f(\boldsymbol{x})+\sum_{i=1}^{m}\lambda_ig_i(\boldsymbol{x})+\sum_{l=1}^{r}\mu_l h_l(\boldsymbol{x}) &\mathrm{if}~~\boldsymbol{\lambda}\geq\boldsymbol{0} \\
-\infty &\mathrm{otherwise}
\end{array}
\right. \tag{3-22} \label{3.35c}
定義より、以下が成り立つ。
\sup_{\boldsymbol{\lambda}}\lbrace L(\boldsymbol{x},\boldsymbol{\lambda},\boldsymbol{\mu}~|~\boldsymbol{\lambda}\in\mathbb{R}^m)\rbrace=\left\{
\begin{array}{ll}
f(\boldsymbol{x}) &\mathrm{if}~~g_i(\boldsymbol{x})\leq 0 \\
\infty &\mathrm{otherwise}
\end{array}
\right. \tag{3-23} \label{3.32b}
そのため、問題($\ref{3.34b}$)は、以下の問題と等価である。
(P_L):~~~~~\min_{\boldsymbol{x}}\sup_{\boldsymbol{\lambda}}\lbrace L(\boldsymbol{x}, \boldsymbol{\lambda},\boldsymbol{\mu})~|~\boldsymbol{\lambda}\in\mathbb{R}^m\rbrace \tag{3-24} \label{3.32c}
これに対して、最小化と最大化の順序を入れ替えた以下の問題を考える。この問題を元の問題($D_L$)のラグランジュ双対問題という。
(D_L):~~~~~\max_{\boldsymbol{\lambda}}\inf_{\boldsymbol{x}}\lbrace L(\boldsymbol{x}, \boldsymbol{\lambda},\boldsymbol{\mu})~|~\boldsymbol{\lambda}\in\mathbb{R}^m\rbrace \tag{3-25} \label{3.33}
これらの問題に対して、
\sup_{\boldsymbol{\lambda}} L(\boldsymbol{x}, \boldsymbol{\lambda},\boldsymbol{\mu})\geq L(\boldsymbol{x},\boldsymbol{\lambda},\boldsymbol{\mu})\geq \inf_{\boldsymbol{x}} L(\boldsymbol{x},\boldsymbol{\lambda},\boldsymbol{\mu}) \tag{3-26} \label{3.33b}
が成り立つことから、主問題とラグランジュ双対問題の間には以下のとおり弱双対性が成り立つ。
\inf (P_L)\geq\sup (D_L) \tag{3-27} \label{3.34}
以下では等式制約を省いて議論する。鞍点定理が成り立つ。鞍点とは、$L(\bar{\boldsymbol{x}},\boldsymbol{\lambda})\leq L(\bar{\boldsymbol{x}},\bar{\boldsymbol{\lambda}})\leq L(\boldsymbol{x},\bar{\boldsymbol{\lambda}})$ が成り立つ点 $(\bar{\boldsymbol{x}},\bar{\boldsymbol{\lambda}})$ である。双対ギャップが0の点は鞍点であることと、その逆を主張している。
点 $(\bar{\boldsymbol{x}},\bar{\boldsymbol{\lambda}})$ において、$L(\bar{\boldsymbol{x}},\bar{\boldsymbol{\lambda}})$ は有限であるとする。このとき、$(\bar{\boldsymbol{x}},\bar{\boldsymbol{\lambda}})$ が $L$ の鞍点であるための必要十分条件は、$\bar{\boldsymbol{x}}$ および $\bar{\boldsymbol{\lambda}}$ がそれぞれ($P_L$)および($D_L$)の最適解であり $\min (P_L)=\min (D_L)$ が成り立つことである。
また、以下の命題も成り立つ。微分可能な凸計画問題において、ラグランジュ双対問題の最適解は主問題の下限を定義することを主張している。
主問題($P_L$)において、目的関数 $f$ と制約関数 $g_1,\cdots,g_m$ が微分可能な凸関数であるとする。さらに、$\inf (P_L)$ が有限でSlater制約想定が満たされるとする。このとき、双対問題($D_L$)に最適解が存在し、$\inf (P_L)=\max (D_L)$ が成立する。
ラグランジュ双対問題の $\inf\lbrace L(\boldsymbol{x},\boldsymbol{\lambda},\boldsymbol{\mu}~|~\boldsymbol{x}\in\mathbb{R}^n)$ が扱いやすい形に書きくだせるかどうかは主問題の性質に依存する。下限値を厳密に求める代わりに1次の最適性条件を用いて得られる双対問題が、以下のウルフ双対問題である。
3.6.3 Wolfe双対問題
問題 ($\ref{3.34b}$) に対して以下の問題をウルフ双対問題という。
\begin{align}
&\min &L(\boldsymbol{x},\boldsymbol{\lambda},\boldsymbol{\mu}) \\
&s.t. &\nabla_{\boldsymbol{x}} L(\boldsymbol{x}, \boldsymbol{\lambda},\boldsymbol{\mu})=\boldsymbol{0} \\
&&\boldsymbol{\lambda}\geq\boldsymbol{0},~~\boldsymbol{\mu}\geq\boldsymbol{0}
\end{align} \tag{3-28} \label{3.35b}
ラグランジュ双対問題では変数が $\boldsymbol{\lambda}$ のみであったのに対して、ウルフ双対問題では主問題の変数 $\boldsymbol{x}$ も変数として含む。
また、ウルフ双対問題はFenchel双対問題やラグランジュ双対問題のような対称性を持たない。
4. 線形計画
4.1 線形計画問題
4.1.1 定義
いくつかの線形方程式や線形不等式を制約とし、線形関数を目的関数とする最適化問題。
\begin{array}
&\min &\sum_{j=1}^{n}c_jx_j \\
s.t. &\boldsymbol{a}_i^T\boldsymbol{x}=b_i, &i=1,\cdots,m \\
&x_j\geq 0, &j=1,\cdots,n
\end{array}
より簡潔な表記として以下がある。どのような線形計画問題も、適当な変形をすることで以下の形に書き直せる。
\begin{array}
&\min &\boldsymbol{c}^T\boldsymbol{x} \\
s.t. &A\boldsymbol{x}=\boldsymbol{b} \\
&\boldsymbol{x}\geq\boldsymbol{0}
\end{array} \tag{4-1} \label{4.2}
4.2 双対性
4.2.1 双対問題
主問題 ($\ref{4.2}$) に対して、以下の問題を双対問題という。
\begin{array}
&\max &\boldsymbol{b}^T\boldsymbol{y} \\
s.t. &A^T\boldsymbol{y}\leq\boldsymbol{c}
\end{array} \tag{4-2} \label{4.11}
スラック変数 $\boldsymbol{s}$ を導入して以下のようにも書ける。
\begin{array}
&\max &\boldsymbol{b}^T\boldsymbol{y} \\
s.t. &A^T\boldsymbol{y}+\boldsymbol{s}=\boldsymbol{c} \\
&\boldsymbol{s}\geq\boldsymbol{0}
\end{array}
線形計画では、双対問題の双対問題は主問題。
4.2.2 双対定理
以下のとおり弱双対定理が成り立つ。以下の性質を弱双対性という。
主問題 ($\ref{4.2}$) の任意の実行可能解 $\boldsymbol{x}$ と双対問題 ($\ref{4.11}$) の任意の実行可能解 $\boldsymbol{y}$ に対して、以下の不等式が成り立つ。
\boldsymbol{c}^T\boldsymbol{x}\geq\boldsymbol{b}^T\boldsymbol{y}
また、以下のとおり強双対定理が成り立つ。以下の性質を強双対性という。ファルカスの補題を使って証明できる。
主問題 ($\ref{4.2}$) と双対問題 ($\ref{4.11}$) がともに実行可能解を持つことと、両者に最適解が存在して最適値が一致することとは、同値である。
4.2.3 最適性条件
以下のとおり相補性定理が成り立つ。以下の条件を相補性条件という。
主問題 ($\ref{4.2}$) の実行可能解 $\boldsymbol{x}$ と双対問題 ($\ref{4.11}$) の実行可能解 $\boldsymbol{y}$ がそれぞれの問題の最適解であるための必要十分条件は、以下の条件が成り立つことである。
x_j(\boldsymbol{c}-A^T\boldsymbol{y})_j=0,~~~~~j=1,\cdots,n
最適解においては、主問題の不等式制約 $x_j\geq 0$ と双対問題の不等式制約 $(\boldsymbol{c}-A^T\boldsymbol{y})_j\geq 0$ の少なくとも一方が有効になることを表している。
また、以下が成り立つとき、解 $\boldsymbol{x}$ と $\boldsymbol{y}$ は狭義相補性を満たすという。主問題の不等式制約と双対問題の不等式制約のどちらか一方のみ有効になることを示している。
x_j(\boldsymbol{c}-A^T\boldsymbol{y})_j>0,~~~~~j=1,\cdots,n
最適解 $\boldsymbol{x}$ と $\boldsymbol{y}$ が狭義相補性を満たすとき、相補性条件から以下の連立方程式が得られ、最適解はその解となる。ただし、$N, B$ は未知なので、方程式を解けば解が求まるというわけではない点に注意。適当な $N, B$ を見つける問題になる (cf. 単体法)。
\begin{array}
&x_j=0, &j\in N \\
(\boldsymbol{c}-A^T\boldsymbol{y})_j=0, &j\in B
\end{array}
ただし、$N, B$ は $\lbrace 1,\cdots,n\rbrace$ の部分集合で $N\cup B =\lbrace 1,\cdots,n\rbrace$ および $N\cap B$ を満たす。
主問題・双対問題それぞれの最適解であるための必要十分条件は以下。
\begin{array}
&A\boldsymbol{x}=\boldsymbol{b} \\
A^T\boldsymbol{y}+\boldsymbol{s}=\boldsymbol{c} \\
x_js_j=0,~~~~~j=1,\cdots,n \\
\boldsymbol{x}\geq\boldsymbol{0},~~~~~\boldsymbol{s}\geq\boldsymbol{0}
\end{array}
4.3 単体法
実行可能基底解と呼ばれる点、すなわち実行可能領域の頂点を順々に辿ることで線形計画問題の最適解を得る方法。
4.3.1 基底解
$A$ の列を適当に並び替え、それに伴ってそれに伴って $\boldsymbol{x}$ の行も並び替え、以下のようにする。
A=\begin{bmatrix}
A_B~|~A_N
\end{bmatrix},~~~~~\boldsymbol{x}=\begin{bmatrix}
\boldsymbol{x}_B \\
\boldsymbol{x}_N
\end{bmatrix}
以下で定義されるベクトル $\hat{\boldsymbol{x}}$ を基底解と呼ぶ。基底解は等式制約を満たす。
\hat{\boldsymbol{x}}=\begin{bmatrix}
\hat{\boldsymbol{x}}_B \\
\hat{\boldsymbol{x}}_N
\end{bmatrix}=\begin{bmatrix}
A_B^{-1}\boldsymbol{b} \\
\boldsymbol{0}
\end{bmatrix}
$\hat{\boldsymbol{x}}_B\geq\boldsymbol{0}$ を満たす場合実行可能基底解と呼ぶ。実行可能領域の頂点を表す。
また、$\hat{\boldsymbol{x}}_B>\boldsymbol{0}$ のとき $\hat{\boldsymbol{x}}$ は非退化であるといい、そうでないとき退化しているという。
同様に $\boldsymbol{c}, \boldsymbol{s}$ も分割し、$\hat{\boldsymbol{y}}, \hat{\boldsymbol{s}}$ を以下のように定義する。
\begin{array}
&\hat{\boldsymbol{y}}=(A_B^{-1})^T\boldsymbol{c}_B \\
\hat{\boldsymbol{s}}_B=\boldsymbol{0} \\
\hat{\boldsymbol{s}}_N=\boldsymbol{c}_N-A_N^T(A_B^{-1})^T\boldsymbol{c}_B
\end{array}
以上で定義した $\hat{\boldsymbol{x}}$ と $(\hat{\boldsymbol{y}}, \hat{\boldsymbol{s}})$ は $\hat{\boldsymbol{s}}_N\geq\boldsymbol{0}$ のとき最適性条件を満たすため、主問題・双対問題の最適解となる。適当な $N, B$ を探すのが、単体法でやっていること。
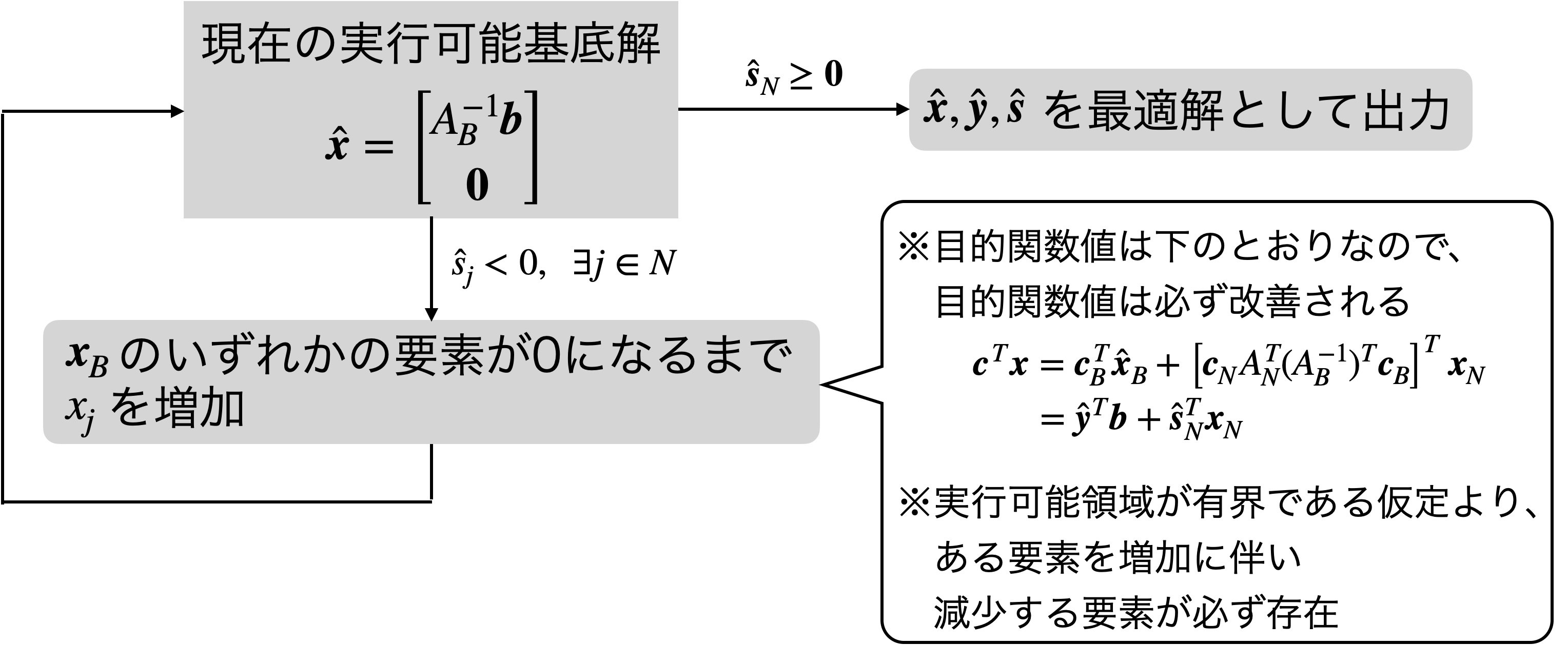
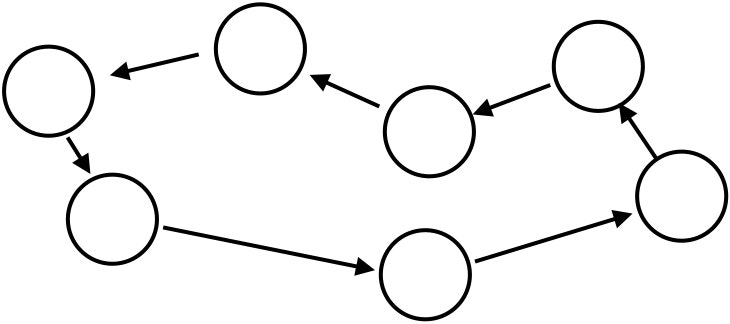
4.3.2 枢軸変換 (非退化な問題の場合)
主問題のすべての実行可能基底解が非退化であること (非退化仮定) と実行可能領域が有界であることを仮定した場合の手法。
1つの実行可能基底解から新しい実行可能基底解を生成する変換を枢軸変換という。以下の図の処理。
4.3.3 退化した問題の場合
非退化仮定が成り立たない場合、退化が繰り返し発生して同じ基底解に戻ってしまう現象 (巡回) が起こりうる。
枢軸変換における $x_j$ などの選び方を工夫することによって、単体法が有限回で終了し最適解が得られることが知られている。
具体的には、最小添字規則や辞書式規則がある。
4.3.4 2段階単体法
4.3.2節の枢軸変換は、主問題の実行可能基底解が分かっているときの手法。2段階単体法では、初期解となる実行可能基底解を見つけるために、まず別の線形計画問題を単体法で解くという方法。
第1段階では、以下の条件を満たす補助問題を作る。
①実行可能基底解のうちの1つが自明に分かっている
②最適解から主問題の実行可能基底解の情報が得られる。
例えば、以下のような問題。$\boldsymbol{x}_a$ は人工変数と呼ばれる。
\begin{array}
&\min &\boldsymbol{1}^T\boldsymbol{x}_a \\
s.t. &A\boldsymbol{x}+\boldsymbol{x}_a=\boldsymbol{b} \\
&\boldsymbol{x}\geq\boldsymbol{0},~~~~\boldsymbol{x}_a\geq\boldsymbol{0}
\end{array}
この問題は実行可能基底解 $(\boldsymbol{x},\boldsymbol{x}_a)=(\boldsymbol{0},\boldsymbol{b})$ をもち、得られた最適値が正の場合は、元の問題は実行可能解を持たない。逆に得られた最適値が0で最適解が $\boldsymbol{x}_a=\boldsymbol{0}$ を満たしていれば、そのときの $\boldsymbol{x}$ は元の問題の実行可能基底解となっているため、それを初期解として、元の問題に対して単体法を実行すればよい。
4.3.5 その他の単体法
- 双対単体法:線形計画問題の双対問題を解くことによって主問題の最適解を得る単体法。(主) 単体法は双対問題の制約と相補性条件を前提として主問題の制約を満たすような解を探す方法である一方、双対単体法は主問題の制約と相補性条件を前提として双対問題の制約を満たすような解を探す方法であると言える。
- ネットワーク単体法:$A$ がグラフの接続行列である場合は基底解をグラフ上の木と対応させることができるという性質を利用することで、効率的に単体法を実行する方法。
4.4 内点法
最適解に収束する内点実行可能解 (条件 $\boldsymbol{x}\geq\boldsymbol{0}$ および $\boldsymbol{s}\geq\boldsymbol{0}$ を満たす実行可能解) の点列を生成する解法であり、大規模な線形計画問題を解く際には単体法より優れているとされている。また、半正定値計画問題や2次錐計画問題などに一般化されている。
主問題の空間で点列を生成する主内点法と、主問題および双対問題の両方の空間に点列を生成する双対内点法とがある。
4.4.1 線形計画問題のサイズ
線形計画問題 ($\ref{4.2}$) において $A, \boldsymbol{b}, \boldsymbol{c}$ の各要素が整数であるとき、問題のサイズ $L$ は以下のとおり定義される。
L=\sum_{i=1}^{m}\sum_{j=1}^{n}\lceil\log_2 (|A_{ij}|+1)\rceil +\sum_{i=1}^{m}\lceil\log_2 (|b_i|+1)\rceil + \sum_{j=1}^{n}\lceil\log_2 (|c_j|+1)\rceil + mn+1
線形計画問題を解くために必要なビット演算の回数が $L, m, n$ の多項式で抑えられるアルゴリズムを、線形計画問題に対する多項式時間アルゴリズムという。
また、線形計画問題のサイズ $L$ を用いて、最適解の大きさや最適値について以下のとおり評価できる。
- 主問題 ($\ref{4.2}$) および双対問題 ($\ref{4.11}$) に最適解が存在するならば、最適解の中には $x_1,\cdots,x_n,y_1,\cdots,y_m$ の絶対値がすべて $2^L$ 以下のものが存在する。
- 主問題 ($\ref{4.2}$) および双対問題 ($\ref{4.11}$) に対して最適値との差が $2^{-L}$ 以下の近似解が得られたら、その近似解を利用して厳密解を多項式時間で求めることができる。
4.4.2 主内点法
以下のように、主問題 ($\ref{4.2}$) に対しバリア関数を用いて定義される凸最適化問題を解きつつ、$\nu→+0$ として最適解に迫る手法。
\begin{array}
&\min &\boldsymbol{c}^T\boldsymbol{x}-\nu\sum_{j=1}^{n}\log x_j \\
s.t. &A\boldsymbol{x}=\boldsymbol{b} \\
&\boldsymbol{x}>\boldsymbol{0}
\end{array}
上記の問題は $\boldsymbol{x}>\boldsymbol{0}$ を明に考えなくてよいので、等式制約のみの問題として扱える。ラグランジュ乗数法を使えば、無制約の最適化問題となるので、ニュートン法で解ける。
4.4.3 主双対内点法
主問題 ($\ref{4.2}$) および双対問題 ($\ref{4.11}$) の最適性条件に正のパラメータ $\nu$ を導入した以下の方程式を解きつつ、$\nu→+0$ として最適解に迫る方法。
\begin{array}
~A^T\boldsymbol{y}+\boldsymbol{s}=\boldsymbol{c} \\
x_js_j=\nu,~~~~j=1,\cdots,n \\
\boldsymbol{x}>\boldsymbol{0},~~\boldsymbol{s}>\boldsymbol{0}
\end{array} \tag{4-3} \label{4.37}
$k$ 回目の反復における点 $\left(\boldsymbol{x}_k,\boldsymbol{y}_k,\boldsymbol{s}_k\right)$ に対する双対性ギャップの尺度 $\rho_k$ を以下のとおり定義。
\rho_k=\frac{\boldsymbol{x}_k^T\boldsymbol{s}_k}{n}
$k$ 回目の反復における点が中心曲線上にあれば $\rho_k=\nu$ だが、実際は中心曲線上とは限らないため、$\rho_k$ は $\nu$ の近似値的な役割を果たす。中心曲線を $\nu$ が減少する方向に辿りたいため、次の点における $\nu$ の目標値 $\nu_{k+1}$ を以下のとおり定める ($0\leq\gamma<1$)。
\nu_{k+1}=\gamma\rho_k
そして、式 ($\ref{4.37}$) で $k+1$ 回目の点について、$\nu=\nu_{k+1}$ とおいた次の方程式の解 $(\Delta\boldsymbol{x}$,$\Delta\boldsymbol{y}$,$\Delta\boldsymbol{s})$ を探索方向とする。
\begin{bmatrix}
A & O & O \\
O & A^T & I \\
\rm{diag} (\boldsymbol{s}_k) & O & \rm{diag} (\boldsymbol{x}_k)
\end{bmatrix}
\begin{bmatrix}
\Delta\boldsymbol{x} \\
\Delta\boldsymbol{y} \\
\Delta\boldsymbol{s}
\end{bmatrix}
=-
\begin{bmatrix}
A\boldsymbol{x}_k-\boldsymbol{b} \\
A^T\boldsymbol{y}_k+\boldsymbol{s}_k-\boldsymbol{c} \\
\rm{diag} (\boldsymbol{x}_k)\boldsymbol{s}_k-\nu_{k+1}\boldsymbol{1}
\end{bmatrix}
制約条件を満たすようにステップ幅 $\alpha_k>0$ を決定し、解を更新する。
(このあたり、Qiitaのインライン数式がバグって数式がうまく書けなかったです。)
4.5 凸2次計画問題とその解法
凸2次計画問題とは、目的関数が凸2次関数で制約がすべて線形な以下のような問題。なお、$Q$ は半正定値対称行列。
\begin{array}
&\min &\frac{1}{2}\boldsymbol{x}^TQ\boldsymbol{x}+\boldsymbol{c}^T\boldsymbol{x} \\
s.t. &A\boldsymbol{x}\geq\boldsymbol{b}
\end{array}
双対問題は以下。
\begin{array}
&\max &-\frac{1}{2}\boldsymbol{x}^TQ\boldsymbol{x}+\boldsymbol{b}^T\boldsymbol{y} \\
s.t. &A^T\boldsymbol{y}-Q\boldsymbol{x}=\boldsymbol{c} \\
&\boldsymbol{y}\geq\boldsymbol{0}
\end{array}
凸2次計画問題は弱双対性・強双対性を持つ。
$\boldsymbol{x}$ および $(\boldsymbol{y},\boldsymbol{x})$ が最適解であるための必要十分条件は以下。
\begin{array}
&A^T\boldsymbol{y}-Q\boldsymbol{x}=\boldsymbol{c} \\
A\boldsymbol{x}-\boldsymbol{b}\geq\boldsymbol{0} \\
\boldsymbol{y}\geq\boldsymbol{0} \\
y_j(A\boldsymbol{x}-\boldsymbol{b})_j=0,~~~~~j=1,\cdots,n
\end{array}
一般の凸2次計画問題の解法としては、内点法が1番有効。線形計画問題と同様にして主双対内点法を設計することができる。
しかし、問題の特殊な構造を活かすことにより、有効制約法と呼ばれる手法を利用してより効率的な方法を構築できる余地がある。有効制約法とは、現在得られている実行可能解において有効な不等式制約のみを取り出して等式制約つき最適化問題を解き、その解がKKT条件を満たしているかチェックする方法。アルゴリズムは以下。
0. $k$ 回目の反復で最適解を得られた場合の有効制約の集合を以下で定義する。
I^k=\lbrace i~|~\boldsymbol{a}_i^T\boldsymbol{x}^k=\boldsymbol{b}_i \rbrace
このとき、相補性条件より $i\notin I^k$ のとき $y_i=0$ だから、以下が成り立つ。有効制約に対応する制約を並べた行列を $\tilde{A}^k$、有効制約に対応する $\boldsymbol{y}$ の成分だけを取り出したベクトルを $\tilde{\boldsymbol{y}}^k$ と書いている。
A^T\boldsymbol{y}^k-Q\boldsymbol{x}^k-\boldsymbol{c}={\tilde{A}^k}^T\tilde{\boldsymbol{y}}_i^k-Q\boldsymbol{x}^k-\boldsymbol{c}=0
さらに有効制約では等式が成り立つ条件も加えると、以下のように書ける。有効制約に対応する $\boldsymbol{b}$ の成分だけを取り出したベクトルを $\tilde{\boldsymbol{b}}$ と書いている。
\begin{bmatrix}
-Q & {\tilde{A}^k}^T \\
{\tilde{A}^k}^T & O
\end{bmatrix}
\begin{bmatrix}
\boldsymbol{x}^k \\
\tilde{\boldsymbol{y}}^k
\end{bmatrix}
=
\begin{bmatrix}
\boldsymbol{c} \\
\tilde{\boldsymbol{b}}^k
\end{bmatrix} \tag{4-4} \label{validConstraintMethod}
- 実行可能解 $\boldsymbol{x}^0$ が得られたとし、$k=0$、$W^0=I^0$ とする。。
- ($\ref{validConstraintMethod}$) を解き、その解を $(\hat{\boldsymbol{x}}^k, \hat{\boldsymbol{y}}^k)$ とする。$\hat{\boldsymbol{x}}^k=\boldsymbol{x}^k$ なら4.へ進む。
- ステップ幅 $\alpha^k$ を適当に決定し、$\boldsymbol{x}^{k+1}=\boldsymbol{x}^k+\alpha(\hat{\boldsymbol{x}}^k-\boldsymbol{x}^k)$ とする。新たに有効になった解があればそれを $W^k$ に加えて $W^{k+1}$ とする。$k=k+1$ として1.へ戻る。
- $\hat{\boldsymbol{y}}^k\geq\boldsymbol{0}$ なら終了し、$\boldsymbol{x}^k$ を最適解として出力。そうでない場合は、以下の更新をして1.に戻る。
\begin{array}
\hat{y}_t^k = \min_{i\in I^k}\hat{y}_i^k \\
W^k=W^k-\lbrace t\rbrace
\end{array}
5. 半正定値計画
5.1 半正定値計画問題
対称行列 $X\in S^n$ を変数とする以下のような最適化問題。変数がベクトルではなく対称行列である点、その半正定値性を制約として含むことが特徴。
\begin{array}
&\displaystyle\min_{X\in S^n} &C\cdot X \\
s.t. &A_i\cdot X=b_i, &i=1,\cdots,m \\
&X\succeq O
\end{array}
双対問題は以下。双対問題もまた半正定値計画問題であり、適当な変換を施すことで主問題と同様の形式に変換することができる。
\begin{array}
&\max &\displaystyle\sum_{i=1}^{m}b_iy_i \\
s.t. &\displaystyle\sum_{i=1}^{m}y_iA_i+S=C \\
&S\succeq O
\end{array}
半正定値対称行列の集合 $S_+^n$ は自己双対錐である。主問題と双対問題の形式が一致するという性質は、この自己双対性に由来する。また、比較的緩い仮定の下で、主問題と双対問題の最適値が一致するという双対性を持つ。これらは、内点法の基礎となる特徴である。
自己双対錐には、非負ベクトルの集合 $\mathbb{R}^n_+=\lbrace\boldsymbol{x}\in\mathbb{R}^n~|~\boldsymbol{x}\geq\boldsymbol{0}\rbrace$ や2次錐などが知られている。自己双対錐に関連する問題には以下のようなものがある。
- 線形計画問題:錐 $\mathbb{R}^n$ と線形の等式を制約として線形関数を最小化する問題
- 2次錐計画問題:2次錐と線形の等式を制約として線形関数を最小化する問題
なお、一般の最適化問題では、双対問題は必ずしも主問題と同じ形式の問題になるとは限らないし、双対性が成り立つとも限らない。
さまざまな問題を半正定値計画問題として定式化するのにしばしば有効なのが、Schurの補元に関する次の性質。
行列 $A, B, C$ に対して、$Z$ を以下のように定義する。$A\succeq O$ のとき、条件 $Z\succeq O$ と条件 $B-C^TA^{-1}C\succeq O$ とは同値である。
Z=
\begin{bmatrix}
A & C \\
C^T & B
\end{bmatrix}
上記の性質を用いて凸2次計画や凸2次制約を含む問題を半正定値計画に変換することが可能。例えば以下。$\displaystyle t \geq \frac{1}{2}\boldsymbol{x}^T Q\boldsymbol{x}+\boldsymbol{c}^T\boldsymbol{x}$ を線形行列不等式に置き換えている。ただし、$LL^T = Q$。
\begin{array}
&\min &\displaystyle\frac{1}{2}\boldsymbol{x}^T Q\boldsymbol{x}+\boldsymbol{c}^T\boldsymbol{x} \\
s.t. &A\boldsymbol{x}\leq\boldsymbol{b}
\end{array}
\iff
\begin{array}
&\min &t \\
s.t. &\begin{bmatrix}
\displaystyle\frac{1}{2}I & L^T\boldsymbol{x} \\
\boldsymbol{x}^T L & -\boldsymbol{c}^T\boldsymbol{x}-t
\end{bmatrix}
\succeq O \\
&A\boldsymbol{x}\leq\boldsymbol{b}
\end{array}
以下のS補題はFarkasの補題の2次不等式への拡張とも言える重要な命題。
$A, B\in S^n$ を定行列とし、条件 $\hat{\boldsymbol{y}}^T A\hat{\boldsymbol{y}}>0$ を満たす $\hat{\boldsymbol{y}}\in\mathbb{R}^n$ が存在することを仮定すると、以下の2つの条件は同値である。
(a) $B-\tau A\succeq O,~\tau\geq 0$ を満たす $\tau\in\mathbb{R}$ が存在する。
(b) $\boldsymbol{y}^T A\boldsymbol{y}\geq 0$ を満たす任意の $\boldsymbol{y}$ に対して $\boldsymbol{y}^T B\boldsymbol{y}\geq 0$ が成立する。
5.2 双対性と内点法
5.2.1 双対定理
以下のとおり弱双対性が成り立つ。
\displaystyle C\cdot X-\boldsymbol{b}^T\boldsymbol{y}=\left(\sum_{i=1}^{m}y_iA_i+S\right)\cdot X-\sum_{i=1}^{m}\left(A_i\cdot X\right)y_i=X\cdot S\geq 0
また、以下のとおり強双対性が成り立つ。
- 主問題と双対問題の両方に、内点実行可能解が存在することを仮定する。このとき、それぞれの問題に最適解が存在する。また、実行可能解 $X$ および $(\boldsymbol{y}, S)$ がそれぞれの問題の最適解であるための必要十分条件は、主問題と双対問題の目的関数値が一致すること、すなわち $X\cdot S=0$ である。
主問題と双対問題に内点実行可能解が存在するとき、最適解の必要十分条件は以下。
\begin{array}
~A_i\cdot X=b_i,~~~~~i=1,\cdots,m \\
\displaystyle\sum_{i=1}^{m}y_iA_i+S=C \\
XS=O \\
X\succeq O,~~S\succeq O
\end{array}
線形計画問題を最適性条件を行列に拡張したような形。3つ目と4つ目の条件は、直交行列 $Q$ を用いて固有値分解できて、固有値 $\lambda_j$ および $\omega_j$ が以下を満たすことと同値。
\lambda_j\geq 0,~~~~\omega_j\geq 0,~~~~\lambda_j\omega_j=0,~~~~~j=1,\cdots,n
5.2.2 半正定値計画問題のスケーリング
半正定値計画問題は、正則行列 $P\in\mathbb{R}^{n\times n}$ を1つ固定して線形変換を行っても等価な問題となる。
\tilde{X}=P^{-1} X{P^{-1}}^T,~~\tilde{A}_i=P^T A_iP,~~\tilde{\boldsymbol{y}}=\boldsymbol{y},~~\tilde{S}=P^T SP
5.2.3 半正定値計画問題の内点法
半正定値計画問題の代表的な解法は内点法。主内点法や主双対内点法があり、特に主双対内点法は実用も多い重要な解法。
バリア関数を $X$ の行列式に対して定義して、以下のような最適化問題を考える。
\begin{array}
&\displaystyle\min_{X\in S^n} &C\cdot X-\nu\log (\det X) \\
s.t. &A_i\cdot X=b_i, &i=1,\cdot,m \\
&X\succeq O
\end{array}
双対問題に対しても同様に、バリア関数を付加した最適化問題を考える。
\begin{array}
&\max &\displaystyle\sum_{i=1}^{m}b_iy_i+\nu\log (\det S) \\
s.t. &\displaystyle\sum_{i=1}^{m}y_iA_i+S=C \\
&S\succeq O
\end{array}
これらの最適性条件は以下。
\begin{array}
~A_i\cdot X=b_i,~~~~~i=1,\cdots,m \\
\displaystyle\sum_{i=1}^{m}y_iA_i +S=C \\
XS=\nu I \\
X\succeq O,~~S\succeq O
\end{array} \tag{5-1} \label{5.24}
初期点を $(X_0,\boldsymbol{y}_0,S_0)$ とし、順次以下の式に従って解を更新する。
\begin{array}
~X_{k+1}=X_k+\alpha_k\Delta X \\
\boldsymbol{y}_{k+1}=\boldsymbol{y}_k+\alpha_k\Delta\boldsymbol{y} \\
S_{k+1}=S_k+\alpha_k\Delta S
\end{array}
$k$ 回目の反復で得られている点 $ (X_k,\boldsymbol{y}_k,S_k) $ に対する双対性ギャップの尺度 $\rho_k$ を以下のとおり定義する。中心曲線上では $\rho_k=\nu$。
\displaystyle\rho_k = \frac{X_k\cdot S_k}{n}
$k+1$ 回目の点における $\nu_{k+1}$ の目標値を定数 $\gamma\in (0,1)$ を用いて以下のとおり定める。
\nu_{k+1}=\gamma\rho_k
式 ($\ref{5.24}$) で $\nu=\nu_{k+1}$ とおいた式を線形近似して解き、探索方向 $(\Delta X,\Delta\boldsymbol{y},\Delta S)$ とし、適当なステップ幅 $\alpha_k$ を定めて次の点に移る。
なお、式 ($\ref{5.24}$) で $\nu=\nu_{k+1}$ とおき線形近似した方程式は、式の本数が変数の数より多いため、解をもつとは限らないという問題点がある。解決策として、3本目の式を以下のように緩和する方法がある。
XS+SX=2\nu I
5.4 2次錐計画
5.4.1 2次錐計画問題
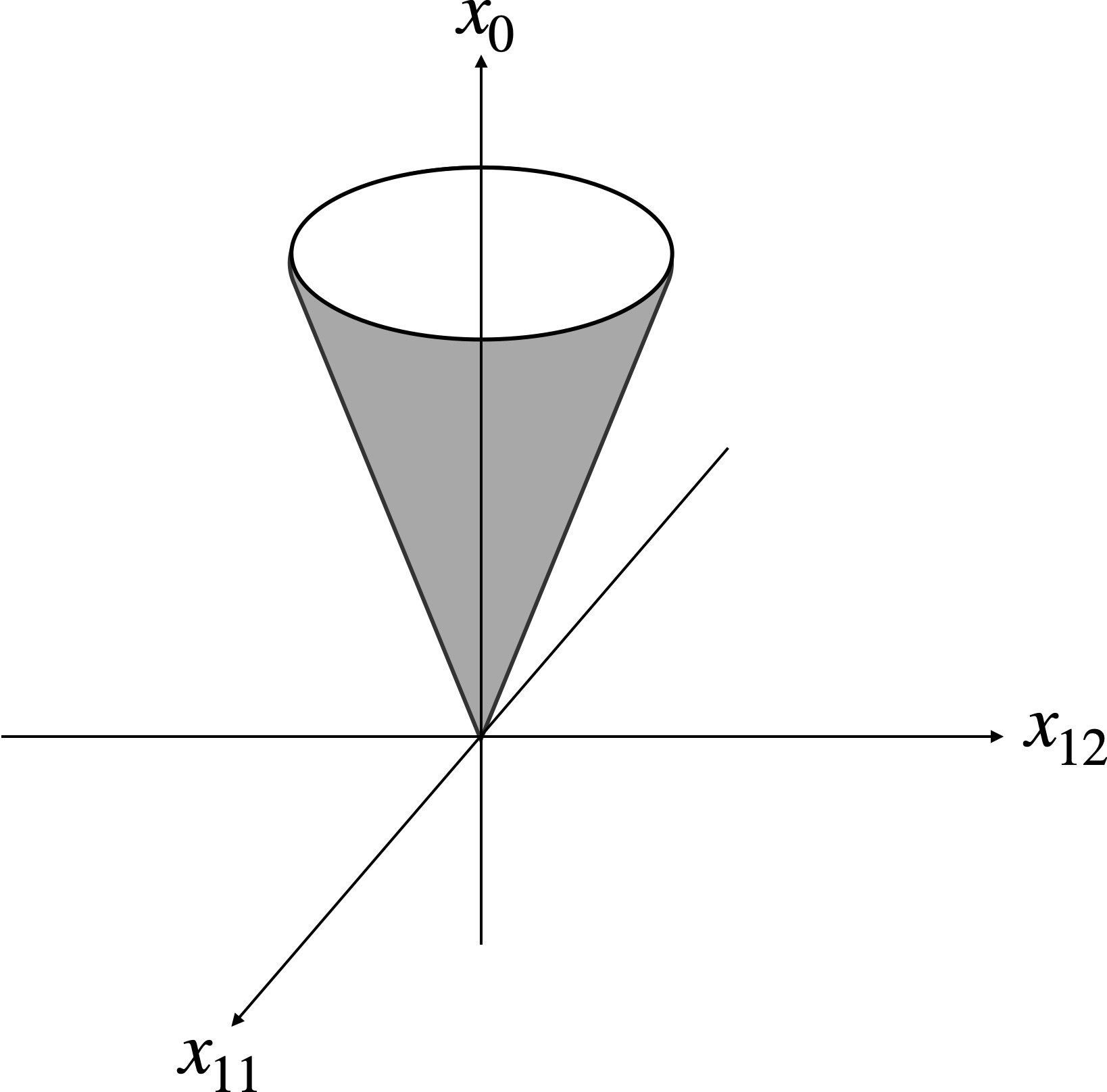
スカラー $x_0$ とベクトル $\boldsymbol{x}_1\in\mathbb{R}^{n-1}$ に対して定義される以下の集合を $n$ 次元の2次錐と呼ぶ。
L^n=\lbrace\left(x_0,\boldsymbol{x}_1\right)~|~\boldsymbol{x}\geq\|\boldsymbol{x}_1\|\rbrace
$n=3$ のときの2次錐は以下のイメージ。
条件 $\boldsymbol{x}\in L^n$ を2次錐制約と呼び、いくつかの2次錐制約と線形の等式制約の下で線形の目的関数を最小化する最適化問題を、2次錐計画問題と呼ぶ。
\begin{array}
&\min &\displaystyle\sum_{l=1}^{r}\boldsymbol{c}_l^T\boldsymbol{x}_l \\
s.t. &\displaystyle\sum_{l=1}^{r}A_l\boldsymbol{x}_l=\boldsymbol{b} \\
&x_{l0}\geq\|\boldsymbol{x}_{l1}\|, &l=1,\cdots,r
\end{array}
双対問題は以下。双対問題も2次錐計画問題。2次錐計画問題は半正定値計画問題なので当然。弱双対性・強双対性も成り立つ。
\begin{array}
&\max &\boldsymbol{b}^T\boldsymbol{y} \\
s.t. &A_l^T\boldsymbol{y}+\boldsymbol{s}_l=\boldsymbol{c}_l, &l=1,\cdots,r \\
&s_{l0}\geq\|\boldsymbol{s}_{l1}\|, &l=1,\cdots,r
\end{array}
最適性条件は以下。
\begin{array}
~\displaystyle\sum_{l=1}^{r}A_l\boldsymbol{x}_l=\boldsymbol{b} \\
A_l^T\boldsymbol{y}+\boldsymbol{s}_l=\boldsymbol{c}_l,~~~~~l=1,\cdots,r \\
x_{l0}s_{l0}+\boldsymbol{x}_{l1}^T\boldsymbol{s}_{l1}=0,~~~~~l=1,\cdots,r \\
x_{l0}\geq\|\boldsymbol{x}_{l1}\|,~~~s_{l0}\geq\|\boldsymbol{s}_{l1}\|,~~~~~l=1,\cdots,r
\end{array}
相補性条件を書き下すと以下。2次錐制約のうちいずれか一方が非有効であればもう一方の変数はゼロベクトルになることを表している。
\begin{array}
&x_{l0}>\|\boldsymbol{x}_{l1}\|, &\left(s_{l0},\boldsymbol{s}_{l1}\right)=\left(0,\boldsymbol{0}\right) \\
\left(x_{l0},\boldsymbol{x}_{l1}\right)=\left(0,\boldsymbol{0}\right), &s_{l0}>\|\boldsymbol{s}_{l1}\| \\
x_{l0}=\|\boldsymbol{x}_{l1}\|, &s_{l0}=\|\boldsymbol{s}_{l1}\|, &\|x_{l1}\|\|\boldsymbol{s}_{l1}\|+\boldsymbol{x}_{l1}^T\boldsymbol{s}_{l1}=0
\end{array}
5.4.2 2次錐計画問題の解法
内点法。特に主双対内点法。
主問題にバリア関数を組み込んだ以下の最適化問題を考える。
\begin{array}
&\min &\displaystyle\sum_{l=1}^{r}\boldsymbol{c}_l^T\boldsymbol{x}_l-\frac{\nu}{2}\sum_{l=1}^{r}\log\left(x_{l0}^2-\|\boldsymbol{x}_{l1}\|^2\right) \\
s.t. &\displaystyle\sum_{l=1}^{r}A_l\boldsymbol{x}_l=\boldsymbol{b} \\
&x_{l0}>\|\boldsymbol{x}_{l1}\|, &l=1,\cdots,r
\end{array}
この問題の最適性条件は以下。
\begin{array}
~\displaystyle\sum_{l=1}^{r}A_l\boldsymbol{x}_l=\boldsymbol{b} \\
A_l^T\boldsymbol{y}+\boldsymbol{s}_l=\boldsymbol{c}_l,~~~~~l=1,\cdots,r \\
\begin{bmatrix}
x_{l0}s_{l0}+\boldsymbol{x}_{l1}^T\boldsymbol{s}_{l1} \\
s_{l0}\boldsymbol{x}_{l1}+x_{l0}\boldsymbol{s}_{l1}
\end{bmatrix}
=\nu\begin{bmatrix}
1 \\
\boldsymbol{0}
\end{bmatrix}
,~~~~~l=1,\cdots,r \\
x_{l0}>\|\boldsymbol{x}_{l1}\|,~~~s_{l0}>\|\boldsymbol{s}_{l1}\|,~~~~~l=1,\cdots,r
\end{array}
上記方程式を解いて探索方向を決定して、解を更新する。今までの主双対内点法と一緒なので省略。
6. 組合せ最適化問題の複雑さ・難しさ
さまざまな問題に対して、効率的なアルゴリズムの存否や問題の難易度の意味といった観点から、問題の難しさや複雑さを研究するのが計算複雑性理論。
6.1 アルゴリズムの計算量
- 時間計算量:アルゴリズムが停止するまでに必要な四則演算などの基本操作の実行回数を表す。
- 空間計算量:アルゴリズムが停止するまでに必要なメモリ量を表す。
6.2 計算量とアルゴリズムの分類
- 多項式時間アルゴリズム:計算量が多項式で書ける場合。
- 指数時間アルゴリズム:計算量が多項式関数では抑えられない場合。
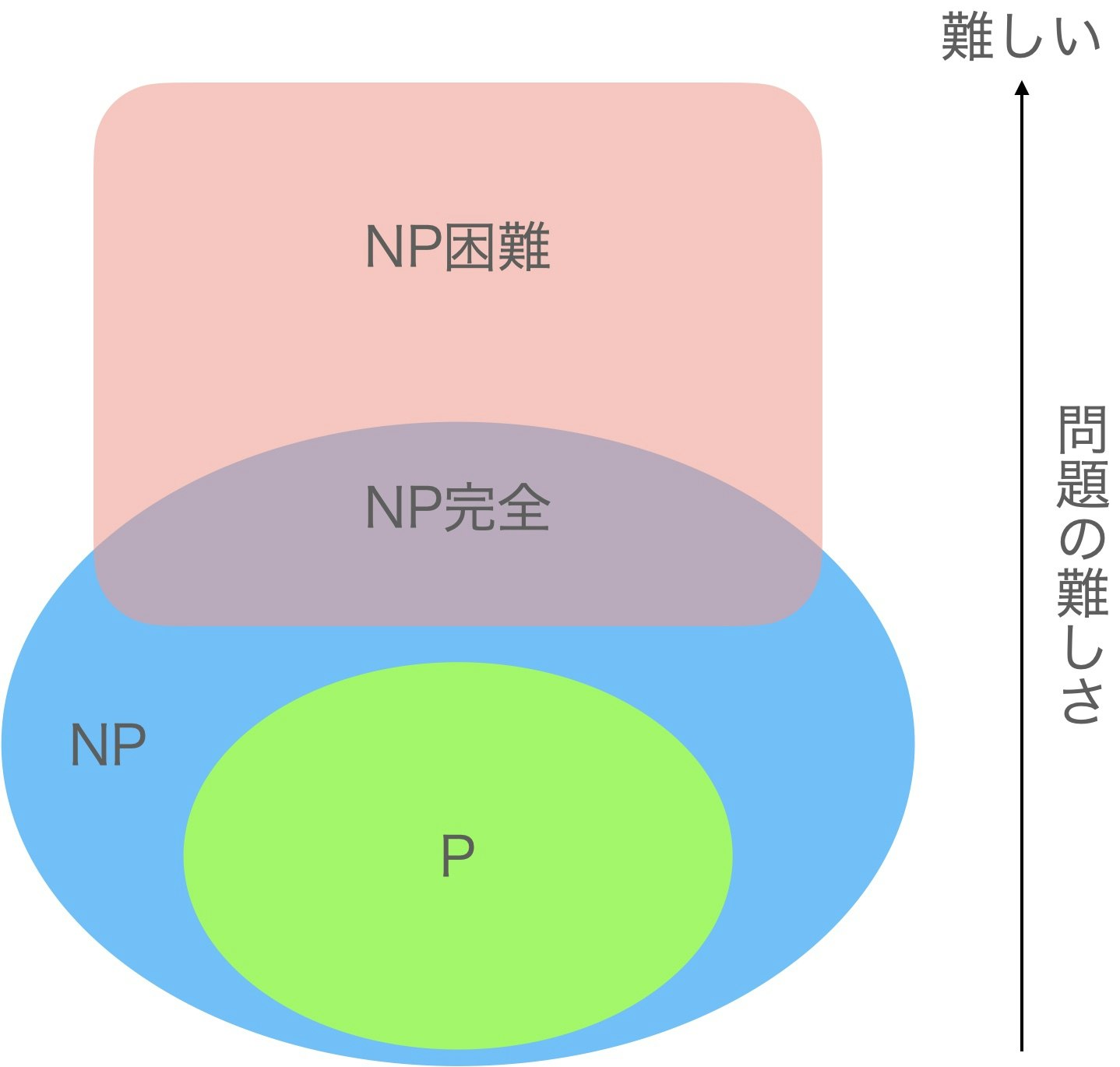
6.3 計算の複雑さと問題の難しさ
- クラス $P$:決定性のコンピュータ (分岐を並列に同時に実行可能なコンピュータ) で多項式時間で解ける問題の集合。
- クラス $NP$:非決定性のコンピュータ (分岐を並列に同時に実行可能なコンピュータ) で多項式時間で解ける問題の集合。
- $NP$ 困難:クラス $NP$ に含まれる任意の問題と難しさが同等かそれ以上の問題の集合。
- $NP$ 完全:クラス $NP$ に属する問題のうち、$NP$ 困難な問題クラス。
これらの複雑性クラスについて以下のような話題がある。
- $P\subseteq NP$ である。
- $P\neq NP$ であるかは分かっていない ($P\neq NP$ 予想)。
- $NP$ 困難な問題に対して、多項式時間アルゴリズムが存在しないことは証明されていない。
6.4 複雑性クラスと組合せ最適化問題
各組合せ最適化問題の複雑性クラスは以下。
- クラス $P$:オイラー閉路問題、最短路問題、最大流問題、最小費用流問題、最小全域木問題、割当問題、2-SAT、最大マッチング問題、最大重みマッチング問題、最大重み最大マッチング問題
- $NP$ 困難:整数最適化問題、巡回セールスマン問題、最大安定集合問題、集合分割問題、ナップザック問題、ビンパッキング問題、最大クリーク問題、最小頂点被覆問題、最小極大マッチング問題
7. 組合せ最適化問題の全体像
以下の図のように整理される。

8. 組合せ最適化の標準問題
8.1 グラフ問題・ネットワーク問題
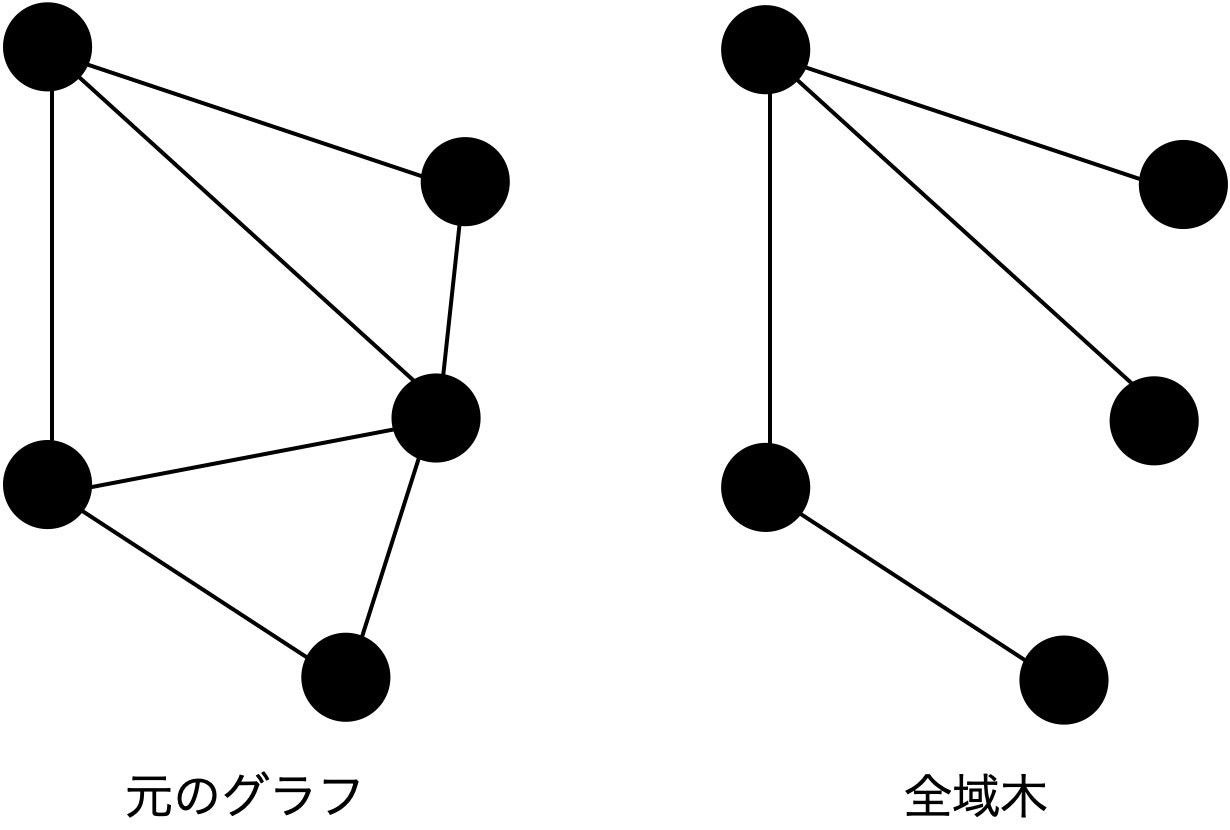
8.1.1 最小全域木問題
問題
最小全域木とは、当該グラフの全ノードを含む部分グラフのうち、連結で閉路を持たないグラフ (=木) のこと。
無向グラフ $G=(V, E)$ 上の辺 $e$ の重みを $w(e)$ とするとき、全域木 $T=(V, E_T)$ 上の辺の重みの総和 $\displaystyle\sum_{e\in E_T}w(e)$ を最小にする全域木を求める問題。
定式化は以下。$\delta (S)$ は、$S\subset V$ に一方の端点、$V\setminus S$ にもう一方の端点を持つ辺全体の集合。
\begin{array}
&\min &\displaystyle\sum_{e\in E}w(e)x_e \\
s.t. &\displaystyle\sum_{e\in C}x_e\leq |C|-1 &\forall C: \rm{closed~path~of}~G \\
&\displaystyle\sum_{e\in\delta (S)}x_e\geq 1 &\forall S\subset V,~S\neq\emptyset,~S\neq V \\
&x_e\in\lbrace 0,1\rbrace &\forall e\in E
\end{array}
制約条件は、木であることの必要十分条件。定式化にはいくつかバリエーションがある。
データのクラスター分析やネットワークの設計に使われる。
解法
クラスカル法やプリム法などの貪欲法ベースの多項式時間アルゴリズムがある。
クラスカル法は以下。if文の判定には、Union-Find木を使うと効率的。計算量は $O(|E|\log |V|)$。
T ← 空グラフ
E ← すべての辺の集合
while (E が空でない)
e ← 重みが最小の辺
E から e を削除する
if (e の端点のうち少ないとも一方が T に含まれない)
T ← T + e
end if
end while
プリム法は以下。重み最小のエッジ選択にはヒープを使うと速い。計算量はヒープを使う場合で $O(|E|\log |V|)$。
T ← 適当に選んだノード1つのみの集合
V ← すべての頂点の集合
while (V が空でない)
e ← T に含まれるノードを始点、含まれないノードを終点とするエッジのうち、重み最小のもの
E から e を削除する
T ← T + e
end while
8.1.2 最大カット問題
問題
カットとは、無向グラフ $G=(V,E)$ において、$V$ を2つの部分集合 $V_1, V_2$ に分割する組合せのこと。
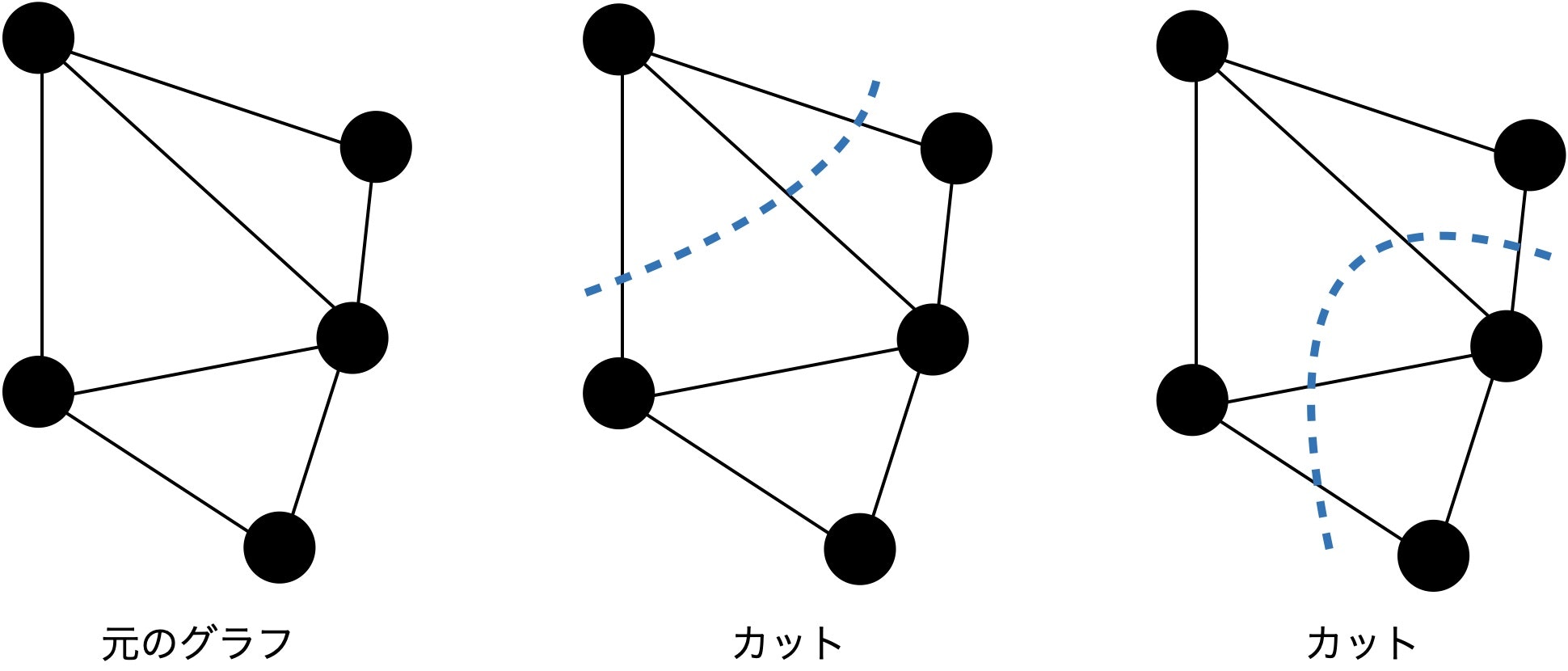
無向グラフ $G=(V,E)$ において、$\displaystyle\sum_{v_i\in V_1, v_j\in V_2, i<j}w_{ij}$ を最大にするカット $V_1, V_2$ を求める問題。
定式化は以下。$u_i\in\lbrace -1,1\rbrace$ は、ノード $i$ が $V_1$ に属する場合 $+1$、$V_2$ に属する場合 $-1$ を割り当てる。
\begin{array}
&\max &\displaystyle\frac{1}{2}\sum_{v_i\in V_1,v_j\in V_2, i<j}w_{ij}(1-u_iu_j) \\
s.t. &u_i\in\lbrace -1,1\rbrace &\forall v_i\in V
\end{array}
ネットワーク監視の効率化などに用いられる。より複雑な組合せ最適化問題の部分問題として用いられることも多い。
解法
NP完全。メタヒューで解く。多項式時間アルゴリズムは存在しないと考えられている。
なお、最小カット問題には多項式時間アルゴリズムが存在する。最小カット問題は最大流問題の双対問題。
8.1.3 最小頂点被覆問題
問題
頂点被覆とは、頂点の集合 $C\subseteq V$ であり、任意のエッジについて少なくとも一方の端点が $C$ に含まれるもの。
頂点被覆 $C$ のうち要素数 $|C|$ が最小のものを求める問題。
重みつきの場合の定式化は以下。
\begin{array}
&\min &\displaystyle\sum_{v_i\in V}w(v_i)x_i \\
s.t. &x_i+x_j\geq 1 &\forall e_{ij}=(v_i,v_j)\in E \\
&x_i\in\lbrace 0,1\rbrace &\forall v_i\in V
\end{array}
配置計画 (交差点への警備員の配置など) に用いられることが多い。より複雑な組合せ最適化問題の部分問題として用いられることも多い。
解法
NP困難。メタヒューを使うことが多い。
8.1.4 最大安定集合問題
問題
安定集合 (独立集合) とは、ノード集合 $S\subseteq V$ で $S$ の任意の2つのノードをつなぐエッジが存在しない集合のこと。
安定集合 $S$ のうち要素数 $|S|$ が最大のものを求める問題。
\begin{array}
&\max &\displaystyle\sum_{v_i\in V}x_i \\
s.t. &x_i+x_j\leq 1 &\forall e_{ij}=(v_i,v_j)\in E \\
&x_i\in\lbrace 0,1\rbrace &\forall v_i\in V
\end{array}
より複雑な組合せ最適化問題の部分問題としてしばしば用いられる。
解法
NP困難。メタヒューを使う。
8.1.5 最短路問題
問題
あるノード $v_s\in V$ から別のノード $v_t \in V$ への経路の中で最もコストの小さいものを求める問題。
エッジ $e_{ij}$ の重みを $a_{ij}$ として、定式化は以下。
\begin{array}
&\min &\displaystyle\sum_{e_{ij}\in E}a_{ij}x_{ij} \\
s.t. &\displaystyle\sum_{v_j\in V}x_{ij}-\sum_{v_k\in V}x_{ki}=\left\{
\begin{array}
~1 &i=s \\
-1 &i=t \\
0 &\rm{otherwise}
\end{array} \right. \\
&x_{ij}\in\lbrace 0,1\rbrace &e_{ij}\in E
\end{array}
鉄道の経路案内や車のナビに応用されている。
解法
単一始点最短路問題の解法は、コストが非負の場合ダイクストラ法、負のコストも許す場合ベルマン・フォード法。全点対最短路問題はワーシャル・フロイド法。
ダイクストラ法は以下。d[u] が最小となるノードの取り出しは Q にヒープを使うと効率的。計算量は $O((|E|+|V|)\log |V|)$。
すべての v について d[v] ← ∞
d[v_s] ← 0
Q ← すべての頂点の集合
while (Q が空でない)
u ← Q のうち d[u] が最小となるノード
Q から u を削除する
for each (u を始点とする辺の終点 v)
if d[v] > d[u] + cost[u, v]
d[v] ← d[u] + cost[u, v]
end if
end for
end while
ベルマン・フォード法は以下。計算量は $O(|V||E|)$。
すべての v について d[v] ← ∞
d[v_s] ← 0
for i = 1 to |V|
for each (u, v) in V
if d[v] > d[u] + cost[u, v]
d[v] = d[u] + cost[u, v]
end if
end for
end for
ワーシャル・フロイド法は以下。計算量は $O(V^3)$。
d[i, j] ← 辺 (i, j) が存在すれば cost[i, j]、存在しなければ ∞
for each k = 1 to |V|
for each i = 1 to |V|
for each j = 1 to |V|
if d[i, j] > d[i, k] + d[k, j]
d[i, j] = d[i, k] + d[k, j]
end if
end for
end for
end for
8.1.6 最大流問題
問題
容量付きのリンクから構成される有向グラフにおいて、ソースノードからシンクノードへの総流量が最大となるようなフローを求める問題。
フロー $\boldsymbol{x}$ のノード $v_i$ における超過 $f_{\boldsymbol{x}}(v_i)$ を以下のように定義する。
\displaystyle f_{\boldsymbol{x}}(v_i)=\sum_{(j,i)\in E}x_{ji}-\sum_{(i,j)\in E}x_{ij}
ソースノード $v_s$、シンクノード $v_t$、リンク $(i,j)$ の容量を $u_{ij}$ として、定式化は以下。1つ目の制約が流量保存則、2つ目の制約が容量制約。
\begin{array}
&\max &f_{\boldsymbol{x}}(v_t) \\
s.t. &f_{\boldsymbol{x}}(v_i)=0 &\forall v_i\in V\setminus\lbrace v_s,v_t\rbrace \\
&0\leq x_{ij}\leq u_{ij} &\forall e_{ij}\in E
\end{array}
水や道路交通の流れに関する問題に適用されたり、スケジューリングや分子生物学に応用されている。
解法
線形最適化問題なので単体法で解ける。
最大流問題では特に、フォード・ファルカーソン法 (フロー増加法) という効率的なアルゴリズムがある。「各リンクにフローをどれだけ追加でき、どれだけ減らすことができるか」を表す残余ネットワークという概念を導入する。
全ての e ∈ E について f[e] ← 0
while (残余ネットワークにおいてソースノードからシンクノードへのパス p が存在)
q ← パス p に含まれるエッジのうちの最小容量
パス p にフロー q を流す
end while
8.1.7 最小費用流問題
問題
有向グラフ $G=(V, E)$ において、各エッジの要領とコスト、ノードの需給量が与えられたとき、各エッジの容量を超過せず各ノードの流出量が需給量と等しくなるフローの中で、各エッジの流量に対するコストの総和が最小となるフローを求める問題。
\begin{array}
&\min &\displaystyle\sum_{(i,j)\in E}c_{ij}x_{ij} \\
s.t. &f_{\boldsymbol{x}}(v_i)=b_i &\forall v_i\in V \\
&0\leq x_{ij}\leq u_{ij} &(i,j)\in E
\end{array}
解法
- ネットワーク単体法。単体法における基底解をエッジの集合に置き換える ($x_{ij}=1$ のとき、エッジ $(i,j)$ が有効) と全域木となり、また、全域木に対して需給制約を満たすフローは一意に定まるため、基底解と全域木は一対一対応する。そのため、単体法において実行可能基底解を順々に探索するのと同様に、全域木を次々に探索するという発想。新しい全域木 (=実行可能基底解) を求める際は、需給制約を満たしつつ新たなエッジに $\theta$ だけ流して閉路を発生させたときに、最初に流量が負となるエッジを取り除けばよい。
- 負閉路除去法。残余ネットワークにおいて、元のエッジと逆向きのエッジのコストを、元のエッジのコストの-1倍とする。
f[e] ← フロー保存条件を満たすフロー
while (負の閉路が存在)
f[e] ← 負の閉路に流せるだけ流したときのフロー
end while
8.2 経路問題
8.2.1 運搬経路問題 (Vehicle Routing Problem, VRP)
問題
デポから出発し、いくつかのノードを訪問してデポに戻るルートを最適化する。需要量や移動コスト、最大稼働時間などの制約のもとで解く。バリエーションがいくつかある。
例えば、以下の問題。
顧客の集合 $V=\lbrace 0,\cdots,n\rbrace$ と運搬車の集合 $M=\lbrace 1,\cdots,M\rbrace$ が与えられたとする。各運搬車はデポ $0$ を出発して割り当てられた顧客集合をめぐり配送を行い、デポ $0$ に戻る。各顧客 $i\in V$ についてサービスの需要量は $a_i$、各運搬車 $k\in M$ の最大積載量は $u$ であり、顧客 $i, j$ 間の移動コストが $c_{ij}$ であるとする。各顧客の需要は1台の運搬車の1度の訪問で満たされる。このとき、総移動コストが最大となるように全ての運搬車のルートを求めよ。
$x_{ij}^k$ は運搬車 $k$ が顧客 $i$ から $j$ へ進むか否かのバイナリ変数、$w_i^k$ は運搬車 $k$ が顧客 $i$ までに訪問した顧客の需要量の総和として、定式化は以下。
\begin{array}
&\min &\displaystyle\sum_{(i,j)\in E}c_{ij}\sum_{k\in M}x_{ij}^k \\
s.t. &\displaystyle\sum_{j\in\lbrace j|(0,j)\in E\rbrace} x_{0j}^k=1 &\forall k\in M \\
&\displaystyle\sum_{j\in\lbrace j|(i,j)\in E\rbrace}x_{ij}^k=\sum_{j\in\lbrace j|(j,i)\in E}x_{ji}^k &\forall i\in V, \forall k\in M \\
&w_j^k\geq a_j-u\left( 1-x_{ij}^k\right) &\forall (i,j)\in E, i=0, \forall k\in M \\
&w_j^k\geq w_i^k+a_j-u\left( 1-x_{ij}^k\right) &\forall (i,j)\in E, i\neq 0, \forall k\in M \\
&w_i^k\leq u &\forall i\in V, \forall k\in M \\
&\displaystyle\sum_{j\in\lbrace j|(i,j)\in E\rbrace}\sum_{k\in M}x_{ij}^k=1 &\forall i\in V, i\neq 0 \\
&x_{ij}^k \in \lbrace 0,1\rbrace &\forall (i,j)\in E,\forall k\in M \\
&w_i^k\geq 0 &\forall i\in V, \forall k\in M
\end{array}
店舗への配送、郵便などの配達、ごみ収集、航空機の路線決定など幅広い問題をカバーしている。
解法
バリエーションのほとんどはNP困難のため、近似解法やメタヒュー。集合被覆問題として定義されることもある。
8.2.2 巡回セールスマン問題 (Traveling Salesman Problem, TSP)
問題
すべてのエッジを1回ずつ通り最初のエッジに戻るルートのうち、総コストが最小となるルートを求める問題。
定式化は以下。
\begin{array}
&\min &\displaystyle\sum_{(i,j)\in E}c_{ij}x_{ij} \\
s.t. &\displaystyle\sum_{j=1}^{n}x_{ij}=1 &\forall i \in V \\
&\displaystyle\sum_{i=1}^{n}x_{ij}=1 &\forall j\in V \\
&\displaystyle\sum_{(i,j)\in\delta (S)}x_{ij}\geq 1 &\forall S\subset V,S\neq\emptyset,S\neq V \\
&x_{ij}\in\lbrace 0,1\rbrace &i,j\in V, i\neq j
\end{array}
配送計画問題やプリント基板へのドリル穴開け、VLCIの設計などに用いられる。
解法
NP困難。近似解法が多く開発されている。bit DPで計算量を $O(n!)$ から $O(n^22^n)$ までは落とせる。
8.3 集合被覆問題 (Set Covering Problem, SCP)
8.3.1 集合被覆・分割問題
問題
いくつかの要素からなる集合 $M$ と $M$ の部分集合族が与えられ、各部分集合にはコストが与えられているとする。
$M$ のすべての要素をカバーするようにいくつかの部分集合を選び、選んだ部分集合のコストの総和を最小にするのが集合被覆問題。
選ばれた部分集合が互いに重ならないという条件を課す場合が集合分割問題。
より具体的に数式に落とすと以下。集合 $M=\lbrace 1,\cdots,m\rbrace$ の $n$ 個の部分集合 $S_j \subseteq M$、$j\in N=\lbrace 1,\cdots,N\rbrace$ を考える。このとき、以下の条件を満たす集合の族 $\lbrace S_j~|~j\in X\rbrace$ を集合 $M$ の被覆という。
\bigcup_{j\in X}S_j=M
集合 $M$ の被覆で、さらに $S_j\cap S_k=\emptyset,~j,k\in X,~j\neq k$ が成り立つ場合、集合 $M$ の分割という。
集合被覆問題の定式化は以下。
\begin{array}
&\min &\displaystyle\sum_{j=1}^{n}c_jx_j \\
s.t. &\displaystyle\sum_{j=1}^{n}a_{ij}x_j\geq 1 &\forall i\in M \\
&x_j\in\lbrace 0,1\rbrace &\forall j\in N
\end{array}
集合分割問題の定式化は以下。
\begin{array}
&\min &\displaystyle\sum_{j=1}^{n}c_jx_j \\
s.t. &\displaystyle\sum_{j=1}^{n}a_{ij}x_j=1 &\forall i\in M \\
&x_j\in\lbrace 0,1\rbrace &\forall j\in N
\end{array}
運搬経路問題、スケジューリング問題、施設配置問題、割当問題など、別の標準問題に応用される。集合被覆問題は組合せ最適化問題において重要な基本的な問題構造であると言える。
解法
NP困難。線形緩和やラグランジュ緩和を利用した効率的な手法が提案されている。
8.4 スケジューリング問題
ジョブを様々な制約のもとで実行しなくてはならないとき、実行可能なスケジュールや最適化スケジュールを求める問題。
8.4.1 ジョブショップ問題
問題
ジョブショップとは、機械加工工場などで同種の機能や性能を持つ機械設備をグループ化して編成した機能別配置工程のこと。
ジョブショップ問題とは、ジョブごとに指定された順序で順次処理されるジョブショップにおいて、目的関数を最適にするよう書く機械におけるジョブの処理順序を決定する問題。例えば1機械問題など以下のように記述される。
与えられた $n$ 個のジョブ $V=\lbrace 1,\cdots,n\rbrace$ を1台の機械で処理するとする。各ジョブ $i$ の処理時間は $p_i$ である。機械は1度に1つのジョブしか処理できず、あるジョブの処理中は他のジョブは処理できない。また、各ジョブ $i$ には、準備時間 $r_i$ と納期 $d_i$ が与えられている。このとき、目的関数 $f$ を最小にするジョブの順列を求めよ。

$x_{ij}$ をジョブ $i$ がジョブ $j$ より先に処理されるかを表すバイナリ変数、$M$ を十分大きな数とし、定式化は以下。
\begin{array}
&\min &f \\
s.t. &c_i\geq r_i+p_i &\forall i\in V \\
&c_i\geq c_j+p_j-Mx_{ij} &\forall i,j\in V,i<j \\
&c_i\leq c_j-p_i+M(1-x_{ij}) &\forall i,j\in V,i<j \\
&c_i<d_i
\end{array}
問題のバリエーションとして、以下などがある。
- 並列機械問題:2台以上の機械で各ジョブはいずれか1台で1度だけ処理されるとき、各ジョブに対する機械の割当と各機械に割当てられたジョブの処理順序を決定する問題。
- フローショップ問題:工程順序がどのジョブについても同じ場合の問題。
- オープンショップ問題:ジョブの一部またはすべての工程順序が任意で、工程順序も最適化の対象となる場合の問題。
解法
多くのスケジューリング問題はNP困難だが、工夫された分枝限定法を持ち言えることでかなりジョブ数が大きい問題も解ける場合がある。
また、2機械の機械問題はジョンソン法という貪欲法ベースの効率的な厳密解法がある。ただし、各ジョブの準備時間と納期が全て同一であること、各ジョブには前工程と後工程の2つの処理が含まれることが条件。
while (未決定の処理が存在)
p ← 未決定かつ処理時間が最小の処理
if (p が前工程)
当該ジョブをスケジュールの最初から順に並べる
else if (p が後工程)
当該ジョブをスケジュールの後ろから順に並べる
end if
当該ジョブの各処理を決定済みとする
end while
8.4.2 勤務スケジューリング問題
問題
工場の従業員、交通機関の乗務員、病院の看護師など様々な職場におけるある期間内の勤務スケジュールを作成する問題。
看護師スケジューリング問題や乗務員スケジューリング問題など様々なバリエーションがある。例えば看護師スケジューリング問題は、以下のような条件のもとでシフトを決定する問題。
- 拘束条件1:毎日の各勤務に必要な人数確保
- 拘束条件2:スキルレベルや所属チームを考慮した各シフトの人員構成
- 拘束条件3:各看護師の勤務回数を決められた範囲内に収める
- 拘束条件4:その他の業務や休みの希望の充足
- 拘束条件5:禁止されているシフトパターンの排除
すべての制約を満たすのは難しいため、必ず守る必要のある制約は絶対制約とし、それ以外はソフト制約とすることも多い。
解法
大規模な整数計画問題なので、厳密解法は厳しい。メタヒューを適用する研究が盛ん。
8.5 切出し・詰込み問題
- 切出し問題:定型の母材から必要とされる形状や大きさの資材を切出し、母材の材料費や切出しにかかる工程費を最小化する問題
- 詰込み問題:与えられた図形をある容器の中に図形の重複がないように配置する問題
本質的には、いくつかの対象物を互いに重ならないように与えられた領域内に効率よく配置する問題。
8.5.1 ナップサック問題
問題
容量 $c$ のナップサックと $n$ 個の荷物 $N=\lbrace 1,\cdots,n\rbrace$ が与えられており、荷物 $i\in N$ の容量を $w_i$、価値を $p_i$ とするとき、容量制限 $c$ の範囲で価値の和が最大になる荷物の詰合せを求める問題。
$x_i$ を荷物 $i$ がナップサックに入っているかを表すバイナリ変数とすると、定式化は以下。
\begin{array}
&\max &\displaystyle\sum_{i=1}^{n}p_ix_i \\
s.t. &\displaystyle\sum_{i=1}^{n}w_ix_i\leq c \\
&x_i\in\lbrace 0,1\rbrace &\forall i\in N
\end{array}
解法
NP困難。厳密解法では分枝限定法や動的計画法、近似解法では局所探索法などが用いられる。動的計画法は以下。「$i$ 個目までの品物までで、ナップサックの容量が $j$ のときの最適値」をDPテーブルとする。
dp ← (N+1)×(c+1)の配列
for each j = 0 to c
dp[0][j] = 0
end for
for each i = 1 to N
for each j = 0 to c
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w_i] + p_a)
end for
end for
PRINT dp[N][C]
8.5.2 ビンパッキング問題
問題
容量 $c$ の箱と $n$ 個の荷物 $N=\lbrace 1,\cdots,n\rbrace$ が与えられており、荷物 $j\in N$ の容量を $w_j$ とするとき、すべての荷物を詰合せるのに必要な箱の数を最小にする詰合せを求める問題。
$x_{ij}$ を箱 $i$ に荷物 $j$ が入っているかのバイナリ変数、$y_i$ を箱 $i$ が使われているかのバイナリ変数とすると、定式化は以下。
\begin{array}
&\min &\displaystyle\sum_{i=1}^n y_i \\
s.t. &\displaystyle\sum_{j=1}^n w_jx_{ij}\leq cy_i &\forall i\in N \\
&\displaystyle\sum_{i=1}^n x_{ij} = 1 &\forall j \in N \\
&y_i\in\lbrace 0,1\rbrace &\forall i\in N \\
&x_{ij}\in\lbrace 0,1\rbrace &\forall i\in N, j\in N
\end{array}
解法
NP困難。分枝限定法や貪欲法・列生成法をはじめとする近似解法が用いられる。
8.5.3 その他
以下のような問題がある。
- 1次元資材切出し問題:母材から様々な大きさ位の必要とされる量の資材を切出すときに使用する母材を最小にする問題。
- 長方形詰込み問題:様々な大きさの長方形を2次元平面のある領域内に重なりのないように配置する問題。
8.6 配置問題
施設配置問題とは、施設の配置可能な候補点と施設に割当たる対象を与件とし、ある基準を満たす施設の配置を決定する問題。以下は施設配置問題の例。
- メディアン問題:顧客から最も近い施設への距離の総和を最小化するように施設を配置する問題。
- センター問題:顧客から最も近い施設への距離の最大値を最小化するように施設を配置する問題。
8.6.1 容量制約なし施設配置問題
問題
顧客の集合 $D$ と施設の配置可能地点の集合 $F$ が与えられ、各施設 $i\in F$ を開設するための固定コストを $f_i$、各顧客 $j\in D$ と各施設 $i$ の間の単位需要当たりの輸送コストを $c_{ij}$ とするとき、施設開設固定コストと輸送コストの総和が最小となるように、開設する施設を選択する問題。
$x_{ij}$ を施設 $i$ によって顧客 $j$ の需要が満たされる割合、$y_i$ を施設 $i$ を開設するか否かのバイナリ変数として、定式化は以下。MIPになる。
\begin{array}
&\min &\displaystyle\sum_{i\in F}f_iy_i+\sum_{i\in F}\sum_{j\in D}c_{ij}x_{ij} \\
s.t. &x_{ij}\leq y_i &\forall i\in F, j\in D \\
&\displaystyle\sum_{i\in F}x_{ij}=1 &\forall j\in D \\
&x_{ij}\geq 0 &\forall i\in F, j\in D \\
&y_i\in\lbrace 0,1\rbrace &\forall i\in F
\end{array}
解法
施設配置問題の多くはNP困難。緩和手法や近似手法が用いられる。
8.7 割当問題・マッチング問題
ある集合の各要素についてそれぞれ別の集合のどの要素に割当てると、さまざまな制約条件を満たしつつ、最もよい割当を行うことができるのかを決定する問題。
8.7.1 2次割当問題
問題
対象物と同数の割当先が与えられているとき、割当先間の輸送量と距離の席の総和を最小化する問題。
より具体的には、対象物 $P=\lbrace P_1,\cdots,P_n\rbrace$ の割当先 $L=\lbrace L_1,\cdots,L_n\rbrace$ を考え、対象物 $P_i$ と $P_j$ の間の輸送量 $q_{ij}$ と割当先 $L_k$ と $L_l$ の間の距離 $d_{kl}$ が与えられているとき、輸送量と距離の積の総和を最小にする割当を求める問題。
$x_{ij}$ を対象物 $P_i$ が割当先 $L_j$ に位置するか否かのバイナリ変数とし、以下のように定式化される。
\begin{array}
&\min &\displaystyle\sum_{i=1}^{n}\sum_{j=1}^{n}\sum_{k=1}^{n}\sum_{l=1}^{n}q_{ij}d_{kl}x_{ik}x_{jl} \\
s.t. &\displaystyle\sum_{j=1}^{n}x_{ij}=1 &\forall i\in V \\
&\displaystyle\sum_{i=j}^{n}x_{ij}=1 &\forall j\in V \\
&x_{ij}\in\lbrace 0,1\rbrace &\forall i,j\in V
\end{array}
工場内の機械の配置や外部記憶装置上でのデータ配列などの用途がある。
解法
NP困難。巡回セールスマン問題と同じく、目的関数を最小にする順列を求める問題だが、目的関数が2次で難しい。分枝限定法やメタヒュー。
8.7.2 一般化割当問題
問題
与えられたいくつかの仕事をエージェントに割当てるとき、割当に伴うコストの総和を最小化する問題。例えば以下。
$n$ 個の仕事 $J=\lbrace 1,\cdots,n\rbrace$ と $m$ 人のエージェント $I=\lbrace 1,\cdots,m\rbrace$ に対して、仕事 $j\in J$ をエージェント $i\in I$ に割当てたときのコスト $c_{ij}$ と資源の要求量 $a_{ij}$、および各エージェント $i\in I$ の利用可能資源量 $b_i$ が与えられている。
それぞれの仕事を必ずいずれか1つのエージェントに割当なければならず、また、各エージェントに割当てられた仕事の総資源要求量が、そのエージェントの利用可能資源量を超えないようにしなくてはならない。このとき、割当に伴うコストの総和を最小化するような割当を求めよ。
$x_{ij}$ を仕事 $j$ をエージェント $i$ に割当てるか否かのバイナリ変数として、定式化は以下。
\begin{array}
&\min &\displaystyle\sum_{i\in I}\sum_{j\in J}c_{ij}x_{ij} \\
s.t. &\displaystyle\sum_{j\in J}a_{ij}x_{ij}\leq b_i &\forall i\in I \\
&\displaystyle\sum_{i\in I}x_{ij}=1 &\forall j\in J \\
&x_{ij}\in\lbrace 0,1\rbrace &\forall i\in I,j\in J
\end{array}
解法
実行可能解が存在するかの判定問題がNP完全。一部の制約を緩和して実行不可能解も探索の対象とする方法が有効。
8.7.3 最大マッチング問題
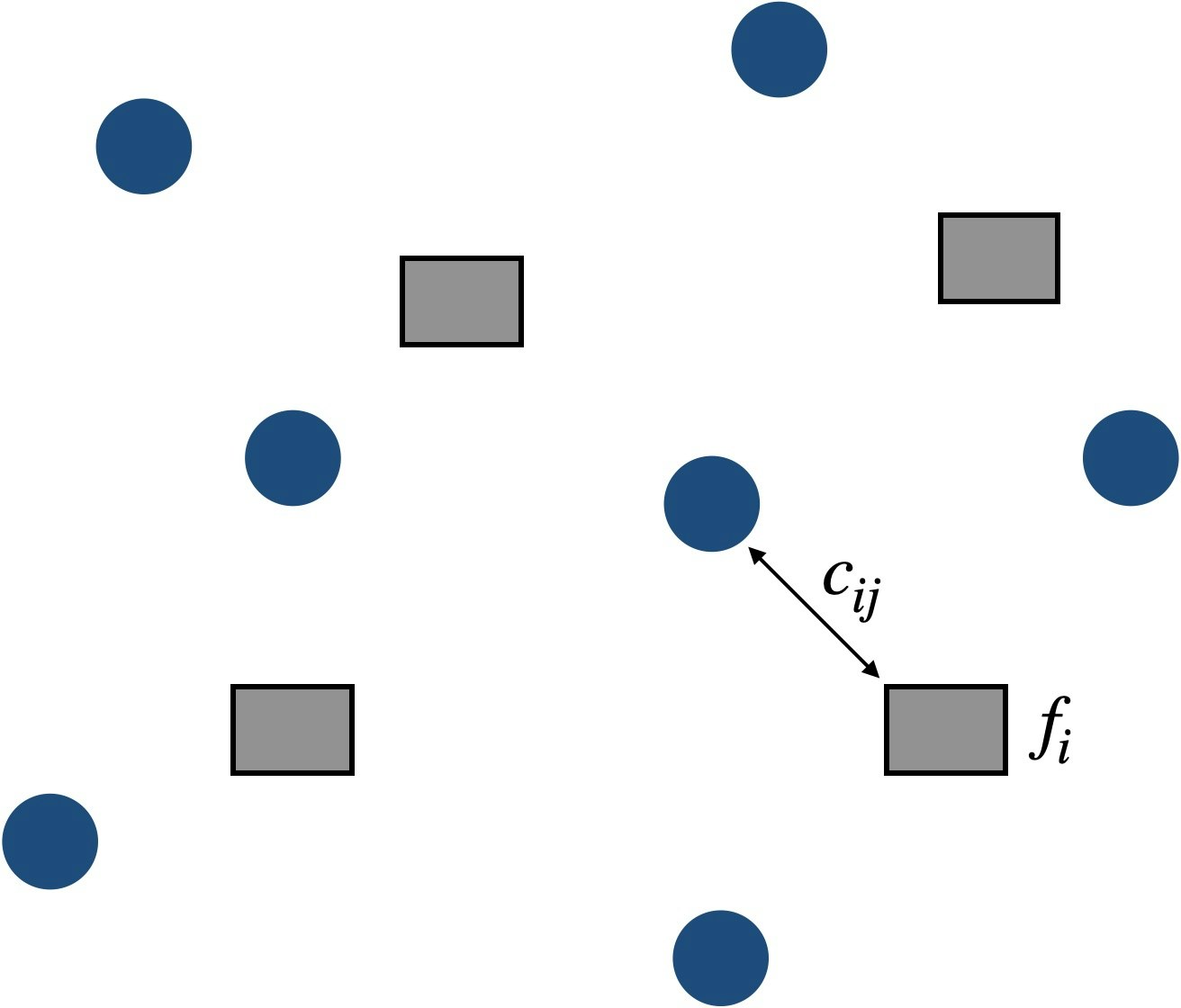
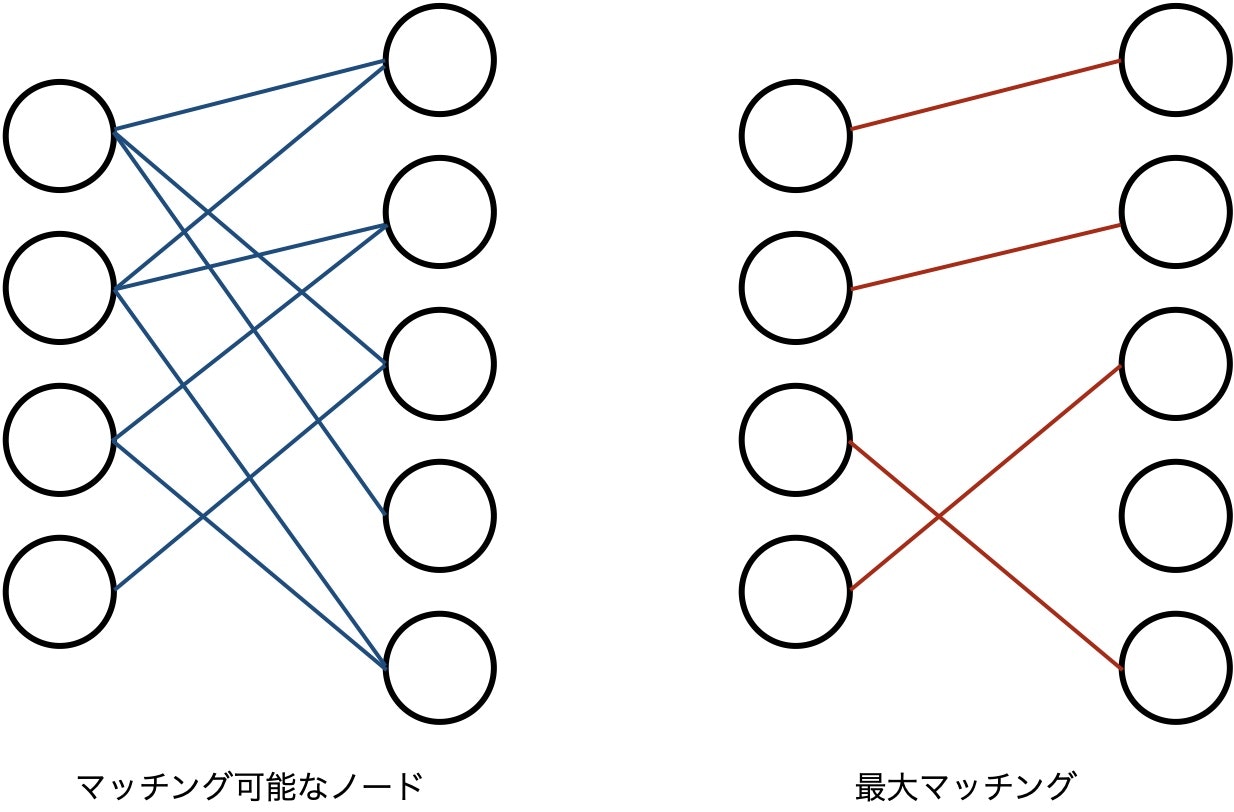
問題
無向グラフ $G=(V,E)$ に対してエッジの本数が最大のマッチングを求める問題。
$A$ を接続行列、$\boldsymbol{x}$ とエッジが存在するか否かのバイナリ変数のベクトルとして、定式化は以下。
\begin{array}
&\max &\boldsymbol{1}^T\cdot\boldsymbol{x} \\
s.t. &A\boldsymbol{x}\leq\boldsymbol{1} \\
&x(e)\in\lbrace 0,1\rbrace &\forall e\in E
\end{array}
仕事の割当や学生と授業の割り当て、人員の配属割当などに用いられる。
解法
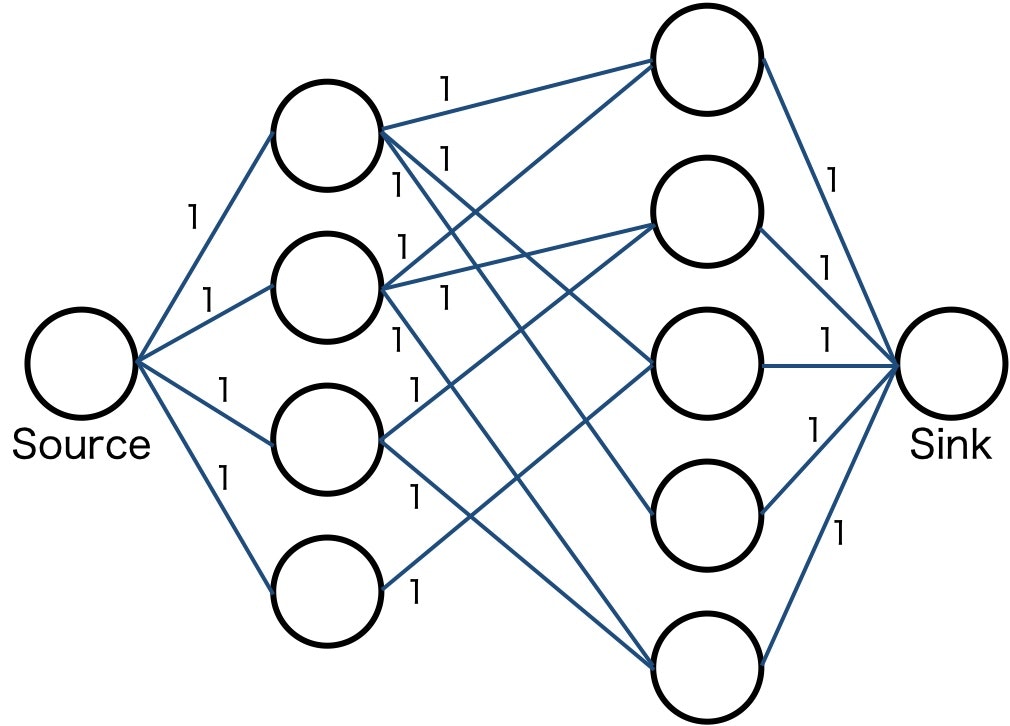
2部グラフの場合、片方のグラフに仮想的なソースノード、もう片方のグラフに仮想的なシンクノードを定義して繋ぎ、すべてのエッジの容量を1として最大流問題を考えればよい。
一般のグラフの場合はエドモンズ法 (まだ理解できていないので、理解したら追記します)。
8.7.4 最大重みマッチング問題
問題
各辺 $e\in E$ の重み $w(e)$ が与えられている無向グラフ $G=(V,E)$ に対し、重みの和 $\displaystyle\sum_{e\in M}$ が最大のマッチング $M$ を求める問題。
$\delta(v)$ をノード $v$ に接続しているエッジ集合、$x(e)$ をエッジ $e$ がマッチング $M$ の要素か否かのバイナリ変数として、定式化は以下。
\begin{array}
&\max &\displaystyle\sum_{e\in E}w(e)x(e) \\
s.t. &\displaystyle\sum_{e\in\delta(v)}x(e)\leq 1 &\forall v\in V \\
&x(e)\in\lbrace 0,1\rbrace &\forall e\in E
\end{array}
解法
2部グラフではハンガリー法。一般グラフではエドモンズ法。最大重み完全マッチングの場合のハンガリー法は以下。
for each element in A
element ← max_element - element
end for
for each row in A
element ← element - min_element_in_row
end for
for each col in A
element ← element - min_element_in_col
end for
while 値が0の成分のみで完全マッチングができない
0を含んでいる成分がなくなるように行・列を削除して行列B生成 (削除する行・列数を最小にする)
for each element in A
if element is not in 削除された行・列
element ← element - min_element_in_B
end if
end for
end while
値が0の成分のみの完全マッチングを出力
9. 解法
9.1 厳密解法
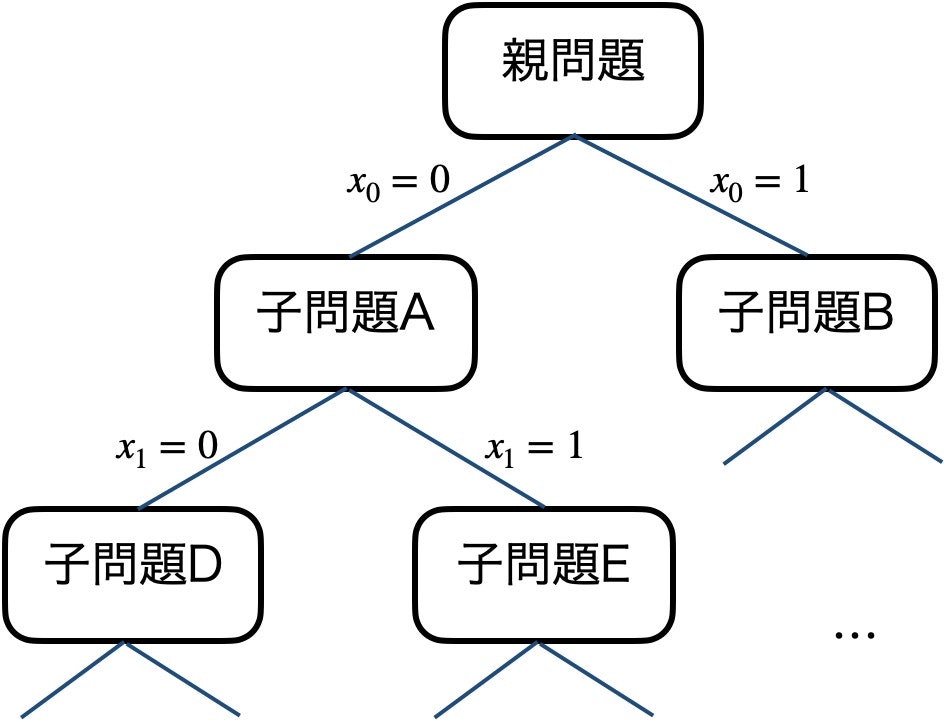
9.1.1 分枝限定法 (Branch and Bound)
変数の値で場合分けして元の問題を子問題に分割する操作と (分枝操作)、子問題以下に最適解が存在するかを確認する操作 (限定操作) とを繰り返して解を求める手法。
全探索をベースとして厳密解法だが、処理を途中で止めれば暫定解が得られる。
ナップザック問題を例にとると以下のように処理される。
- 貪欲法などで初期解を得る。初期解はこの問題の下界。
- まだ検討していない品物を選んだ場合と選ばなかった場合でそれぞれ子問題を作る (分枝操作)
- 子問題では線形緩和により解を得て、解の値が下界以下ならその子問題は切り捨てる (限定操作)。捨てない場合は子問題を再帰的に解く。いずれかの子問題で解が得られれば、下界を更新する。
- すべての子問題が解き、下界に対応する
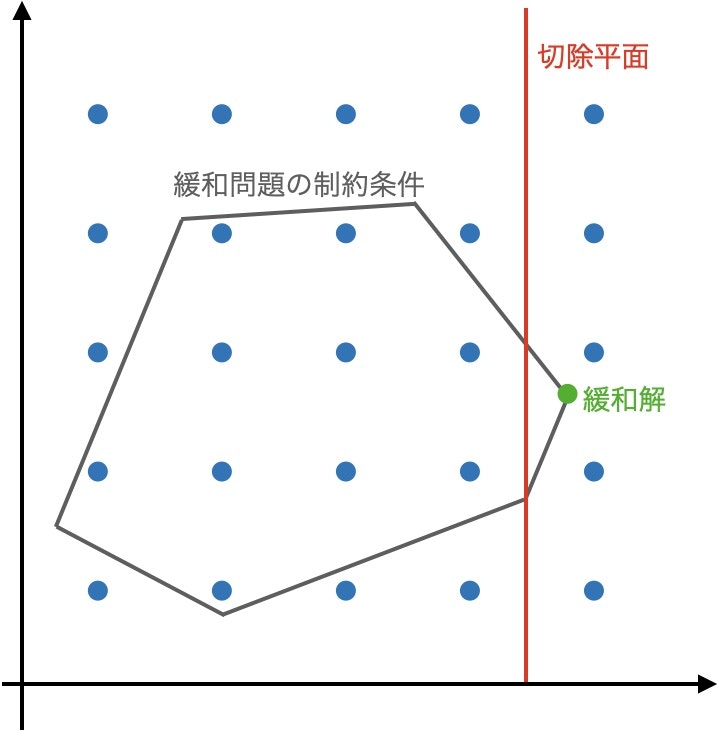
9.1.2 切除平面法 (Cutting-Plane Method)
線形緩和問題の最適解から始めて、整数解を残しつつ緩和解を除去する制約を追加する手続きを繰り返し適用する。妥当不等式 (整数解を残す制約) の中で緩和解を除くものを切除平面と言い、切除平面を追加することで解空間を狭めていく。
- 線形緩和問題を解く
- 緩和解が整数解なら終了
- 妥当不等式を追加して1.に戻る
9.2 近似解法
9.2.1 貪欲法
問題の意思決定対象に対し、局所的な情報だけで順に意思決定していく。例えばナップザック問題で、$p_i/w_i$ が大きいものから順に商品を選んでいくなど。
一般には近似解しか得られないが、クラスカル法・プリム法・ジョンソン法などでは厳密解を得られる。
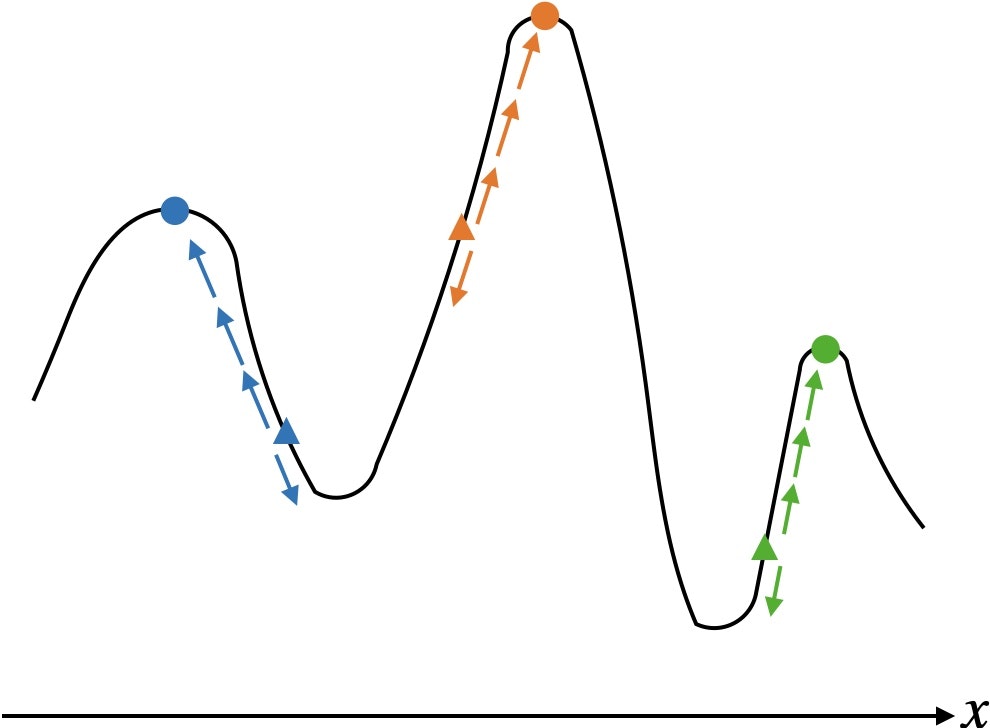
9.2.2 局所探索法
名前の通り今得られている解の近傍を探索していく。
- 初期解 $\boldsymbol{x}$ をいずれかの方法により構築する
- 解 $\boldsymbol{x}$ の近傍内によりよい解があれば解 $\boldsymbol{x}$ を更新し、ステップ2に戻る。よりよい解がなければ終了する。
ナップザック問題を例にとると近傍には以下のようなものがある。
- 挿入近傍:リストに入っていない品物を1つ選び、リストに入れる
- 交換近傍:リストに入っているものから1つ、入っていないものから1つ選び交換する
- $k$-opt近傍:$k$ 個の要素を変化させる。リストに入っているものから $k-l$ 個、入っていないものから $l$ 個選び交換する、など
一般に大域的最適解には到達できないが、局所的最適解は比較的容易に求められる。
9.2.3 メタヒューリスティクス
問題に依存しない形式で近似的に解を探索・改善する手法。以下のような工夫によりよい解を得られる。これらをバランスよく実現することが重要。
- 集中化:よい解周辺を集中的に探索する
- 多様化:局所的最適解に陥らないように、幅広く探索する
9.2.3.1 多スタート局所探索法 (Multi-start Local Search)
初期解を変えて局所探索法を繰り返す方法。初期解の作成には乱数を用いる。
途中までの局所最適解を初期解に反映させる方法もある。適応的多スタート局所探索法という。
9.2.3.2 遺伝的アルゴリズム (Generic Algorithm)
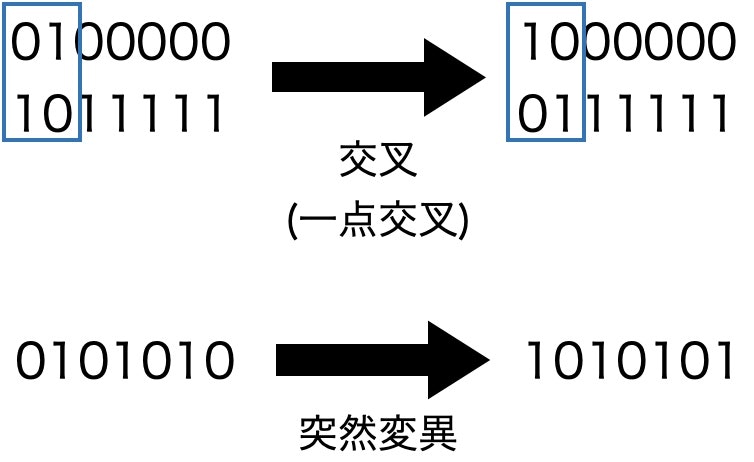
解を遺伝子として表現し、複数の遺伝子を用いて交叉や突然変異などの操作と淘汰による世代交代によって、解を探索する。
交叉や突然変異は以下のイメージ。
9.2.3.3. 粒子群最適化 (Particle Swarm Optimization)
多数の粒子によって集団を形成し、集団に含まれる粒子同士が情報交換することにより探索を進める。
- 初期化:すべての粒子 $k$ に対して、初期位置 $x_k(0)$ と初期速度 $v_k(0)$ を与える
- 位置更新:速度を用いて粒子の位置を更新する。$x_k(t+1)=x_k(t)+v_k(t)$
- 速度更新:よい解の方向に向かうように速度を更新する。$x_k^p(t)$ は $k$ 番目の粒子の中での過去最良解、$x^g(t)$ はタイムステップ $t$ における最良解、$w, c, r$ は定数。
v_k(t+1)=wv_k(t)+c_1r_1\left(x^{p}_k(t)-x_k(t+1)\right)+c_2r_2\left(x^{g}(t)-x_k(t+1)\right)
9.2.3.4. 焼きなまし法 (Simulated Annealing)
高温状態からはじめ、探索を繰り返す中で低音状態にしていく。高温では改悪を含む探索を許容、低温では通常の局所探索をすることで、局所最適解に陥らないようにする。
- 初期温度 $T$ を設定する
- 初期解を設定する
- 冷却率 $\alpha$ で温度を下げる。$T←\alpha T$。
- 次の解をランダムにサンプリングする。
4-1. サンプリングした解が現在の解よりよい場合、更新する。
4-2. サンプリングした解が現在の解より悪い場合、改悪幅 $\Delta E$ に対して確率 $\displaystyle Prob\left(U(0,1)>\exp\left(-\frac{\Delta E}{T}\right)\right)$ で更新する。 - 閾値を満たす解を得られるまで3.と4.を繰り返す。
9.2.3.5. 人工蜂コロニーアルゴリズム (Artificial Bee Colony Algorithm)
ミツバチの採餌行動を模す。収穫バチ・追従バチ・偵察バチを定義。
- 収穫バチ:1つの食糧源に蜜を取りに行き、その近傍も探索する
- 追従バチ:収穫バチの情報に基づいて目標の食糧源を決め、蜜を取りに行く
- 偵察バチ:食糧源の蜜が尽きたら新しい食糧源を決める。
以下のようなアルゴリズム。
- 初期食糧源を生成する
- 収穫バチフェーズ。自分の食糧源近傍を探索し、よりよい食糧源があれば更新する。また、蜜の取得回数をインクリメントする
- 追従バチフェーズ。評価値の高い食糧源を高確率で選択し、蜜の取得回数をインクリメントする
- 偵察バチフェーズ。指定回数以上蜜を取得した食糧源を、他の食糧源に置き換える。探索の打ち切りを示す
9.2.3.6. タブー探索法 (Tabu Search)
タブーリストと呼ばれる過去の更新履歴を用いて、同じ解への探索をしないようにする。局所解に落ちないための工夫。
- 基準個体を生成する
- 近傍個体を生成する (タブーリストに含まれる個体は生成しない)
- 基準個体から最良個体への遷移をタブーリストに追加 (最良個体そのものをタブーリストに追加する場合もある)
- 最良個体を基準個体にする
- 最良個体が終了条件を満たせば終了、それ以外の場合2.に戻る。
9.2.4. 列生成法 (Column Generation Algorithm)
パターンを全列挙すると膨大になり線形緩和問題を解くのも難しい場合に、パターンを一部だけ列挙して近似解を得る方法。