Pytorchを使ってDLを組んでるときに、畳込みとプーリングが曖昧な理解だった気がするので、
忘れたら見に来れるようにメモる
局所受容野
視覚野のニューロンが反応する範囲のことを受容野と呼ぶらしく、
ニューロンが入力のごく一部にだけ応答する性質を局所受容野というらしい
詳しい定義はこちら
局所受容野のニューロンには2種類あり「単純型細胞」と「複雑型細胞」
この2つに対応してるのが畳み込みとプーリング
単純型細胞はイメージ通りある特定の形状に反応する細胞で、その形状がずれると反応しない
ただ、いろんな形状に対応した単純型細胞が連携すれば複雑な形状の物体を認識することができる。
一方の複雑型細胞は形状の空間的なズレを抜き取る。
単純型は形状が変わると別の細胞の形状になってしまう。
複雑型細胞は空間的な位置ずれを抜き取り、同一形状と見なせるように働く
そうすることで空間的な位置ずれがあっても同じ形状で認識することが可能
畳み込み層
まず大雑把にまとめると畳み込み層とプーリング層では入力のニューロンの一部の領域を絞り、限定的(局所的)に次の層へ対応付していきます。
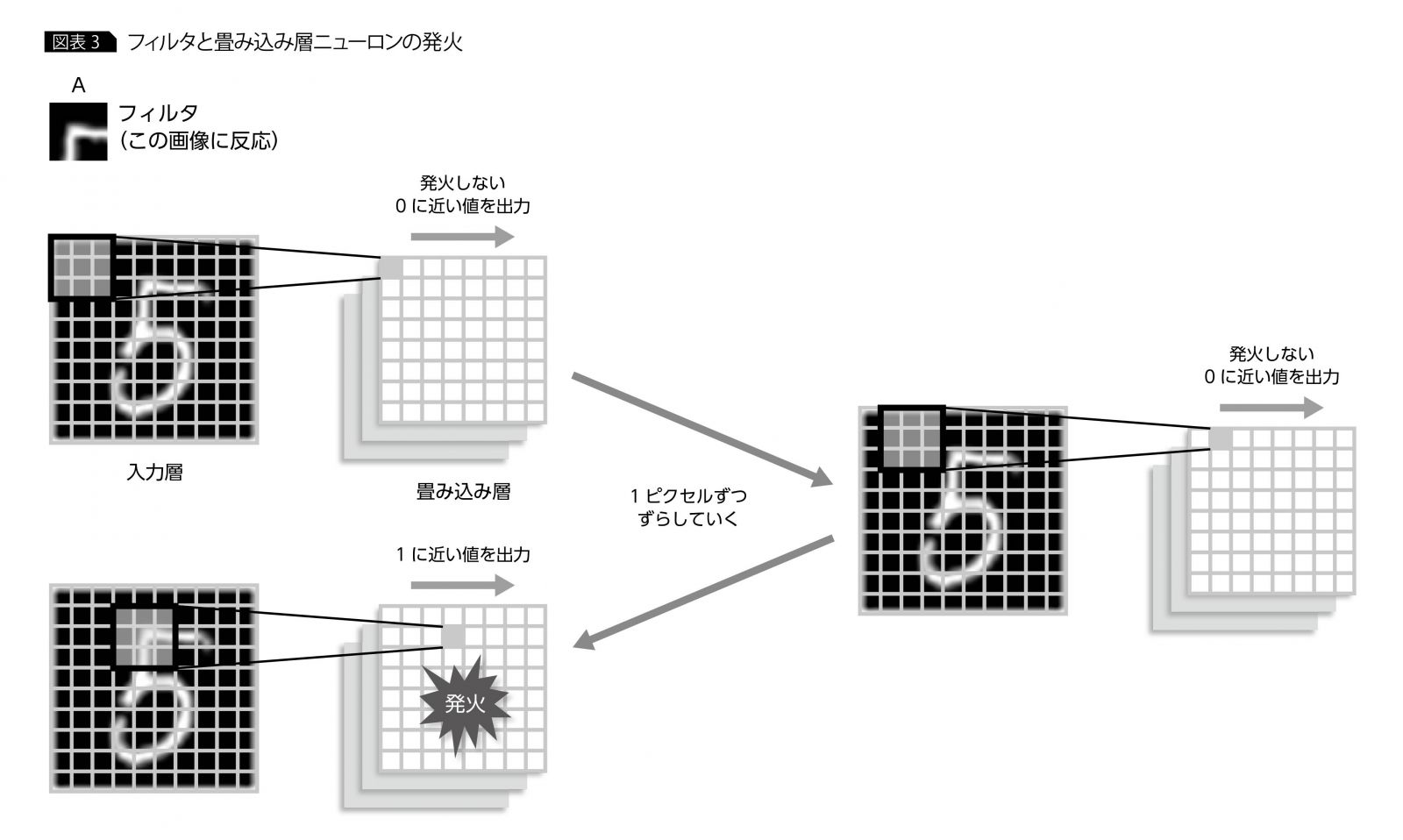
畳み込み層は単純型細胞をモデルにし、この特定の形状に対応するように構成されており、フィルターと呼ばれる
例えば、数値を認識する際の手がかりは数値の直線や曲線であり、それをフィルターとして設定する
ということは、フィルターの数が多いとそれだけ、様々な形状を持つことになる
畳み込みネットワークの構造は、最初の入力層で画像の1ピクセルが1ニューロンに対応し、
次に単純型細胞に相当する畳み込み層、そして複雑型細胞に相当するプーリング層と続く。
そのあとは、全結合層と出力層につながる。
- 局所受容野
- 単純型細胞 <-> 畳み込み
- 複雑型細胞 <-> プーリング
フィルターと一部の入力画像を対応させて、そのフィルターが局所受容野に見つかれば畳み込み層のニューロンが発火する
入力層と畳み込み層の間の結合を数式で表すと、
\sigma(b+\sum_{l=0}^{2}\sum_{m=0}^{2}w_{l,m}x_{{j+l}, {k+m}})
xが入力画像の各ピクセルの値、wが重み、bがバイアス、σが活性化関数
この数式のチューニング対象になるのは、wとbで、
NNと同様にCNNの出力値と正解の値との差が小さくなるようチューニングされる。
このwはフィルタで、判別に必要な形状になっている。
フィルタを複数構成することで識別性能があがりやすい
なぜなら、特定の形状に対応したフィルタを複数持てるので、
より正しく識別できそうなのは感覚的にわかる。
各フィルタに対応する畳み込み層内のニューロンセットをチャネルという
畳み込みの計算方法についてわかりやすかった例
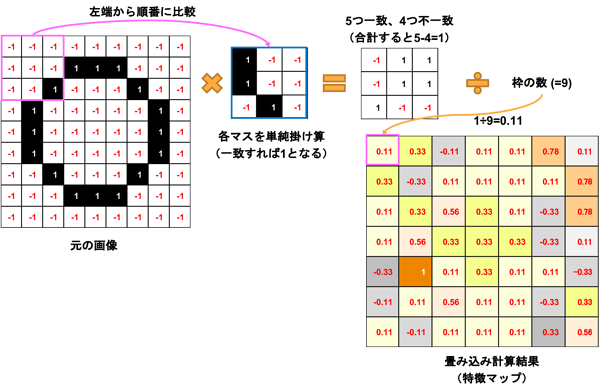
引用元
プーリング層
プーリング層は複雑細胞をモデル化したもの。
入力画像のフィルタ形状の位置ずれを抜き取る機能
目的は特徴をより強調すること
プーリング層の各ニューロンの出力が、畳み込み層のニューロンの出力値のなかで最大値を設定する
仕組みはプーリング層のニューロンの発火が、対応する畳み込み層のニューロンのどこかが発火したことを意味する。
入力データをより扱いやすい形に変形するために、情報圧縮を行い、ダウンサンプリングする。
圧縮する効果は
- 微小な変化位置に対して敏感になる
- ある程度の過学習を抑制できる
※随時更新
参考
ここでは自分が調べたこと覚えておきたいことを限定的に記述してます。
なので、話の流れが掴みにくいと思うので、個人的に
おすすめのサイトを貼っておきます。
CNNの理解のために先行研究も記述してくれてる
※随時更新