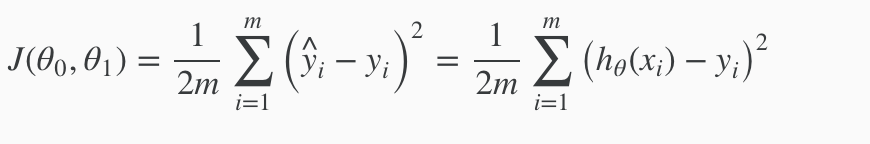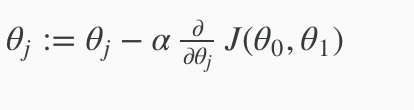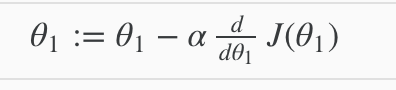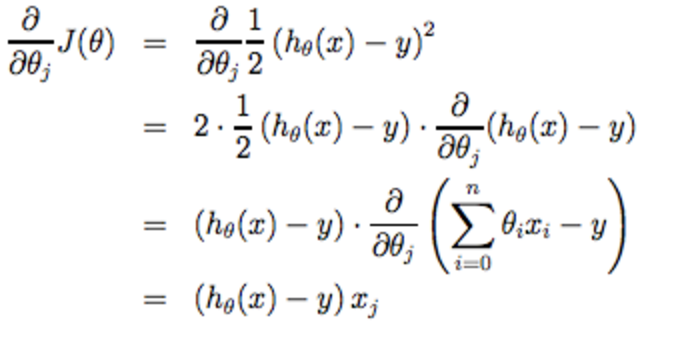Machine Learning by Stanford University WEEK1 のまとめ
#Introduction

What is Machine Learning? 機械学習とは何か？

代表的なものに以下2つの定義がある

• アーサー・サミュエルが提唱: コンピュータに明示的にプログラムすることなく学習する能力を与える研究分野
• トム・ ミッチェルが提唱: 課題=T, 性能基準=P, 経験=Eとし、課題 T について、 性能基準 P に基づき、T についての性能が P で測定して、経験 E と共に改善している場合に、 経験 E から学習したと言うことが出来る。
  • 例：課題T=天気予報,　経験E=実際の天気,　性能基準P=実際の天気と天気予報とが合致しているか

教師あり学習

• 教師あり学習では、入力値と出力値のデータセットのサンプルについて、「正しい答え」が与えられており、入出力の間の関係を学習アルゴリズムで定義する。

• 教師あり学習は以下ような問題に分類できる。

  • 回帰問題：　連続値的な出力を予測 ex)家の価格を予測
  • 分類問題：　離散値的な出力を予測 ex)腫瘍の大きさから良性か悪性かを予測

教師なし学習

• 教師なし学習ではデータセットとして「正しい答え」は与えられず、データセットが与えられるのみで、与えられたデータセットから、それを分類するアルゴリズムを予測する。
• 教師なし学習には以下のような種類がある。
  • クラスタリング：　ex)100万個の遺伝子データを自動的に寿命、出身地等に関連した幾つかのグループに分類する。
  • ノンクラスタリング：　ex)カクテルパーティー問題：カクテルパーティーのような人が多くいる場所で特定の人の声を抽出する

モデル定義とコスト関数

線形回帰

• 表記方法について　トレーニングセット(x(i),y(i))のiはi番目のトレーニングセット　というインデックスを意味する
  • ex)(x(1),y(1))=(1,2),(x(2),y(2)=(2,3)等
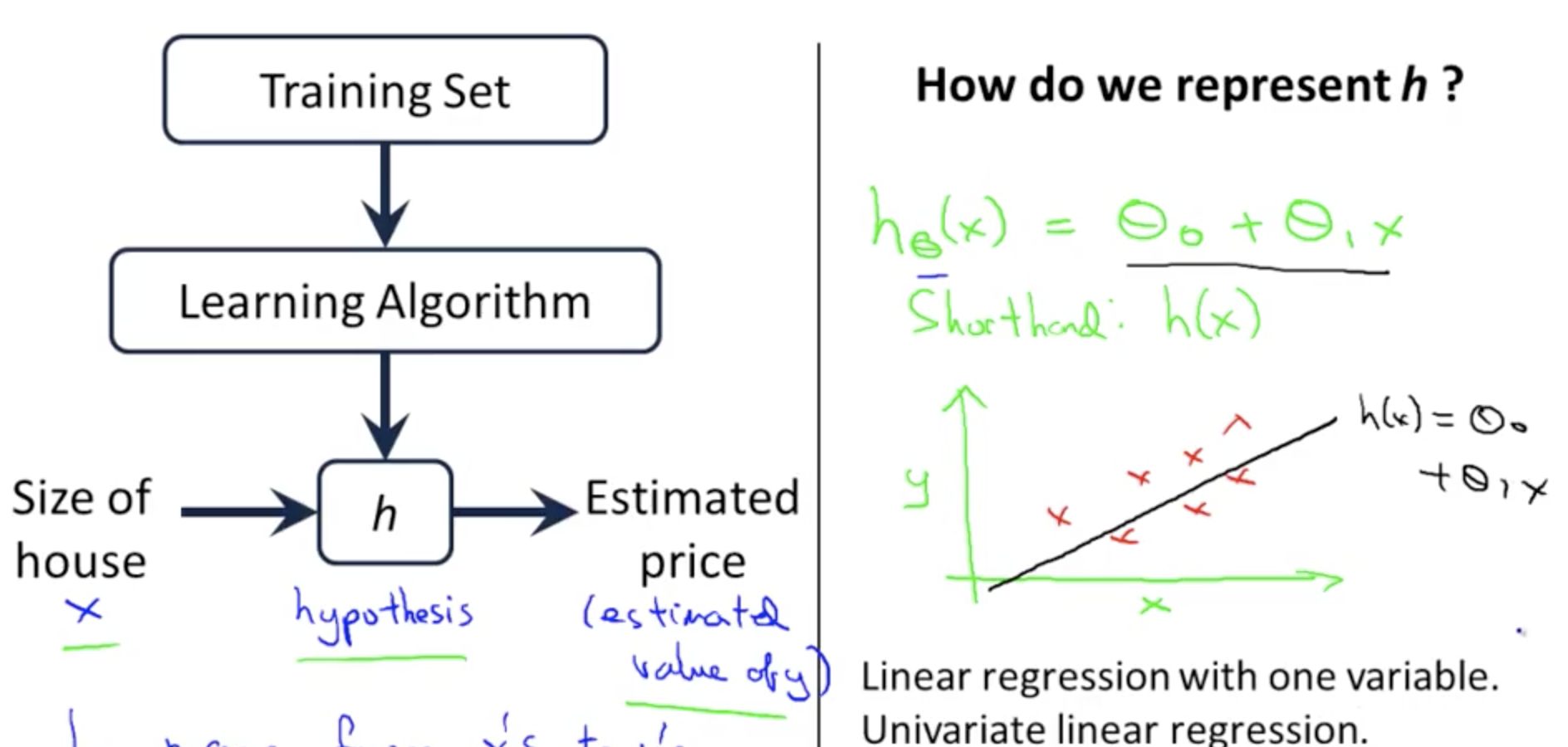
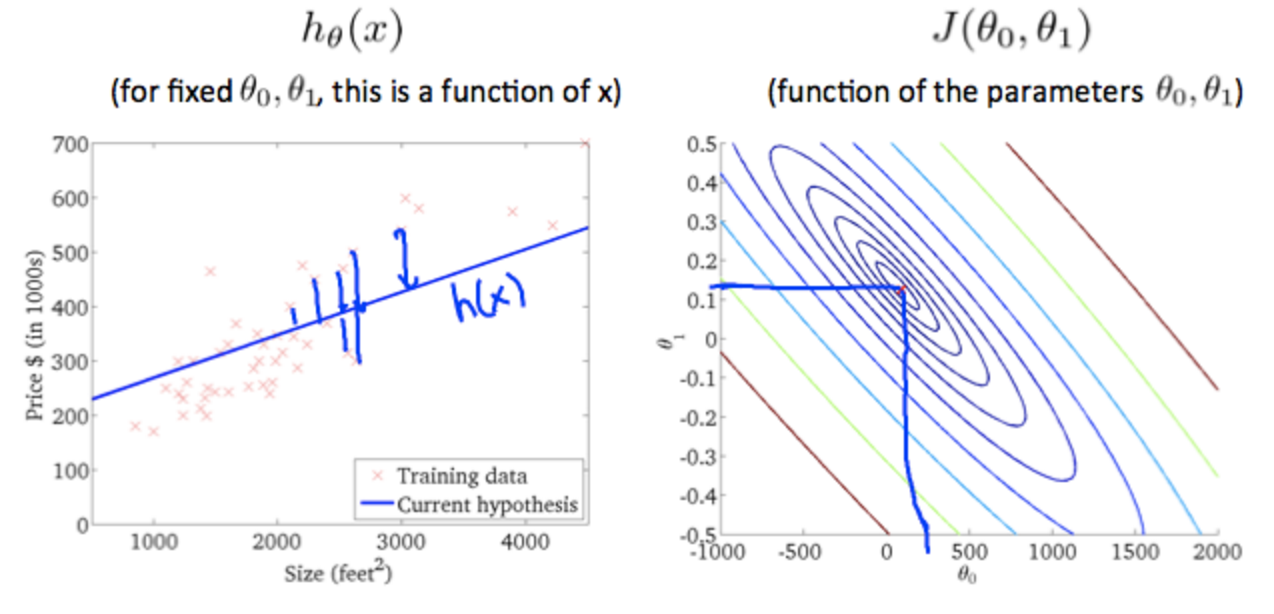
• 機械学習ではy = h(x)　（★h(x)はhypothesis function 仮説関数 と呼ぶ）の値が実際のyと一致するようにh(x)を求める。このh(x)には様々なモデルが考えられるが、良く使われるモデルの一つが線形回帰。線形回帰は以下のような式になる。

h(x) = thita_0 + thita_1*x 

参考スライドは以下

コスト関数

• 仮説関数h(x)が適当かどうかは、以下のコスト関数J(thita_0,thita_1)が0に最小となるかどうかで判定できる。
  

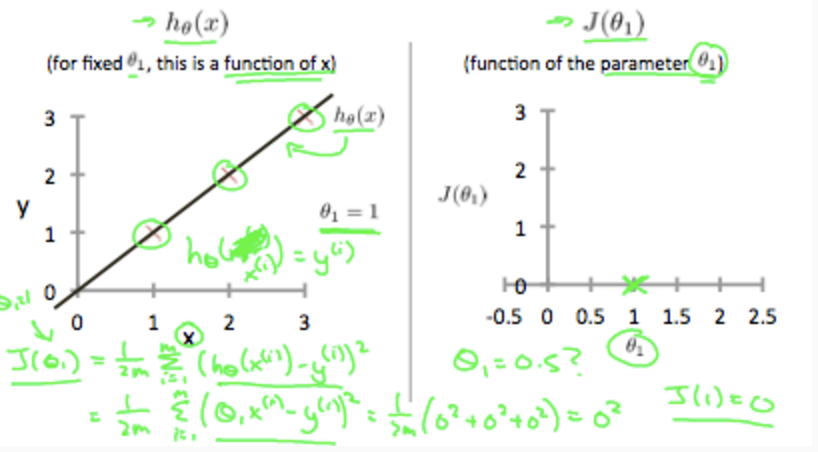
• (x,y) = ((1,1),(2,2),(3,3))のような学習データが与えられた時、コスト関数数J(thita_0,thita_1)が0となるthitaの値は thita_0 = 0 , thita_1 = 1となる。
  

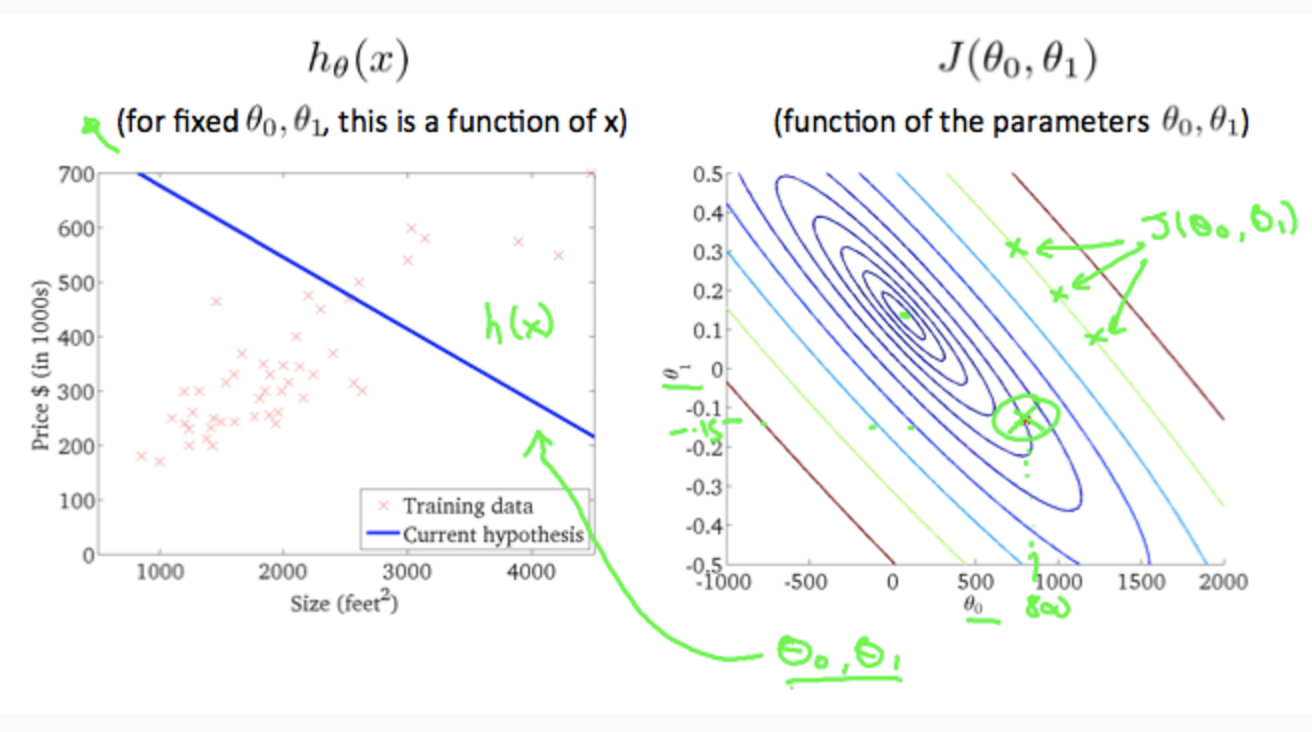
• thita_0 = 0 thita_1=0.5の場合、コスト関数Jは約0.58になる。
  同様にthita_0を0に固定しthita_1を変化させていくと、コスト関数J(thita1)は以下のようなグラフになる。
  

• thita_0を0に固定せずJ(thita0, thita1)を等高線で表すと以下のようなグラフになる
  

• コスト関数J→0 となるようなh(x)は thita_1=約0.12, thita_0=約250となる。
  

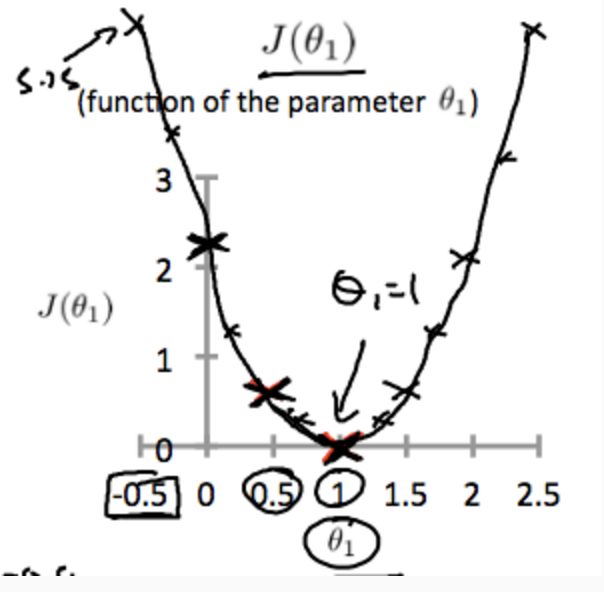
ParameterLearning

Gradient Decent 最急降下法

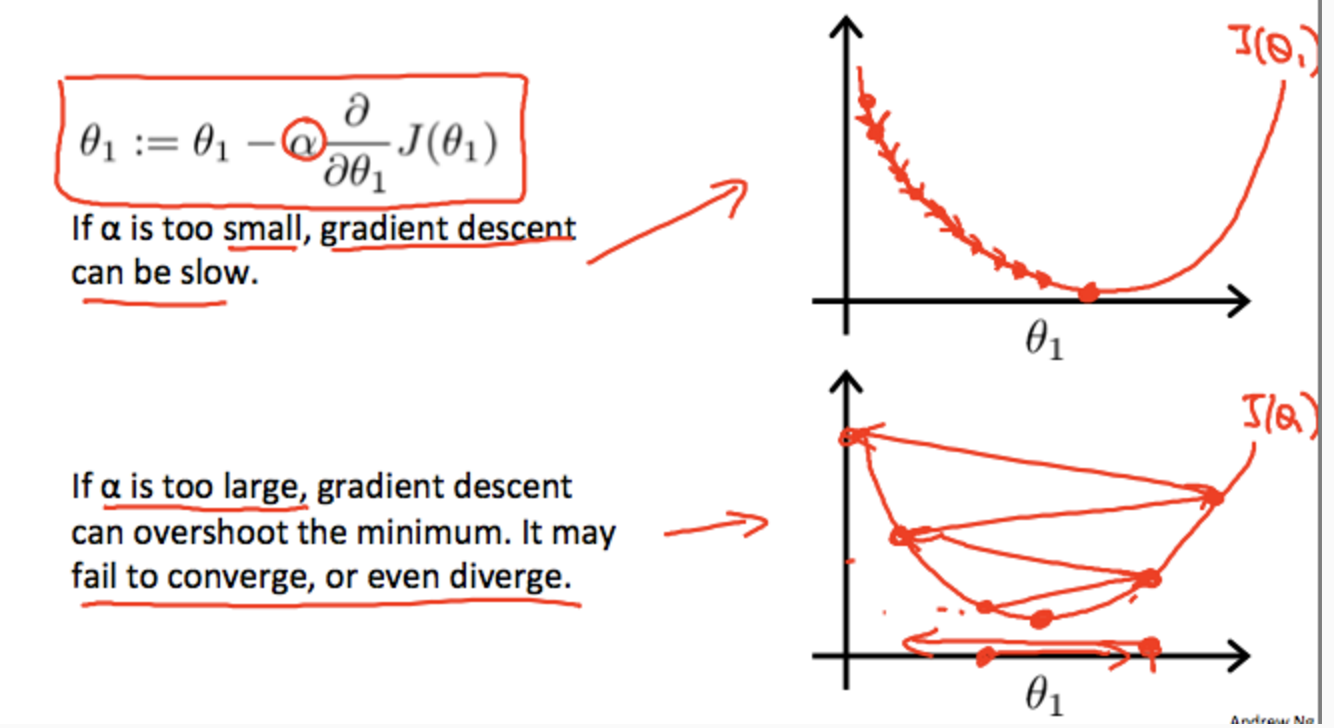
Jを最小化するthitaを求めるアルゴリズムの一つ、「最急降下法」について学ぶ。

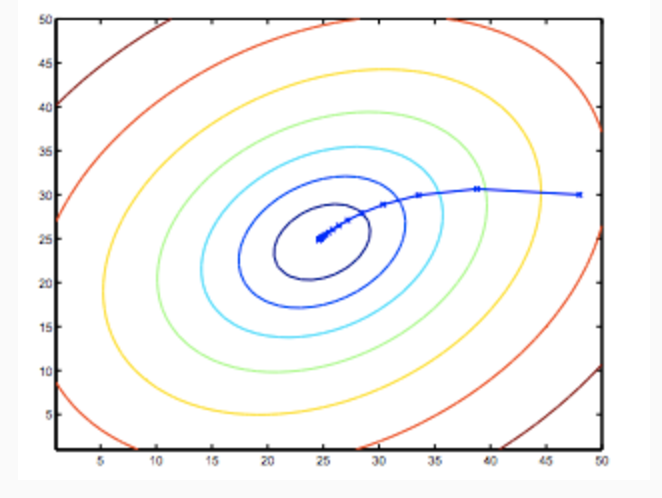
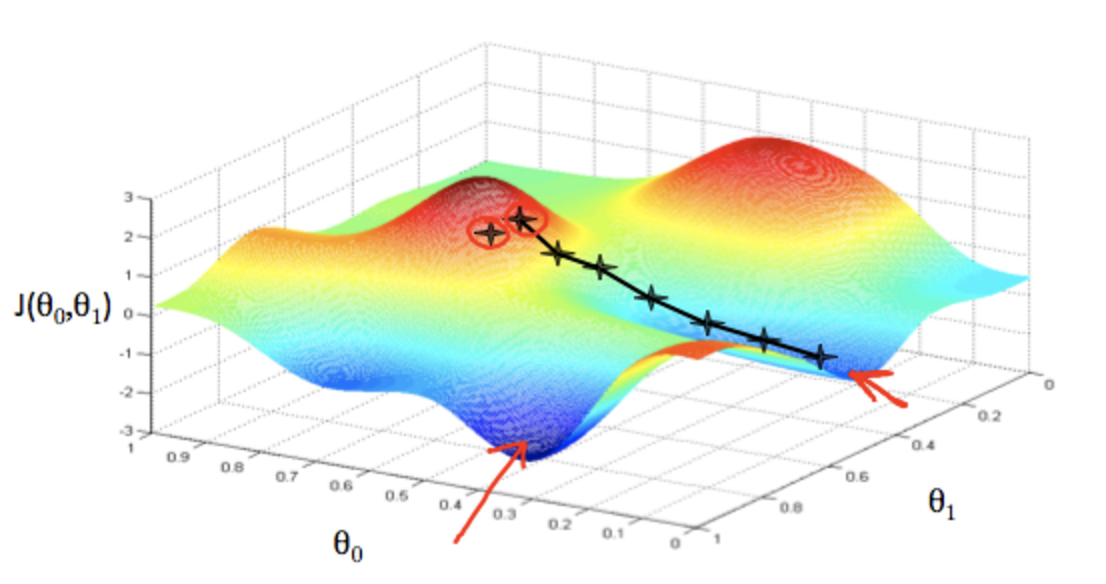
• 最急降下法は、例えば以下のようなJの最小点を探す際に、初期値に適当な値を取り、そこを出発点として、より小さな値を探索する方法。以下の例のように初期値により、異なる最小点（局所的最小点）にたどり着く事もある。
  

• 最急降下法は以下のような式で表せる。
  
  上記式でαは学習率と呼び、パタメータ更新次のステップの大きさを制御する。

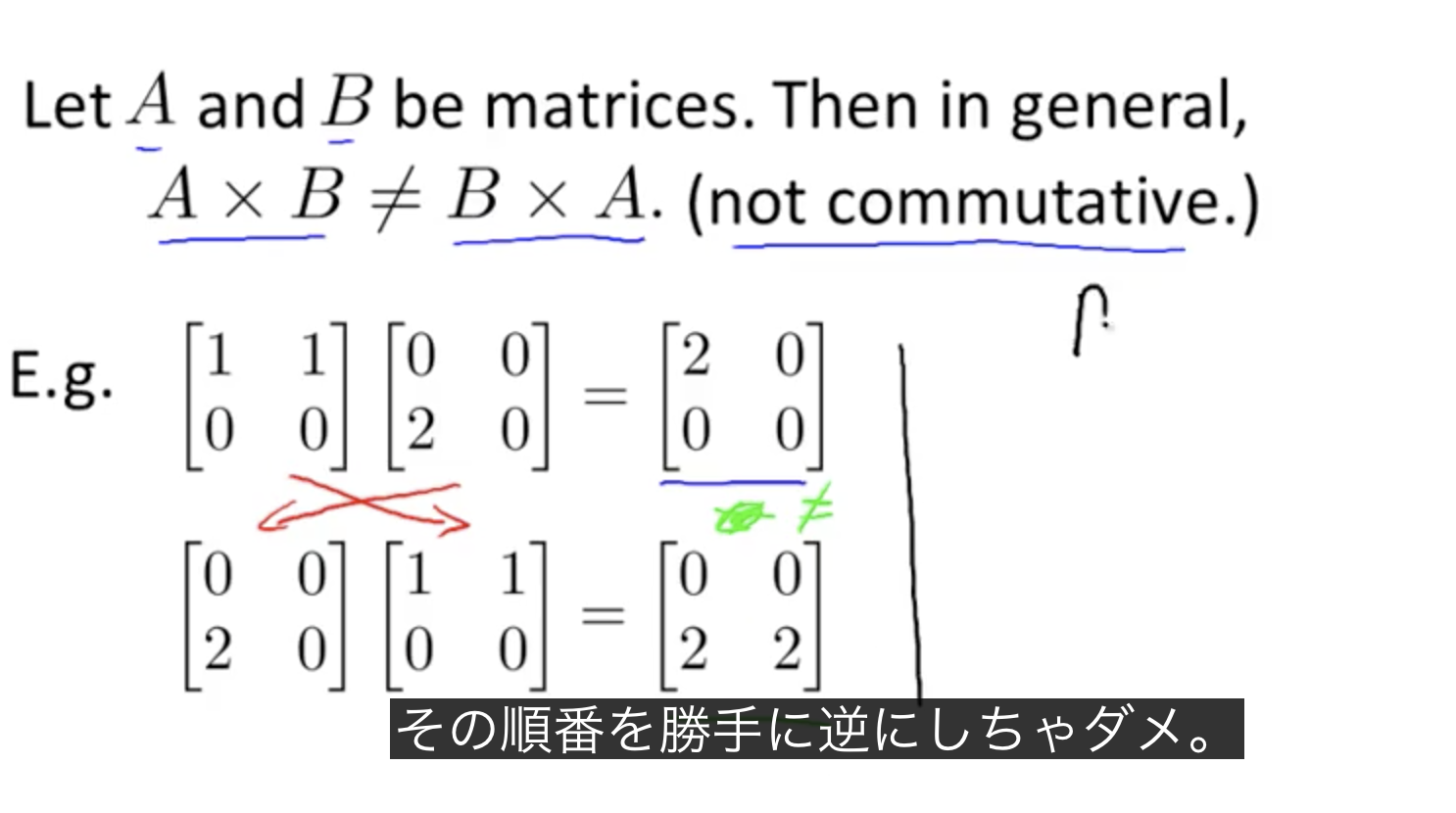
• 最急降下法の実装上の注意点は、「thita0とthita1は同時更新する」こと。以下の例では左が正。右は同時更新していない(thita0を先に更新してしまっている）ので誤り。
  

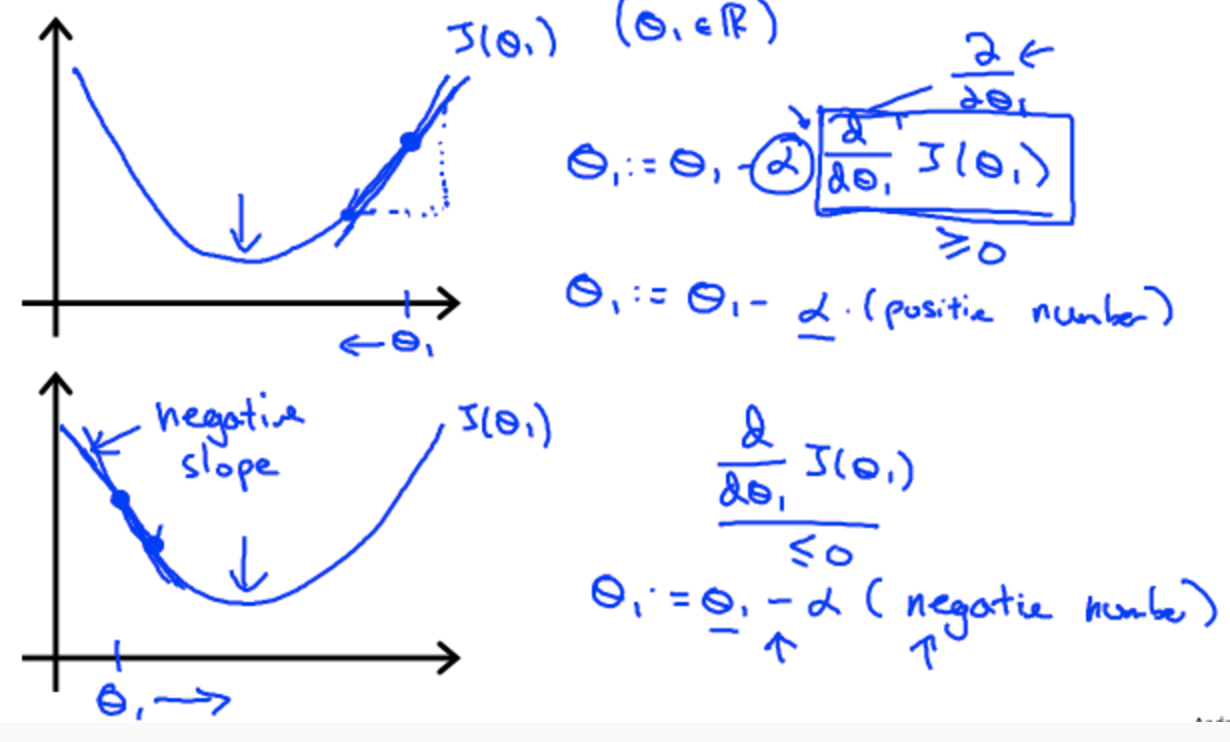
最急降下法の詳細

• 話を単純にする為に、最急降下法の式について、thita_0 = 0 固定とすると以下となる。
  

• 上記の式で、dj(θ)/dθ　はj(θ）の勾配を意味する
  

• 学習率αはθ更新時のステップの大きさ。小さすぎると学習に時間がかかり、大きすぎると発散する。
  

最急降下法とコスト関数

• コスト関数h(x)が線形(h(x) = thita_0 + thita_1*x)の場合、最急降下法に当てはめると、
  

より、

• θの値は以下の図のように収束する
  

線形代数の復習

行列とベクトル

行列とは

行列は2次元配列の別の呼び方にすぎない
ex)

行数×列数　の行列　と呼ぶ。上の例は4×2の行列　と呼べる。

行列の各要素

ベクトルとは

ベクトルは行列の一種にすぎない。 列が1の行列　つまり　n×1の行列。

行列の足し算

行列の足し算は、同一の次元の行列のみ可能。同一行番号、列番号の要素の和になる。
ex)

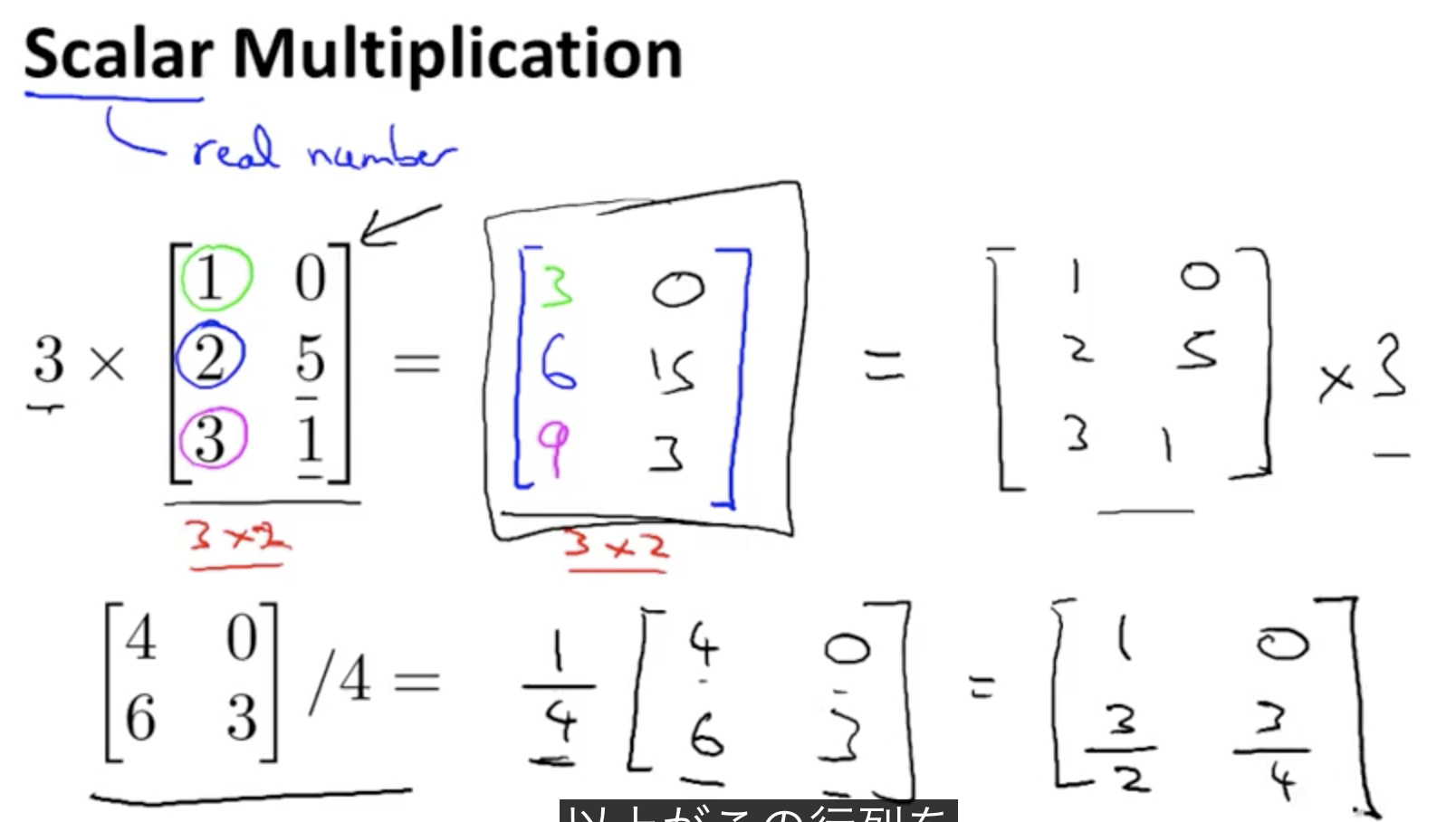
行列のスカラー値による乗算

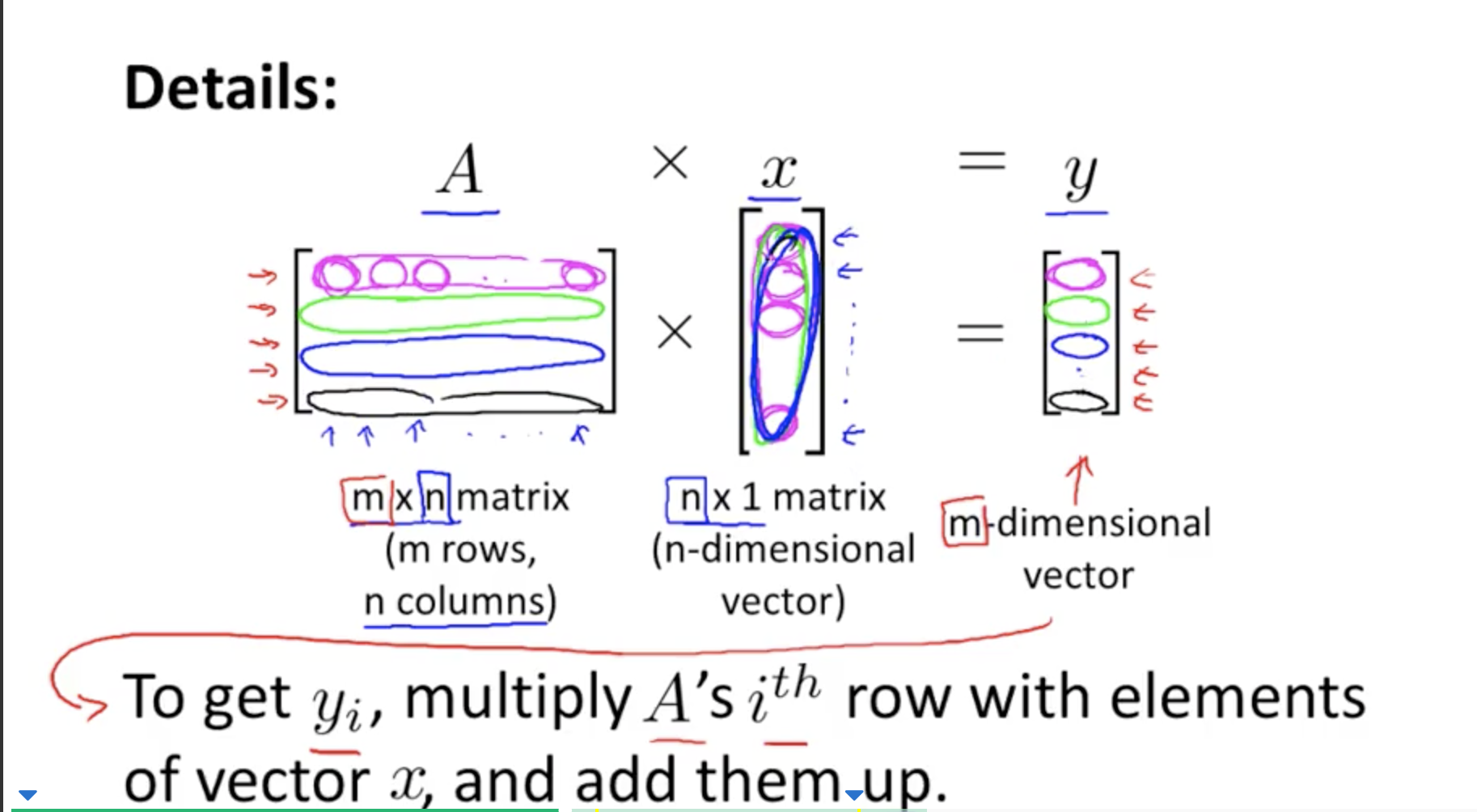
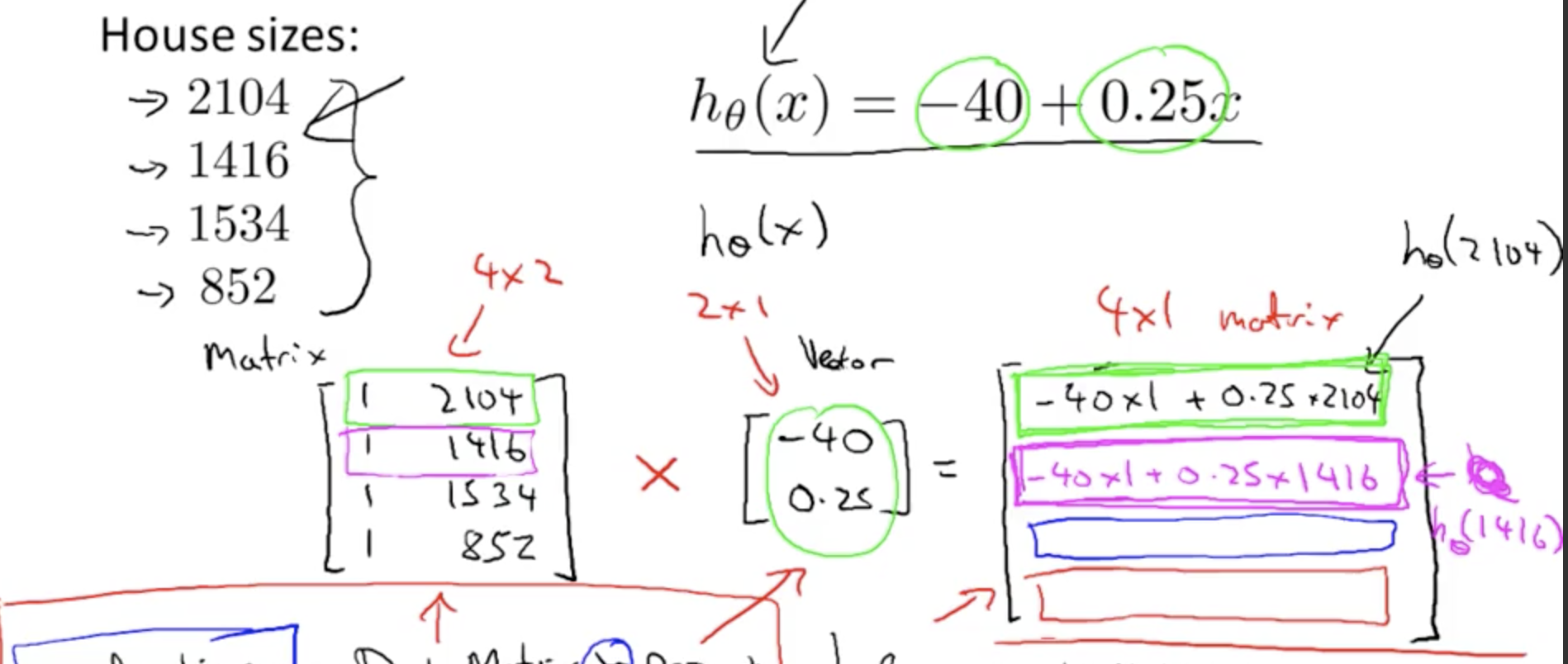
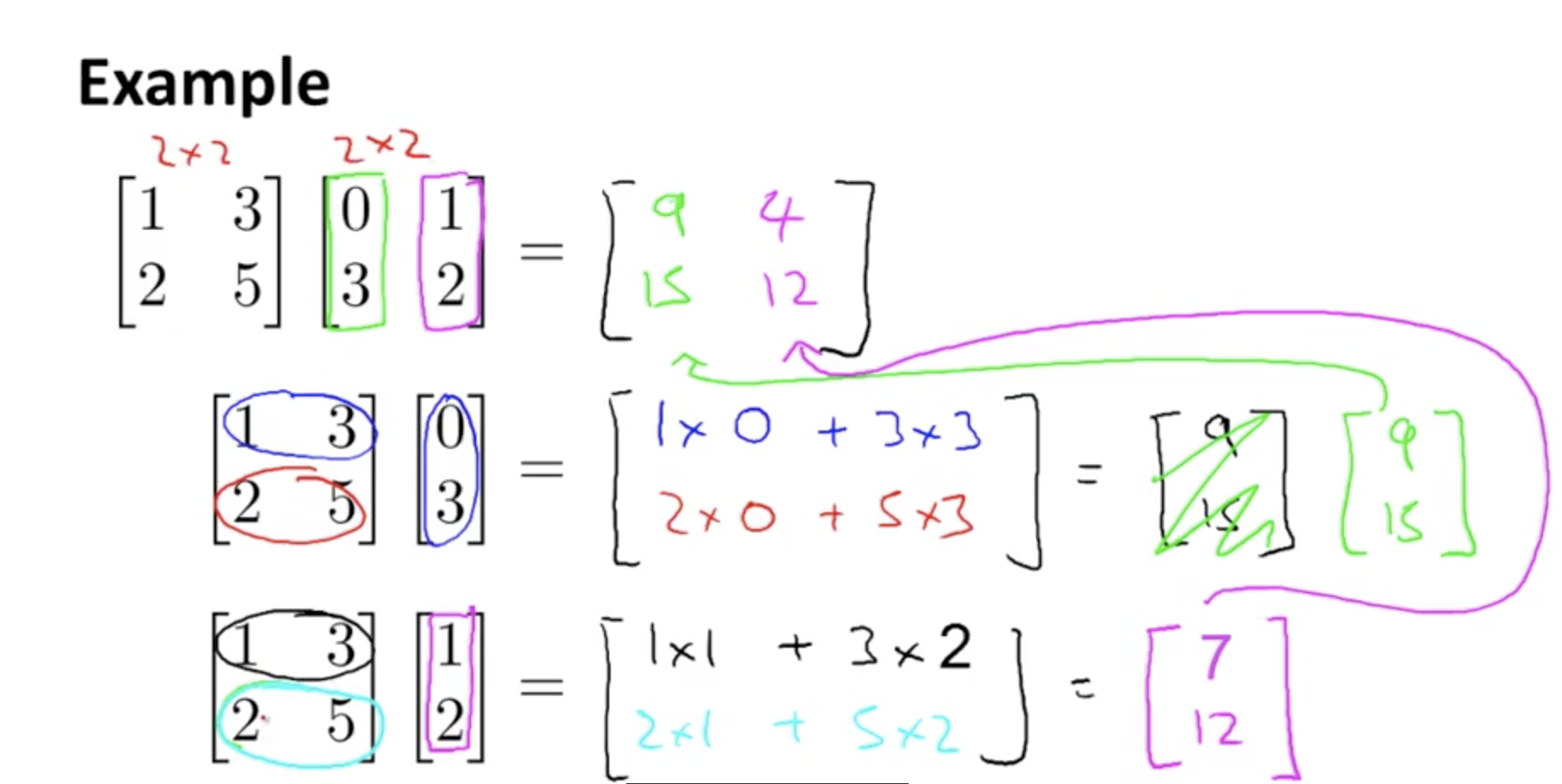
行列とベクトルの乗算

m×n 行列と n次元のベクトルの掛け算の結果はm次元のベクトルとなる。

• 線形関数h(x)の計算を行列とベクトルの乗算で表すと以下のようになる
  

行列同士の乗算

• 行列同士の乗算の例
  

• 行列の乗算は、順番を入れ替えると合致しない
  

• 対角線の要素が1、それ以外の要素が0の行列Iについては以下の法則が成立する。
  

逆行列と転置行列

逆行列

• 元の行列×逆行列=対角線上が1の行列になる
  
  逆行列は主要な言語のライブラリで求める事ができる。

• 逆行列を持たない行列は、特異行列または縮退行列と呼ばれる。
  ex)全ての要素が0の行列

転置行列

• 転置行列の例は以下　n×m行列の転置行列はm×n行列になる