今日は、競プロの計算量解析でよく出てくる、調和級数と割り算で出てくる項数の話をします。
計算量解析に失敗すると、実は解ける解法なのに解析に失敗したせいで解けないと思い込んでしまい、解かなかった、みたいなことが起こりかねないので、特に非直感的なこの2つについて押さえておきましょう。
調和級数
調和級数とは、$\sum_{n=1}^k \frac{1}{n}$ で表される級数です。
$k \rightarrow \infty$ とした時に正の無限大に発散することが知られていますが、発散は非常に遅いです。
さて、この調和級数は計算量解析にしばしば登場します。
1からNまでの間隔で長さNの数列を見ていく、みたいな処理の計算量見積もりには調和級数に関する知識が欠かせません。
先ほど述べたように調和級数の発散は非常に遅く、先頭 $N$ 項までの和は $\log N+1$ より小さいことが知られています。以下にこれの証明をします。
いきなりですが、
$\sum_{n=1}^k \frac{1}{n}\leq\int_{1}^{k}\frac{1}{t}dt+1$
です。
なぜでしょうか。グラフを描くとわかります。
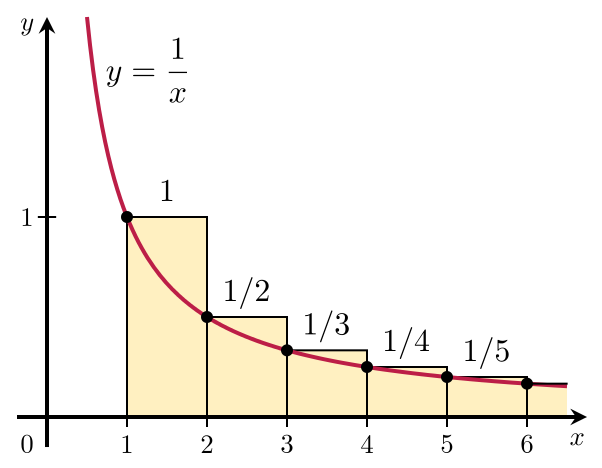
(Wikipediaより)
このグラフでは、式の左辺部分が長方形で、右辺部分が曲線 $y=\frac{1}{x}$ で表されています。
これ以外グラフが見つからなかったのでこれだけでは示せないのですが、このグラフを $1$ だけ $x$ 方向に平行移動すると、長方形の面積をグラフの面積が超えるようになります。
$\frac{1}{2}$ から先の部分はこのグラフの面積より小さくなるので積分で求められ、それに $1$ の部分だけを足せば上の不等式が出てきます。
では、具体的な値を求めましょう。積分をして、 $\log k+1$ ですね。
これで、$1$ から $\frac{1}{k}$ までの和が $O(\log k)$ に収まることがわかりました。
これを応用して計算量解析をする問題をいくつか挙げておきます。
ARC067-E Grouping
AGC038-C LCMs
ABC134-D Preparing Boxes(@Zen_Re_Kkyo 氏より提供)
AGC027-B Garbage Collector(@Zen_Re_Kkyo 氏より提供)
ARC068-E Snuke Line(@drken 氏より提供)
Mujin Programming Challenge-F チーム分け
割り算で出てくる項数
似たような話題で、$n$ を $1$ から $n$ までの整数でそれぞれ割って小数点以下を切り捨てた時、全部で何種類の整数が出てくるか?という問題があります。
これも実は $O(\sqrt n)$ 程度に押さえられるのですが、あまり厳密な証明は知られていません。
以下に証明します。
$m^2\leqq n< (m+1)^2$
を満たす整数 $m$ をとります。 $m$ は、$\sqrt n$ の小数点以下を切り捨てたものでもあります。
$m$ 未満の $i$ について、次が成り立つことを示します。
$[\frac{n}{i}]>[\frac{n}{i+1}]$
$\frac{n}{i}-\frac{n}{i+1}=\frac{n}{i(i+1)}>\frac{n}{(i+1)^2}\geq\frac{n}{m^2}\geq1$
より、
$\frac{n}{i}-\frac{n}{i+1}>1$
から、示されました。
よって、$1$ 以上 $m$ 未満の任意の i について、$[\frac{n}{i}]$ は、全て異なる値をとります。
次に、$1$ 以上 $m$ 以下の任意の値 $i$ が$[\frac{n}{m}]$ から $[\frac{n}{n}]$ までに登場し、かつそれ以外の値は現れないことを示します。
$n$ を $i$ で割った商を $k$, 余りを $j$ とします。
ここで、$i\leq k$ より、$k\geq m\geq i>j$ です。
よって、$k>j$ から、$n$ を $k$ で割った商は $i$, あまりは $j$ です。
これより、$[\frac{n}{k}]=i$ で、また、$k\geq m$ なので、任意の $i$ が$[\frac{n}{m}]$ から $[\frac{n}{n}]$ までに登場し、かつそれ以外の値は現れないことが示されました。
これらから、$[\frac{n}{1}]$ から $[\frac{n}{n}]$ までには高々 $2m-1$ 種類の値しか出てこないことが示されました。
このような計算量解析を利用する問題も挙げておきます。
ABC132-F Small Products
技術室奥プログラミングコンテスト#2-E 歩くNPCたち(@drken 氏より提供)
CPSCO2019 Session1-G Game with Division(@drken 氏より提供)
diverta 2019 Programming Contest-D DivRem Number(@QCFium 氏より提供)
AOJ 2370 Rabbit Walking(@drken 氏より提供)
AOJ 3045 Painting(@drken 氏より提供)
おわりに
今回は理論中心の話になりましたが、計算量の見積もりを正確にすることはとても大切です。
計算量を見誤って時間を無駄にしたり解ける問題が解けなかったりするようなことがないようにしましょう。
問題例は随時募集中です。