今回は、Convex Hull Trickを履修したので解説記事を書きます。
Convex Hull Trick とは
COLOCON -Colopl programming contest 2018- Final-C スペースエクスプローラー高橋君
を解こうとして、わからなくて、解説を見て、詰まりました。
知らないデータ構造は勉強しなきゃだめですか？だめですね
ということで、やってみたので記事にします。
Convex Hull Trickは、次のような操作ができるデータ構造(?)です。
・直線集合に直線を追加する( $ax+b$ の形で）
・ある $x$ に対し、集合の中で最小値（最大値）をとるような直線の値を求める
愚直に実装すると、追加される直線の本数を $N$ 本、最小値クエリの数を $Q$ 回として、当然 $O(NQ)$ かかるのですが、Convex Hull Trickを使うことで、追加を含めても計算量を $O((N+Q)\log^2 N)$ （特殊な場合は $O((N+Q)\log N)$ とか $O(N+Q)$ にできます。）
全体的な方針
このようなグラフを考えてみます。
固定された $x$ について、選ぶ直線の傾きを増加させていったときにとる値は下に凸になります。
よって、直線集合をキーとしてソートしておくことにより、二分探索で最小値を求められます。
# 不要な直線の削除
さて、これを実現するには「不要な直線の削除」という操作が不可欠になります。
次のグラフを見てください。
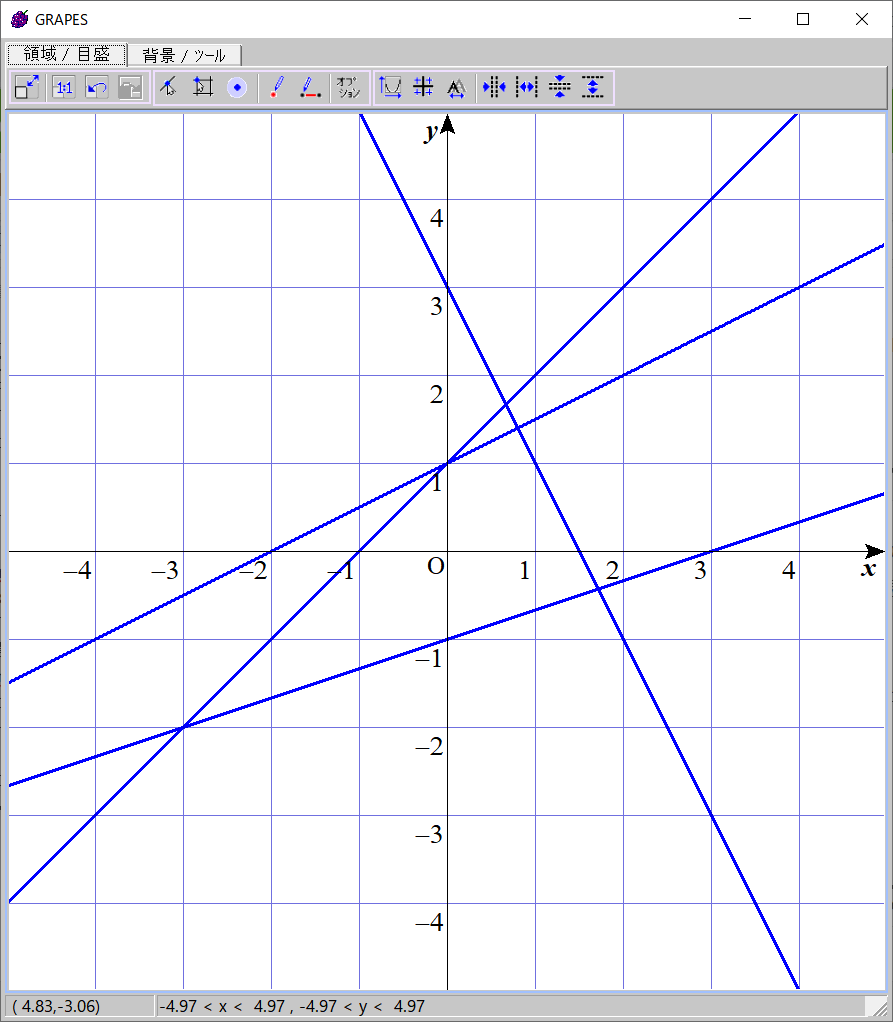先ほどのグラフにはなかった直線が追加されています。
また、この直線は、いかなる $x$ についても最小値をとらないので、不要です。
実は、このような不要な直線があると、先に挙げた凸性が成り立たず、二分探索ができなくなってしまいます。
そこで、このような不要な直線を取り除く操作が必要となります。
直線を追加する操作のたびにこの削除操作が必要になりますが、この操作がどんなときに必要か考えてみます。
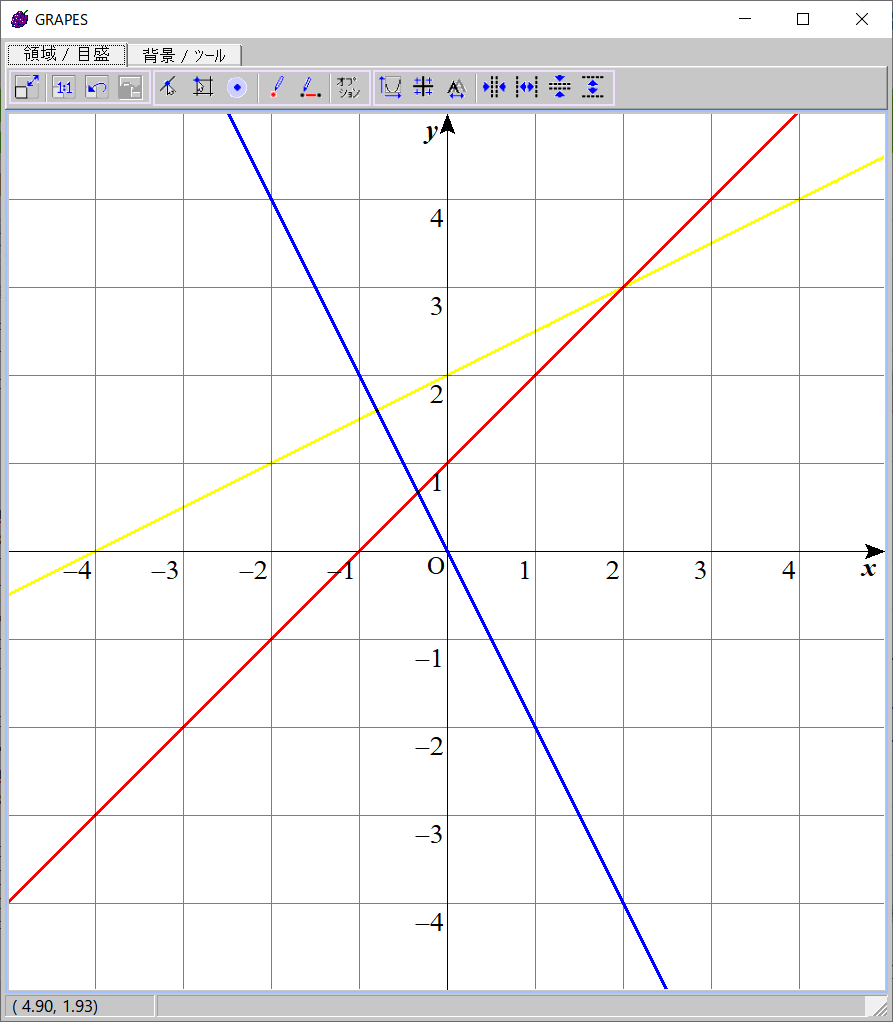黄色い直線を赤い直線と青い直線があるところに追加するときのことを考えます。
この黄色い直線は、
このとき、黄色と青の交点は赤と青の交点より左側（ $x$ 座標が小さい）にあります。
逆に、次のような場合を考えます。
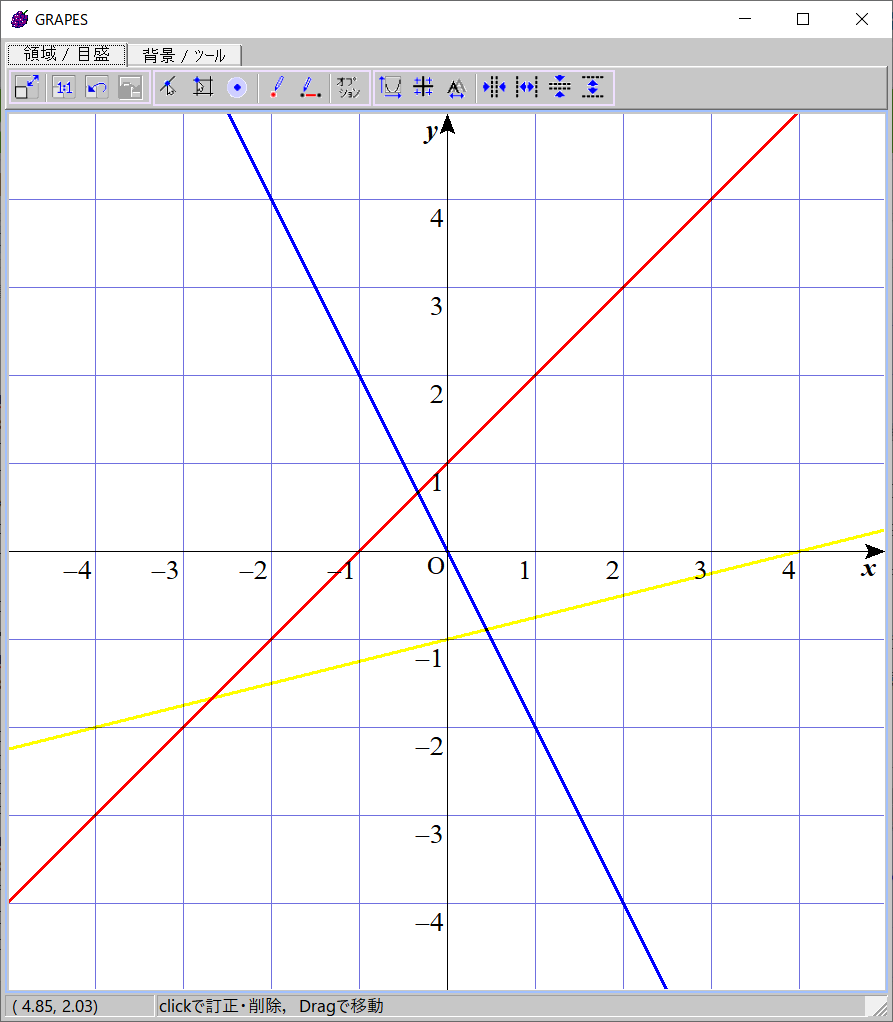この場合、上の場合とは逆に、黄色と青の交点は赤と青の交点より右側にあります。
結局、この交点の位置関係は、黄色の直線が赤と青の交点より下を通るか、つまり必要かどうかと対応するので、これを調べれば黄色の直線の必要性が判定できます。
黄色の直線が直線集合に入るとした時、傾きがその前後にある2直線の間に入り込むことになるので、傾きが前後にある2直線との判定を行えばいいです。
また、その前後の直線が不要になるか、なども同様に判定できます。
# 実装
上に挙げたように必要ない直線の削除を次のように行っていけばいいです。
・直線 $l$ を追加するとする。傾きが $l$ の前後に位置する直線をそれぞれ $l',l''$とする。
・直線 $l$ の必要性を $l',l''$ から判定する。必要なかったらここでおしまい。
・$l$ を追加したら、$l'$ の必要性も判定する。ここで $l'$がいらなかったらその前も、と以下同様に
・$l$ を追加したら、$l''$ の必要性も判定する。ここで $l''$がいらなかったらその後も、と以下同様に
削除される直線の数は最大で追加される直線の数だけなので、削除の計算量は特にボトルネックに影響を与えません。
直線の任意位置への追加と削除を効率的に行い、二分探索も行う必要があるので、std::mapなどの連想配列が適役です。
ただ、次に挙げる場合はmapを使う必要がないので計算量を削減できます。
・追加する直線の傾きが単調減少（単調増加）の場合
先頭や末尾にしか追加をしないので、std::vectorやstd::dequeで十分です、logがひとつ落ちます。
・クエリで与えられる $x$ が単調減少（単調増加）の場合
std::dequeで先頭や末尾を削除しながらどんどん進んでいくと二分探索がいらなくなるので、logがひとつ落ちます。
・上の二つを同時に満たす場合
両方実装すればいいのでlogがふたつ落ちます。
同じような感じで、追加する直線の傾きが今までのすべての直線より大きいか小さいかのどちらかの場合、とかもできますがなかなかに意味不明なクエリなので気にしなくていいでしょう。
自分はこんな感じの、クエリの種類によって計算量が異なるタイプのデータ構造はそれぞれ最適に実装したくなるんですが、「logがふたつついてもしらん！」みたいな人は、mapだけで実装してライブラリ化してもいいと思います。
実装を分ける場合は、クラスにしてコンストラクタ引数で種類を見分けるとらくです。引数を忘れて使うとき困りそうな場合は別のクラスに継承して自分で分かる名前にしておくともっとらくです。自分はセグ木とかはこうしています。
サンプルコード
現在実装が完成している、直線追加クエリの単調性にのみ対応したものを貼ります。
Convex Hull Trick サンプル
N=100000で1.5倍以上速くなったので、logを落とすのは大事そうです。
おわりに
Convex Hull TrickはAtCoderではたぶんあまり出てきません（今更）
結構高度なアルゴリズムですが、JOI本選などで出てきそうな雰囲気の問題はいくらでも思いつき、また、最近のAtCoder企業コンテスト本戦などでも高度アルゴリズムがよく出るので書けて損はないでしょう。