前回
前回の記事では、サイン波を使って MIDI 譜面を再生するところまで作りました。最後に書いたコードの続きから作っていきます。
概要
今回はシンセの波形生成部であるオシレータを実装して、サイン波以外も鳴らせるようにします。また、音を聞きながらパラメータを動かせるように、リアルタイム再生機能もあわせて実装します。
1.基本波形を追加する
サイン波の他に実装するのはノコギリ波、矩形波、ノイズの三つの基本波形です。
ノコギリ波
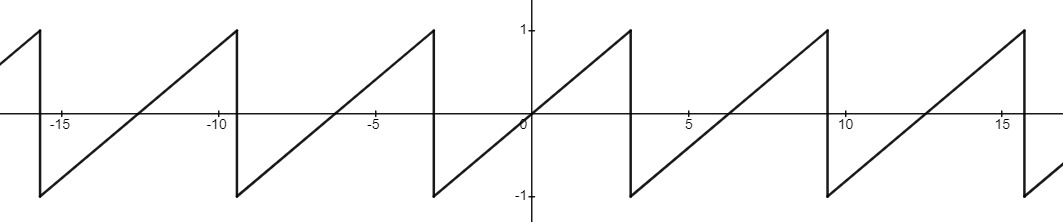
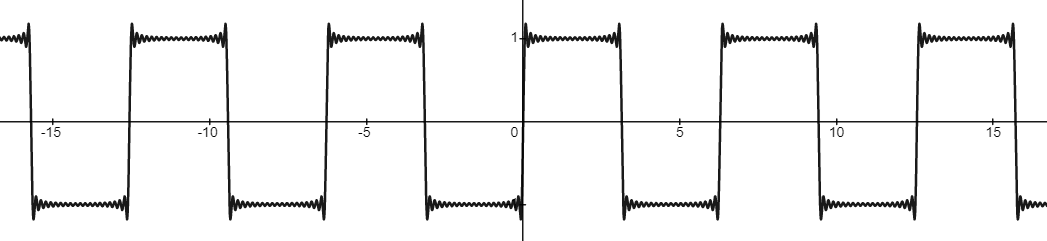
ノコギリ波はy=xを周期的に繰り返す波形です。周期はサイン波に合わせて $2\pi$ としています。この波形は剰余を使って以下のように書けます。
double SimpleWaveSaw(double x)
{
return 2.0 * fmod(x - Math::Pi, Math::TwoPi) / Math::TwoPi - 1.0;
}
試しに前回のコードのサイン関数呼び出しをそのままSimpleWaveSawに置き換えてみます。
-const auto w = static_cast<float>(sin(Math::TwoPiF * frequency * m_time) * envLevel);
+const auto w = static_cast<float>(SimpleWaveSaw(Math::TwoPiF * frequency * m_time) * envLevel);
再生波形の周波数を確認するために、リポジトリのSoundTools.hppにあるAudioVisualizerクラスを使って可視化を行うコードを追加します。
void Main()
{
auto midiDataOpt = LoadMidi(U"C5_B8.mid");
if (!midiDataOpt)
{
// ファイルが見つからない or 読み込みエラー
return;
}
const MidiData& midiData = midiDataOpt.value();
Synthesizer synth;
Audio audio(RenderWave(synth, midiData));
audio.play();
AudioVisualizer visualizer(Scene::Rect());
visualizer.setSplRange(-75, -50);
visualizer.setDrawScore(NoteNumber::C_5, NoteNumber::B_8);
while (System::Update())
{
if (KeySpace.down())
{
audio.stop();
synth.clear();
audio = Audio(RenderWave(synth, midiData));
audio.play();
}
visualizer.setInputWave(audio);
visualizer.updateFFT();
visualizer.drawScore(midiData, audio.posSec());
}
}
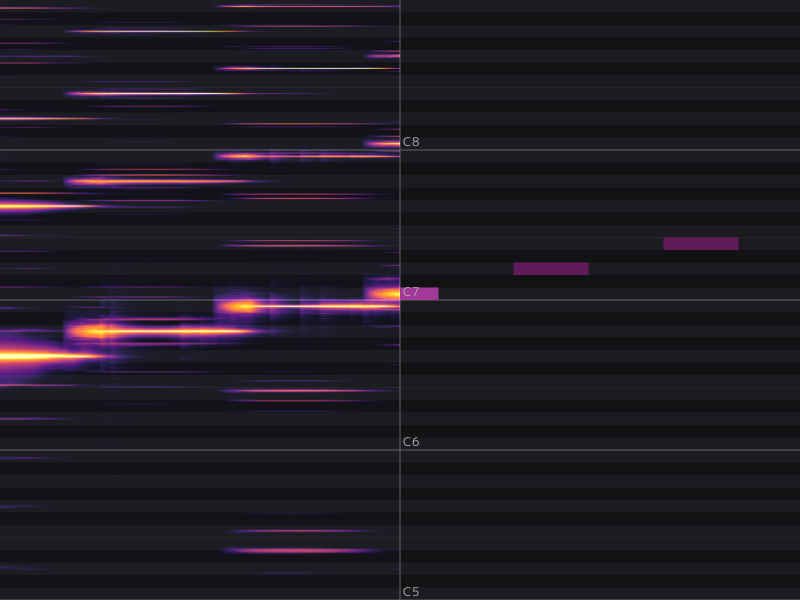
実行すると以下のような図が出てきます。画面の右は入力している MIDI 譜面、左は再生している音の周波数を音階上に表示したものです。
ノコギリ波は入力周波数の整数倍の倍音を含む波形なので、低い順から1オクターブ上、3倍音、2オクターブ上、5倍音、… といった周波数成分が現れるはずです。しかし、結果を見ると明らかに1オクターブ以内の周波数が入っていたり、入力よりも低い周波数が現れていたりと、ノコギリ波の周波数分布とは異なる音が出ているということがわかります。
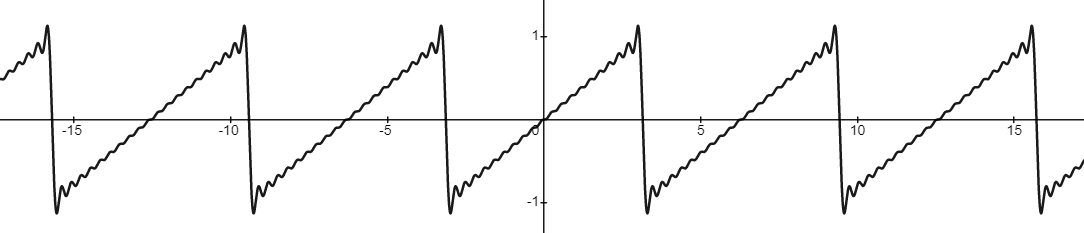
これは波形が不連続点を持っていることが原因で、ナイキスト周波数を超えた成分が折り返されて低周波数のエイリアシングとして現れています。したがって、実際に使うノコギリ波は冒頭で書いた離散変化を伴うものではなく、それを連続関数で近似した形のものです。
これを作るために、ノコギリ波をフーリエ級数展開した以下の式を使います。引数 $m$ は何項目まで展開するかを指定する値で、$m$ を大きくするほど元のノコギリ波に近づいていきます。
$$
w_{saw}(x, m) = -\frac{2}{\pi} \sum_{k=1}^m \frac{(-1)^k}{k} \sin(kx)
$$
この式のサイン関数がナイキスト周波数を超えないギリギリまで足し合わせてやれば、エイリアシングを取り除いたノコギリ波が得られます。
double WaveSaw(double x, int m)
{
double sum = 0;
for (int k = 1; k <= m; ++k)
{
const double a = (k % 2 == 0 ? 1.0 : -1.0) / k;
sum += a * sin(k * x);
}
return -2.0 * sum / 1_pi;
}
m の決め方
上式 $x$ の係数が $k$ であることから、このサイン波は入力の $k$ 倍の周波数を持っています。つまり、周波数 $f$ のノコギリ波がナイキスト周波数 $f_n$ を超えないためには、最大周波数の $m f \leq f_n $ を満たすように $m$ を設定する必要があります。
$$
m = f_n / f
$$
結果を確認するために、再び先ほどのコードをWaveSawで置き換えて再生してみます。
const uint32 SamplingFreq = Wave::DefaultSampleRate; // サンプリング周波数
const uint32 MaxFreq = SamplingFreq / 2; // ナイキスト周波数
-const auto w = static_cast<float>(SimpleWaveSaw(Math::TwoPiF * frequency * m_time) * envLevel);
+const int m = MaxFreq / frequency;
+const auto w = static_cast<float>(WaveSaw(Math::TwoPiF * frequency * m_time, m) * envLevel);
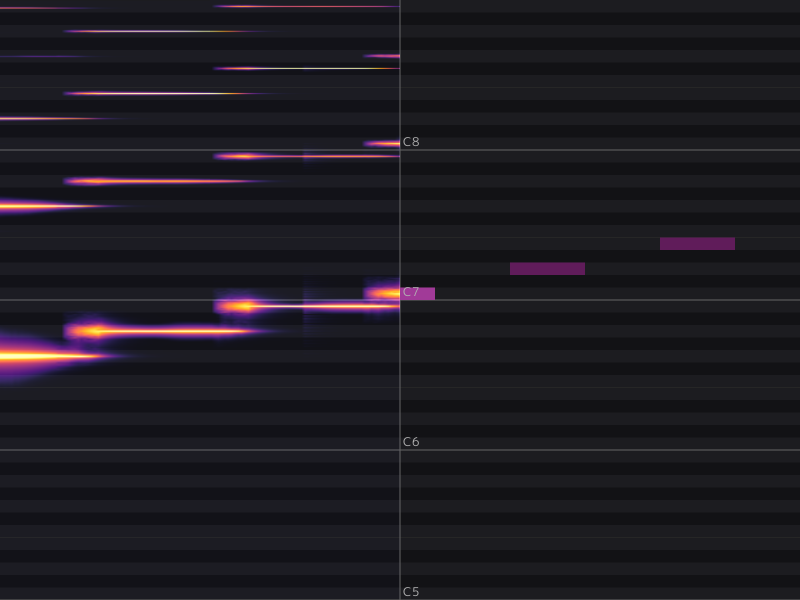
実行結果からエイリアシングが消えて正しい周波数分布を得られたことが確認できました。
矩形波
矩形波(パルス波)はオンオフの二値で表せる波です。こちらもノコギリ波と同様に、連続波形で表現するためにフーリエ級数展開した式を使います。
$$
w_{square}(x, m) = \frac{4}{\pi} \sum_{k=1}^m \frac{1}{2k - 1} \sin((2k - 1)x)
$$
double WaveSquare(double x, int m)
{
double sum = 0;
for (int k = 1; k <= m; ++k)
{
const double a = 2 * k - 1;
sum += sin(a * x) / a;
}
return 4.0 * sum / 1_pi;
}
m の決め方
今度は $x$ の係数が $2k - 1$ であることから、エイリアシングを防ぐには $(2m - 1)f \leq f_n$ を満たせば良いということがわかります。したがって、WaveSquare の場合は次式で計算した $m$ で波形生成を行います。
$$
m = (f_n + f)/2f
$$
ノイズ
一様分布する乱数列をそのまま音声波形にすることで、すべての周波数成分を等しく持つホワイトノイズを作ることができます。不要な周波数は後でフィルターを使って削ることができるので、波形に足りない周波数成分を補うのに有用です。
double WaveNoise()
{
return Random(-1.0, 1.0);
}
オシレータの実装
これまでに作った基本波形 Oscillator クラスにまとめておきます。
enum class WaveForm
{
Saw, Sin, Square, Noise,
};
class Oscillator
{
public:
double get(double t, double freq, WaveForm waveForm) const
{
switch (waveForm)
{
case WaveForm::Saw:
return WaveSaw(freq * t * 2_pi, static_cast<int>(MaxFreq / freq));
case WaveForm::Sin:
return sin(freq * t * 2_pi);
case WaveForm::Square:
return WaveSquare(freq * t * 2_pi, static_cast<int>((MaxFreq + freq) / (freq * 2.0)));
case WaveForm::Noise:
return WaveNoise();
default: return 0;
}
}
};
Synthesizer クラスには m_oscillator と、使用する波形の種類を指定する m_oscIndex を追加しました。
class Synthesizer
{
...
+ Oscillator m_oscillator;
+ int m_oscIndex = 0;
};
実験で何度か書き変えた波形生成部は、最終的に m_oscillator.get() の呼び出しにまとめました。
-const auto w = static_cast<float>(sin(Math::TwoPiF * frequency * m_time) * envLevel);
+const auto osc = m_oscillator.get(m_time, frequency,
+ static_cast<WaveForm>(m_oscIndex));
+const auto w = static_cast<float>(osc * envLevel);
ここまでのコード
差分のみ
コード全体
2.オシレータをウェーブテーブル化する
ノコギリ波のように、一つのサンプルを計算するたびに三角関数を何十回も呼び出すと時間がかかってしまいます。そこで、事前に波形を一周期分計算して配列に保存しておくようにします。この配列のことをウェーブテーブルと呼びます。
以下では Oscillator クラスを置き換える OscillatorWavetable クラスを実装します。
class OscillatorWavetable
{
public:
OscillatorWavetable(size_t resolution, double frequency, WaveForm waveType);
double get(double x) const;
private:
Array<float> m_wave;
};
ウェーブテーブルを生成する
まずコンストラクタでは resolution で指定された要素数の配列に波形を $[0, 2\pi]$ まで書き込んでおきます。
OscillatorWavetable::OscillatorWavetable(size_t resolution, double frequency,
WaveForm waveType) :
m_wave(resolution)
{
const int mSaw = static_cast<int>(MaxFreq / frequency);
const int mSquare = static_cast<int>((MaxFreq + frequency) / (frequency * 2.0));
for (size_t i = 0; i < resolution; ++i)
{
const double angle = 2_pi * i / resolution;
switch (waveType)
{
case WaveForm::Saw:
m_wave[i] = static_cast<float>(WaveSaw(angle, mSaw));
break;
case WaveForm::Sin:
m_wave[i] = static_cast<float>(Sin(angle));
break;
case WaveForm::Square:
m_wave[i] = static_cast<float>(WaveSquare(angle, mSquare));
break;
case WaveForm::Noise:
m_wave[i] = static_cast<float>(WaveNoise());
break;
default: break;
}
}
}
ウェーブテーブルの要素数には 1024 か 2048 の値がよく使われます。要素数を 2048 とすると、44100 / 2048 ≒ 21.5 [Hz] なので、これを下回った時に同じ要素が複数回サンプルされることになります。つまり、resolution=2048の場合、再生時の周波数が 21.5 [Hz] 以上であれば生成波形の周波数成分を失わずに再生することが可能です。
ウェーブテーブルを読み出す
次にウェーブテーブルを使用して波形を読み出す部分を実装します。$2\pi$ の周期で配列を一周すれば良いので、resolution / 2_pi を掛けてインデックスに変換し、resolution の剰余を取ってループさせます。
また、配列からサンプルを読む時は、サンプル同士の間を補間すると劣化がより目立ちにくくなります。線形補間で十分きれいになるのでその処理も追加します。
double OscillatorWavetable::get(double x) const
{
const size_t resolution = m_wave.size();
const double indexFloat = fmod(x * resolution / 2_pi, resolution);
const int indexInt = static_cast<int>(indexFloat);
// indexFloat の小数部分がそのまま補間係数になる
const double rate = indexFloat - indexInt;
return Math::Lerp(m_wave[indexInt], m_wave[(indexInt + 1) % resolution], rate);
}
シンセサイザーに組み込む
Synthesizer クラスのオシレーターを OscillatorWavetable で置き換えます。ウェーブテーブルはインスタンスによらず固定なので、グローバル定数として定義しておきます。
// とりあえず440Hzで生成
static const Array<OscillatorWavetable> OscWaveTables =
{
OscillatorWavetable(2048, 440, WaveForm::Saw),
OscillatorWavetable(2048, 440, WaveForm::Sin),
OscillatorWavetable(2048, 440, WaveForm::Square),
OscillatorWavetable(SamplingFreq, 440, WaveForm::Noise),
};
あとは波形生成部を OscWaveTables を使って波形を読み出すように書き変えます。
-const auto osc = m_oscillator.get(m_time, frequency, static_cast<WaveForm>(m_oscIndex));
+const auto osc = OscWaveTables[m_oscIndex].get(m_time * frequency * 2_pi);
ここまでのコード
差分のみ
コード全体
3.帯域制限付きウェーブテーブルを実装する
ウェーブテーブルができたのでこれで十分かというとそうではありません。ウェーブテーブルを正常に再生できるのは、作成したときと同じ周波数で再生したときのみです。
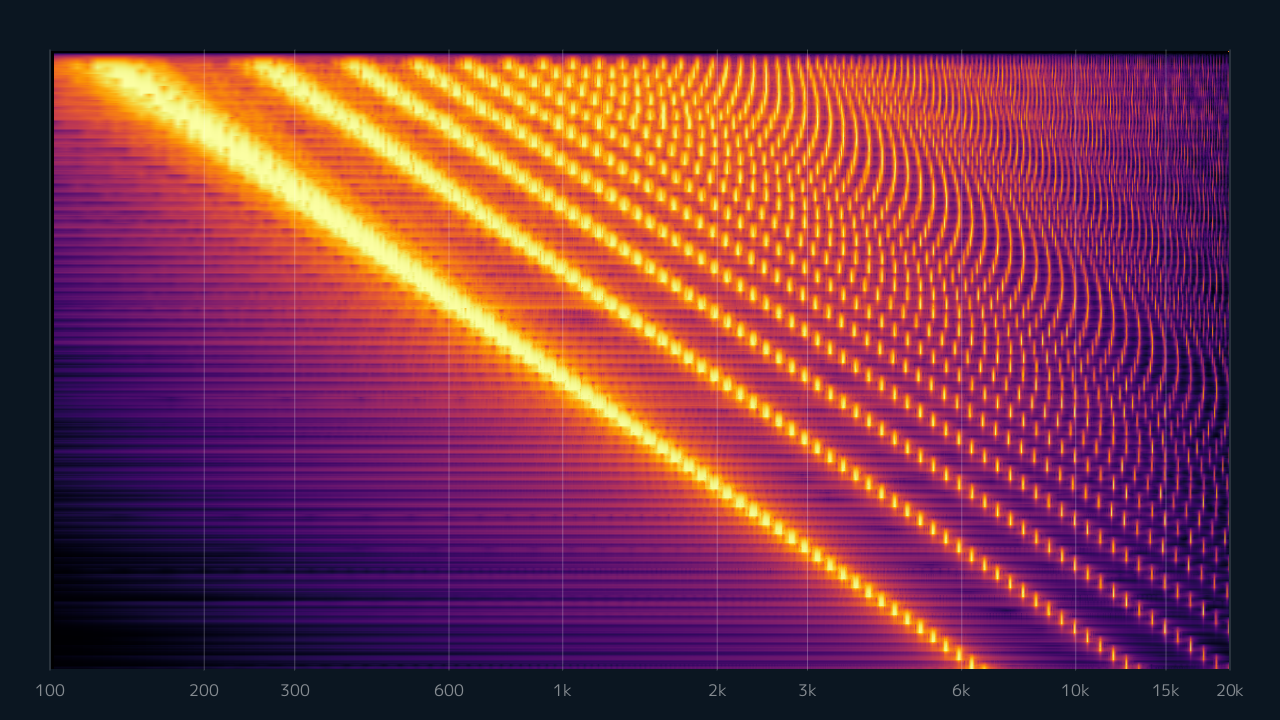
それよりも高い周波数で再生すると、もともとナイキスト周波数の近くにいた高音成分がはみ出るのでエイリアシングが発生します。スペクトログラムを可視化しながら再生周波数を上げていくと、高音から徐々に間隔がずれていく様子を確認できます。
また、作成した周波数よりも低い周波数で再生した場合は、本来あったはずの倍音成分がウェーブテーブルの作成時点でカットされているので、劣化した状態で再生されることになります。
これを解決するために 帯域制限付きウェーブテーブル(Band-limited wavetables) を実装します。これは、周波数を領域に分割して、各領域の周波数ごとに対応したウェーブテーブルを作る方法です。再生する時は、再生周波数に近い周波数で作成したウェーブテーブルから波形を読むようにします。これにより、劣化もノイズも少ない状態で波形を再生することができます。
以下で BandLimitedWaveTables クラスの実装を行います。
static constexpr uint32 MinFreq = 20;
class BandLimitedWaveTables
{
public:
BandLimitedWaveTables(size_t tableCount, size_t waveResolution,
WaveForm waveType);
double get(double x, double freq) const;
private:
double m_minFreqLog = log2(MinFreq);
double m_maxFreqLog = log2(MaxFreq);
Array<OscillatorWavetable> m_waveTables;
Array<float> m_tableFreqs;
};
ウェーブテーブルを生成する
tableCount の数だけ周波数を分割してウェーブテーブルを作成します。音階ごとに等間隔になるように、周波数の分割は対数軸で行います。分割した各周波数について、ウェーブテーブル m_waveTables を追加して、作成時の周波数を m_tableFreqs に記録しておきます。
BandLimitedWaveTables::BandLimitedWaveTables(size_t tableCount,
size_t waveResolution, WaveForm waveType)
{
m_waveTables.reserve(tableCount);
m_tableFreqs.reserve(tableCount);
for (size_t i = 0; i < tableCount; ++i)
{
const double rate = 1.0 * i / tableCount;
const double freq = pow(2, Math::Lerp(m_minFreqLog, m_maxFreqLog, rate));
m_waveTables.emplace_back(waveResolution, freq, waveType);
m_tableFreqs.push_back(static_cast<float>(freq));
}
}
ウェーブテーブルを読み出す
読む時は、作成したウェーブテーブルのリストから std::upper_bound() で再生する周波数に近い要素を検索します。ここで見つかった要素をそのまま使ってもそこまで問題はないのですが、周波数を滑らかに変化させてテーブルの参照が切り替わった時に、急に別の波形に変わると切れ目が目立ってしまう可能性があるので、前後のウェーブテーブルからそれぞれ値を取得して、その間をさらに線形補間で繋げるようにします。
double BandLimitedWaveTables::get(double x, double freq) const
{
const auto nextIt = std::upper_bound(
m_tableFreqs.begin(), m_tableFreqs.end(), freq);
const auto nextIndex = std::distance(m_tableFreqs.begin(), nextIt);
// 作成した周波数の範囲外だったら一番近いテーブルの値をそのまま返す
if (nextIndex == 0)
{
return m_waveTables.front().get(x);
}
if (static_cast<size_t>(nextIndex) == m_tableFreqs.size())
{
return m_waveTables.back().get(x);
}
// freq を挟む二つのウェーブテーブルを使って線形補間する
const auto prevIndex = nextIndex - 1;
const auto rate = Math::InvLerp(
m_tableFreqs[prevIndex], m_tableFreqs[nextIndex], freq);
return Math::Lerp(
m_waveTables[prevIndex].get(x), m_waveTables[nextIndex].get(x), rate);
}
シンセサイザーに組み込む
先ほど作った OscWaveTables を BandLimitedWaveTables で置き換えます。サイン波とノイズはエイリアシングを気にする必要がないのでテーブルの個数は1つで大丈夫です。
-static Array<OscillatorWavetable> OscWaveTables =
-{
- OscillatorWavetable(2048, 440, WaveForm::Saw),
- OscillatorWavetable(2048, 440, WaveForm::Sin),
- OscillatorWavetable(2048, 440, WaveForm::Square),
- OscillatorWavetable(SamplingFreq, 440, WaveForm::Noise),
-};
+static Array<BandLimitedWaveTables> OscWaveTables =
+{
+ BandLimitedWaveTables(80, 2048, WaveForm::Saw),
+ BandLimitedWaveTables(1, 2048, WaveForm::Sin),
+ BandLimitedWaveTables(80, 2048, WaveForm::Square),
+ BandLimitedWaveTables(1, SamplingFreq, WaveForm::Noise),
+};
-const auto osc = OscWaveTables[m_oscIndex].get(m_time * frequency * 2_pi);
+const auto osc = OscWaveTables[m_oscIndex].get(m_time * frequency * 2_pi, frequency);
最後に再びスペクトログラムを表示して、正しく帯域制限ができているかを確認するプログラムを以下に示します。
void Main()
{
Window::Resize(1280, 720);
auto midiDataOpt = LoadMidi(U"C1_B8.mid");
if (!midiDataOpt)
{
// ファイルが見つからない or 読み込みエラー
return;
}
const MidiData& midiData = midiDataOpt.value();
Synthesizer synth;
auto& adsr = synth.adsr();
adsr.attackTime = 0.02;
adsr.releaseTime = 0.02;
Audio audio(RenderWave(synth, midiData));
audio.play();
AudioVisualizer visualizer(Scene::Rect().stretched(-50),
AudioVisualizer::Spectrogram, AudioVisualizer::LogScale);
visualizer.setFreqRange(100, 20000); // [100, 20000] Hz
visualizer.setSplRange(-120, -60); // [-120, -60] dB
while (System::Update())
{
if (KeySpace.down())
{
audio.stop();
synth.clear();
audio = Audio(RenderWave(synth, midiData));
audio.play();
}
visualizer.setInputWave(audio);
visualizer.updateFFT();
visualizer.draw();
}
}
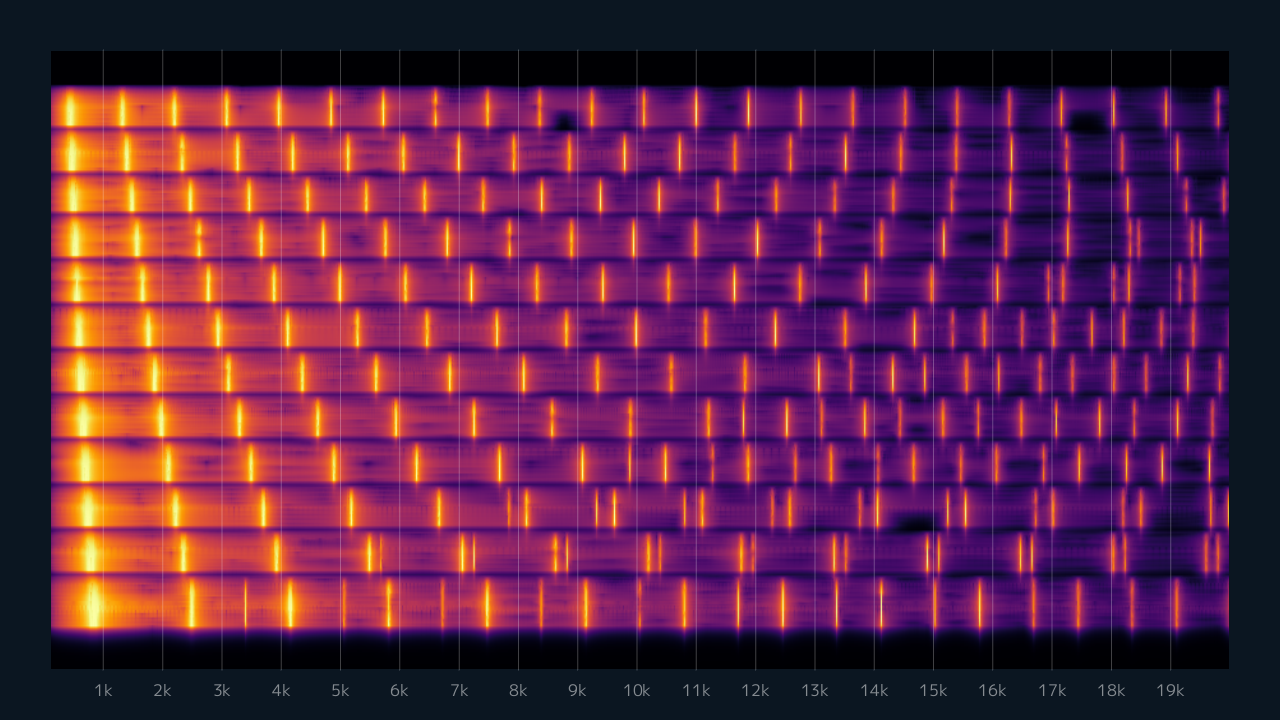
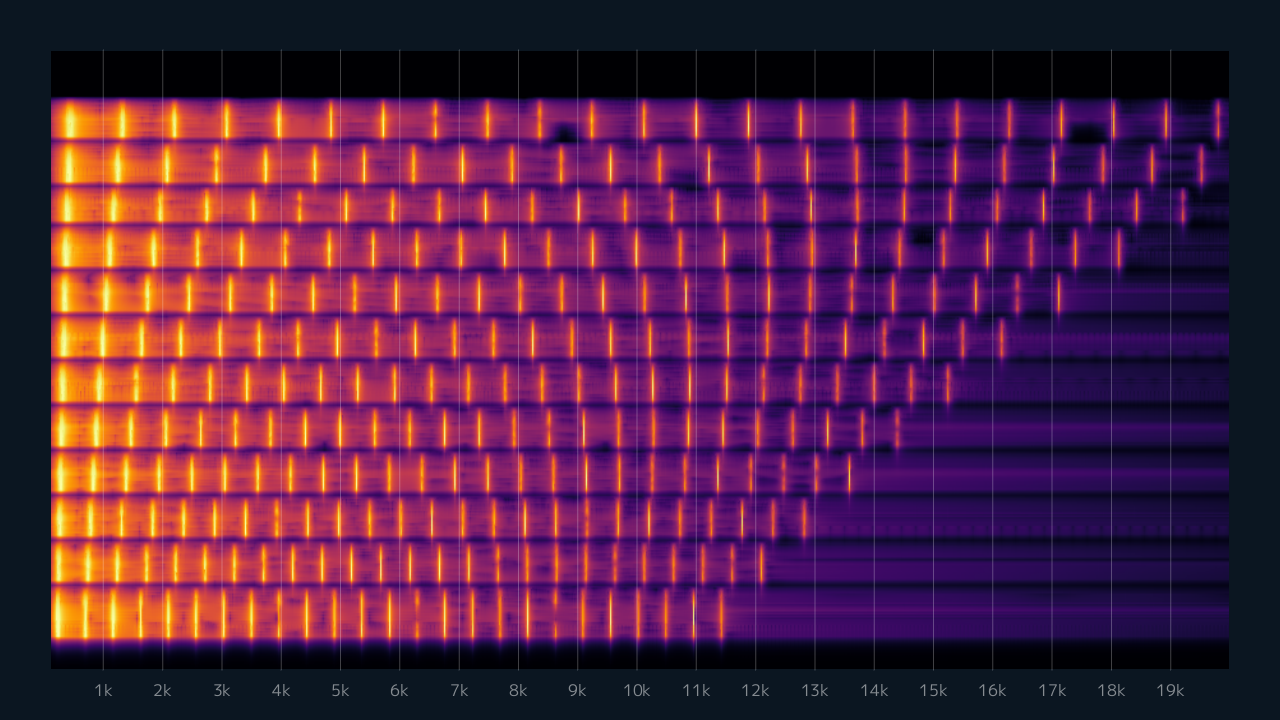
右上の方が詰まっていますが、全体として規則的に出ているのでエイリアシングは起きていないということと、低音でも高周波成分が消えていないので正しいウェーブテーブルを参照できていることがわかると思います。
ここまでのコード
差分のみ
コード全体
4.波形生成をリアルタイムに行う
オシレータをウェーブテーブルに変更したことで波形の生成処理が軽くなったので、Waveクラスを作らずにリアルタイムに生成するようにします。
OpenSiv3D では IAudioStream クラスを継承して getAudio() 関数を実装することで、リアルタイムに再生波形の書き込みを行うことができます。
class AudioRenderer : public IAudioStream
{
void getAudio(float* left, float* right, const size_t samplesToWrite) override
{
for (size_t i = 0; i < samplesToWrite; ++i)
{
const WaveSample waveSample = /* ここで波形を生成する */;
*left++ = waveSample.left;
*right++ = waveSample.right;
}
}
bool hasEnded() override { return false; }
void rewind() override {}
};
AudioRenderer クラスを実装する
RenderWave() 関数の中身をそのままコピーして AudioRenderer クラスを定義します。一つだけ違う点として、RenderWave() 関数は一度の呼び出しで波形を全て生成していましたが、IAudioStream::getAudio()は定期的に少しずつ呼び出されるので、波形を何サンプル目まで生成したかを管理する変数m_readMIDIPosを追加しています。
class AudioRenderer : public IAudioStream
{
public:
void setMidiData(const MidiData& midiData)
{
m_midiData = midiData;
}
void updateGUI(Vec2& pos)
{
m_synth.updateGUI(pos);
}
private:
void getAudio(float* left, float* right, const size_t samplesToWrite) override
{
for (size_t i = 0; i < samplesToWrite; ++i)
{
const double currentTime = 1.0 * m_readMIDIPos / SamplingFreq;
const double nextTime = 1.0 * (m_readMIDIPos + 1) / SamplingFreq;
...
// RenderWave()の中身をコピー
...
const auto waveSample = m_synth.renderSample();
*left++ = waveSample.left;
*right++ = waveSample.right;
++m_readMIDIPos;
}
}
bool hasEnded() override { return false; }
void rewind() override {}
Synthesizer m_synth;
MidiData m_midiData;
size_t m_readMIDIPos = 0;
};
Main関数
Main関数では、作ったAudioRendererをAudioクラスに渡して再生開始します。そうするとAudioが内部で勝手に getAudio()関数を呼び出してストリーム再生するようになります。
これで音を聞きながらパラメータを調整することができるようになりました。
void Main()
{
auto midiDataOpt = LoadMidi(U"example/midi/test.mid");
if (!midiDataOpt)
{
// ファイルが見つからない or 読み込みエラー
return;
}
std::shared_ptr<AudioRenderer> audioStream = std::make_shared<AudioRenderer>();
audioStream->setMidiData(midiDataOpt.value());
Audio audio(audioStream);
audio.play();
while (System::Update())
{
Vec2 pos(20, 20 - SliderHeight);
audioStream->updateGUI(pos);
}
}
ここまでのコード
差分のみ
コード全体
5.パフォーマンスをもう少し最適化する
リアルタイム再生は実装できましたが、まだ無駄な処理が多いので音が重なると途切れてしまいます。そこで、プロファイルを取りながら特に重い部分の処理をいくつか削りました。以下にここで行った最適化の内容を書いておきます。
剰余計算を無くす
OscillatorWaveTable でウェーブテーブルを読む時に使っていたfmodがボトルネックであることがわかりました。
const float indexFloat = fmod(x * resolution / 2_pi, resolution);
これを取り除くためにオシレータの入力は $[0,2\pi]$ の範囲に決め打ち、以下のように修正しました。
double get(double x) const
{
- const size_t resolution = m_wave.size();
- const double indexFloat = fmod(x * resolution / 2_pi, resolution);
- const int indexInt = static_cast<int>(indexFloat);
- const double rate = indexFloat - indexInt;
- return Math::Lerp(m_wave[indexInt], m_wave[(indexInt + 1) % resolution], rate);
+ auto indexFloat = x * m_xToIndex;
+ auto prevIndex = static_cast<size_t>(indexFloat);
+ if (m_wave.size() == prevIndex)
+ {
+ prevIndex -= m_wave.size();
+ indexFloat -= m_wave.size();
+ }
+ auto nextIndex = prevIndex + 1;
+ if (m_wave.size() == nextIndex)
+ {
+ nextIndex = 0;
+ }
+ const auto x01 = indexFloat - prevIndex;
+ return Math::Lerp(m_wave[prevIndex], m_wave[nextIndex], x01);
}
呼びだす側もこれに合わせてxが $2\pi$ を超えないように修正する必要があります。このために時刻をSynthesizerクラスのm_timeで管理していたのをやめて、ノートごとの位相変数として持たせることにしました。
struct NoteState
{
+ double m_phase = 0;
float m_velocity;
EnvGenerator m_envelope;
};
波形生成部では、1サンプルごとに各ノートの位相を deltaT * frequency * 2_pi だけ進めていきます。1サンプルで進む位相の大きさは最大でも $\pi$ なので、位相を更新したときに $2\pi$ を超えていたら単に $2\pi$ 引くことで $[0,2\pi]$ の範囲に収まります。
for (auto& [noteNumber, noteState] : m_noteState)
{
const auto envLevel = noteState.m_envelope.currentLevel() * noteState.m_velocity;
const auto frequency = NoteNumberToFrequency(noteNumber);
- const auto osc = OscWaveTables[m_oscIndex].get(m_time * frequency * 2_pi, frequency);
+ const auto osc = OscWaveTables[m_oscIndex].get(noteState.m_phase, frequency);
+ noteState.m_phase += deltaT * frequency * 2_pi;
+ if (Math::TwoPi < noteState.m_phase)
+ {
+ noteState.m_phase -= Math::TwoPi;
+ }
const auto w = static_cast<float>(osc * envLevel);
sample.left += w;
sample.right += w;
}
-m_time += deltaT;
ウェーブテーブルの探索処理を削る
次に重かったのが BandLimitedWaveTables で、再生周波数から適切なウェーブテーブルを探索する箇所でした。
auto upperIt = std::upper_bound(freqs.begin(), freqs.end(), freq);
二分探索でも重いようなので、インデックスの配列を作ってウェーブテーブル作成と同時にstd::upper_bound()の結果も保存するようにしました。
class BandLimitedWaveTables
{
...
+ Array<uint32> m_indices;
+ double m_freqToIndex = 0;
};
BandLimitedWaveTables::BandLimitedWaveTables(size_t tableCount, size_t waveResolution, WaveForm waveType)
{
m_waveTables.reserve(tableCount);
m_tableFreqs.reserve(tableCount);
for (size_t i = 0; i < tableCount; ++i)
{
const double rate = 1.0 * i / tableCount;
const double freq = pow(2, Math::Lerp(m_minFreqLog, m_maxFreqLog, rate));
m_waveTables.emplace_back(waveResolution, freq, waveType);
m_tableFreqs.push_back(static_cast<float>(freq));
}
+ {
+ m_indices.resize(2048);
+ m_freqToIndex = m_indices.size() / (1.0 * MaxFreq);
+ for (int i = 0; i < m_indices.size(); ++i)
+ {
+ const float freq = static_cast<float>(i / m_freqToIndex);
+ const auto nextIt = std::upper_bound(m_tableFreqs.begin(), m_tableFreqs.end(), freq);
+ m_indices[i] = static_cast<uint32>(nextIt - m_tableFreqs.begin());
+ }
+ }
}
これを使って、ウェーブテーブル参照時の探索処理を配列の参照に置き換えました。
double BandLimitedWaveTables::get(double x, double freq) const
{
- const auto nextIt = std::upper_bound(m_tableFreqs.begin(), m_tableFreqs.end(), freq);
- const auto nextIndex = std::distance(m_tableFreqs.begin(), nextIt);
+ const auto nextIndex = m_indices[static_cast<int>(freq * m_freqToIndex)];
...
}
バッファリングを実装する
ここまでである程度軽くはなりましたが、それでも複数並べたりすると同時発音数が多くなる瞬間に負荷が増えるため音が途切れてしまいます。そこで、生成した波形を即座に再生するのはやめて0.1秒ほどバッファに溜めることにしました。これで間に合わないということはほぼ無くなるので、安定して動くようになりました。
AudioRenderer の変更箇所
具体的な実装について説明します。まずバッファ用の変数と、読み書きのサンプル位置管理用の変数を追加します。また、バッファ書き込みが完了していることを示すbufferCompleted()関数も追加します。
class AudioRenderer : public IAudioStream
{
public:
+ AudioRenderer()
+ {
+ // 100ms分のバッファを確保する
+ const size_t bufferSize = SamplingFreq / 10;
+ m_buffer.resize(bufferSize);
+ }
+
+ bool bufferCompleted() const
+ {
+ return m_bufferReadPos + m_buffer.size() - 1 < m_bufferWritePos;
+ }
...
+ Array<WaveSample> m_buffer; // 生成した波形を保存するバッファ
+ size_t m_bufferReadPos = 0; // 読み終わった波形のサンプル位置
+ size_t m_bufferWritePos = 0; // 書き終わった波形のサンプル位置
};
そしてgetAudioではバッファの現在の位置から波形を読み込んでそのまま流すだけにします。
void AudioRenderer::getAudio(float* left, float* right,
const size_t samplesToWrite) override
{
for (size_t i = 0; i < samplesToWrite; ++i)
{
const auto& readSample = m_buffer[(m_bufferReadPos + i) % m_buffer.size()];
*left++ = readSample.left;
*right++ = readSample.right;
}
m_bufferReadPos += samplesToWrite;
}
波形生成処理はbufferSample()関数を新たに追加してそちらに移しました。この関数は波形を1サンプル生成してバッファに書き込みます。MIDIイベントの読み込み位置はm_readMIDIPosで管理し、波形の書き込み位置はm_bufferWritePosで管理します。MIDIをループ再生やリスタートする時は m_readMIDIPos だけリセットするようにします。
void AudioRenderer::bufferSample()
{
const double currentTime = 1.0 * m_readMIDIPos / SamplingFreq;
const double nextTime = 1.0 * (m_readMIDIPos + 1) / SamplingFreq;
...
// MIDI イベント更新処理
...
const size_t writeIndex = m_bufferWritePos % m_buffer.size();
m_buffer[writeIndex] = m_synth.renderSample();
++m_bufferWritePos;
++m_readMIDIPos;
}
Main関数の変更箇所
Main関数では、バッファへの書き込み専用のレンダースレッドを新たに用意します。レンダースレッドでは書き込みが完了したかを常にチェックしながら、メインループを抜けるまで波形を生成し続けるようにします。
void Main()
{
auto midiDataOpt = LoadMidi(U"example/midi/test.mid");
if (!midiDataOpt)
{
// ファイルが見つからない or 読み込みエラー
return;
}
std::shared_ptr<AudioRenderer> audioStream = std::make_shared<AudioRenderer>();
audioStream->setMidiData(midiDataOpt.value());
+ bool isRunning = true;
+
+ auto renderUpdate = [&]()
+ {
+ while (isRunning)
+ {
+ while (!audioStream->bufferCompleted())
+ {
+ audioStream->bufferSample();
+ }
+
+ std::this_thread::sleep_for(std::chrono::milliseconds(1));
+ }
+ };
+
+ std::thread audioRenderThread(renderUpdate);
Audio audio(audioStream);
audio.play();
while (System::Update())
{
Vec2 pos(20, 20 - SliderHeight);
audioStream->updateGUI(pos);
}
+ isRunning = false;
+ audioRenderThread.join();
}
ここまでのコード
差分のみ
コード全体
参考資料
次回