[機械学習] 2.1 教師あり学習 (ロジスティック回帰)

導入

以前の記事でAI技術や機械学習についてどのようなものがあるのか,世間的にどのような立ち位置にあるのかなどの全体感について執筆させていただきました.

今回は縁あって技術書を読む機会があり, より踏み込んだ内容について少し分かったので自分用にまとめ.

復習ですが, 機械学習には大きく3つの分野に分かれており

• 教師あり学習(Supervised Learning)
• 教師なし学習(Unsupervised Learning)
• 強化学習(Reinforcement Learning)
  に大別されます.

本記事では中でも 教師あり学習 について考え方やアルゴリズムの内容などに触れていきたいと思います。

教師あり学習の考え方

例えばあなたは製造ラインの生産管理を任せられているとします.
そのラインでは一定程度不良品が出てきてしまいます。歩留まりの原因やお客さんに迷惑をかけてしまったりと大変困ったことです.
何とかしたいところですが人の目で判断するには当然限界があります. そこで教師あり学習の出番です!!
蓄積されたカメラの画像やセンサーの情報から「正常品」「不良品」が自動的に分かったらとても助かりますよね？

他にも過去の販売データや季節要因などをもとに「来月の売上」が分かると在庫や仕入れの計画だったりと助かるかなと思います.

このように 過去に蓄積されたデータから法則を見つけ出し, 未知のデータに対しても判断を行うこと が教師あり学習の大目標です.

分類タスクと回帰タスク

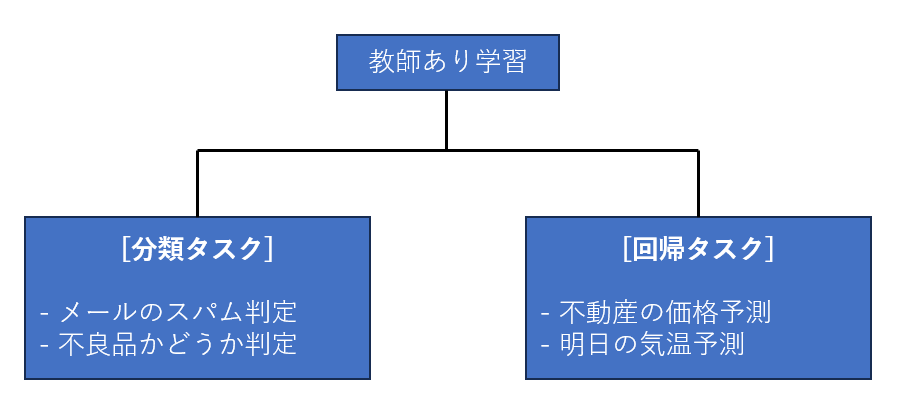
教師あり学習にはさらに「分類タスク(Classification)」と「回帰タスク(Regression)」という種類に大きく分かれます. (機械学習の世界では解くべき課題や問題の種類を「タスク」と呼びます)

• 分類タスク : メールのスパム判定や動物の種類のような カテゴリ(ラベル) を予測する
• 回帰タスク : 売上や気温のような 数値 を予測する
  といったような違いがあります.

つまるところ, 分類タスクは離散値の予測で回帰タスクは連続値 の予測といった考え方ができますね.
先ほどの例で言うと不良品かどうかの予測は分類タスクで, 来月の売り上げ予測は回帰タスクということになります.

分類タスク

では、さっそく教師あり学習のうちの1タスクである分類タスクについて解説を行っていこうと思います。
分類タスクは「このメールは迷惑メールであるのか？」といったようなYes/Noで答えられるような 2クラス分類 と, 3種類以上のクラス分類を対象とした 多クラス分類 にしばしば分けられます.

本記事では2クラス分類の手法として良く用いられる ロジスティック回帰 の理論部分と実装についてまとめようと思います.

前準備

- ライブラリのインポート

機械学習の実装には, scikit-learn というライブラリがとても有用です.このライブラリには実験用に用いるデータセットや様々な学習アルゴリズムなどが含まれており, pythonで機械学習を行うのに一般的なライブラリとなります.
他にも描画用や算術用ライブラリなどをインストールしましょう.

terminal

pip install scikit-learn
pip install numpy
pip install pandas
pip install matplotlib

- データセットの準備

実際にコードを見ながらどのようなアルゴリズムなのか解説を行っていこうと思います.
その前に前準備として, データセットの準備と描画用の関数を用意します.

Prepare Train Data & Test Data

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split

# 分類タスクで用いるデータセット. 人工的なデータを生成
X, y = make_classification(n_samples = 400, n_features = 2, n_redundant = 0, n_informative = 2, n_clusters_per_class = 1, random_state = 42)

# 生成したデータセットを「学習データ(*_train)」と「テストデータ(*_test)」に分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 42)

コメントにもありますが本記事ではmake_classificationという関数を使って人工的なデータセット生成します.

• n_samples : データのサンプル数
• n_features : 特徴量 (今回は2値分類なので2クラス)
• n_redundant, n_informative : 詳しくは書きませんが簡単に言うと分割のしやすさ
• n_clusters_per_class : クラスタの数. 今回は1で設定しているのでデータ全体を遠くから見たら1つの塊のように見える. (=データの塊の数)
• random_state : データ生成のための乱数シード値. 別に0でも123とかでもいいが, 機械学習の界隈ではシード値として42を使う文化がある. (元ネタは「銀河ヒッチハイク・ガイド」の「生命、宇宙、そしてすべての答え」は “42” というギャグ的な答えから)

生成されたデータセットを学習データ と テストデータ に分割するのが後半部分のスクリプトになります.

• test_size : データセットの何割をテストデータに割り振るか. 一般的に8割を学習データ, 2割をテストデータに用いるのが多いようです.
• random_state : 配列をシャッフルする際の乱数シード値. 学習データが偏ることを避けるためにシャッフルします.

- 描画用の関数

drawPredictResult

def drawPredictResult(X_test, y_pred, model):
    interval = 0.02
    x_min, x_max = X_test[:, 0].min() - 1, X_test[:, 0].max() + 1
    y_min, y_max = X_test[:, 1].min() - 1, X_test[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, interval),
                        np.arange(y_min, y_max, interval))

    Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    
    fig, ax = plt.subplots(nrows = 1, ncols = 1, figsize = (8, 6))
    ax.grid(True)
    ax.set_title(model.__class__.__name__)
    ax.set_xlabel("Feature 1")
    ax.set_ylabel("Feature 2")
    ax.contourf(xx, yy, Z, cmap = plt.cm.coolwarm, alpha = 0.4)
    ax.scatter(X_test[:, 0], X_test[:, 1], c = y_pred, cmap = plt.cm.coolwarm, edgecolor = "k")
    plt.show()

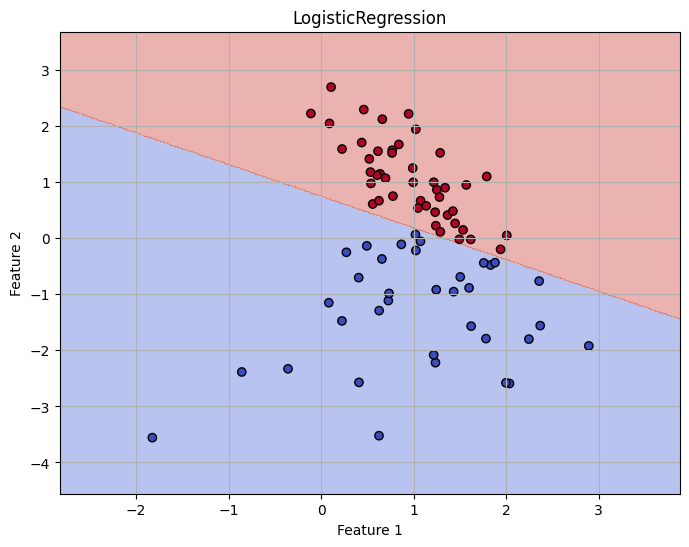
この関数にテストデータ, 予測ラベル結果とフィット後のmodelを引数に入れれば予測結果と決定境界を描画することができます。

決定境界 : クラスを分類する際に、選り分けるための境界線(切れ目)のこと
手法によって線形だったり非線形な境界になったりします

ロジスティック回帰 <理論>

学習について

分類の話をするぞ、といったのにいきなり回帰？と思う方も中にはいらっしゃるかもです。
名前に回帰とありますが実際は分類の手法となります。なんでこんな名前つけたんだろ？

ロジスティック回帰では2値分類の問題を扱います.
以下のような式を考えてみましょう:

p(Y = 1 | X) = \pi(X)

上式を日本語で言うと特徴量Xが与えられたときにクラス1へ分類される条件付き確率という意味になります.
これを線型結合で表したいのですが,単純に

\pi(X) = w \top X + b

とすると確率の値域(0 ~ 1)を超えてしまうことが充分考えられますので予測値としては不適切な感じがしますね.
そこで「リンク関数」と言うものが必要となります.

リンク関数は確率 $ \pi $ (0 ~ 1)を実数(-∞ ~ ∞)に写像する関数です. ロジスティック回帰においてはこのリンク関数としてオッズ比の対数を取った ロジット関数 を適用します.

ロジット関数は以下のような式で定義されています.

    \rm{logit}(\pi) = \ln(\frac{\pi}{1-\pi})

上式を一言でいえば, 事象pが起こる確率÷起こらない確率です.

で,ロジスティック関数ではこのロジット関数が $ w \top X + b $ とイコールであるとすることで, 線形予測の結果を確率空間にマッピングできるようにします.

\ln(\frac{\pi}{1-\pi}) = b + w_1x_1 + w_2x_2 \dots + w_kx_k

そして, $ \pi $に関して逆関数を考えることで線形予測値の確率変換値が得られます.

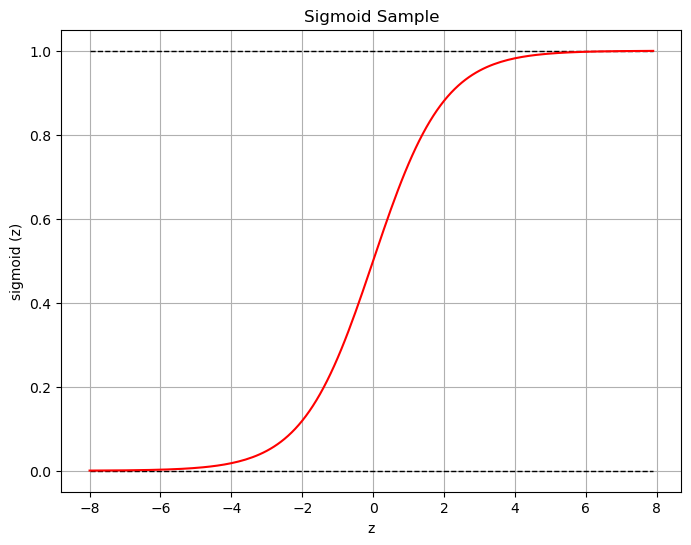
\pi = \frac{1}{1 + e^{-(b + w_1x_1 + w_2x_2 \dots + w_kx_k)}}

この時の関数をシグモイド関数といい, 機械学習の文脈ではたくさん耳にすると思います.

入力された値を0 ~ 1へとスケーリングされていることが見て取れますね.

次に考えることは 誤差関数 です.最適化の文脈では目的関数とか呼ばれたりしますが, よく使われるのは 平均2乗誤差(Square Root Mean Error) ですね.

L = \sum_{n = 1}^{k} \sqrt{\frac{1}{2}(y - \hat{y})^2}

しかし,今回のケースでは適切ではないと思われます.理由として

1. シグモイド関数と合わせて考えると勾配が小さくなるために学習が進まないケースを考えられます.(勾配消失）
2. 確率の予測としては適していない

などの理由でSMREは使いません.
代わりに 対数尤度 を用います. 以下の式が 尤度関数 となります.

L = \prod_{n=1}^{k} = \hat{y}_i^{y_i} \cdot (1-\hat{y_i})^{1-y_i}

正解ラベル $y_i = 1$ のときは陽性の予測ラベル $\hat{y}_i$ が残り
$y_i = 0$ のときは陰性の予測ラベル $1 - \hat{y}_i$が残るように作られています.
-> これにより1 or 0 どちらが出たかを一つの式で表現できる

そしてこの尤度関数の対数を取ったものを対数尤度と言います.
以下のような式になります.

\ln{L} = \sum_{i = 1}^{k}(y_i)\ln{\hat{y}_i} + (1-y_i)\ln{(1-\hat{y}_i)}

(logを取っているので総乗が総和になってます)
また, 最適化問題では損失を最小化させるのが一般的なので, 符号をひっくり返します.
これを 交差エントロピー損失 といい正解ラベルとの誤差を表します.

J = -\sum_{i = 1}^{k}(y_i)\ln{\hat{y}_i} + (1-y_i)\ln{(1-\hat{y}_i)}

そして, 勾配を求めて重みを更新していくこととなります.
ちなみに勾配はシンプルにチェーンルールで求めることができます.
1サンプルデータの損失を j として考えると

\frac{\partial j}{\partial w} = \frac{\partial j}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial \pi} \cdot \frac{\partial \pi}{\partial w}

それぞれ

\begin{align}
 \frac{\partial j}{\partial \hat{y}} &= -(\frac{y}{\hat{y}} - \frac{1-y}{1-\hat{y}})  \\
 \frac{\partial \hat{y}}{\partial \pi} & = \hat{y}(1-\hat{y})\\
 \frac{\partial \pi}{\partial w} &= x 
\end{align}
 \\

です. 以上の式から意外とシンプルな形になります.

\frac{\partial j}{\partial w} = (\hat{y} - y) \cdot x

データ全体に対する勾配は

\Delta J = \frac{1}{k} \sum_{i=1}^{k}(\hat{y}_i - y_i) \cdot x_i

これが損失関数に対する重みベクトルの勾配となります.

これをもって最急降下法でパラメータを更新します.

w \leftarrow w - \eta \cdot\Delta J

ここで$\eta$は 学習率(learning rate) です. 小さすぎるとステップ数が小さいということになるので学習までに時間がかかります. 一方で, 大きすぎると最適解を見逃してしまう可能性があります.

学習についてまとめ

ばーっと数式などを言ってしまいましたが, いったんここでまとめましょう.
結局以下のような表にまとめられます.

項目	内容
モデル	$\hat{y}_i = \frac{1}{1 + e^{-(b + w_1x_1 + w_2x_2 \dots + w_kx_k)}}$
損失関数	$ J = -\sum_{i = 1}^{k}(y_i)\ln{\hat{y}_i} + (1-y_i)\ln{(1-\hat{y}_i)} $
勾配	$ \Delta J = \frac{1}{k} \sum_{i=1}^{k}(\hat{y}_i - y_i) \cdot x_i $
重みの学習法	最急降下法 $ w \leftarrow w - \eta \cdot\Delta J$

予測について

学習が終わった後に重みが得られた状態で入力に対してどう予測するのか?という話に入っていきます.
学習済みのモデルとして重みwとバイアスbがすでに既知の状態です.
そして, 入力された特徴量をモデルに入力した結果を閾値により判断されます.

pred\_class =　\left\{ \begin{array}{ll}
1 & \quad \hat{y} \geq 0.5 \\
0 & \quad \hat{y} < 0.5
\end{array}
\right.

少し具体的な数値例を持ってきました.

• 学習済みの重み

\begin{align}
w &= [2.0, -1.0] \\
b &= -0.5
\end{align}

• 入力データ

x = [1.0, 2.0]

step 1. 線形結合$\pi$を計算

\pi = w\top x + b = 2.0 \cdot 1.0 + (-1.0) \cdot 2.0 + (-0.5) = -0.5

step 2. シグモイド関数で確率空間へ

\hat{y} = \frac{1}{1+e^{-(-0.5)}} \approx 0.3375

step 3. 閾値0.5と比較
$\hat{y} < 0.5$なのでこの特徴量だと予測クラスは0

といった流れになります.

ロジスティック回帰 <実装>

理論部でなかなか難しいことを書いていましたが、実装自体は scikit-learn ライブラリのおかげでとても簡単です.

LogisticRegression

from sklearn.linear_model import LogisticRegression

model = LogisticRegression()      # モデルのインスタンス
model.fit(X_train, y_train)　　   # トレーニングデータによるモデル学習
y_pred = model.predict(X_test)    # テストデータにモデルを適用し予測を実施

実際に結果を描画してみましょう.

drawGraph

drawPredictResult(X_test, y_pred, model)