高次元空間中の正規分布は超球面状に分布する

この記事は古川研究室 Workout_calendar 5日目の記事です。
（注：2021/02/08に「付録」の誤りを修正し、参考になりそうな文献を追記しました）

忙しい人へアニメで説明

多変量正規分布の次元をどんどん上げていくと、こうなります。

最終的には超球面になります。

はじめに

正規分布（ガウス分布）と聞いて、皆さんどんな「形」を思い浮かべるでしょうか？おそらく、こんな形を思い浮かべるのではないでしょうか

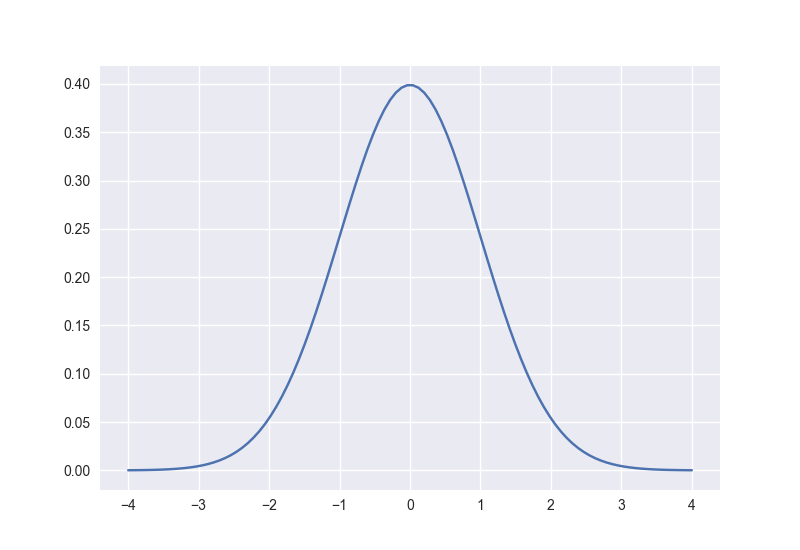
これは標準正規分布$p(x)=\frac{1}{\sqrt{2\pi}}\exp(-\frac{1}{2}x^2)$のグラフそのものです。正規分布を知ってる人なら、きっとこの形を思い浮かべますよね。では2次元の正規分布ではどうでしょう？

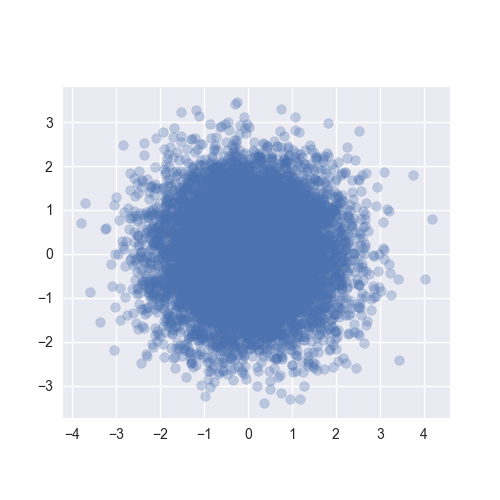
これは2次元の標準正規分布からのサンプル点を図示したものです。まぁこんな感じですよね。同じように3次元も見てみましょう。

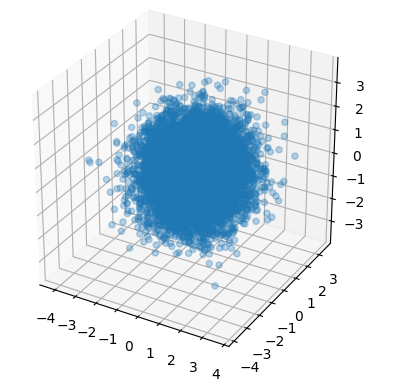
というように次元の違いはあれど、「中心（平均）あたりが密で、そこから離れるほど疎になるような分布」をイメージするのではないでしょうか？

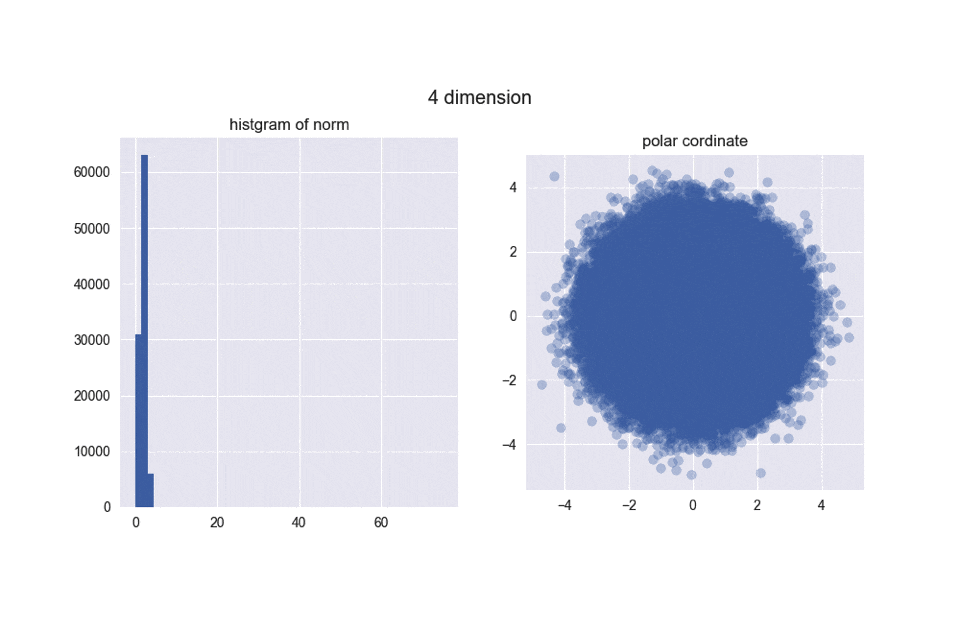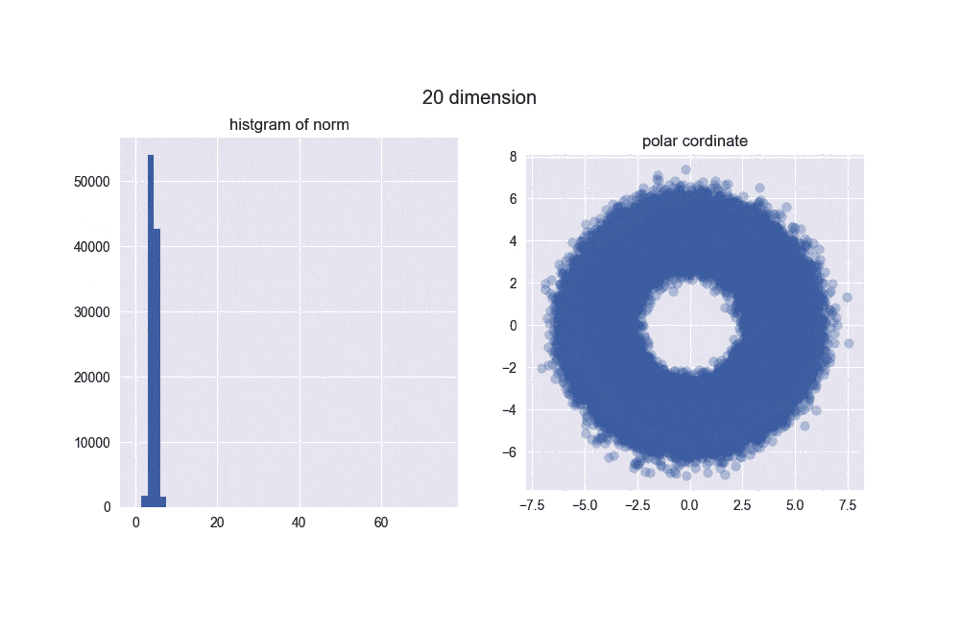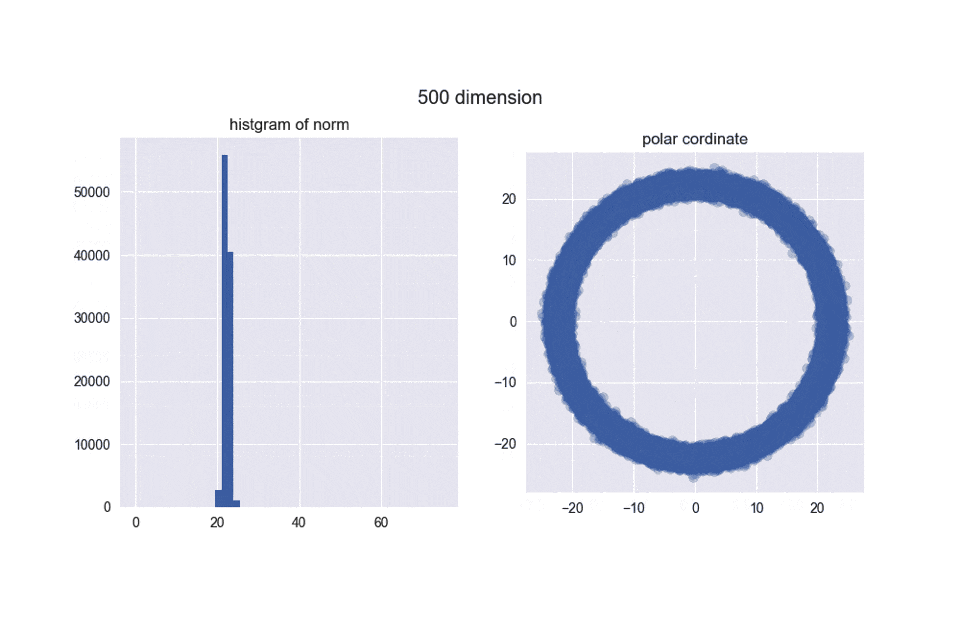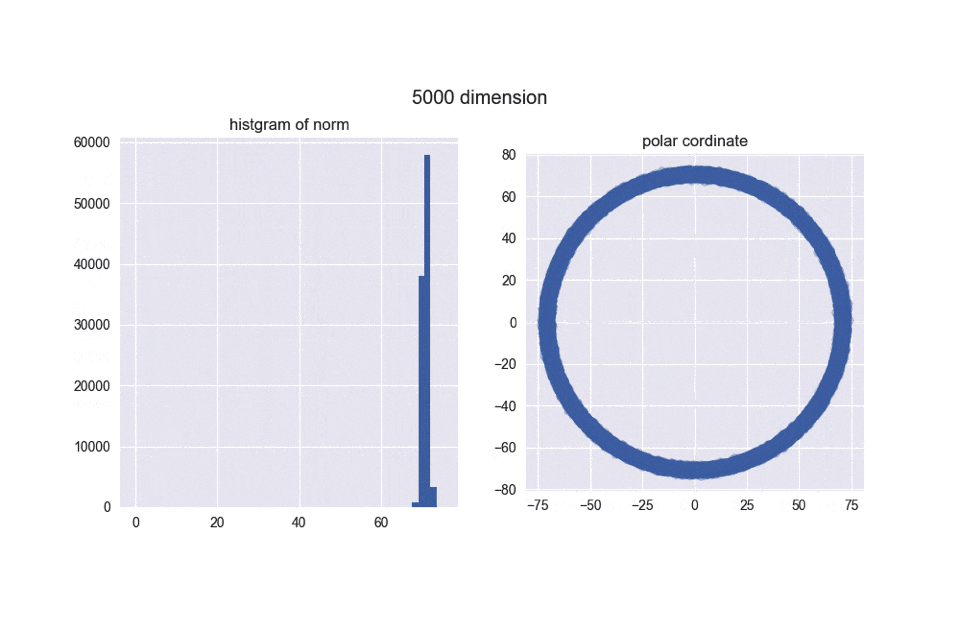
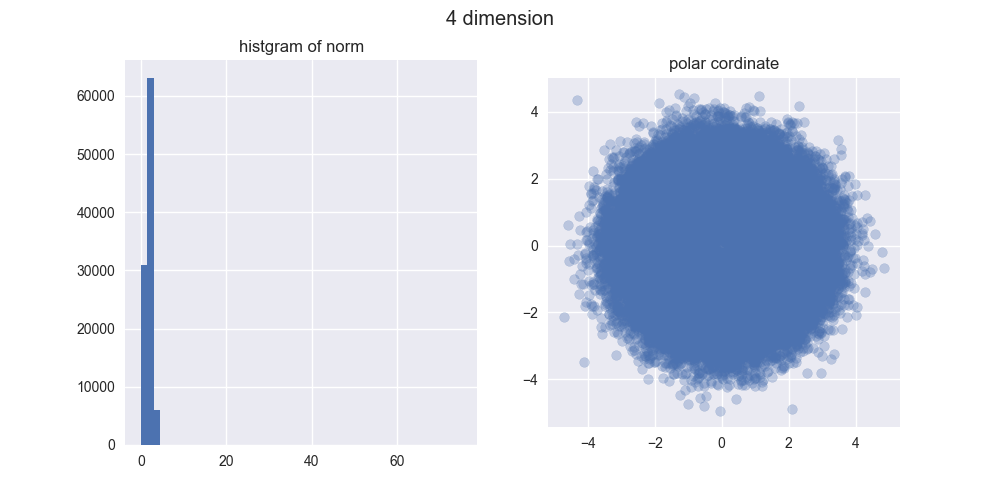
では、もっともっと次元を高くするとどうなるでしょう？「え？同じような感じじゃないの？」と思っている方にとって衝撃的な事実をお知らせしなければなりません。以下の図¹をご覧ください。

左は先ほども示した2次元の正規分布です。右は超高次元空間中の正規分布のイメージ図です。実は球面状に（厳密には超球面状に）分布します。は？何言ってんの？って感じですよね。これからなぜそうなるのか説明していきます。

なぜ超球面状になるのか

いま以下のような多変量正規分布を考えましょう。

$$p(\mathbf{x})=\mathcal{N}(\mathbf{x}|\mathbf{0},\mathbf{I}_n)$$

ただし$\mathbf{x}\in\mathbb{R}^n$で、簡単のために平均は原点、共分散行列を$n\times n$の単位行列$\mathbf{I}_n$とします。

ここで、ノルム$||\mathbf{x}||$の期待値$E(||\mathbf{x}||)$は、以下のようになります²。

シミュレーションで確かめてみた

それでも半信半疑な方もいると思うので、シミュレーションで確かめてみます。実際に多変量正規分布から大量にサンプリングを行い、なんとかそれを可視化することにトライします。具体的には以下の2つの図を見ます。

• ノルムのヒストグラム
• ノルムと角度を用いた極座標表示

後者は、得られたサンプル$\mathbf{x}$に対して、極座標$(r,\theta)$を以下のように計算し、それをプロットします。
$$
\begin{align}
r&=||\mathbf{x}||\
\theta&\sim U(-\pi,\pi)
\end{align}
$$
角度$\theta$に関しては、まぁ一様だろうということで一様な乱数で生成させています（ここの厳密性に関してはご愛嬌ということで）。
それでは、次元をどんどん大きくした時、この2つのグラフがどのように変わるか見ていきたいと思います。実装はgithubで公開しています。たくさん載っけているのでヌルヌルスクロールしちゃってください。

4次元

よく知ってるガウスって感じですね

5次元

真ん中に小さな穴が空きました

10次元

おぉ
50次元

どんどん広がってきました
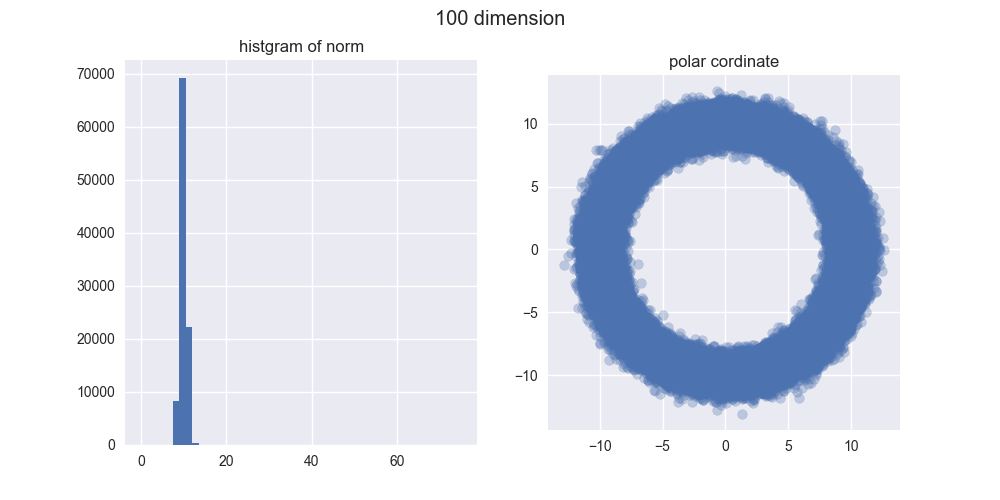
100次元

200次元

500次元

もやっぽかったのがだんだんクリアになってきましたかね？
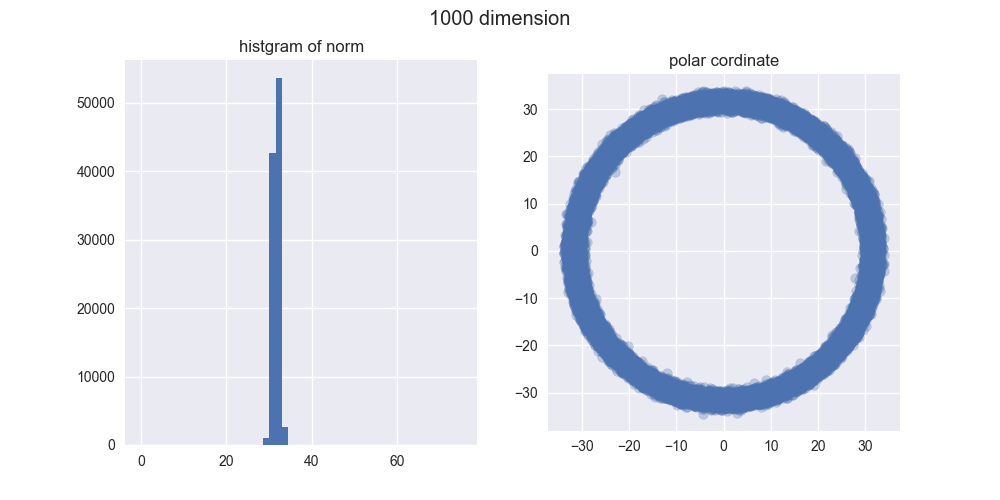
1000次元

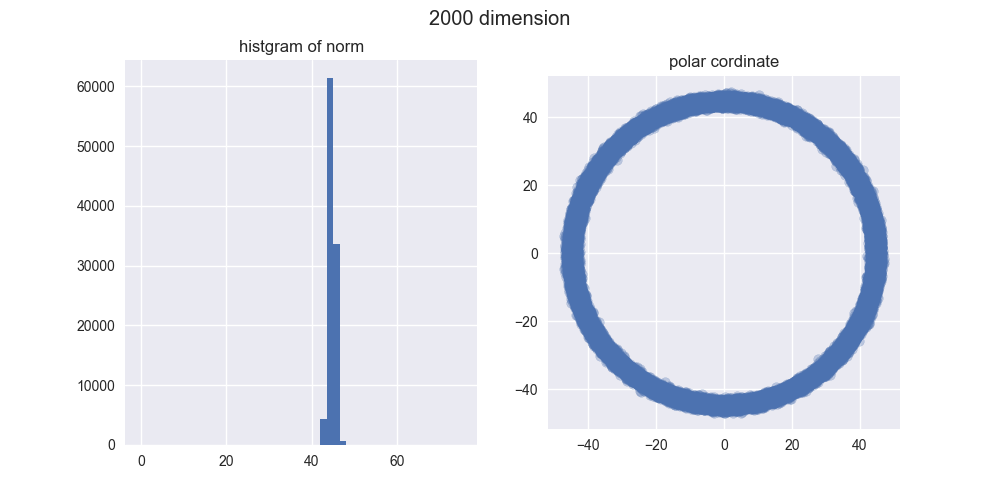
2000次元

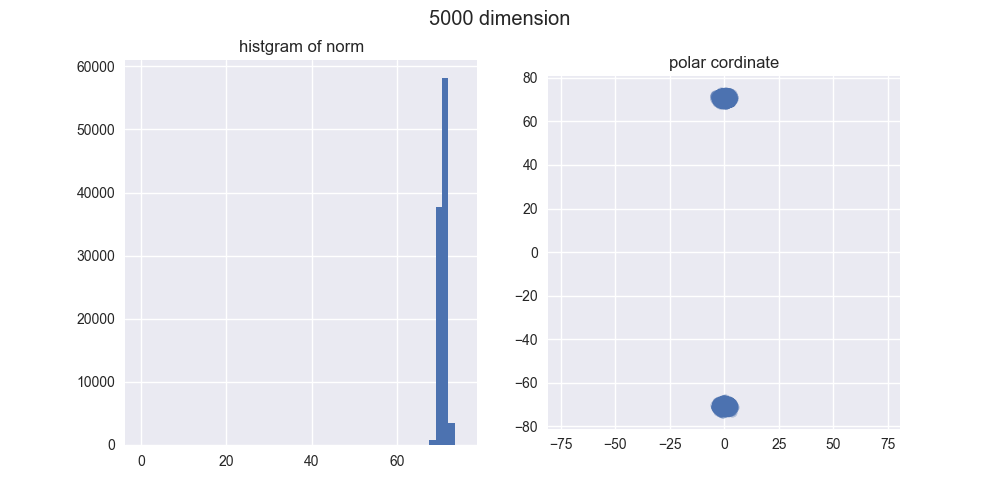
5000次元

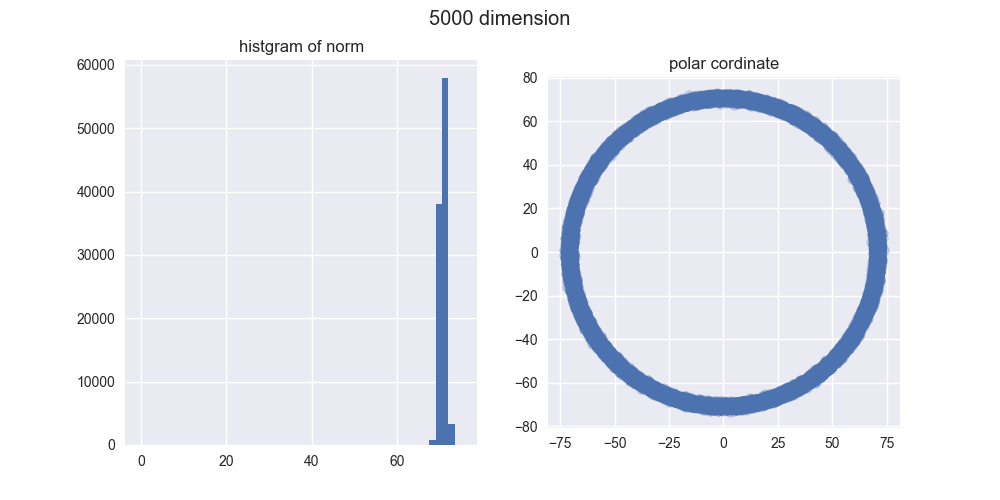
私のPCメモリの都合上、5000次元程度が限界でした。。。
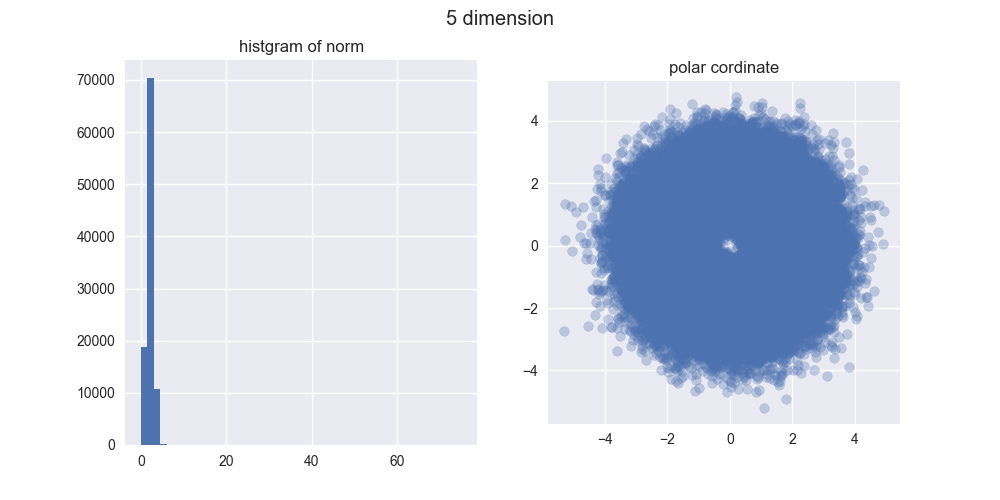
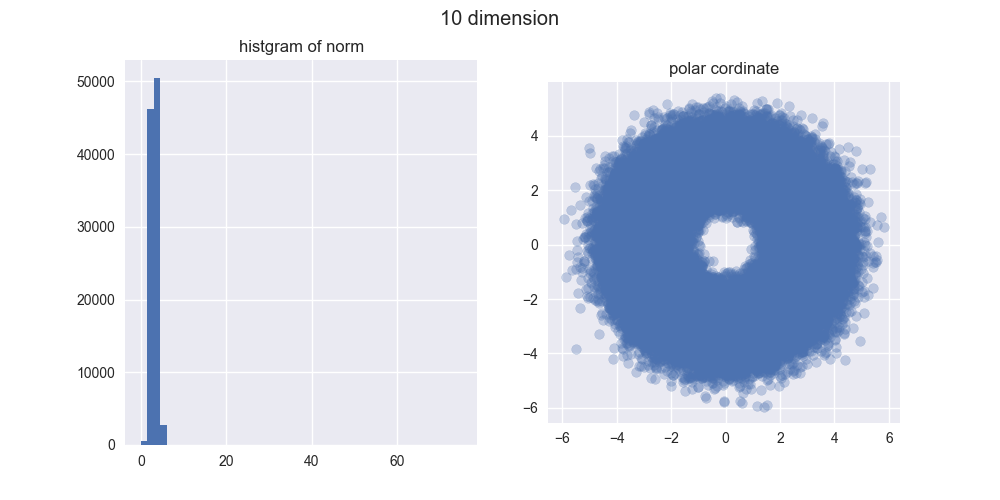
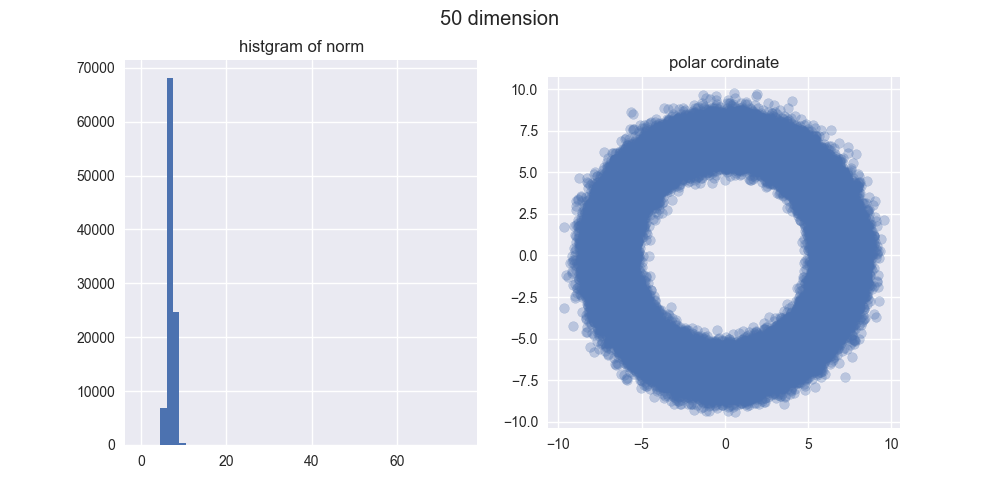
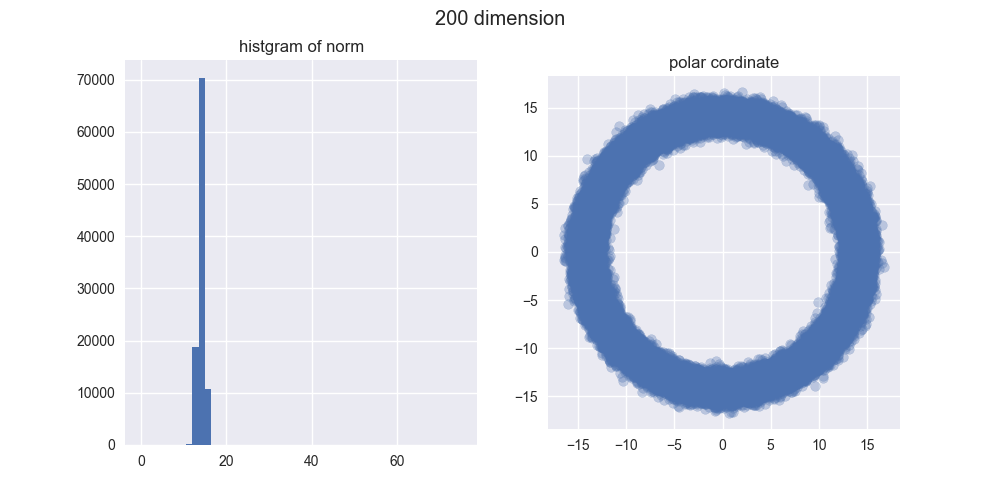
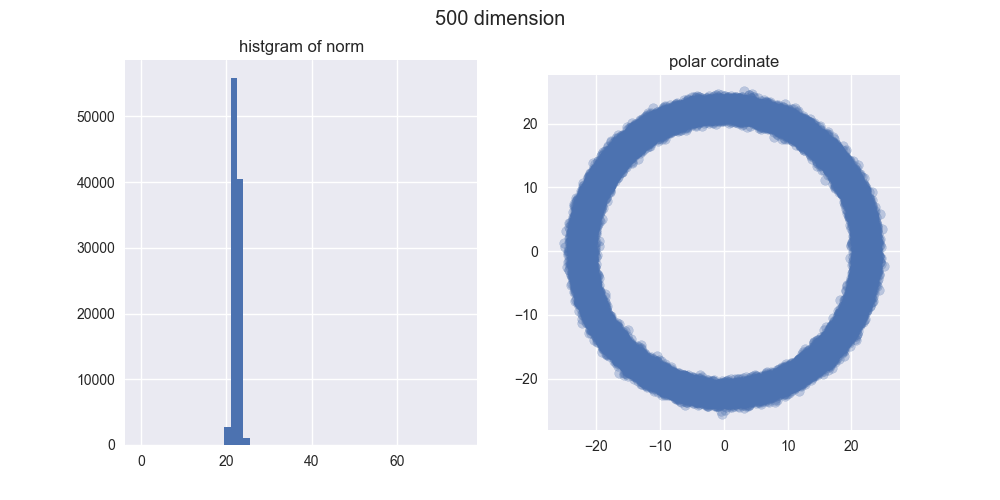
とは言え、5000次元ぐらいでも我々の直感とはかなり違う結果になったのではないでしょうか？左のヒストグラムからは、ノルムがどんどん大きくなることが分かりますし、右の図からは中心がポッカリ空いていくことが分かりますね。

え？「実際にはドーナツやん！」ですって？ご安心ください。異なる次元の図を見比べてみると分かるんですが、次元が大きくなるほどノルムが大きくなっていくので、ドーナツのスケールはどんどん大きくなっていくんですね。その割にはドーナツの「厚さ」はそれほど変わっていないので、相対的に厚さが限りなく薄くなり、ほとんど超球面になってしまうと考えられます。

アニメでまとめてみた

まとめ

いかがだったでしょうか？⁴次元が大きくなると我々の直感とはかけ離れた現象がおきてしまうことを、畏怖の念を込めて次元の呪いと呼びますが、あの正規分布ですら次元の呪いには勝てないということですね…皆さんもデータ解析の場面で高次元データを取り扱う際には注意してください！

追記（2021/02/08）

@s_katagiri さんからこの球面集中がどのような確率分布において起こるかの条件について述べている論文を教えていただきました。厳密な話を知りたい方はこちらを参照されると良いかもしれません。
https://doi.org/10.11429/sugaku.0653225
https://ci.nii.ac.jp/naid/110009649320

付録：高次元空間中だとほとんどのベクトルのペアはコサイン類似度が0に近くなる？

実験をしていた初期では、角度$\theta$を以下のコサイン類似度を用いて計算しようとしていました。
$$
\theta=\cos^{-1}\left(\frac{\mathbf{x}^\mathrm{T}\mathbf{e}}{||\mathbf{x}||||\mathbf{e}||}\right)
$$
ここで$\mathbf{e}$は角度$\theta$を求めるための基準となる単位ベクトル$\mathbf{e}=(1,0,\dots,0)^{\mathrm{T}}$です。では、求めた$\theta$を用いて作成したグラフが以下です！

ただし、$\cos^{-1}$の値域は$[0,\pi]$なので、ランダムに符号を反転させて見やすくなるようにしています。

…え？なにこれって感じですね。角度が$\frac{\pi}{2}$もしくは$-\frac{\pi}{2}$に集中してしまっています。これはなぜかというと関数$\cos^{-1}$の中身、つまりコサイン類似度がほとんど0になるからです。
これはコサイン類似度の定義を見るとすぐに分かります。今回の場合は基準となるベクトルを$\mathbf{e}=(1,0,\dots,0)^{\mathrm{T}}$としているため、$\mathbf{x}^\mathrm{T}\mathbf{e}$という標準内積は$\mathbf{x}$の第一成分を取り出す操作となっています。これは標準正規分布に従っていますから、一番最初に見た確率密度関数の通りのスケールです。にも関わらずどんどん大きくなる$||\mathbf{x}||$で除算していますから、コサイン類似度はほとんど0になってしまうわけです。

コサイン類似度というとてもベーシックなツールでも、高次元空間で用いる際にはこんな現象があるんだということをきちんと認識する必要がありますね。またしても高次元恐るべし…という一例でした。

1. "High-Dimensional Probability -An Introduction with Applications in Data Science-" のsection3.3.3にあるFigure3.6をそのまま掲載。英語ですがフリーで見れますしかなり丁寧に書いてあるのでオススメです。ちなみにこちらのツイートを見てこの画像を知り、衝撃を受けてこの記事を書くことにしました。ツイート主の方、重大な事実を教えていただきありがとうございました。 ↩ ↩²

2. こちらのページを参考にしました。こちらではよりgeneralに共分散行列を$\sigma^2\mathbf{I}_n$としています。
   $$
   E(||\mathbf{x}||)=\frac{\sqrt{2} \Gamma\left(\frac{n+1}{2}\right)}{\Gamma\left(\frac{n}{2}\right)}
   $$
   ガンマ関数$\Gamma$が出てきちゃって分かりにくいのですが、このような不等式で表すことができます。
   $$
   \frac{n}{\sqrt{n+1}} \leq E(||\mathbf{x}||) \leq \sqrt{n}
   $$
   つまり、次元$n$が大きくなるほどノルムの期待値は増大します。期待値が大きいと言うことは、大きいノルムを取る$\mathbf{x}$ばかりがサンプリングされ、ノルムが小さい（＝原点に近い）$\mathbf{x}$はほとんどサンプリングされないため、超球面状に分布するよということだったんですね³。ちなみに$n$が大きくなるほど$E(||x||)\simeq\sqrt{n}$になるので、超球面の半径は$\sqrt{n}$に近づくことがわかります。 ↩

3. 確率変数である$||\mathbf{x}||$の期待値だけ見て超球面状に分布することを断定していますが、本当は期待値だけではなく分散やそれ以上の高次モーメントを見て、$||\mathbf{x}||$の確率分布がシングルピークかつ分散が小さいことを示さなければならないはずです。今回はそこまで解析的に解くことはしていません。その代わりシミュレーションでヒストグラムを示しています。前述した文献¹では極座標表示を用いてそのあたりを厳密に示しているのでとてもオススメです。こちらのブログでもかなりスマートに説明されているので、オススメです。 ↩

4. 言ってみたかった ↩