知識グラフは特殊な関係データ？

自身の研究に関係ありそう、ということで知識グラフ（Knowledge Graph）について調べていたんですが、あれ？これって関係データと似てね？と思ったのでその辺りについての気づきのメモです。関係データについてすでに知っている方に向けて知識グラフについての結論を書くと以下のような感じです。

• 知識グラフはサブジェクト、オブジェクト、関係の3つのオブジェクトに組み合わせに対する三項関係データ
• 観測される値は「観測されたか・されてないか」の二値
• サブジェクトとオブジェクトは同一ドメインなので全体のドメインの数は2

知識グラフの定義

知識グラフはものすごくざっくり言うと、「エッジの種類がたくさんある有向グラフ」です。図で示すとこんな感じ

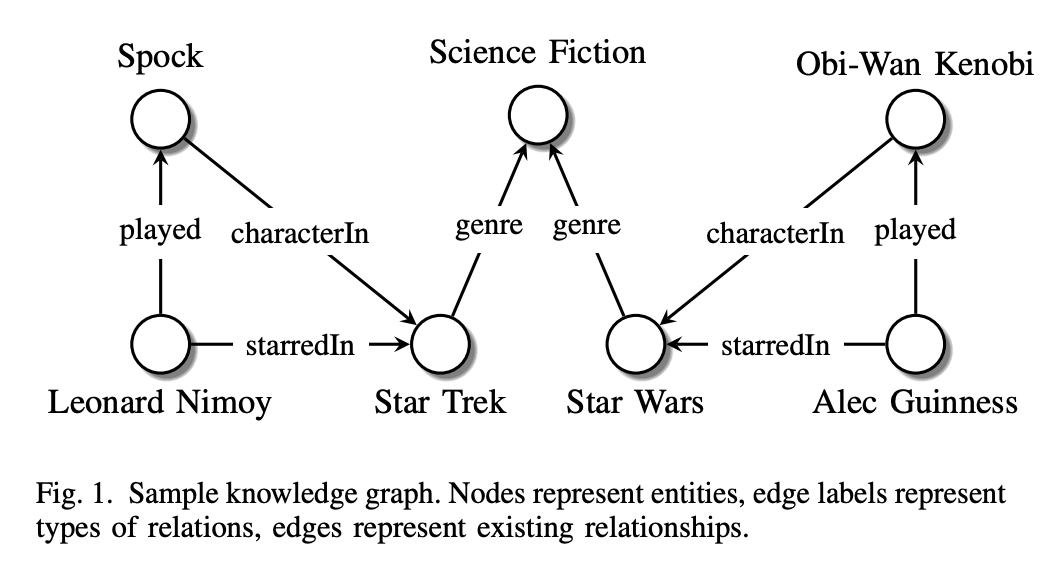
（[1]より引用）

実は厳密な定義はないらしいのですが、今回は[2]の定義を引用したいと思います。知識グラフではノードのことをエンティティ、エッジのことを関係と言います。例えば上の図の一部を切り取ると、「Star Trek」というエンティティから「genre」という関係が「Science Fiction」というエンティティまで伸びています。これによって『「Star Trek」は「Science Fiction」という「genre」である』という「知識」を表現できているわけですね。この3つ組のことを知識グラフでは事実と呼びます。また、矢印の元側のエンティティをサブジェクト、矢印の先側のエンティティをオブジェクトと呼びます ¹。

ちょっと真面目に数式で定義してみましょう。エンティティの集合を$V$、取りうる関係の集合を$R$と定義します。この時、1つの事実はサブジェクト$e_i\in V$、オブジェクト$e_j \in V$、関係$r_k \in R$の3つ組$(e_i,e_j,r_k)\in E$として表現できます。$E$は観測されている事実の集合で$E\subset V\times V \times R$です。この時、$G=(V,R,E)$を知識グラフと呼びます。

関係データの定義

皆大好きMLPシリーズの『関係データ学習』[3]にまとまっているので、さらっとご紹介します。

関係データとは『複数のデータの間に観測、定義される「関係」に着目したデータ』のことです。例えばtwitterのようなSNSであれば「ユーザ」と「ユーザ」の間に「相互フォロー」という関係が定義でき、「相互フォローしているかしていないか」という2値が観測されます。またAmazonなどのECサイトにおける5つ星評価のようなデータであれば、「顧客」と「商品」の間に「評価」という関係が定義され、「評価値」という$\{1,2,3,4,5\}$のどれかを取る値が観測されるわけです。関係データでは特定のユーザ、特定の商品、特定の顧客のことを一般化してオブジェクトと呼びます。

ここから関係データの用語を使って知識グラフを説明したいので、関係データの種類をかなりざっくりとまとめておきます。詳しくは[3]かもしくはそれをまとめているこの記事を参考にしてください。

• ドメインの数に着目した分類
  • 単一ドメイン関係データ
    • 同じ種類のオブジェクトの組み合わせに対して観測される関係データのこと
    • e.g. SNSのユーザとユーザの相互フォローという関係データ
  • 複数ドメイン関係データ
    • 異なる種類のオブジェクトの組み合わせに対して観測される関係データのことを
    • e.g. ECサイトの商品と顧客
• 組み合わせの数に着目した分類
  • 二項関係
    • 2つのオブジェクトが組み合わさって観測される関係データ
    • e.g. SNSのユーザとユーザ、ECサイトの商品と顧客
  • M項関係（Mは二以上の整数）
    • M個のオブジェクトが組み合わさって観測される関係データ
    • e.g. 脳波の測定データ。「電極位置」と「時刻」と「周波数」の組み合わせに対して「電圧値」という連続値が観測されており、三項関係データになる。
    • 二項関係データの一般化
• 関係の向きを考慮する必要があるか
  • 有向関係データ
    • 関係の「向き」を考慮する必要がある関係データを有向関係データと呼ぶ。
    • e.g. 「フォロー」という関係を定義されたSNSのユーザとユーザの関係データ。フォローしている・されているという「向き」が生じ、オブジェクト同士を入れ替えてしまうと関係が変わってしまうため有向。
    • 二項かつ有向な関係データで有向グラフとして表現される
  • 無向関係データ
    • 関係性の「向き」を考慮する必要がないもの。
      • e.g. 「相互フォロー」という関係が定義されたSNSのユーザとユーザの関係データ。オブジェクト間を入れ替えても同じ関係を表現しているため、無向。

二項関係データの場合はグラフとして表現されることが多いです（有向、無向というのはグラフから来た呼び方）。一方で三項以上になってくるとテンソル（多次元配列）として表現されることが多いです²。

知識グラフは特殊な関係データ

知識グラフの定義を思い出すと、知識グラフとは$G=(V,R,E)$であり、$V$はエンティティの集合、$R$は関係の集合、$E$は観測されている事実の集合でした。$E$の要素は$(e_i,e_j,r_k)$と表現されます。つまり知識グラフはサブジェクト$e_i$、オブジェクト$e_j$、関係$r_k$の間に「観測されたかされていないか」という2値が与えられる三項関係データと言えます。また、サブジェクトとオブジェクトは$V$という共通したドメインですが、関係は異なるドメインであるので、三項関係ではあるがドメインは2つということになります。

ということで知識グラフは特殊な関係データと見なすことができるため、関係データの解析手法をそのまま使うことができます。観測されていない事実を推定するタスクをKnowledge base completionと言いますが、[3]によるとこれには関係データの欠損値推定に使われるテンソル分解が適用されるようです³。

終わりに

ということで関係データとしての知識グラフについて最後にまとめると以下のようになります。

• サブジェクト、オブジェクト、関係の3つのオブジェクトに組み合わせに対する三項関係データ
• 観測される値は「観測されたかされてないか」の二値
• ドメインの数は2

関係データを扱っている皆さんはぜひ知識グラフも扱ってみましょう！！！

余談：『関係データ学習』にある関係データの定義をしている英語文献があったら、どなたか教えてください。

参考文献

[1] Maximilian Nickel, Kevin Murphy, Volker Tresp, Evgeniy Gabrilovich. "A Review of Relational Machine Learning for Knowledge Graphs." https://arxiv.org/abs/1503.00759
[2] 林 克彦, 上垣外 英剛. "知識グラフデータベースの表現学習"
[3] 石黒 勝彦, 林 浩平. "関係データ学習"

---

1. 国語の授業っぽく解釈すると「Star Trek」は主語、「genre」は述語、「Science Fiction」は目的語に相当するものですね。この3つ組を知識と呼んでいるのが個人的には面白ポイントです。要素と要素の関係性を理解することが「知識」なんだっていう。 ↩

2. 二項関係データの場合でもテンソルで表現することもあります。その場合は行列になります。一方でグラフの方でも三項以上の関係を表現するために任意個のノードを連結できるハイパーグラフというのがあるそうなので、二項だからグラフ！三項以上だからテンソル！とも言えないようです。 ↩

3. 知識グラフのデータの収集のされ方を考えると$e_i$と$e_j$の間に$r_k$という関係が「存在している」ということは観測できますが、「存在しない」ということを観測することは難しそうですね。Knowledge base completionを行う際に[2]では３階のテンソルを用意して、観測されていれば1、観測されていなければ0としているようですが、厳密なことを考えだすとこの辺りの扱いは結構面倒な気がします。 ↩