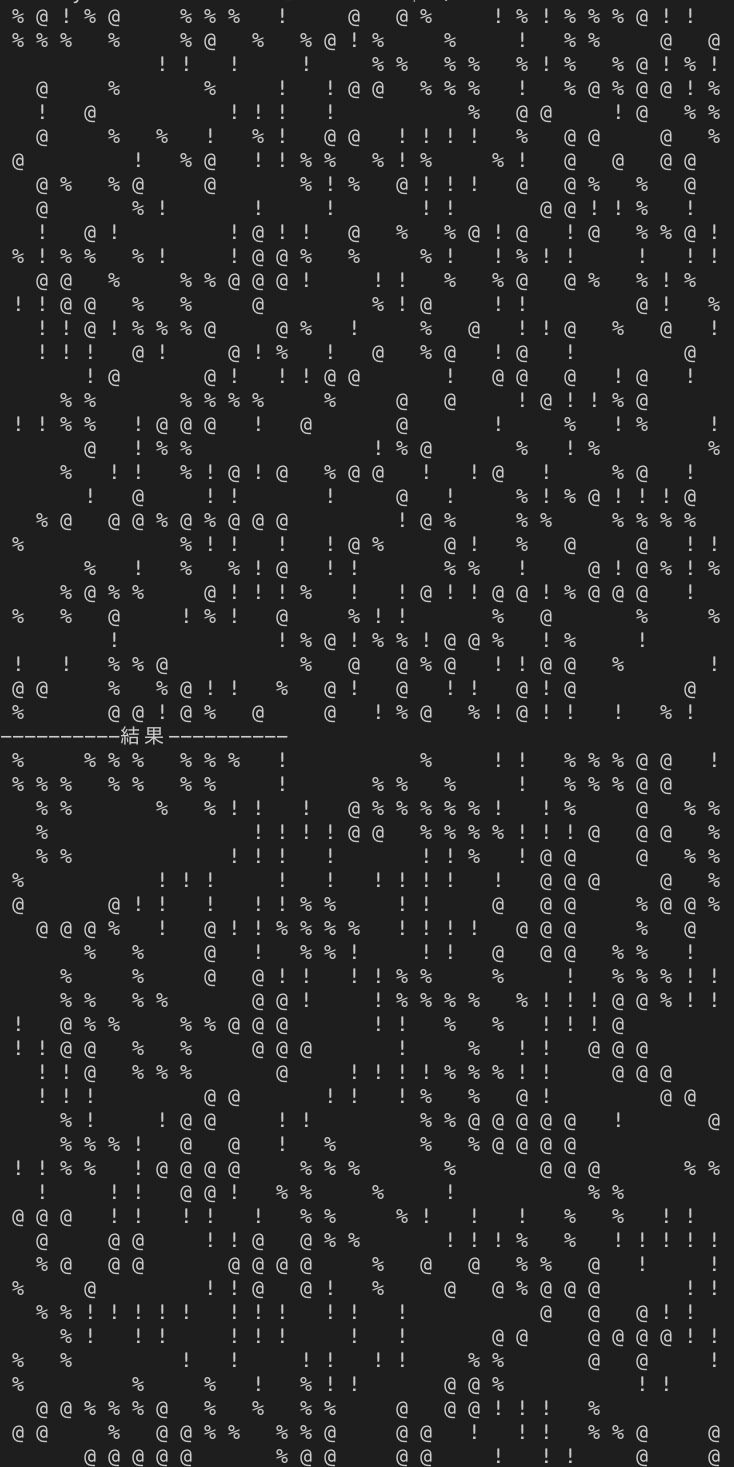0　はじめに

「シェリングの分居モデル」というものを、C++という言語を用いて実装します。C++を使ったことがない人にも分かるよう、なるべく単純な実装を心がけましたが、そんなに分かりやすくないかもしれません。
おかしいところ、分かりにくいところ等ありましたら、コメントとかで教えてくださると嬉しいです。

0-1 分居モデルとは

トマス・シェリングというアメリカの経済学者（2005年ノーベル経済学賞を受賞）が、1969年に発表したものです。
地域社会が人種ごとに分居する傾向にあることに注目し、ミクロレベル（人々の個人的な好みや行動様式）から推測できることが、必ずしもマクロレベル(社会全体の有様)に反映するとは限らないことを定式化した、マルチエージェント・シミュレーションを社会学に取り入れた原点ともいえるものです。

0-2 今回実装するモデルの仕組み

分かりやすくゲームっぽく説明します。

このシミュレータには、碁盤のように整理された居住区が存在します。
3種類の人種が存在していて、それぞれを「％人種」、「＠人種」、「！人種」と呼称します。
人々は、この碁盤の線が交わる点（整数値の座標で管理ができるため）に住むことができます。
このシミュレータ上で生活する人々は、各ターンに自分の周り（縦、横と斜めの合計8マス、これを近隣住民とします）を見渡し、同人種が近隣住民のうち1/3以上存在した場合に安心し、そこに住み続けます。
安心できない場合は、居住区のランダムな場所に引っ越します。
居住区に存在する全住民が安心した場合にシミュレーションを終了します。

近隣住民のうち3分の１だけ同人種が存在すれば良いわけですから、かなり異人種に寛容的に思えますよね？
結果をシミュレーションで確かめてみましょう。

1 実装

順番に実装していきましょう。
＃1-1~4を全て上からコピーして順番に配置するだけで実行できます。

1-1 準備

人口とか住所を保管する配列とか定義していきましょう。
最初の7行はおまじないなのでC++わからない人は無視してください。

#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#include<iostream>
#include<utility>
#include <iomanip>
using namespace std;


#define BOARD_WIDTH 30
#define BOARD_HEIGHT (BOARD_WIDTH)
#define population 500
int board[BOARD_HEIGHT][BOARD_WIDTH];
pair<int,int> address[population];

int dx[8]={-1,0,1,-1,1,-1,0,1};
int dy[8]={1,1,1,0,0,-1,-1,-1};

char symbol[4]={' ','%','@','!'};//表示用のシンボル

BOARD_WIDTHとBOARD_HEIGHTはボードの大きさです。boardという配列に人種を登録します。
populationは人口です。この3つの値は自由にいじっていいですが、必ず（BOARD_WIDTH)×(BOARD_HEIGHT)>populationとなるように気をつけてください。１マスも空き地がないと引っ越しが出来なくなってしまいます。
addressは戸籍みたいなものです。人に住所（座標）を紐付けるために使います。pairという型で直交座標x,yを格納しています。
dx,dyは見渡す時に使うものです。これを定義しておくとfor文で回すだけで周りを確認できるので後で楽になります。
symbolは人種の表示用に使います。

1-2 初期配置

board上に人々を住まわせていきましょう。完全にランダムに決めていきます。

void prepare(){
    for (int i=0;i<BOARD_HEIGHT;i++){ //全住所を-1で初期化
        for (int j=0;j<BOARD_WIDTH;j++){
            board[i][j]=-1;
        }
    }

    for (int i=0;i<population;i++){
        int x=rand()%BOARD_HEIGHT;
        int y=rand()%BOARD_WIDTH;
        while(board[x][y]!=-1){//空き地でなかった場合繰り返す
            x=rand()%BOARD_HEIGHT;
            y=rand()%BOARD_WIDTH;
        }
        board[x][y]=rand()%3;//人種の決定
        address[i]=make_pair(x,y);
    }
}

void とは戻り値のない関数のことです。
全住所を-1で初期化してから人口分の住所を生成しています。この時に住所がダブらないように気をつけてください。

1-3 描画用の関数

void draw(){
    for (int x=0;x<BOARD_HEIGHT;x++) {
        for (int y=0;y<BOARD_WIDTH;y++)
            cout << setw(2) << symbol[board[x][y]+1];
        cout << endl;
    }
}

シミュレーション上の空間を描画します。setw(2)は、2文字分のマスに表示をしてね、という意味で、見やすくするためだけの工夫です。

1-4 メイン関数

int main(){
    srand((unsigned int)time(NULL));//乱数を時間で初期化
    prepare();
    draw();

    bool flag=false;
    while(!flag){
        flag=true;
        for (int i=0;i<population;i++){
            int x=address[i].first,y=address[i].second;
            int countSame=0,countDiffrent=0;
            for (int j=0;j<8;j++){
                if (x+dx[j]<0 or x+dx[j]>=BOARD_HEIGHT or y+dy[j]<0 or y+dy[j]>=BOARD_WIDTH){//範囲外
                    continue;
                }
                if (board[x+dx[j]][y+dy[j]]==-1){
                    continue;
                }else if(board[x+dx[j]][y+dy[j]]==board[x][y]){
                    countSame++;
                }else{
                    countDiffrent++;
                }
            }   
            if (countSame*2<countDiffrent){//安心できない場合
                flag=false;
                int race=board[x][y];
                board[x][y]=-1;
                x=rand()%BOARD_HEIGHT;
                y=rand()%BOARD_WIDTH;
                while(board[x][y]!=-1){//空き地でなかった場合繰り返す
                    x=rand()%BOARD_HEIGHT;
                    y=rand()%BOARD_WIDTH;
                }
                address[i]=make_pair(x,y);
                board[x][y]=race;
            }

        }
    }
    cout << "----------結果----------" << endl;
    draw();
}

ルール通りの実装です。一番最初のsrand((unsigned int)time(NULL))は、乱数の初期化です。
flagというブール値が最後までtrueを保ち続けたら、全住民が安心して暮らしているということなので、ループを終了します。

2 実行結果

どのような結果になりましたか？最終的にかなり分居が進んでいるのが確認できたと思います。
自分が手元で実行した結果はこんな感じです。

下半分が結果です。陣取り合戦みたいになってますね......
適当なタイミングでdraw関数を入れて、分居の進み具合を確認してみるのも面白いです。

3 終わりに

いろいろなパラメータをいじって遊んでみてください。人種によってルールを変えてみたら、より面白いデータが得られるかもしれません。
この間アメリカからの帰国生の友達にこのモデルを見せたら「3分の1も同人種が必要なのはなかなかのレイシストだ」みたいなことを言われました。すごいですね.....自分はずっと日本に住んでいるので、こんな環境には耐えられないかもしれません。（決してレイシストとかではないです。慣れていないので落ち着かないだけ）

4 参考文献

人工社会構築指南―artisocによるマルチエージェント・シミュレーション入門(山影進　著)を参考、一部引用させていただきました。ありがとうございます。

C++でシェリングの分居モデルを実装する

0 はじめに