1.はじめに
先日ようやく統計検定準1級から解放されました。
1回目の受験で不合格で、2回目の受験で合格。
合格したと言っても結果は以下の通り散々でした
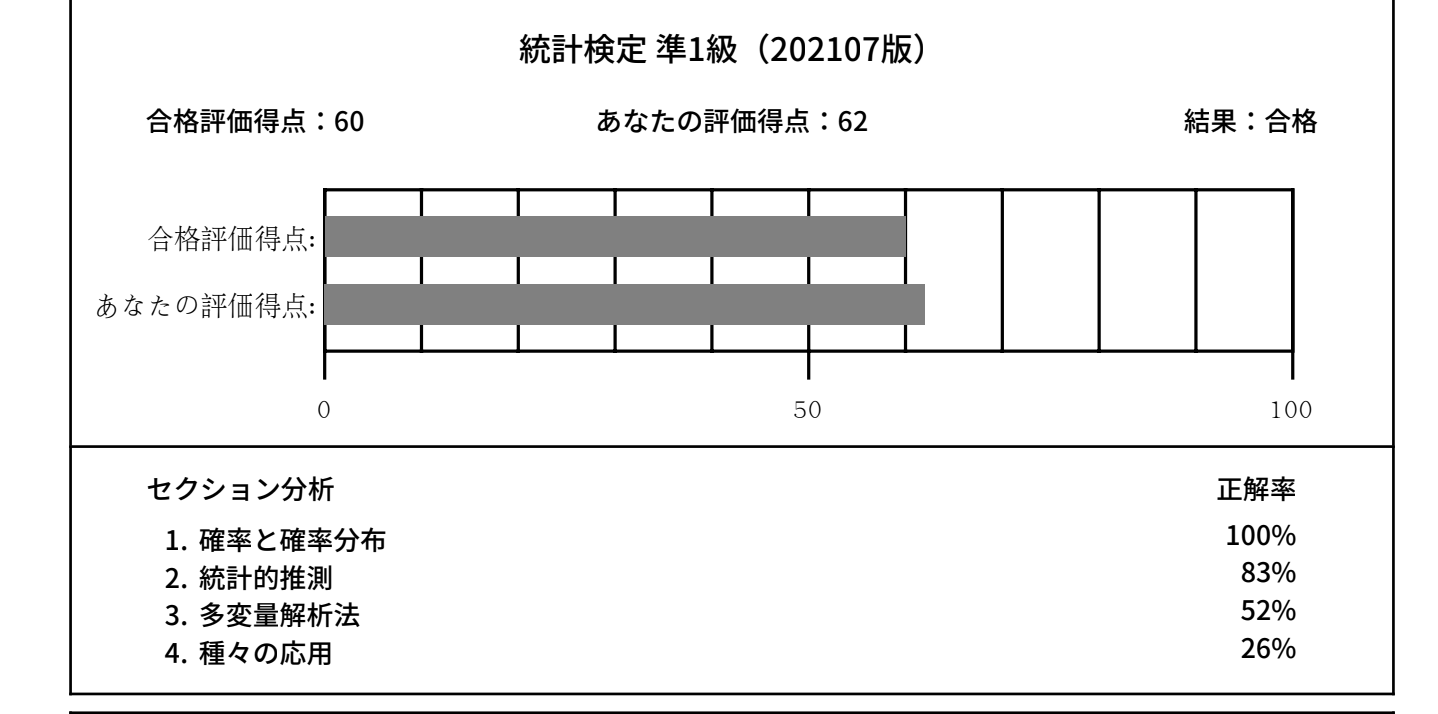
確率分布と統計的推測は良かったのですが多変量解析と応用はボロボロです。
偉そうにアドバイスができる立場ではありませんが、合格するために学習したことについてまとめます。
2.受験前のスキルレベル
- 大学では統計学(統計検定2級レベル)と線形代数の単位をぎりぎり取得できる程度の数学力しかなく、それ以降は数学に触れずに過ごす
- 2年ほど前に統計検定2級に合格
3.ざっくりとした学習方針
1回目の受験
- 2級と比べて試験範囲が驚くほど広いので、ワークブックと過去問で満遍なく勉強する(結果的にこれがダメでした)
- 試験範囲を見る限り高度な計算力は求められないと思ったので、ワークブックに記載されている数式だけは理解することを徹底した(この方針も僕には合わなかったかもです)
2回目の受験
- 実際の問題をみてみると、ワークブックだと軽く1行で説明している部分も平気で出題されることがわかった。そのため隅から隅までワークブックを読み、わからない部分は他の参考書で補強するという方針に変更。
- 数学力に関しては深く求められないということがわかったが、後々統計検定1級も受けるつもりだったので、わからない数式は徹底的に調べて写経して理解するという方針に変更。
4.学習に使用した教材
4.1.必須級
-
統計検定 準1級 公式問題集
当然ですが必須です。試験ではかなり細かい部分も出題されるので、ワークブックは1行1行理解する必要がありそうです。
過去問は実際に出題される問題と傾向が異なる印象ですが、自分の理解度を把握するためにもやっておくべきだと思います。 -
統計学のための数学入門30講
準1級範囲外の部分が多いですが統計学に使われている数学が網羅されているため、個人的には数学的な理解を重視する場合は必須でした。 -
現代数理統計学の基礎
こちらも準1級範囲外の部分が多いですが、ワークブックに記載されている内容をより深く理解したい場合に重宝しました。恐らくこの本のおかげで確率分布と統計的推測の点数がよかったのだと思います。 -
統計検定 2級 公式問題集
準1級の範囲と被っている部分、特に仮説検定・区間推定の計算は完璧にしておくといいかもしれません。 -
多変量解析法入門
小規模データを使って、重回帰分析・判別分析・主成分分析・クラスター分析などを手計算でやってみるという書籍。
これがなかったら多変量解析は0点だったかもしれないです。
ただし、この本で解説されていないが試験範囲に該当する手法がいくつかあるので、そこは別途学習する必要がありそうです。(良い本があれば教えていただけると幸いです) -
あつまれ統計の森(webサイト)
過去問・ワークブックの解説は細かい数式の展開が省略されていますが、こちらのサイトでは丁寧に途中式を書いてくださっているので滅茶苦茶参考にしていました。数式が理解できない場合はとりあえずこのサイトを見に行くことをお勧めします。
4.2.あったほうがいい
-
Rで学ぶ確率統計学 多変量統計編
3冊ともRで解説されている書籍ですが、読むだけでも理解できるように書かれている印象です。かなり幅広い範囲をカバーできるので読んで損をすることはないと思いますが、当然試験はRではなく電卓で計算する必要があるので、あくまで副教材的に使うのが良さそうです。
5.合格後に感じたこと
結局のところワークブックのみで合格するのは不可能な気がします。
一方、他の書籍だと準1級範囲外の部分も扱っている場合が多いです。
そのため合格だけを目指した効率の良い勉強はしづらい印象です。
いっそのこと、1級に合格できるレベルの理解度を目指した方が長期的にみて効率がいいかなと思います。。。
役に立ちそうな書籍があれば随時追加したいと思います。
少しでもお役に立てれば幸いです。