More than 1 year has passed since last update.

機械学習で歌舞伎町ライブカメラの人流を3D化してみる

Last updated at 2023-02-08Posted at 2023-02-05

はじめに

この記事は「画像処理系の技術をつかってなにか作ろう！」というゆるい授業で作成したグループ自由課題を抜粋・一部改変して投稿したものです。
モデルの考案やシステムの開発は自分で行いましたが、Introductionでの調査や、実地測定はグループメンバーに手伝ってもらっています

学術論文っぽい体裁になってますが中身はエンジョイ企画なので軽い気持ちで読んでいってください！

先に結果をみたい方はこちら！！

🥚 Abstract

本プロジェクトでは莫大なサイズにもなりうるデータを利用価値を落とさずに、すなわち特定の人物の追跡などが可能な質を保ったまま効率的に保管・処理する手法を提案する。

新宿歌舞伎町に設置されている2台の防犯カメラに映る通行人を検出し、防犯カメラの仰俯角・方位角を推定した上でそれらの座標を3次元座標に変換した。複数の防犯カメラ映像から得られる座標群を合成することで2カメラに映る人物の同一判定を自動で行い、人流の追跡に十分な精度の3Dマッピングに成功した。

また、チェス盤模様のボードを用いる従来のカメラキャリブレーションでは、仰俯角・方位角の推定をする上での一般的な防犯カメラの特性上の課題があることを発見し、いくつかの近似を行った上で勾配降下法でパラメータを推定するオリジナルの手法を用いた。

🐣 Introduction

近年防犯カメラはアナログカメラではなくネット経由で映像を確認・管理できる、より高画質なネットワークカメラが主流になってきている。しかし、通信量・データ量の増加により、保管や分析が課題となっている。

解像度が3840×2160 の超高画質(4K)の場合、必要な通信速度は約25Mbpsで1時間あたりの通信量は約11.25GB。
HDDやクラウドに保存する際のデータ量は、録画時間1か月で2TB。

一定期間を過ぎると自動的にデータが上書きされるものもあり、防犯カメラの映像そのものを保管して分析することが難しくなっていくと予想される。カメラの人流の動きに限定して別の形態のデータで保管して活用することを目指せるのではないかと考えた。

利活用例

工場・職場・スーパー等での人流解析
複数カメラを使って、特定の人の動きを真上から見た経路に変換することができれば、移動の円滑化や、施設の配置の最適化の分析に役立つのではないか。
人の追跡
迷子センターにおける迷子の居場所の特定や、犯人の逃走経路の特定などをする際に監視カメラの映像を目で確認して経路を確認するのは手間である。真上から見た対象物の移動経路を座標として可視化することができれば犯人の追跡も容易になるのではないか。

🐤 Methodology

0. 前提知識

カメラのもつパラメータ

外部パラメータ
カメラの3次元並進ベクトル、回転行列
内部パラメータ
焦点距離、光学中心、せん断係数
歪みパラメータ
レンズの半径方向歪み、円周方向歪み

座標系

ワールド座標系
基準となる三次元座標系。
本プロジェクトでは右手系、鉛直方向上向きをz軸とし、長さの単位はメートルとする。
カメラ座標系
カメラ視点を原点とする三次元座標系。外部パラメータによってワールド座標系と相互に変換できる。
本ドキュメントではカメラの向く方向にz軸、カメラから見て水平方向右向きにx軸、鉛直方向上向きにy軸をとる。
スクリーン座標系
カメラのスクリーン上の点を映すための二次元座標系。
本ドキュメントでは原点中央、右向きにx軸、上向きにy軸をとる。

本ドキュメントでの変数名

スクリーンのアスペクト比 $R$
スクリーンの横の長さを縦の長さで割ったもの。ex. 16:9なら$R = 16/9$
スクリーン座標系での座標 $(x_{screen}, y_{screen})$
スクリーン座標系で画面に写っている領域 $D_{screen}$

$[-0.5, 0.5]\times [-0.5/R, 0.5/R]$の直積で表される
カメラ座標系のz軸方向単位ベクトルをワールド座標系に写したもの $\boldsymbol{n_{world}}$
カメラ座標系のx軸方向単位ベクトルをワールド座標系に写したもの $\boldsymbol{a_{world}}$
カメラ座標系のy軸方向単位ベクトルをワールド座標系に写したもの $\boldsymbol{b_{world}}$

特に個別のカメラについて議論する場合は、各変数の右肩に1, 2の添字を加えそれぞれカメラ1, カメラ2についての量とする。

1. 通行人のスクリーン座標の取得

Googleの提供するクラウドサービス群GCP(Google Cloud Platform)のサービスの一つ、Video Intelligence APIを用いて動画中に映る人物の検出を行った。

Fig. 1-1 カメラ1で撮影された動画のアノテーション

Fig. 1-2 カメラ2で撮影された動画のアノテーション

これらのアノテーションのうち、画面上にプロットできている時間が長いバウンディングボックスの上辺の中点を人物の代表点として抽出した。バウンディングボックスとは認識されたエンティティ(この場合人物)を最小サイズで囲う境界線のことで、動画中の青枠のことである。すなわち代表点とはおおよそ人間の頭頂部にあたる。

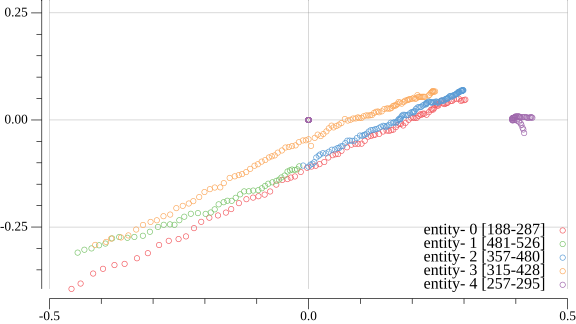
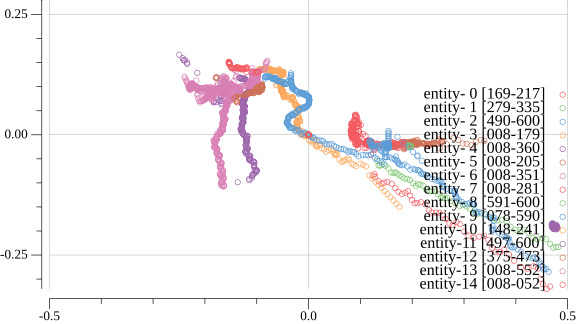
代表点のプロットを各時刻で重ねたものが下図。エンティティごとに色分けされている。凡例右のカッコ内の数字はエンティティが映像中に検出された時刻で単位は0.1秒。

Fig. 1-3 カメラ1の映像における代表点のプロット

Fig. 1-4 カメラ2の映像における代表点のプロット

2. カメラの傾き推定

カメラキャリブレーション

広く用いられている手法としてカメラキャリブレーションがある
キャリブレーションボードという通常チェスボード模様の平板を複数回カメラの画面に映すことで各種パラメータを推定するという方法で、実際に以下のようなお手製キャリブレーションボードを用いて推定を試みた。

Fig. 2-1 クイックルワイパーを用いたキャリブレーションボードの製作

Fig. 2-2 柄の部分を分解してカメラ設置場所に持ち運ぶ

Fig. 2-3 防犯カメラに映るキャリブレーションボード

チェス盤を正確に認識することができなかった

Fig. 2-4 自宅で撮影したキャリブレーションボード

チェス盤の各点の座標が正確にプロットされている

OpenCVの実装で自宅で撮影した画像からは正しくチェスボードの格子点の座標が取得できたものの、防犯カメラに映るボードは正確に検出することができなかった

その原因としては以下が挙げられる

防犯カメラの画質がボードの認識に十分でなかった
今回用いたスマホカメラの画素数は4608 × 3456、防犯カメラの画素数は1920 x 1080で総画素数は7.68倍もの差があった
防犯カメラの位置が高く、ボードを大きく映すのが困難だった
広い範囲の地面をカメラの枠内に収めるために防犯カメラは高い位置に設置されやすい。実際今回研究対象としたカメラはどちらも地上から4mほどの高さにあり(後述)、クイックルワイパーを用いても撮影が困難だった。

一般に防犯カメラの画素数は2019年時点で100万~400万画素といわれ、こうした問題は多くの防犯カメラについてあてはまるといえる

See also: 防犯カメラの画素数を選ぶには？

より大きなボードを用意するという対策も考えられるが、防犯カメラシステムの構築に巨大ボードを用意する手間や、２つのカメラに同時にボードが完全に映らなければならないなどの制約から現実的ではないと判断し、次に述べる手法を用いることとなった。

オリジナルの手法

まず、いくつかの近似を行う

2カメラは歪みのない理想的なピンホールカメラである。すなわち歪みパラメータを考慮しない。
推定に用いる歩行者の頭頂は地面から1.7 mの高さである。以降ワールド座標系で $z = 1.7$ の平面を$\alpha$平面と呼ぶ。
2カメラの光軸方向の傾きは無視できる

さらに、既知の情報として

2カメラのワールド座標 $\boldsymbol{c_{world}}$
2カメラの垂直画角 $\psi_{vertical}$
2カメラのスクリーンのアスペクト比 $R$

を持つものとする。

その上で、各スクリーン上の同一人物の代表点を$\alpha$平面上に投影したものが一致するという事実を元にカメラの傾きを推定する。

今回はFig. 1-3のentity-0とFig. 1-4のentity-0が同一人物であることを用いた。

カメラ視点からスクリーン上の代表点に向けた半直線の方向ベクトル$\boldsymbol{d_{world}}$は

$$
\boldsymbol{d_{world}} = \boldsymbol{n_{world}} + k(x_{screen}\boldsymbol{a_{world}}+y_{screen}\boldsymbol{b_{world}})
$$

ここで$k$はスクリーン座標での点の移動が$\boldsymbol{d_{world}}$の傾きにどれだけ寄与するかのスカラー量で、$\psi_{vertical}$から求めることができる。

$$
\tan \psi_{vertical} = \frac{ \frac{k}{2R} \lVert \boldsymbol{b_{world}} \rVert}{\lVert \boldsymbol{n_{world}} \rVert} \ = \frac{k}{2R}
$$

$$
\therefore k = 2R\tan \psi_{vertical}
$$

推定するパラメータは

カメラ1, 2の仰角 $\theta$

下向きなら負の値をとる。
カメラ1, 2の方位角 $\phi$

ワールド座標系でx軸方向を0として反時計回りに正。

さらに、$\alpha$平面での通行人の軌跡の始点から終点へのベクトルの傾きが2カメラで一致するという制約から、全体として求めるパラメータの自由度は3とした。

これらを勾配降下法を用いて推定する。その際の設定変数は

ステップ数 $N = 100000$
(初期)学習率 $\mu_0 = 0.01$
数値微分の際の微小量 $dp = 0.01$

とした。ただし学習率$\mu$はステップ数$i , (0 \leqq i < N)$に応じて減衰させた。

$$
\mu = \mu_0exp(\frac{-4i}{N})
$$

また、損失関数は$\alpha$平面上の2点(同時刻の2カメラからの投影)の差ベクトルのL2ノルムを時間について足し合わせたものとした。

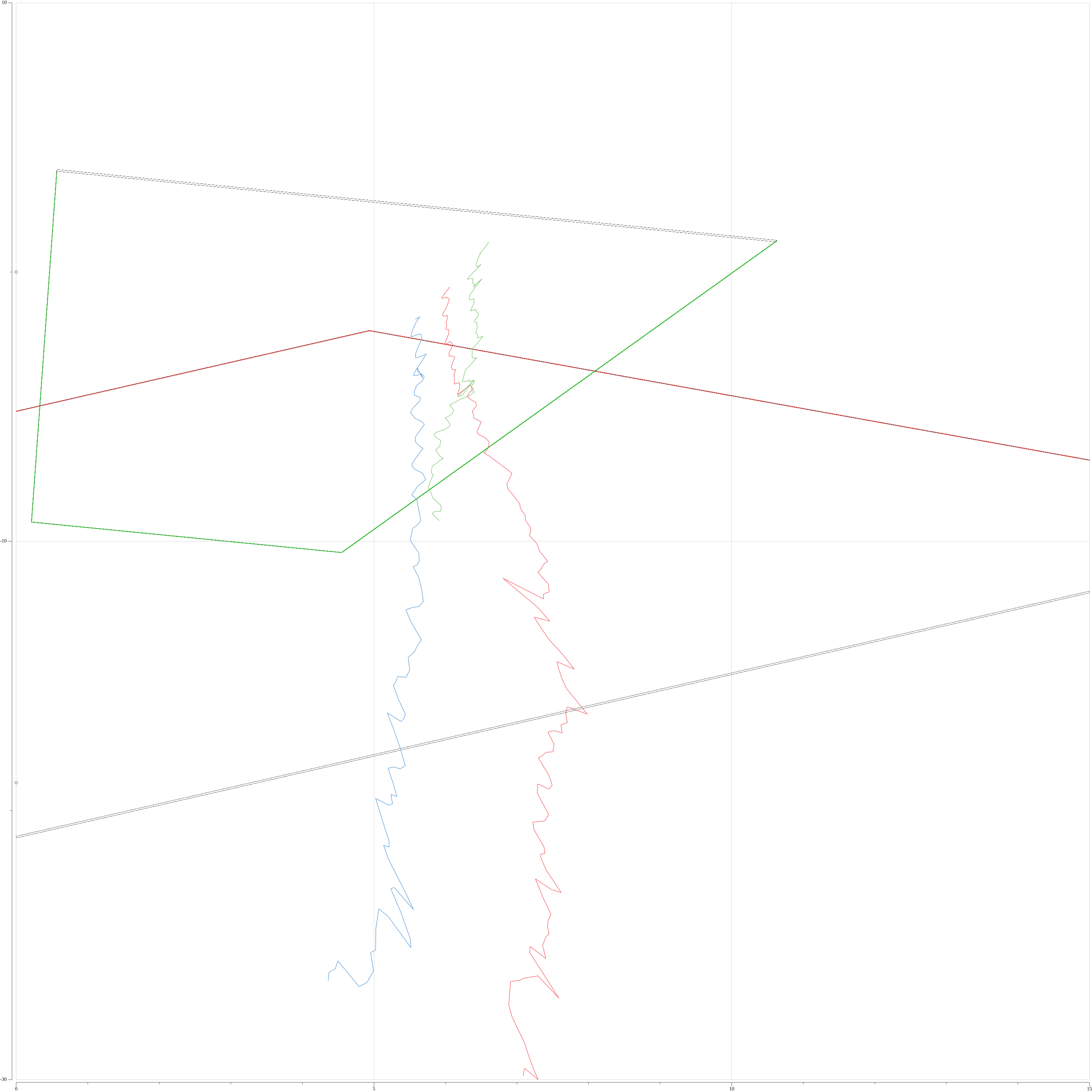
初期設定($\theta_1 = \theta_2 = -\frac{\pi}{2}, ,\phi_1 = \phi_2 = -\frac{\pi}{2}$)と学習後でのα平面上のプロットを下図に示す。カメラ1, 2からの代表点の軌跡をそれぞれ赤色、緑色のプロットで、カメラ1, 2のスクリーン下半分の投影をそれぞれ台形の赤枠、緑枠で表している。

仰角、方位角推定前のプロット

仰角、方位角推定後のプロット

赤色、緑色の代表点の軌跡がおおよそ重なっている。

推定によって得られたパラメータを下表に記す。

	theta (rad)	phi (rad)
カメラ1	-0.129	-1.025
カメラ2	-0.099	-1.315

3. 防犯カメラの各種パラメータの実測

研究対象の防犯カメラ2台が設置されている新宿歌舞伎町一番街に赴き、コンベックスメジャーを用いて実測を行った。

カメラ1の外観

カメラ2の外観

コンベックスメジャーを用いた実測の様子

カメラ1, 2のワールド座標

	地上からの高さ (m)
カメラ1	4.028
カメラ2	3.904

実測値は上表の通りで、2カメラの水平距離は18.97mであった。

得られたカメラ1, 2のワールド座標を下表に記す

	x	y	z
カメラ1	0	0	4.028
カメラ2	0	-18.97	3.904

カメラ1, 2の垂直画角

映像に映る適当な対象物に対して、実際の長さとスクリーン上の長さを比較することで垂直画角を算出した。対象物には長さを測りやすい直方体状のものを選んだ。

カメラ1での測定対象

カメラ2での測定対象

測定対象のワールド座標系での長さ $h_{world}$
測定対象のスクリーン座標系での長さ $h_{screen}$
カメラと測定対象との距離 $l_{world}$
垂直画角 $\psi_{vertical}$

	h_world	h_screen	l_world
カメラ1	1.80	0.0904	15.02
カメラ2	0.45	0.1623	5.931

スクリーン座標系での$D$の$y$座標の絶対値の最大値が$\frac{1}{2R}$であるから

$$
\tan{\frac{\psi_{vertical}}{2}} = \frac{\frac{1}{2R}\times\frac{h_{world}}{h_{screen}}}{l_{world}}
$$

すなわち

$$
\psi_{vertical} = 2\arctan{\frac{\frac{1}{2R}\times\frac{h_{world}}{h_{screen}}}{l_{world}}}
$$

で垂直画角が求められる

	psi_vertical (rad)
カメラ1	0.711
カメラ2	0.261

4. 同一人物判定

実測値を元に勾配降下法を用いて推定したカメラの傾きを用いて、各代表点群を$\alpha$平面上に投影することができる。

ここで、

カメラ$c$で検出されたエンティティの数 $n^c$

としてカメラ$c \in \{ 1, 2 \} $から$\alpha$平面上に代表点を投影されたエンティティ$i , (0 \leqq i < n^c)$について

投影後の軌跡(ワールド座標群) $track_i^c$
$track_i^c$の始点と終点が検出された時刻 $start_i^c, end_i^c$
時刻$t$での$track_i^c$のワールド座標 $(x_{screen, i}^{c}(t), y_{screen, i}^{c}(t), 1.7)$

ただし、$start_i^c \leqq t \leqq end_i^c$

としたとき、$track_i^1, track_j^2$の類似度を以下で定義する。

$$
sim(track_i^1, track_j^2) = - \frac{1}{end-start+1}\sum_{t=start}^{end} \rVert \begin{pmatrix} x_{screen, i}^1(t) \ y_{screen, i}^1(t) \end{pmatrix} - \begin{pmatrix} x_{screen, j}^2(t) \ y_{screen, j}^2(t) \end{pmatrix} \lVert
$$

ただし、

start = max \{ start_i^1, start_j^2 \} \\ end = min\{end_i^1, end_j^2\}

とし、$start > end$ となる組み合わせは考えない。

類似度を用いた同一人物判定アルゴリズムは以下の通り。

$k=0, A = \{0, 1, 2, ... , n^1-1\}, B = \{0, 1, 2, ... , n^2-1\}$とする
$track_i^1, track_j^2$の類似度が最も高くなるような組み合わせ$(i_k, j_k) \in A \times B$ を選ぶ
$sim(track_{i_k}^1, track_{j_k}^2)$ が閾値以上であれば同一人物であると判定、そうでなければ終了
$A, B$からそれぞれ$i_k, j_k$ を除外し、$k$ を一つ増やす
$A \neq \emptyset \land B \neq \emptyset$ であれば2に戻る、そうでなければ終了

3つ目のステップの閾値は1.0 m に設定した。

4つ目のステップは、アノテーションが正しく行われていればカメラ1で異なるエンティティがカメラ2では同じエンティティということはない(その逆もしかり)という前提に基づいている。

同一判定された2軌跡は時間が被っている点については元の2座標の中点をとって1つの軌跡に合成される。合成された軌跡をFig. 4-2に示す。

Fig. 4-1 各エンティティの代表点群をα平面上にプロットしたもの

カメラ1, 2どちらの画角にも入っている領域では同一人物の軌跡が赤と緑でおおよそ重なっている。

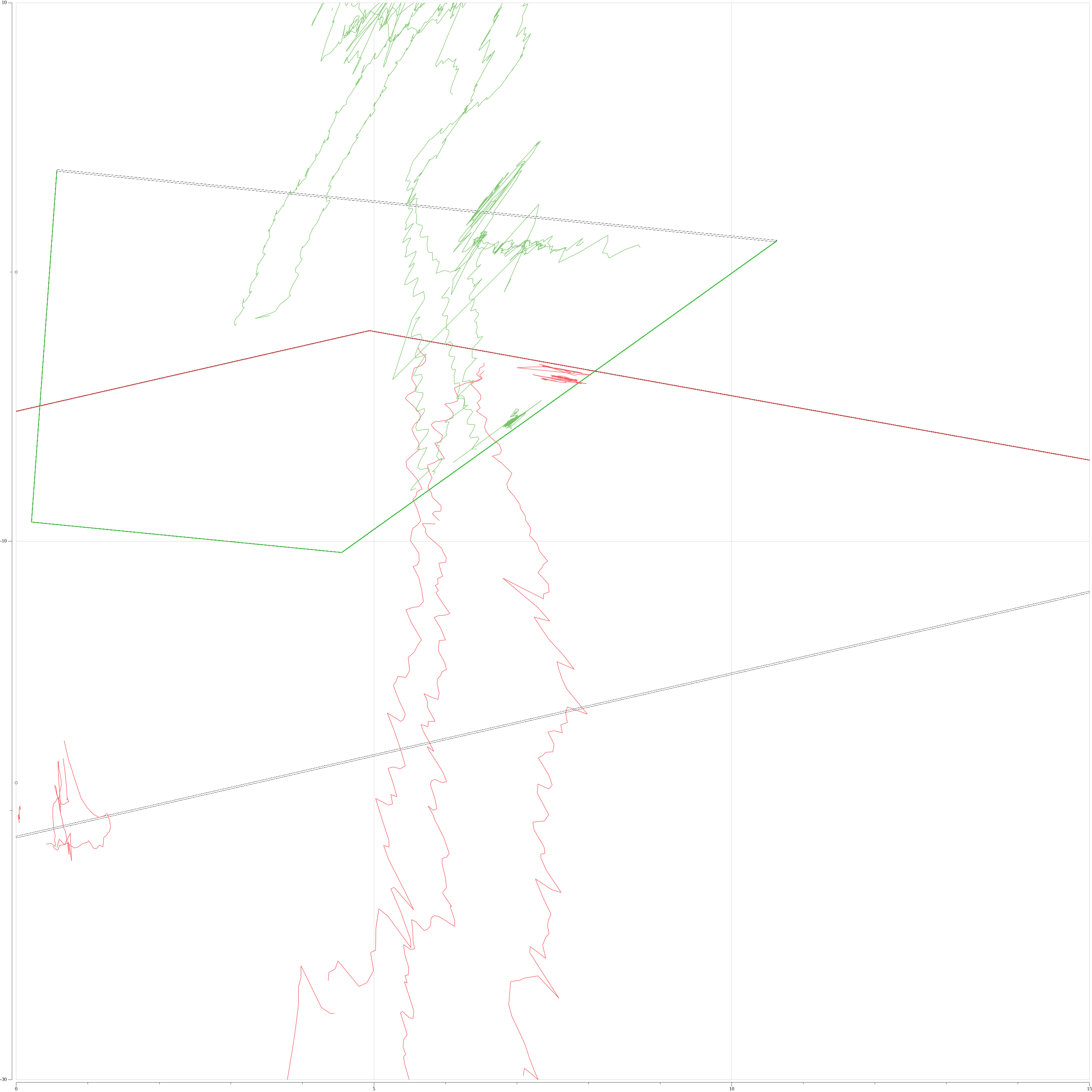
Fig. 4-2 同一人物判定アルゴリズムで合成された軌跡

2カメラの画角にまたがってプロットされている。

🐓 Results

本プロジェクトで得られた通行人の三次元座標を3DゲームエンジンのUnityで可視化し、視覚的な検証を行った。動画上側がカメラ1視点、下側がカメラ2視点である。

2カメラに同時に映る3人の歩行者全員の軌跡をUnity上の画面(右側)で追跡できているのがわかる。

🍗 Conclusion

本システムの実現性

Resultsでの視覚的な検証結果から言えば、人流の把握という本プロジェクトの目的は達成できたといえる。

ただ、2カメラからの$\alpha$平面への投影が完全には被らなかったことを踏まえ、その原因と対策を次に挙げる。

カメラの光軸方向の傾き

水準器や傾斜センサーで光軸方向の傾きを測定する

地面の傾斜、歩行者の身長

今回は時間の都合上出来なかったが、既知の高さのものを映像に収めれば、より正確な仰角・方位角の推定が可能となる。同時刻の同一物への2カメラからの投影がほとんど一点で交わるようになれば歩行者の身長も推定できるかもしれない。

画角計算に用いた測定値の誤差

実際の運用ではカメラの内部データから正確な焦点距離や画角が取得可能

2カメラの時刻同期にずれ

配信される動画のメタ情報にNTPサーバーとの同期によって得られた正確な時刻を含めるのが有効だと思われる。

まとめると、実際の運用では

カメラのワールド座標を得るための測量を行えば十分な精度の人流追跡が可能。
より正確な三次元座標を得るには以下のことが必要。
- 光軸方向の傾斜の測量
- 既知の高さのものを2カメラに収める
- 2カメラの時刻の同期

本システムの有用性

つぎに、本システムで達成できるデータ量削減の効果を概算する。

2カメラで撮影した動画(30fps、HD解像度)をH.264コーデックでストレージサーバに転送した場合、通信帯域は300kbpsほどである。

😋 Discussion

今後の展望

MergeNetなどを用いた単眼カメラのデプス推定と組み合わせれば、カメラの外部パラメータを実測なしに推定することができるかもしれない
3D座標に圧縮した状態ではそれ以上の物体検出はできないので、直近のデータは従来通り動画形式で保存するハイブリッドな運用も考えられる。

👨🏻‍💻 Source Code

パラメータ推定と2D可視化に用いたGoコード

https://github.com/payashi/golang-videointelligence

3D可視化に用いたUnityのC#コード

using System.Collections;
using System.Collections.Generic;
using UnityEngine;
using System;
using System.IO;
using Newtonsoft.Json;
using Newtonsoft.Json.Converters;

public class TestScript: MonoBehaviour
{
  [SerializeField]
  // Prefab to replicate
  GameObject origin;
  // Each item corresponds to an entity detected in the videos
  List < Item > items = new List < Item > ();
  // Elapsed time since the video started
  private float timeElapsed;
  
  // Start is called before the first frame update
  void Start()
  {
    // Load json file
    string path = "Assets/Resources/iplots.json";
    StreamReader reader = new StreamReader(path);
    String json = reader.ReadToEnd();
    items.AddRange(JsonConvert.DeserializeObject < Item[] > (json));
    items = items.GetRange(0, 3);
    reader.Close();
    
    // Spawn objects out of camera view
    foreach(Item item in items)
    {
      float angle = Mathf.Atan2(
        item.plots[item.size - 1][1] - item.plots[0][1],
        item.plots[item.size - 1][0] - item.plots[0][0]
      ) * Mathf.Rad2Deg - 90;
      item.obj = Instantiate(
        origin,
        new Vector3(0.0 f, -2.0 f, 0.0 f),
        Quaternion.Euler(0, angle, 0)
      );
    }
  }
  
  // Update is called once per frame
  void Update()
  {
    timeElapsed += Time.deltaTime;
    // Pedestrian coordinates are taken every 100 ms
    int tidx = (int)(timeElapsed * 10);
    foreach(Item item in items)
    {
      if (tidx < item.start)
      {
        continue;
      }
      else if (tidx <= item.end)
      {
        int offset = tidx - item.start;
        // Unity's coordinate system is left-handed
        item.obj.transform.position = new Vector3(
          item.plots[offset][0],
          item.plots[offset][2],
          item.plots[offset][1]
        );
      }
      else if (item.end + 1 == tidx)
      {
        Destroy(item.obj);
      }
    }
  }
}

class Item
{
  public float loss;
  public int size;
  public int start, end;
  public float[][] plots;
  public GameObject obj;
}

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up